1.什么是AVL树

AVL树也叫二叉搜索平衡树
因为二叉搜索树如果插入顺序是有序的，那么这棵树的查找效率将会是O(N)，所以说在实际情况下，二叉搜索很少被使用
为了解决这个缺点，诞生了AVL树

左右子树都是AVL树，左右子树高度差绝对值（平衡因子值）不超过1（平衡因子值不一定是1，这只是一种实现方案）

一颗高度不平衡的树：

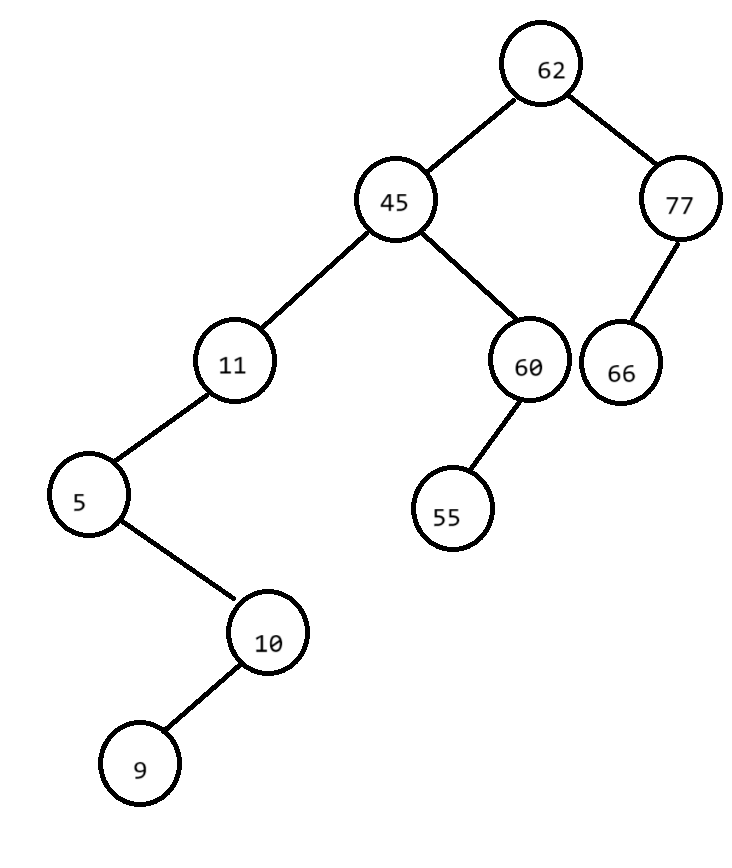
一颗AVL树：

一般的二叉搜索树在插入新节点以及删除节点时，都有可能会破坏树的平衡，所以AVL树需要对插入以及删除接口做修改，每次插入删除时，都要检测一下当前的树时候符合AVL树，如果不符合，要做出相应的调整措施
由于AVL树的这种特殊性质，使得它的查找效率是百分百的O(logn)

2.AVL树的实现

2.1节点类和基本结构

template<class K, class V>
struct AVLTreeNode //AVL树节点
{AVLTreeNode(const pair<K, V>& kv): _left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0){}//用三叉链,方便更新祖先的平衡因子AVLTreeNode<K,V>* _left;AVLTreeNode<K,V>* _right;AVLTreeNode<K,V>* _parent;pair<K, V> _kv;//存储的数据int _bf;//balance factor平衡因子
};

_left：指向左子树
_right：指向右子树
_parent：指向父节点
_bf：平衡因子
_kv：存储的键值对

template<class K,class V>
struct AVLTree //AVL树
{typedef AVLTreeNode<K, V> Node;
private:Node* _root;//定义一个根节点
};

2.2插入

插入有三个步骤：

1. 按照二叉搜索树规则插入节点
2. 插入完成后更新平衡因子
3. 若平衡因子不正确需要采取措施

更新平衡因子规则:

1. 新增在右，父亲的平衡因子_bf加一
   新增在左，父亲的平衡因子_bf减一
2. 更新完成后,父亲的_bf == 1 || -1，说明父亲插入前的_bf一定是0,插入后左右子树一边高一边低，需要继续向上更新平衡因子

3. 更新完成后父亲的bf==0，说明父亲在插入前的_bf是1/-1,并且插入后两边高度一致，不需要继续往上更新
   

4. 更新完成后父亲的_bf == 2 || -2，打破了平衡，父亲所在的子树要旋转处理
   

bool insert(const pair<K,V>& kv)//按照二叉搜索树的方式插入值
{if(_root == nullptr){_root = new Node(kv);return true; }Node* cur = _root;//要插入节点的位置Node* parent = nullptr;//其父亲的位置while(cur)//找到插入的位置{if(kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else if(kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else{return false;}}//找到了位置cur，开辟空间cur = new Node(kv);//父亲指向子if(kv.first > parent->_kv.first){	parent->_right = cur;}else{parent->_left = cur;}//子指向父cur->_parent = parent;//插入完成，检查平衡因子//沿插入位置cur向上更新平衡因子while(parent)//parent需要不断向上更新{	if(cur == parent->right){parent->_bf++;}else{parent->_bf--;}//不用向上更新if(parent->_bf == 0){	break;}//高度出现变化，向上更新平衡因子else if(parent->_bf == 1 || parent->_bf == -1){	parent = parent->parent;cur = cur->parent;}else if(parent->_bf == 2){//parent所在的子树不平衡了,需要旋转处理//后面会处理这处}}
}

2.3旋转处理

2.3.1左单旋

2.3.2右单旋

2.3.3左右双旋

2.3.4右左双旋

void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_+left;parent->_right = subRL;if(subRL){subRL->_parent = parent;}Node* parentparent = parent->_parent;subR->_left = parent;parent->_parent = subR;if(parent == _root){_root = subR;subR->_parent = nullptr;}else{if(parentparent->_left = parent){parentparent->_left = subR;}else{parentparent->_right = subR;}subR->_parent = parentparent;}subR->_bf = parent->_bf = 0;
}
void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (ppNode->_left == parent)ppNode->_left = subL;elseppNode->_right = subL;subL->_parent = ppNode;}subL->_bf = parent->_bf = 0;
}
void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);subLR->_bf = 0;if (bf == 1){parent->_bf = 0;subL->_bf = -1;}else if (bf == -1){parent->_bf = 1;subL->_bf = 0;}else if (bf == 0){parent->_bf = 0;subL->_bf = 0;}else assert(false);
}
void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);subRL->_bf = 0;if (bf == 1){subR->_bf = 0;parent->_bf = -1;}else if (bf == -1){subR->_bf = 1;parent->_bf = 0;}else if (bf == 0){parent->_bf = 0;subR->_bf = 0;}else assert(false);
}