源自：https://github.com/RAMshades/AcousticsM

特征提取

特征是可测量的属性，作为系统的输入。这些输入与特定数据样本相关，机器学习模型可通过解读这些特征来提供预测。特征通常具有独立性，并能提供样本的具体细节。音频特征示例包括（但不限于）：

• 音高
• 强度
• 能量
• 包络
• 音色
• 过零率
• 节奏
• 旋律
• 和弦

除上述特征外，还存在其他提取有效相关信息的方法。例如，可使用快速傅里叶变换或梅尔频率倒谱系数（下文将重点介绍）进行特征提取。

更广义而言，任何可作为输入的信息都可视为特征。这些特征类似于能引导我们得出词汇/解决方案/或任何有助于预测的描述要素。本笔记本将深入探讨维度令人困惑的特征提取世界及其重要性，主要涵盖以下主题：

1. 特征示例
2. 为何需要关注特征？
3. 特征提取方法示例
   • 一维特征提取
   • 二维特征提取
4. 参考文献

我们将在其他笔记本中讨论特征评估方法及如何选择最佳特征。

创建者：Ryan A. McCarthy

Import packages

# import packages
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from scipy import statsimport librosa 
import librosa.display
import IPython.display as ipdfrom glob import glob
import opendatasets as od 

特征示例

让我们看看Spotify热门歌曲提取的音频特征。

od.download('https://www.kaggle.com/datasets/julianoorlandi/spotify-top-songs-and-audio-features')
df = pd.read_csv("spotify-top-songs-and-audio-features/spotify_top_songs_audio_features.csv")
df

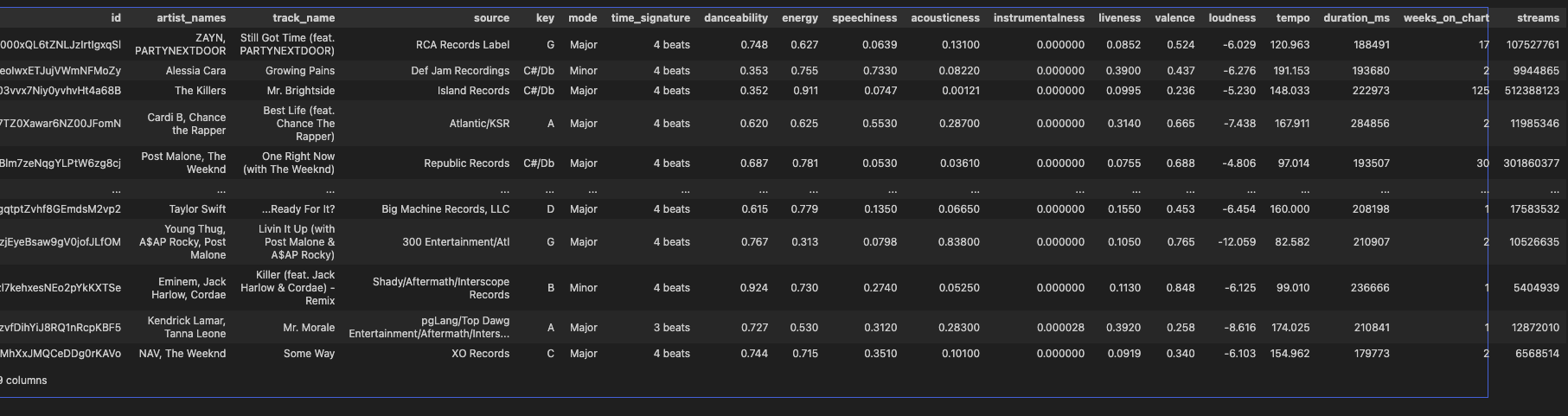
我们可以看到，这些特征可能包含数值型数据、分类型数据、布尔值等。需要注意的是，并非所有特征都有助于预测输出。某些特征可能会对模型造成干扰或存在模糊性。让我们以上述示例为基础，绘制特征间的相互关系图。这将帮助我们直观考察变量之间的协同变化情况。

# Plot
plt.figure(figsize=(10,8), dpi= 80)
sns.pairplot(df, kind="scatter", hue="key", plot_kws=dict(s=80, edgecolor="white", linewidth=2.5))
plt.title('Feature Comparisons')
plt.show()

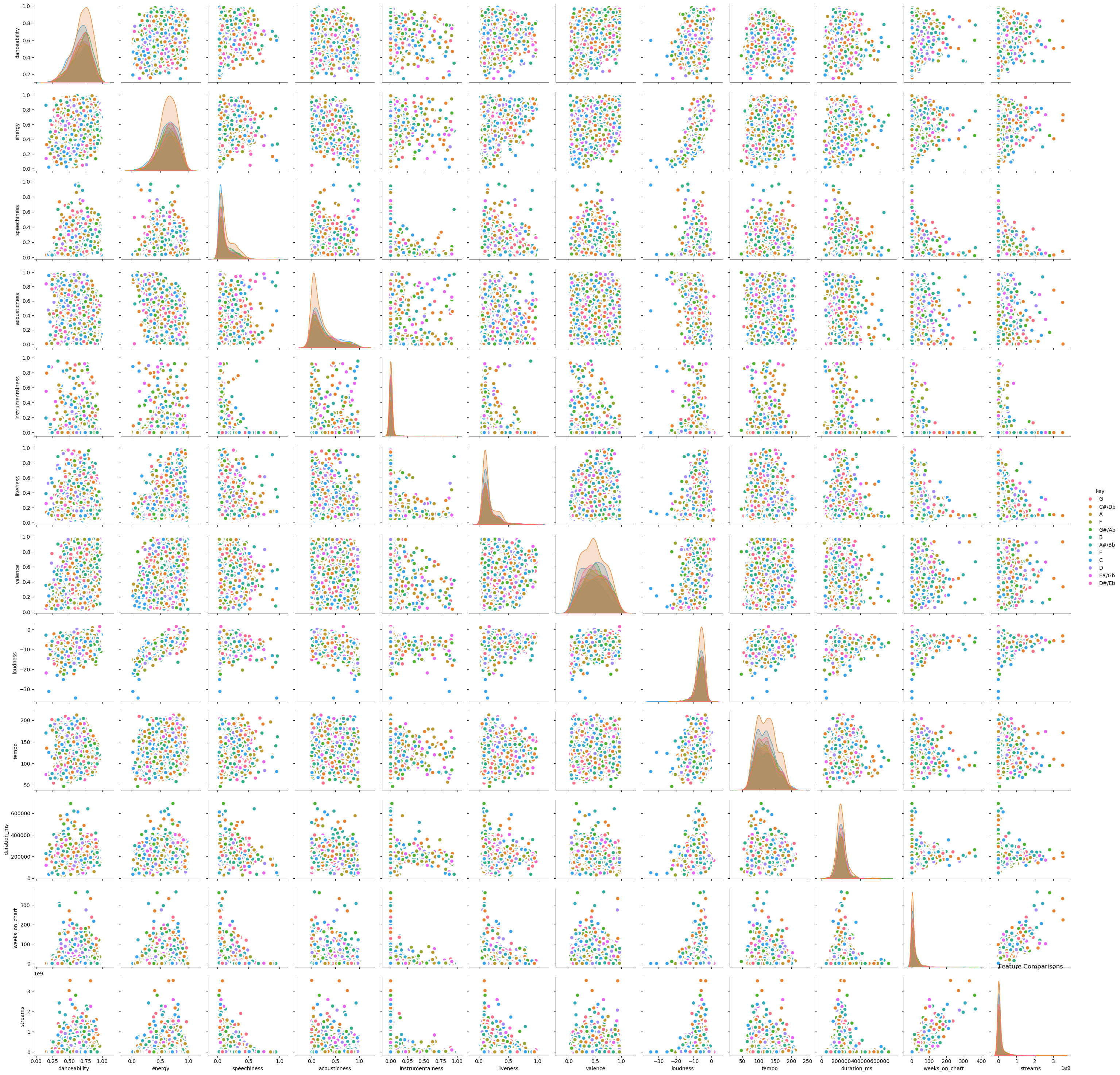
在许多情况下，我们希望移除线性相关的特征，因为它们无法提供显著独特的信息。然而，线性相关变量有时也可能具有价值，保留或移除这些特征的决定权在于机器学习模型的开发者。

为何需要关注特征？

特征选择对机器学习至关重要，错误的特征会导致模型预测出错误的分类或数值。此外，提供模糊信息可能产生误导性结果。例如，若我用毛发、耳朵、尾巴和两只眼睛来描述某个生物，很多人可能会认为我在描述猫或狗，但若缺乏更多信息则难以准确判断——这正是特征的作用所在：通过提供关键信息来消除模糊性，实现具体识别。

这种模糊性在声学机器学习中同样存在。使用特定频率的振幅等基础信息，可能有助于解决仅聚焦于该频率或特定场景的问题。例如在检测特定频率的蜂鸣声时，这种方法完全适用，因为只需关注该频率下的声音特征。但若需要识别具有相同频率的海豚咔嗒声与汽车鸣笛声，仅靠单一频率特征就显得不足。请注意，虽然存在大量特征与特征提取技术，但为简洁起见，下文仅重点介绍部分特征提取方法。

# Example Sound
filename = librosa.ex('trumpet')
y, sr = librosa.load(filename)# Play audio file
ipd.Audio(data=y,rate = sr)plt.figure(figsize = (8, 2))
librosa.display.waveshow(y = y, sr = sr);
plt.title("Sound Wave", fontsize = 23);
plt.ylabel('Amplitude')
plt.show()

一维特征

一维特征提取可包含从时间序列或信号中提取的数值型、分类型、时间序列等值。针对上述音频，我们将演示如何通过将数据分割成不同段落（具体采用2048个样本的窗口）来提取信息。这些方法可轻松应用于整个音频文件、半段音频或分段处理。

plt.figure(figsize = (8, 2))
librosa.display.waveshow(y = y, sr = sr);
for i in range(2048,len(y),2048):plt.axvline(x=i/sr,color='r')
plt.title("Sound Wave Split Up", fontsize = 23);
plt.ylabel('Amplitude')
plt.show()

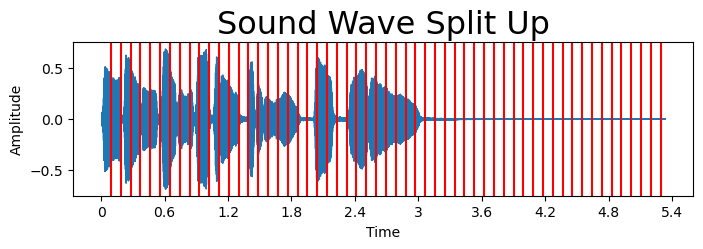
将数据分割成若干段落后，我们可以计算统计指标、通过一维卷积神经网络提取信息，或应用降维/扩维变换。

统计特征

统计特征可包含从数据中计算均值、方差、均方根、能量等指标。这些计算可作为特征提取的有效初步方法，因为（在许多情况下）机器学习模型需要借助数学规律来确定给定输入对应的输出概率。下文我们将探讨几种可提取的特征类型。

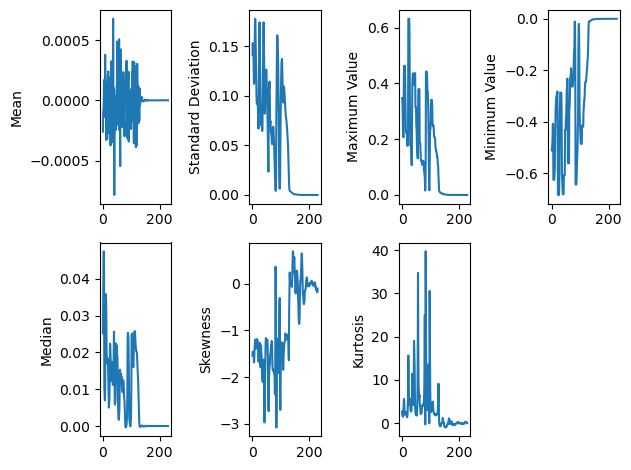
基础统计量

假设我们有一个长度为$n$（样本数量）的信号$x$，需要提取特征$A$。可采用的一种方法是计算信号平均值：
$$A\mu =\frac{{\sum }_{i=1}^n(x_i)}{n}.$$
信号平均值有助于提取潜在趋势并消除信号中的随机噪声，这对模型具有意义。在某些情况下，均值可能因受数据异常值影响过大而成为过于严苛的指标。此时可采用中位数计算：
$$A_{median}=\{\begin{array}{ll}\frac{x[\frac{n+1}{2}]}{x},& \text{若n为奇数}\\ \frac{x[\frac{n}{2}]+x[\frac{n}{2}+1]}{2},& \text{若n为偶数}\end{array}$$
中位数受异常数据影响较小，但预测效用可能相对有限。为考察信号变异程度，可提取标准差：
$$A\sigma =\sqrt{\frac{{\sum }_{i=1}^n(x_i-\mu {)}^2}{n}},$$
其中$\mu$是信号$x$的均值。标准差有助于理解信号的变异性。另一种特征提取方法是获取信号的最大值或最小值：
$$A_{max}=\max x:x=1,...,n,$$
$$A_{min}=\min x:x=1,...,n.$$
在基于振幅的分析中（例如判断声音是否超过阈值），最大值或最小值可能具有识别价值。对于后续两个特征，需要描述信号的矩。矩被定义为分布的定量特征，计算公式为：
$$m_r=\frac{1}{n}\sum _{i=1}^n(x_i-\mu {)}^r,$$
其中$r$为所计算的矩阶数[9]。若数据在均值附近存在偏斜（例如区分轻声音与响亮声音），可计算信号的偏度：
$$A_{偏度}=\frac{m_3}{m_2^{3/2}}$$
偏度可视为信号的第三标准化矩[9]。与此互补的峰度用于衡量信号分布的峰值特征：
$$A_{峰度}=\frac{m_4}{m_2^2}$$
峰度测量的是数据分布的第四中心矩[9]。

meanfeatures = []
stdfeatures = []
maxv = []
minv = []
median = []
skew = []
kurt = []
framelength = 2048
step = 512
for i in range(0,len(y),step):meanfeatures.append(np.mean(y[i:i+framelength]))stdfeatures.append(np.std(y[i:i+framelength]))maxv.append(np.max(y[i:i+framelength]))minv.append(np.min(y[i:i+framelength]))median.append(np.median(y[i:i+framelength]))skew.append(stats.skew(y[i:i+framelength]))kurt.append(stats.kurtosis(y[i:i+framelength]))plt.subplot(2,4,1)
plt.plot(meanfeatures)
plt.ylabel('Mean')plt.subplot(2,4,2)
plt.plot(stdfeatures)
plt.ylabel('Standard Deviation')plt.subplot(2,4,3)
plt.plot(maxv)
plt.ylabel('Maximum Value')plt.subplot(2,4,4)
plt.plot(minv)
plt.ylabel('Minimum Value')plt.subplot(2,4,5)
plt.plot(median)
plt.ylabel('Median')plt.subplot(2,4,6)
plt.plot(skew)
plt.ylabel('Skewness')plt.subplot(2,4,7)
plt.plot(kurt)
plt.ylabel('Kurtosis')plt.tight_layout()

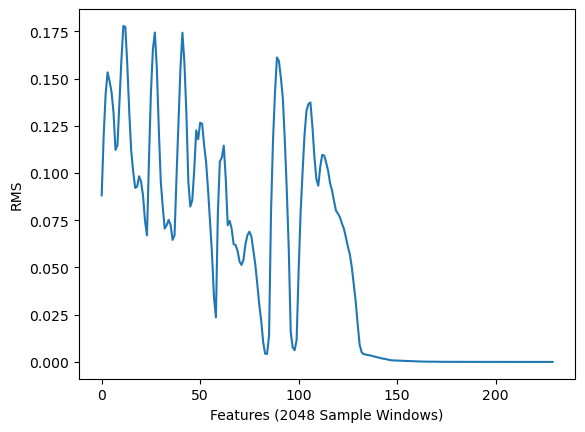
均方根

均方根（RMS）对应于信号的响度特性。长度为$n$（样本数量）的信号$x$的计算公式如下：

$$X_{rms}=\sqrt{\frac{x_1^2+x_2^2+...+x_n^2}{n}}.$$
均方根能够提供信号能量随时间波动的重要信息[10]。

# Loudness
rmsfeat = librosa.feature.rms(y=y,frame_length=2048)
plt.plot(rmsfeat[0])
plt.ylabel('RMS')
plt.xlabel('Features (2048 Sample Windows)')
plt.show()

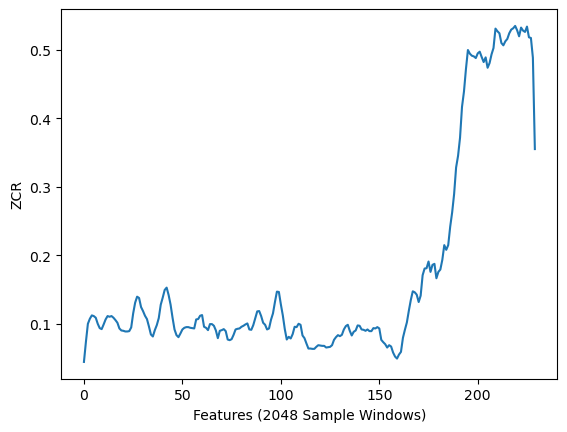
过零率

过零率（ZCR）定义为信号穿过零值的次数[11]。其计算公式如下：

$$zcr(A)=\frac{1}{2}\sum _{i=2}^n|sgn(x(i))-sgn(x(i-1))|,$$
其中$sgn$表示数字的符号函数。负数值返回$-1$，零值返回$0$，正数值则返回$1$。

# Zeros Crossing Rate
zcrfeat = librosa.feature.zero_crossing_rate(y=y,frame_length=2048)
plt.plot(zcrfeat[0])
plt.ylabel('ZCR')
plt.xlabel('Features (2048 Sample Windows)')
plt.show()

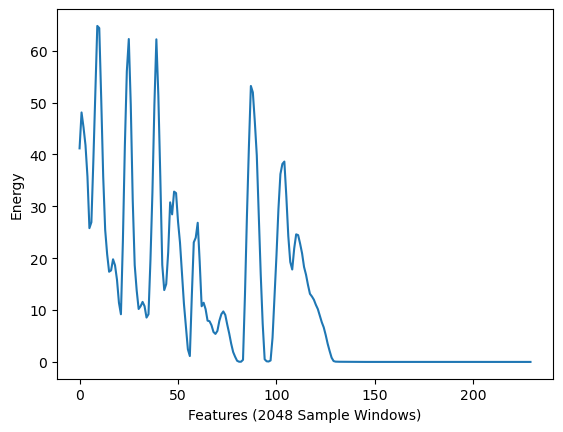
能量

信号的能量是指信号的总幅度，与信号的响度相关，其定义为：
$$E=\sum _{i=1}^n|x(i){|}^2.$$

# Energy of a signal
energy = []
framelength = 2048
step = 512
for i in range(0,len(y),step):energy.append(np.sum(y[i:i+framelength]**2))
plt.plot(energy)
plt.ylabel('Energy')
plt.xlabel('Features (2048 Sample Windows)')
plt.show()

变换方法

变换是一种通过缩减或扩展信号维度的方法，通过修改信号使其更适用于分析和模型训练。从统计学角度，变换可体现为对数、平方、指数等运算，这些运算将改变信号特性。另一种变换方法是通过卷积运算提取可用于模型训练的关键特征。下文我们将定义几种可实现信号扩展或缩减的变换方法。虽然未演示数据对数变换或平方变换的具体操作，但我们建议读者参阅文献[11]获取详细信息。

小波变换

小波是持续时间短、非对称且不规则的数学函数，能够将数据分解为不同频率和尺度分量[12]。虽然我们不会完整阐述小波理论，但建议读者参阅文献[12,13,14]。通常采用短时离散小波变换（DWT），通过一系列滤波器（如高通和低通滤波器）处理信号。

其数学表达式可写为：
$$T_{m,n}=a_0^{-m/2}\int x[t]\psi (a_0^{-m}[t]-n{b}_0)dt,$$
其中$\psi$为小波函数，$a$为伸缩参数，$b$为平移参数，$m$决定小波宽度（即高频或低频分量）。关于DWT的进一步说明可参阅文献[15]。小波变换具有多种应用场景，从数据压缩到特征提取均可适用。小波通过一族正交函数集来分解非周期连续函数。下文我们将使用PyWavelets包[6]演示小波变换及其不同函数族。

from scipy import signal
import pywt
pywt.families()

['haar','db','sym','coif','bior','rbio','dmey','gaus','mexh','morl','cgau','shan','fbsp','cmor']

哈尔小波

哈尔小波（以阿尔弗雷德·哈尔命名）的定义式为：
$${\psi }_{haar}(t)=\{\begin{array}{ll}1,& 0<t<\frac{1}{2}\\ -1,& \frac{1}{2}<t<1\\ 0,& \text{其他情况}\end{array}$$
这是一个在其支撑集上均值为零的分段常数函数。通过上述函数的伸缩和平移可构建标准正交基，其定义为：
$${\psi }_{j,n}(t)=\frac{1}{\sqrt{2^j}}\psi (\frac{t-2^{j}n}{2^j})$$
其中$(j,n)\in {\mathbb{Z}}^2$[14]。通过调整分解层级，可如下可视化哈尔小波的分解过程。

for n in range(1,4):plt.subplot(1,3,n)[phi, psi, x] = pywt.Wavelet('haar').wavefun(level=n**2)plt.plot(x,psi)plt.title(f'Level {n**2}')plt.ylim(-2,2)if n==1:plt.ylabel('Haar')
plt.tight_layout()
plt.show()

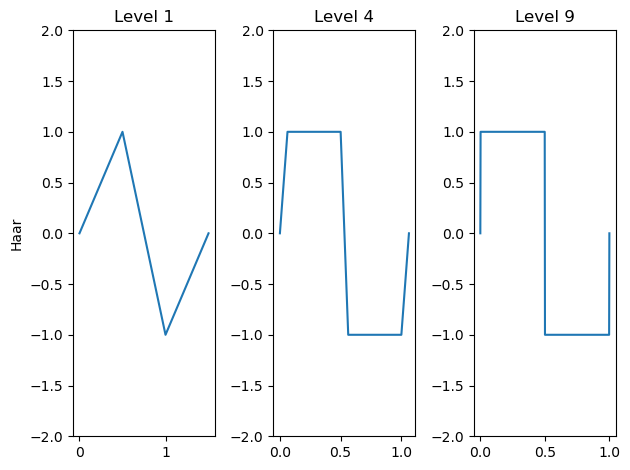
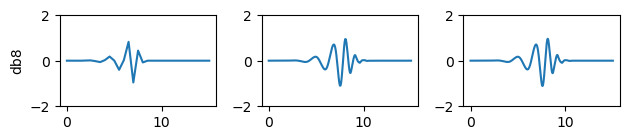
在上例中我们可以看到，使用的哈尔小波层级越高，小波就越趋于矩形波状形态。

道贝奇斯小波

道贝奇斯小波（以英格丽·道贝奇斯命名）以具有最多消失矩而著称。这类小波具有正交或双正交特性，且不具备对称性。其通常通过尺度函数表示为：
$$\psi (t)=\sqrt{2}\sum _{k=0}^{N-1}{c}_k\varphi (2t-k),$$
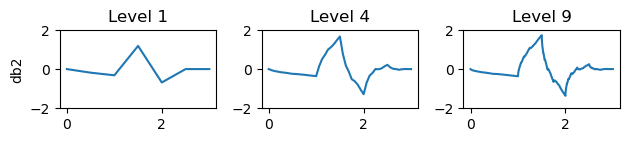
其中$\varphi$为尺度函数，N表示阶数[15]。下文我们将展示不同阶数和层级的道贝奇斯小波示例。

for n in range(1,4):plt.subplot(4,3,n)[phi, psi, x] = pywt.Wavelet('db2').wavefun(level=n**2)plt.plot(x,psi)plt.title(f'Level {n**2}')plt.ylim(-2,2)if n==1:plt.ylabel('db2')
plt.tight_layout()
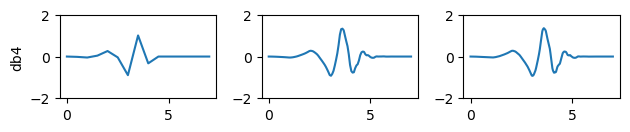
plt.show()for n in range(1,4):plt.subplot(4,3,n+3)[phi, psi, x] = pywt.Wavelet('db4').wavefun(level=n**2)plt.plot(x,psi)plt.ylim(-2,2)if n==1:plt.ylabel('db4')
plt.tight_layout()
plt.show()for n in range(1,4):plt.subplot(4,3,n+6)[phi, psi, x] = pywt.Wavelet('db6').wavefun(level=n**2)plt.plot(x,psi)plt.ylim(-2,2)if n==1:plt.ylabel('db6')
plt.tight_layout()
plt.show()for n in range(1,4):plt.subplot(4,3,n+9)[phi, psi, x] = pywt.Wavelet('db8').wavefun(level=n**2)plt.plot(x,psi)plt.ylim(-2,2)if n==1:plt.ylabel('db8')
plt.tight_layout()
plt.show()

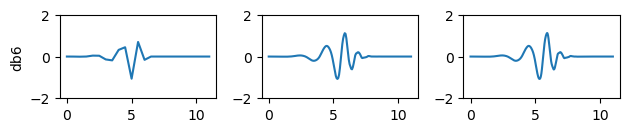
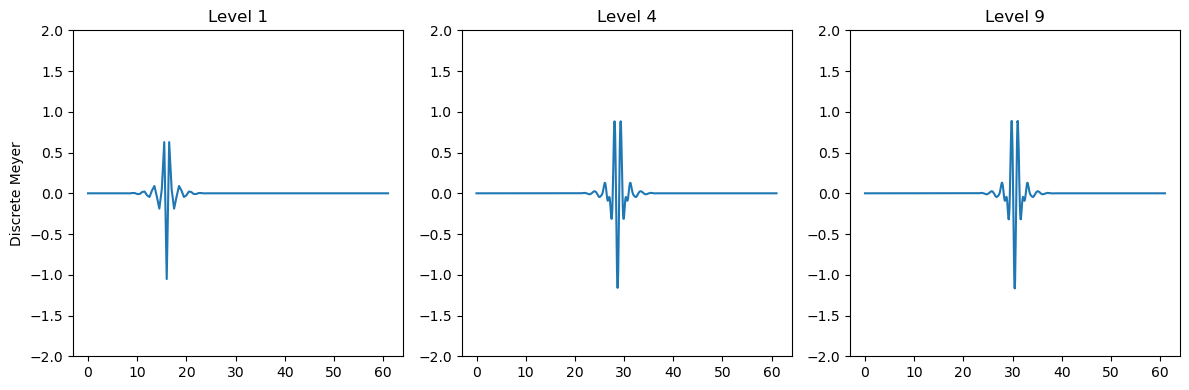
梅耶小波

梅耶小波（以伊夫·梅耶命名）是一种正交小波基，具有连续可微特性但不具备紧支撑性[16]。这类小波在频域中的定义为：
$${\psi }_{梅耶}(w)=\{\begin{array}{ll}\frac{1}{\sqrt{2\pi }}\cos (\frac{\pi }{2}V(\frac{3w}{2\pi }-1))e^{j\omega /2},& \text{若 }\frac{2\pi }{3}\le w\le \frac{4\pi }{3}\\ \frac{1}{\sqrt{2\pi }}\cos (\frac{\pi }{2}V(\frac{3w}{4\pi }-1))e^{j\omega /2},& \text{若 }\frac{4\pi }{3}\le w\le \frac{8\pi }{3}\\ 0,& \text{其他情况}\end{array}$$
其中V函数定义为：
$$V(x)=\{\begin{array}{ll}0,& \text{若 }x<0\\ x,& \text{若 }0<x<1\\ 1,& \text{若 }x>1\end{array}$$
梅耶小波具有如下所示的波形特征。

plt.figure(figsize=(12, 4))
for n in range(1,4):plt.subplot(1,3,n)[phi, psi, x] = pywt.Wavelet('dmey').wavefun(level=n**2)plt.plot(x,psi)plt.title(f'Level {n**2}')plt.ylim(-2,2)if n==1:plt.ylabel('Discrete Meyer')
plt.tight_layout()
plt.show()

小波在时间序列中的应用示例

在回顾上述几种小波族后，我们将探讨这些小波提取的信息特征，特别是近似系数与细节系数。近似系数对应信号的低频分量，类似于声音中的低频成分；反之，细节系数则对应信号的高频分量。这些系数（与母小波共同）有助于定义被分解的信号特征。下文将通过具体演示展现小波分解过程及其提取的近似系数与细节系数数值。

# Robin bird example
filename = librosa.ex('robin')
y, sr = librosa.load(filename)# Apply DWT
coeffs = pywt.dwt(y, 'db1')
cA, cD = coeffs# Plot the original signal and the approximation and detail coefficients
fig, axs = plt.subplots(len(coeffs) + 1, 1, figsize=(10, 8))
lim = np.max(abs(y))
axs[0].plot(y)
axs[0].set_title('Original Signal')
axs[0].set_ylim(-lim,lim)axs[1].plot(cA)
axs[1].set_title('Approximation (Level 1)')
axs[1].set_ylim(-lim,lim)axs[2].plot(cD)
axs[2].set_title('Coefficients (Level 1)')
axs[2].set_ylim(-lim,lim)plt.tight_layout()
plt.show()

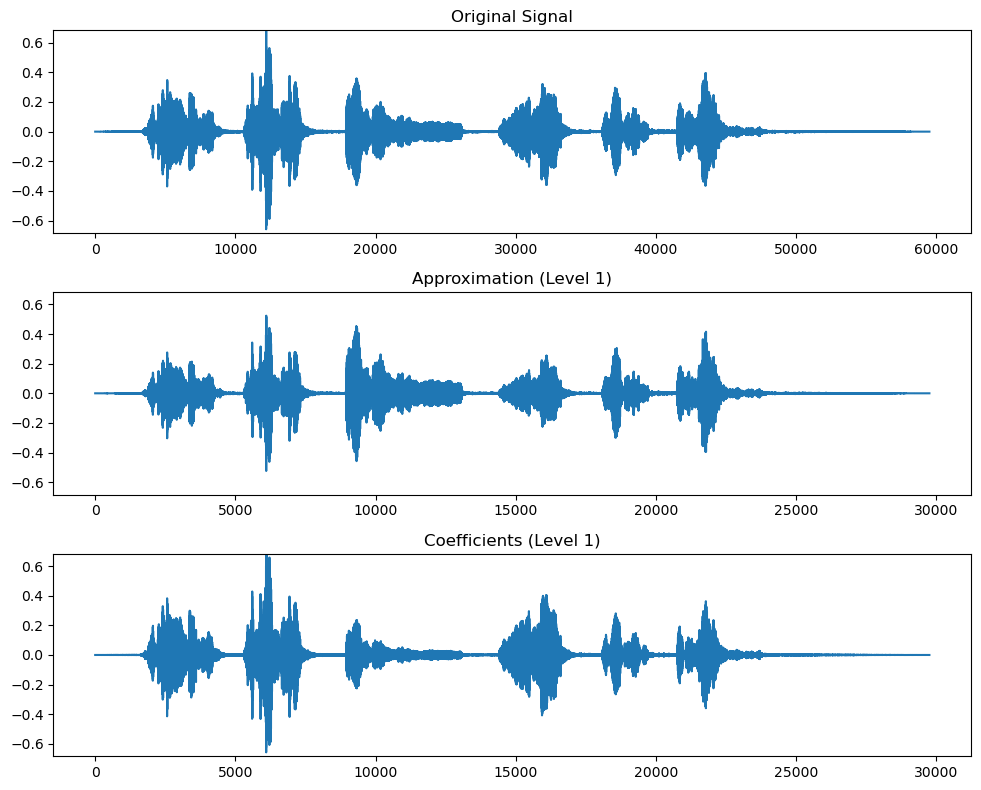
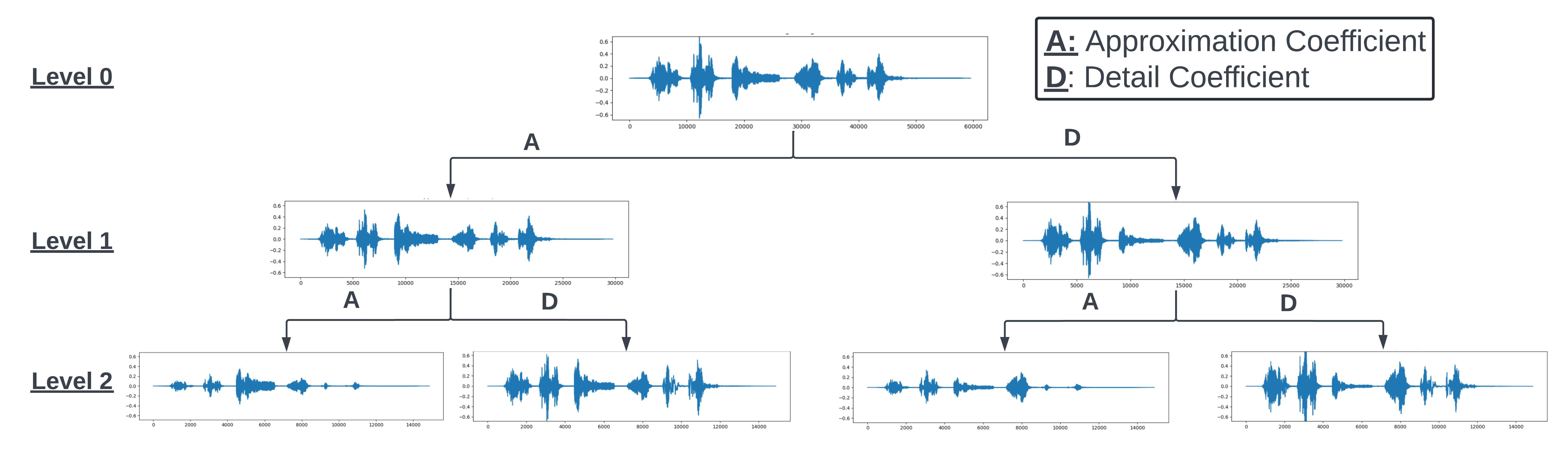
上例展示了使用小波变换后得到的近似系数与细节系数结果。这些输出值既可直接作为特征输入，也可用于进一步提取特征。需要特别注意的是，所得近似系数与细节系数的长度约为原始信号的一半——这与实施过程中对信号进行下采样的滤波处理有关。这些数值可按下图所示方式进行进一步分解。通过这种分层分解方式，可以在每个层级控制噪声和频率，从而实现在不同层级对信号进行处理。

from IPython.display import Image 
Image(url="Wavelet_decomp.jpeg", width=1500, height=1500) 

形状片段

形状片段转换算法（Shapelet Transform）从时间序列数据集中提取形状片段，并返回形状片段与时间序列之间的距离值。形状片段是指时间序列中连续时间点组成的子序列。为提升基于形状片段的分类效果，算法会筛选出最具判别性的形状片段。关于形状片段转换及其实现细节可参阅文献https://pyts.readthedocs.io/en/stable/auto_examples/transformation/plot_shapelet_transform.html，同时我们也提供了分割两种声学信号的示例以演示其工作原理。该算法从时间序列集合$T$中识别长度为$l$的候选序列：
Wl={W1,l∪...∪Wn,l}W_l = \{W_{1,l}\cup ... \cup W_{n,l}\} Wl​={W1,l​∪...∪Wn,l​}
其中n代表数据集中数据集的数量（即信号或音频记录的数量）。形状片段与长度为$l$的时间序列$T_i$子序列之间的最小距离定义为：
$$D_S=\min d(S,T_i^l)$$
式中d为距离计算公式（通常采用欧几里得距离）。算法通过该原理确定需要使用的显著形状片段。

from pyts.datasets import load_gunpoint
from pyts.transformation import ShapeletTransform# Toy dataset
X_train, _, y_train, _ = load_gunpoint(return_X_y=True)# Shapelet transformation
st = ShapeletTransform(window_sizes=[12, 24, 36, 48],random_state=42, sort=True)
X_new = st.fit_transform(X_train, y_train)# Visualize the four most discriminative shapelets
plt.figure(figsize=(6, 4))
for i, index in enumerate(st.indices_[:4]):idx, start, end = indexplt.plot(X_train[idx], color='C{}'.format(i),label='Sample {}'.format(idx))plt.plot(np.arange(start, end), X_train[idx, start:end],lw=5, color='C{}'.format(i))plt.xlabel('Time', fontsize=12)
plt.title('The four most discriminative shapelets', fontsize=14)
plt.legend(loc='best', fontsize=8)
plt.show()

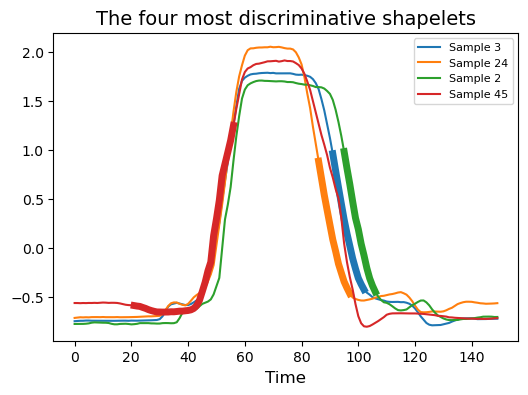
在上图中，我们可以看到四个最具区分度的形状片段，这些片段能够有效区分数据。通过计算时间序列与每个形状片段之间的距离，我们可以对数据进行转换，从而最终提升分类准确率。

使用两种声音的示例

假设我们有两种声音（小号与知更鸟鸣叫），需要找出这两种声学信号的区分特征。我们可以利用形状片段识别它们时间序列中的关键区段，从而实现分类与区分。

def split_array_equally(arr, n):"""Splits an array into equal parts and removes any unequal part."""size = len(arr) // nreturn [arr[i:i + size] for i in range(0, size * n, size)]# generate a dataset for classifciation based on examples
# trumpet example
filename = librosa.ex('trumpet')
y, sr = librosa.load(filename)data1 = np.vstack(split_array_equally(y,200)).T# Robin bird example
filename = librosa.ex('robin')
y, sr = librosa.load(filename)data2 = np.vstack(split_array_equally(y,200)).Tinputs = np.vstack([data1,data2])
outputs = np.vstack([np.ones((data1.shape[0],1)),2*np.ones((data2.shape[0],1))]).ravel()# Shapelet transformation
# transform the data using shapelets to 
st = ShapeletTransform(window_sizes=[12, 24, 36, 48],random_state=42, sort=True)
X_new = st.fit_transform(inputs,outputs)# Visualize the four most discriminative shapelets
plt.figure(figsize=(6, 4))
for i, index in enumerate(st.indices_[:4]):idx, start, end = indexplt.plot(inputs[idx], color='C{}'.format(i),label='Sample {}'.format(idx))plt.plot(np.arange(start, end), inputs[idx, start:end],lw=5, color='C{}'.format(i))plt.xlabel('Time', fontsize=12)
plt.title('The four most discriminative shapelets', fontsize=14)
plt.legend(loc='best', fontsize=8)
plt.show()

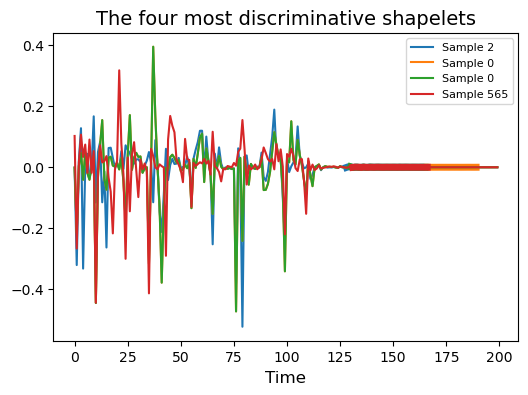
卷积核方法

随机卷积核变换（ROCKET）通过随机生成的卷积核进行特征提取，并为每个卷积核生成两个特征：最大值与正值比例[1]。ROCKET可通过两种方式运行：一是采用无监督技术，在不了解输出标签的情况下提取信息；二是采用有监督方法，识别能在数据中产生区分性的卷积核。下文我们以分段处理的小号与知更鸟鸣叫两种声音为例，演示ROCKET如何区分这两类声学片段。

from pyts.transformation import ROCKETdef split_array_equally(arr, n):"""Splits an array into equal parts and removes any unequal part."""size = len(arr) // nreturn [arr[i:i + size] for i in range(0, size * n, size)]# generate a dataset for classifciation based on examples
# trumpet example
filename = librosa.ex('trumpet')
y, sr = librosa.load(filename)data1 = np.vstack(split_array_equally(y,200)).T# Robin bird example
filename = librosa.ex('robin')
y, sr = librosa.load(filename)data2 = np.vstack(split_array_equally(y,200)).Tinputs = np.vstack([data1,data2])
outputs = np.vstack([np.ones((data1.shape[0],1)),2*np.ones((data2.shape[0],1))]).ravel()rocket = ROCKET(n_kernels=200, random_state=42)
x_rocket = rocket.fit_transform(X = inputs,y = outputs)# import PCA to decompose the data to plot
from sklearn.decomposition import PCApca = PCA(n_components=2)
X_r = pca.fit_transform(x_rocket)# Percentage of variance explained for each components
print("explained variance ratio (first two components): %s"% str(pca.explained_variance_ratio_)
)plt.figure()
target_name = ["trumpet","robin"]for i, target_name in zip([1, 2], target_names):plt.scatter(X_r[outputs == i, 0], X_r[outputs== i, 1], alpha=0.8, lw=lw, label=target_name)
plt.legend(loc="best", shadow=False, scatterpoints=1)
plt.title("PCA of ROCKET Transformed Data")plt.show()

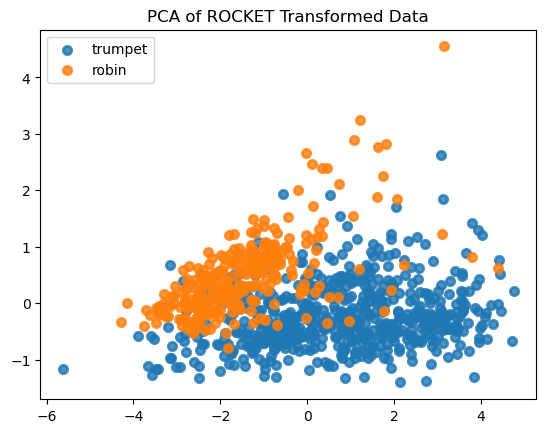
通过主成分分析结果可以看出，使用ROCKET变换后两类声音数据呈现出一定分离趋势，这种特征可用于训练预测模型。该方法虽然能快速获得结果，但难以解释从信号中提取的特征含义。

2D Features

频谱特征

让我们从一个简单的合成信号开始分析：

$$Y(t)=2\cos (f_{0}t)+4\sin (f_{1}t)+\cos (f_{2}t)+2\sin (f_{3}t)$$
其中$f_N$表示特定频率

# generate signal
sr = 25000x = np.arange(0,5,1/sr)f0 = 10
f1 = 10000
f2 = 5000
f3 = 2000
y = 2*np.sin(f0* 2*np.pi*x)+4*np.cos(f1* 2*np.pi*x)+.5*np.cos(f2* 2*np.pi*x)+3*np.cos(f3* 2*np.pi*x)plt.plot(x,y)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.show()

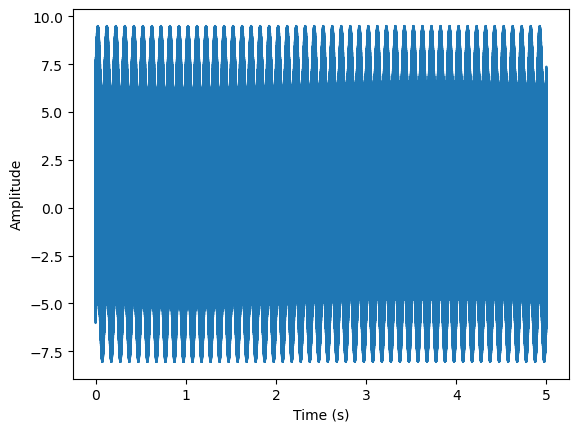
快速傅里叶变换与短时傅里叶变换

基于生成的信号，我们将计算单边快速傅里叶变换（FFT）与短时傅里叶变换（STFT）。首先简要定义FFT：给定长度为N的信号$x[n]$，其FFT计算公式定义为：
$$X[k]=\sum _{n=0}^{N-1}x[n]e^{\frac{-j2\pi kn}{N}}$$
其中k = 0,…,n-1 表示FFT的变换长度。这是FFT的离散形式。可以看出，该信号通过自然对数及其不同频率分量进行表征。

from scipy.fft import fft, fftfreq
N = len(x)
yf = fft(y)
xf = fftfreq(N, 1/sr)[:N//2]plt.plot(xf, 2.0/N * np.abs(yf[0:N//2]))
plt.grid()
plt.title('FFT')
plt.ylabel('Amplitude')
plt.xlabel('Hz')
plt.show()

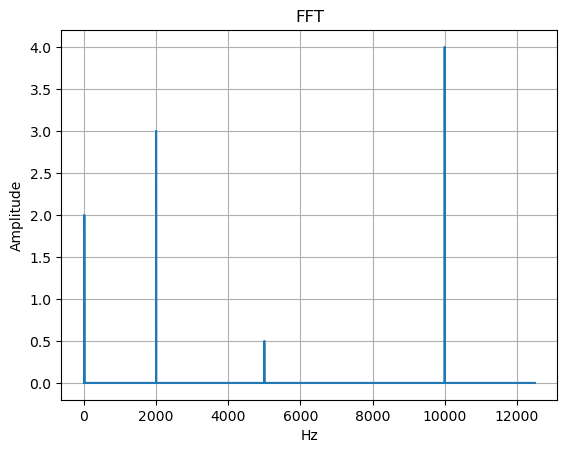
我们可以看到信号被分解为先前定义的频率分量。FFT的问题在于当信号中存在瞬态声音时，它无法捕捉局部瞬态特征且不包含任何时间分量。为解决这个问题，我们可以对信号进行分窗处理并应用FFT来捕捉瞬态声音，这种方法称为短时傅里叶变换（STFT）。下图展示了生成信号的STFT处理结果。

# Pre-compute a global reference power from the input spectrum
D = librosa.stft(y)  # STFT of y
S_db = librosa.amplitude_to_db(np.abs(D), ref=np.max)fig, ax = plt.subplots()
img = librosa.display.specshow(S_db, sr = sr,x_axis='time', y_axis='log', ax=ax)
ax.set(title='STFT')
fig.colorbar(img, ax=ax, format="%+2.f dB")
plt.show()

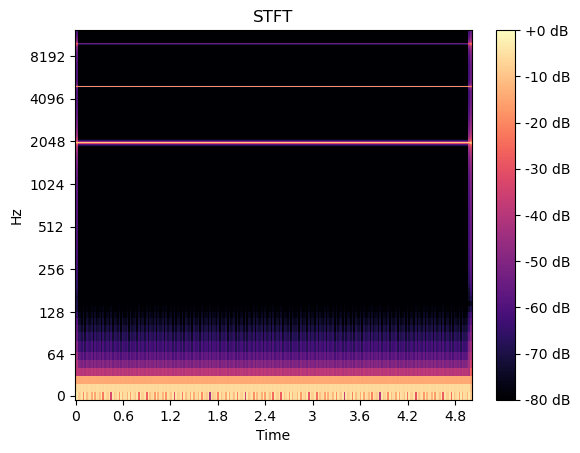
从上图可以清晰看到信号$y$中包含的频率成分及其对应的短时傅里叶变换结果。这类时频图像既可按频率/时间维度进行分解，也可输入大型卷积神经网络（CNN）中对STFT中呈现的声音特征进行分类。除短时频变换外，我们还可采用其他几种变换方法。

梅尔频谱图

另一种有效的二维表征方式是梅尔频谱图。其计算过程包括：对信号进行加窗处理，通过短时傅里叶变换（STFT）转换数据，使得到的频域表示通过梅尔滤波器组，最后对输出的频谱值进行求和与拼接。该滤波器组采用在梅尔刻度上等间隔排列的半重叠三角滤波器。更多技术细节可参阅https://ieeexplore.ieee.org/document/758101。

S = librosa.feature.melspectrogram(y=y, sr=sr, n_mels=128)fig, ax = plt.subplots()
S_dB = librosa.power_to_db(S, ref=np.max)
img = librosa.display.specshow(S_dB, x_axis='time',y_axis='mel', sr=sr, ax=ax)
fig.colorbar(img, ax=ax, format='%+2.0f dB')
ax.set(title='Mel-frequency spectrogram')
plt.show()

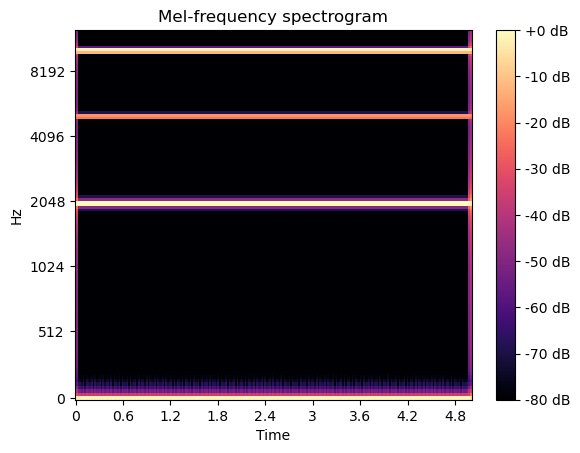
与短时傅里叶变换相似，梅尔频谱显示信号由频率成分构成，这些频率在频域上的分布范围略宽（即呈现更宽的频带）。

色谱图

还可采用其他表征方式，例如色谱图（chromagrams）——其将整个频谱映射到音高类别。每个八度音阶被划分为代表半音的音箱，这些八度音阶可用于区分音乐中的不同音高。

色谱图通过短时傅里叶变换计算波形或功率谱，该实现方法源自文献[7]。

filename = librosa.ex('trumpet')
y, sr = librosa.load(filename)# Chroma stft
S = librosa.feature.chroma_stft(y=y, sr=sr)fig, ax = plt.subplots()
S_dB = librosa.power_to_db(S, ref=np.max)
img = librosa.display.specshow(S_dB, y_axis='chroma', x_axis='time', sr=sr, ax=ax)
fig.colorbar(img, ax=ax, format='%+2.0f dB')
ax.set(title='Chroma STFT')
plt.show()

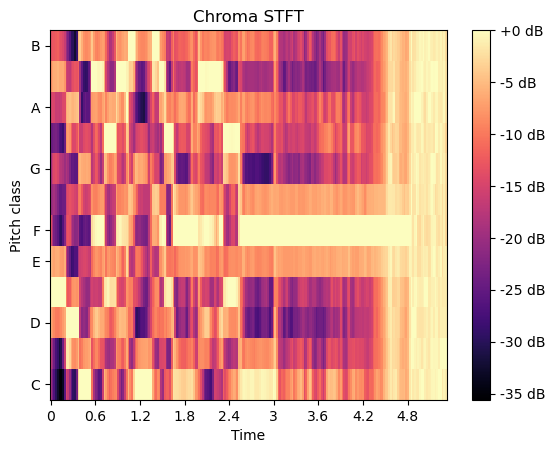
恒定Q值色谱图与傅里叶变换及莫雷小波变换相关，其采用在频率上按对数间隔排列的滤波器组实现。

# Chroma CQT
S = librosa.feature.chroma_cqt(y=y, sr=sr)fig, ax = plt.subplots()
S_dB = librosa.power_to_db(S, ref=np.max)
img = librosa.display.specshow(S_dB, y_axis='chroma', x_axis='time', sr=sr, ax=ax)
fig.colorbar(img, ax=ax, format='%+2.0f dB')
ax.set(title='Constant-Q Chromagram')
plt.show()

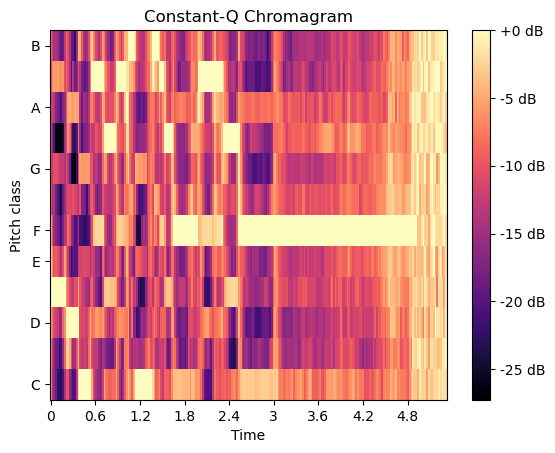
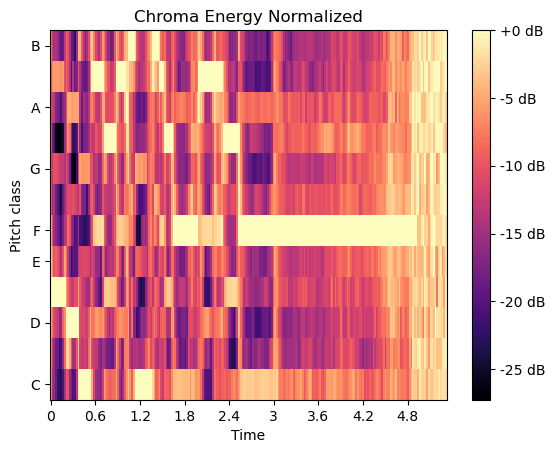
计算色谱变体“归一化色谱能量”（CENS）

计算CENS特征时，在通过chroma_cqt获取色谱向量后需执行以下步骤：

1. 对每个色谱向量进行L1归一化处理
2. 基于“类对数”幅度阈值对振幅进行量化

# Chorma CENS
chromagram = librosa.feature.chroma_cens(y=y, sr=sr)fig, ax = plt.subplots()
S_dB = librosa.power_to_db(S, ref=np.max)
img = librosa.display.specshow(S_dB, y_axis='chroma', x_axis='time', sr=sr, ax=ax)
fig.colorbar(img, ax=ax, format='%+2.0f dB')
ax.set(title='Chroma Energy Normalized')
plt.show()

References

1. A. Dempster, F. Petitjean and G. I. Webb, “ROCKET: Exceptionally fast and accurate time series classification using random convolutional kernels”. https://arxiv.org/abs/1910.13051.
2. J. Lines, L. M. Davis, J. Hills and A. Bagnall, “A Shapelet Transform for Time Series Classification”. Data Mining and Knowledge Discovery, 289-297 (2012).
3. Johann Faouzi and Hicham Janati. pyts: A python package for time series classification. Journal of Machine Learning Research, 21(46):1−6, 2020.
4. Scikit-learn: Machine Learning in Python, Pedregosa et al., JMLR 12, pp. 2825-2830, 2011.
5. McFee, Brian, Colin Raffel, Dawen Liang, Daniel PW Ellis, Matt McVicar, Eric Battenberg, and Oriol Nieto. “librosa: Audio and music signal analysis in python.” In Proceedings of the 14th python in science conference, pp. 18-25. 2015.
6. Gregory R. Lee, Ralf Gommers, Filip Wasilewski, Kai Wohlfahrt, Aaron O’Leary (2019). PyWavelets: A Python package for wavelet analysis. Journal of Open Source Software, 4(36), 1237, https://doi.org/10.21105/joss.01237.
7. Ellis, Daniel P.W. “Chroma feature analysis and synthesis” 2007/04/21 https://www.ee.columbia.edu/~dpwe/resources/matlab/chroma-ansyn/
8. Meinard Müller and Sebastian Ewert “Chroma Toolbox: MATLAB implementations for extracting variants of chroma-based audio features” In Proceedings of the International Conference on Music Information Retrieval (ISMIR), 2011.
9. Zwillinger, D. and Kokoska, S. (2000). CRC Standard Probability and Statistics Tables and Formulae. Chapman & Hall: New York. 2000.
10. D.I. Crecraft, S. Gergely, in Analog Electronics: Circuits, Systems and Signal Processing, 2002
11. Goswami, T., & Sinha, G. R. (Eds.). (2022). Statistical modeling in machine learning. San Diego, CA: Academic Press.
12. A. Graps, “An introduction to wavelets,” in IEEE Computational Science and Engineering, vol. 2, no. 2, pp. 50-61, Summer 1995, doi: 10.1109/99.388960.
13. T. Guo, T. Zhang, E. Lim, M. López-Benítez, F. Ma and L. Yu, “A Review of Wavelet Analysis and Its Applications: Challenges and Opportunities,” in IEEE Access, vol. 10, pp. 58869-58903, 2022, doi: 10.1109/ACCESS.2022.3179517.
14. Mallat Stéphane, (2009). In A Wavelet Tour of Signal Processing (p. iv). doi:10.1016/b978-0-12-374370-1.00001-x
15. Daubechies, I. Ten Lectures on Wavelets. CBMS-NSF Regional Conference Series in Applied Mathematics. Philadelphia, PA: Society for Industrial and Applied Mathematics, 1992.
16. I. Meyer, Wavelets and operators. Vol.1. Cambridge University Press, 1995.
17. Rabiner, Lawrence R., and Ronald W. Schafer. Theory and Applications of Digital Speech Processing. Upper Saddle River, NJ: Pearson, 2010.
18. S. Umesh, L. Cohen and D. Nelson, “Fitting the Mel scale,” 1999 IEEE International Conference on Acoustics, Speech, and Signal Processing. Proceedings. ICASSP99 (Cat. No.99CH36258), Phoenix, AZ, USA, 1999, pp. 217-220 vol.1, doi: 10.1109/ICASSP.1999.758101.