前言:各位老铁好，在前面博客中，笔者分享了有关二叉树的博客，在那篇博客中，笔者讲到了完全二叉树的存储结构中有两种存储方式，一种是顺序存储，一种是链式存储，链式存储笔者已经带各位老铁实现过了，今天笔者要分享的是，完全二叉树的顺序存储之堆。

1.堆的定义

那么什么是堆呢？我们肯定知道堆是一个完全二叉树，但是堆还需要满足一个条件，那就是每一个父节点的值必须大于等于其所有子节点的值(大根堆)，又或者是每一个父节点的值小于等于其所有子节点的值(小根堆)。
堆的图示

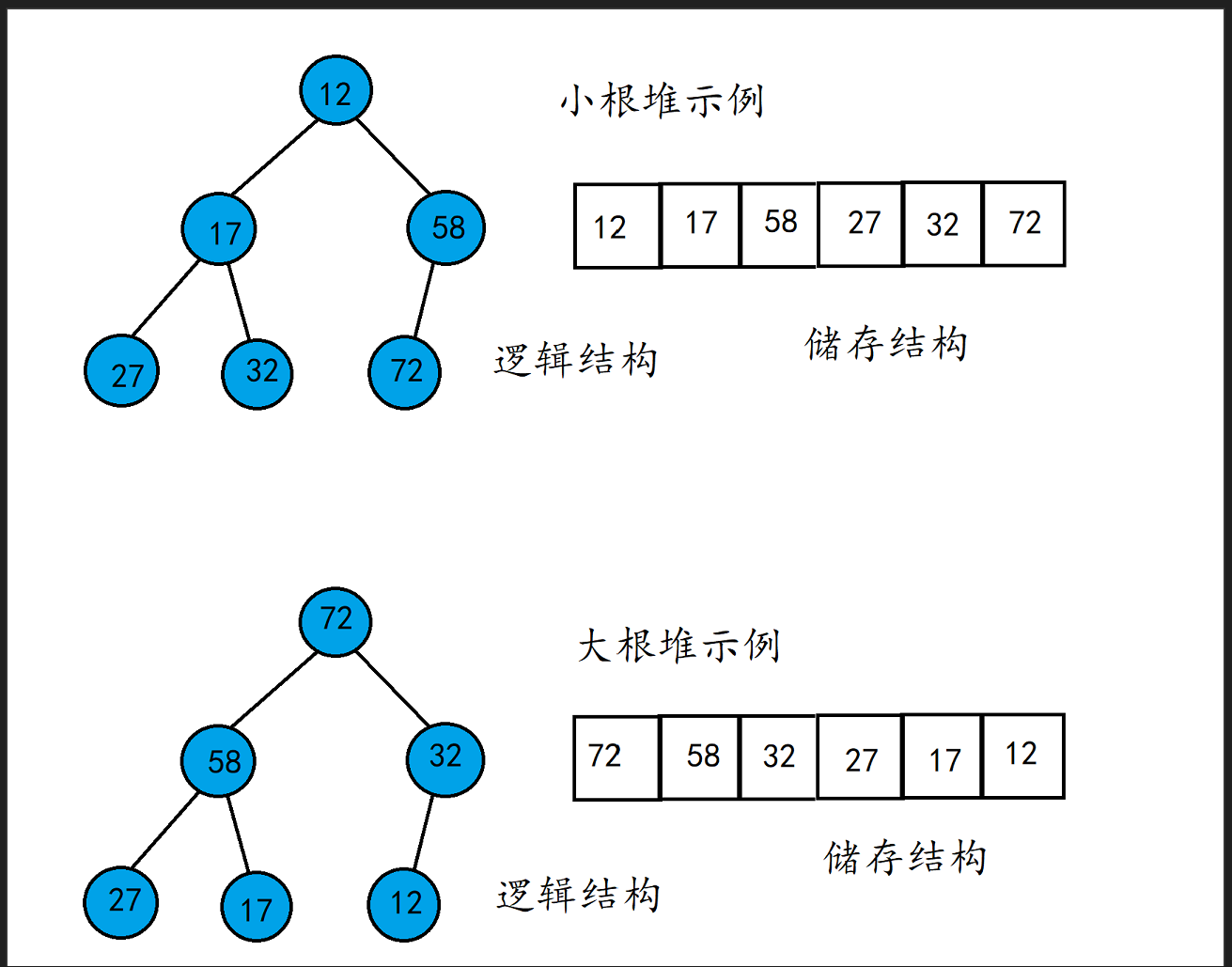
这里提一嘴，堆的实际的存储结构是数组来存储，我们一般把堆的逻辑结构看成是特殊的完全二叉树!!!

那么讲完了什么是堆，接下来就到堆实现的重头戏了。
再将堆结构的实现之前，我们先来铺垫两个概念
一个是向下调整算法，一个是向上调整算法

2.向下调整算法:向下调算法是有其中某一个非叶子节点不满足堆的性质，从而将它进行向下不断地调整到叶子节点，直到该节点满足堆地性质，向下调整算法有一个前提，该节点地左右子树必须满足堆的性质

可能有老铁看完笔者文字描述向下调整算法，对向下调整算法还不清楚，没关系，笔者接下来会举例加画图来给各位老铁讲解。

基于上面的内容，相信各位老铁一定懂得了向下调整算法了，那么接下来我们就需要来实现出向下调整算法，毕竟光说不练那是假把式嘛!(这里实现的是小根堆的向下调整算法)
我们知道堆的实际存储结构是数组，那么我们需要给堆传入一个数组，还需要有一个非叶子节点，因为我们是对非叶子节点进行调整嘛。(现在假设这个节点是根节点)
先定义一个结构体来表示堆(c语言实现，默认堆存储的整形数据)

#include <stdio.h>
typedef struct Heap
{int* _data;//存放数据int _size;//堆里面元素个数int _capacity;//整个空间大小
}Heap;

那么接下来就是实现向下调整算法了

typedef struct Heap
{int* _data;//存放数据int _size;//堆里面元素个数int _capacity;//整个空间大小
}Heap;//交换两个节点值
void Swap(int* h1, int* h2)
{int tmp=0;tmp = *h1;*h1 = *h2;*h2 = tmp;
}//n表示堆元素个数
void AdjustDowns(int* a, int n, int root)
{int parent = root;int child = parent * 2 + 1;while (child < n)//只要chlid节点还在堆范围内,就继续判断{//将parent节点和左右子节点进行比较if (child + 1 < n && a[child + 1] < a[child])//右子节点小于左子节点就++chlid{++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);//交换两个节点//更新chlid和parentparent = child;child = parent * 2 + 1;}//比父节点大不需要交换else{break;}}
}

3.向上调整算法:从某个节点开始，不断与父节点比较和交换，直到该节点满足堆的性质或者到达根节点为止，也需要满足除了这个节点的位置，前面的位置已经构成堆了。

笔者认为这个文字描述老铁们应该能看的懂了，所以笔者就不再画图了。
直接来实现向上调整算法了

//向上调整算法
void AdjustUp(int* a, int child)
{//先算出parent节点位置int parent = (child - 1) / 2;//减一是节点下标从0开始while (child > 0)//若该节点不是根节点就继续调整{if (a[child] < a[parent]){Swap(&a[child], &a[parent]);//更新child和parentchild = parent;parent = (child - 1) / 2;}else{break;}}
}

到这里我们就已经懂得了向上和向下调整算法了，下面我们就开始真正实现堆了。

4.初始化堆

void HeapInit(Heap* php)
{assert(php);//确保传入的对象不为空php->a = NULL;php->capacity = php->size = 0;
}

5.堆的插入

我们要明白堆的插入分为几种情况，是不是分为两种情况，一种是当存放数据的数组满了，是不是需要扩容才能插入，另一种是数组空间还足够，可以直接插入。

//堆的末尾插入数据
void HeapPush(Heap* php, int x)
{assert(php);//空间满了(按两倍来扩容)if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;int* tmp = (int*)realloc(php->a, sizeof(int) * newcapacity);if (tmp < 0){perror("realloc fail");//perror打印错误信息}php->a = tmp;php->capacity = newcapacity;}//插入数据php->a[php->size] = x;php->size++;//进行向上调整AdjustUp(php->a, php->size - 1);
}

6.取堆顶的数据

这个很简单，直接上代码了

int HeapTop(Heap* php)
{assert(php);assert(php->size);return php->a[0];
}

7.删除堆顶数据

如果我们直接删除堆顶的数据，是不是会破坏完全二叉树的结构，那么我们就换一种思路，通过将最后一个节点和第一个节点进行交换，然后在删除最后一个节点，最后再将第一个节点进行向下调整，这样就保持住了完全二叉树的结构。

void HeapPop(Heap* php)
{assert(php);assert(php->size > 0);//交换堆顶元素和最后一个元素Swap(&php->a[0], &php->a[php->size - 1]);//删除最后一个元素php->size--;//最后将第一个节点向下调整AdjustDown(php->a, php->size, 0);
}

8.判断堆是否为空

这个也很简单，直接上代码

bool HeapEmpty(Heap* php)
{assert(php);return php->size == 0;
}

9.释放堆

void HeapDestroy(Heap* php)
{assert(php);free(php->a);php->a = NULL;php->capacity = php->size = 0;
}

10.有关于堆常考的一个面试题:Topk问题

Topk问题:假设现在有n个数，需要让你选出最小的前k个数，你该如何选？

法一:使用堆排序，先建立一个大堆(建堆时间复杂度是0(n))，再让堆顶元素和最后一个元素进行交换，我们知道堆顶元素是当前的最大值，那么每一次交换到当前的最后一个元素，就确保了当前堆顶元素放到该放的位置，进行n-1次进行交换，那么就整个有序了，那么总的时间复杂度是o(n*logn)

法二:我们可以先建立有k个元素的最大堆(堆顶是当前k个元素中的最大值)，那么现在遍历剩下的n-k个元素，如果比堆顶元素小，那么就替换堆顶，然后再调整，直到替换出最小的前k个元素。

法三:假设现在n=10亿，我的内存肯定是存不下了，那么就不能直接使用堆排序了，那么这些值现在在文件中，那么我们该如何找出前k个最小元素

答:也是通过建立k个元素的大堆，再拿10亿-k的数据和堆顶数据比较，比堆顶小就替换堆顶并调整，最后一直比较完10亿-k个数据，就能找到最小的前k个元素了，那么我的内存仅仅需要维护o(k)