引言：当进化论遇见深度学习——自动化的黎明

在深度学习的蛮荒时代，我们是“手工匠人”。我们依靠直觉、前辈的经验（ResNet 为什么是152层而不是153层？）、大量的试错以及那么一点点玄学，在架构的黑暗森林中摸索前行。设计一个高性能的神经网络（Neural Network, NN），如同在中世纪手工锻造一把名剑，极度依赖铁匠（研究者/工程师）的个人技艺与运气。这个过程被戏称为“梯度下降炼丹术”，调的是超参数，炼的是时间和GPU资源。

但随着问题日益复杂，数据维度不断攀升，神经网络架构搜索（Neural Architecture Search, NAS） 应运而生，它预示着深度学习“工业革命”的到来。NAS的核心思想是：让算法自动地发现最优的网络架构，将人类从繁重重复的试错中解放出来。

在众多NAS方法中，基于进化计算（Evolutionary Computation），特别是遗传算法（Genetic Algorithm, GA） 的方法，因其强大的全局搜索能力、对问题域假设少以及天然的可并行性，占据了重要一席。它模拟了达尔文的自然选择理论：物竞天择，适者生存。让网络架构在代码的世界里“交配”、“变异”、“竞争”，一步步进化出最适应特定任务的“强者”。

本篇，我们将深入这场自动模型设计的进化之旅。我们将使用强大的进化算法库DEAP（Distributed Evolutionary Algorithms in Python），从零开始，构建一个属于我们自己的NAS系统，让遗传算法为我们自动设计卷积神经网络（CNN），并在经典数据集上验证其威力。

第一章：遗传算法（GA）—— 进化思想的数字涅槃

理论：生命游戏的代码镜像

遗传算法并非精确的数学求解器，而是一种受生物进化启发的元启发式（Meta-heuristic）优化算法。它的美妙之处在于，你不需要知道“最优解”长什么样，只需要定义一个方法来判断一个解（个体）的好坏（适应度），剩下的，交给进化。

其核心流程是一个精妙的循环，如下图所示，它完美复刻了自然选择的过程：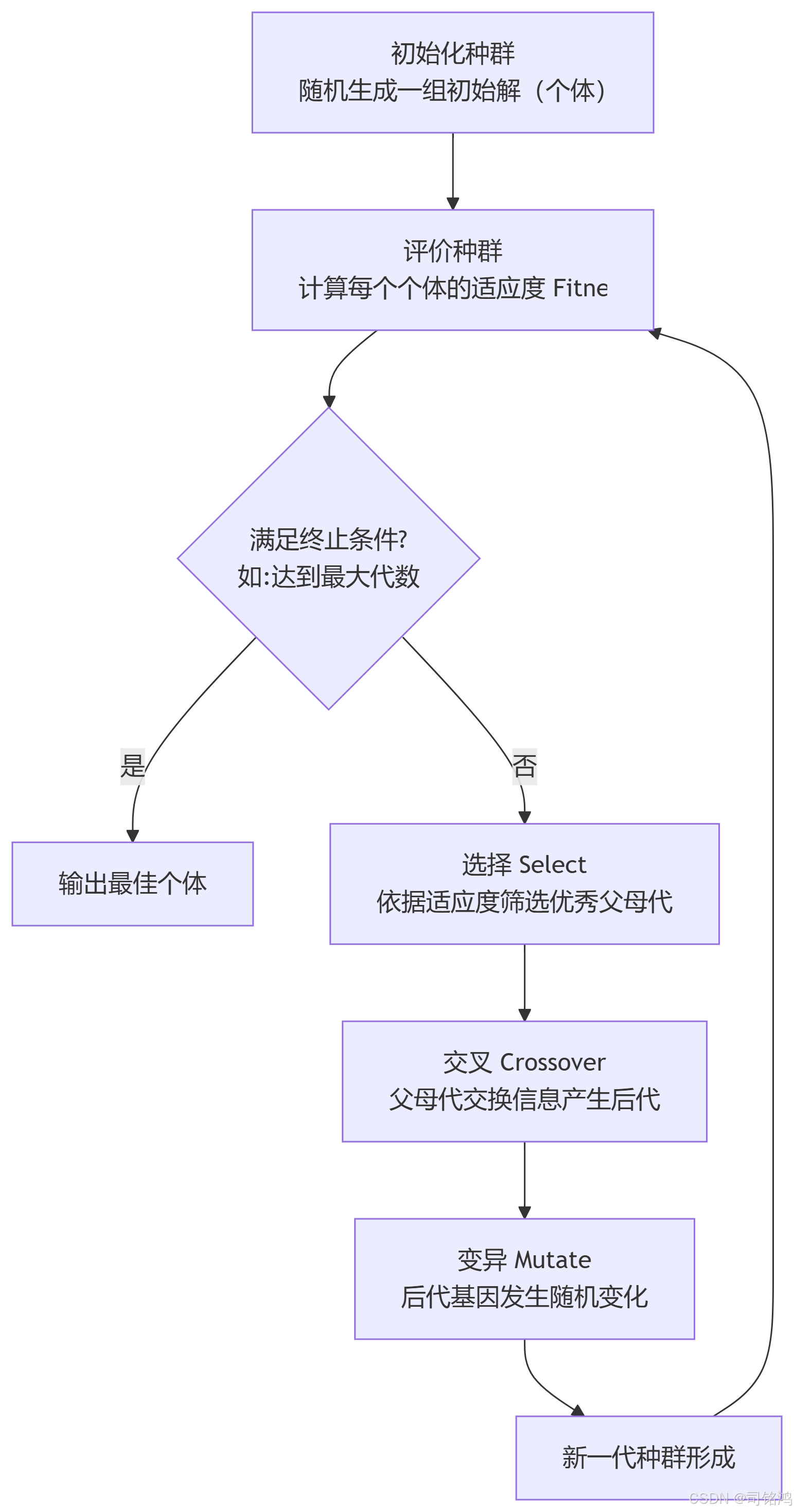

关键概念剖析：

个体（Individual）与种群（Population）：单个解称为一个个体（如：一个特定的网络架构配置）。所有个体的集合称为种群。在NAS中，一个个体就是一套完整的架构描述。
基因（Gene）与染色体（Chromosome）：描述个体特征的编码串称为染色体，其中的每一个单元称为基因。在NAS中，这可以是层类型、滤波器数量、连接方式等。
适应度（Fitness）：衡量个体优劣的数值。这是驱动整个进化过程的“上帝之手”。在NAS中，它通常是模型在验证集上的准确率（或准确率的函数）。
选择（Selection）：根据适应度概率性地选择优秀的个体作为父代，以产生后代。适应度越高，被选中的概率越大。常用策略有锦标赛选择（Tournament Selection）、轮盘赌选择（Roulette Wheel Selection）。
交叉（Crossover）：模仿有性繁殖的基因重组。随机选择两个父代个体，交换它们的一部分染色体，生成新的子代个体。这是探索解空间新区域的关键操作。
变异（Mutation）：以较低的概率随机改变个体中某个基因的值。它为种群注入新的多样性，避免算法过早陷入局部最优解。

实战：用DEAP实现一个简单的遗传算法

让我们先抛开神经网络，用DEAP解决一个经典问题：最大化一元函数 f(x) = x * sin(10π * x) + 1.0，其中 x 在区间 [-1, 2]。我们的目标是找到使得 f(x) 最大的 x。

步骤1：安装DEAP

pip install deap

步骤2：搭建进化流程

# 导入必要的库
import random  # 用于生成随机数
import numpy as np  # 用于数学计算
from deap import base, creator, tools, algorithms  # DEAP框架的主要模块# 定义问题类型：创建一个适应度类FitnessMax，用于最大化问题
# weights=(1.0,)表示单目标最大化问题，如果是多目标可以设置多个权重
creator.create("FitnessMax", base.Fitness, weights=(1.0,))# 创建个体类Individual，继承自list类型，并添加fitness属性
# 这样每个个体都是一个列表，同时具有适应度属性
creator.create("Individual", list, fitness=creator.FitnessMax)# 初始化工具箱，用于注册各种遗传算法操作
toolbox = base.Toolbox()# 注册基因生成器：定义一个名为attr_float的函数
# 该函数使用random.uniform生成[-1, 2)范围内的随机浮点数
toolbox.register("attr_float", random.uniform, -1, 2)# 注册个体生成器：定义一个名为individual的函数
# 使用initRepeat方法重复调用attr_float函数n次来创建个体
# 这里n=1表示每个个体只有一个基因（即x值）
toolbox.register("individual", tools.initRepeat, creator.Individual, toolbox.attr_float, n=1)# 注册种群生成器：定义一个名为population的函数
# 使用initRepeat方法重复调用individual函数来创建包含多个个体的种群
toolbox.register("population", tools.initRepeat, list, toolbox.individual)# 定义适应度函数（目标函数），用于评估个体的适应度
def eval_function(individual):# 从个体中提取x值（个体只有一个基因）x = individual[0]# 计算目标函数值：f(x) = x * sin(10π * x) + 1.0# 使用np.sin计算正弦值，10*np.pi*x是正弦函数的参数# 返回一个元组（因为DEAP要求适应度值以元组形式返回）return (x * np.sin(10 * np.pi * x) + 1.0),# 在工具箱中注册适应度评估函数
toolbox.register("evaluate", eval_function)# 注册交叉操作：使用混合交叉（模拟二进制交叉）
# alpha参数控制交叉的程度，0.5表示等比例混合
toolbox.register("mate", tools.cxBlend, alpha=0.5)# 注册变异操作：使用高斯变异
# mu=0表示变异的均值为0，sigma=0.2表示标准差为0.2
# indpb=0.2表示每个基因有20%的概率发生变异
toolbox.register("mutate", tools.mutGaussian, mu=0, sigma=0.2, indpb=0.2)# 注册选择操作：使用锦标赛选择
# tournsize=3表示每次锦标赛选择中随机选择3个个体进行比较
toolbox.register("select", tools.selTournament, tournsize=3)# 创建初始种群：生成包含50个个体的种群
pop = toolbox.population(n=50)# 定义统计指标，用于记录进化过程
# 使用Statistics对象收集进化过程中的统计信息
stats = tools.Statistics(lambda ind: ind.fitness.values)  # 提取个体的适应度值# 注册统计函数：计算适应度的平均值
stats.register("avg", np.mean)# 注册统计函数：计算适应度的标准差
stats.register("std", np.std)# 注册统计函数：找到适应度的最小值
stats.register("min", np.min)# 注册统计函数：找到适应度的最大值
stats.register("max", np.max)# 运行进化算法：使用eaSimple算法执行进化过程
# pop: 初始种群
# toolbox: 包含所有注册操作的工具箱
# cxpb=0.5: 交叉概率为50%
# mutpb=0.2: 变异概率为20%
# ngen=40: 进化40代
# stats: 统计对象，用于记录进化过程
# halloffame=None: 不保留名人堂（最优个体历史记录）
# verbose=True: 打印进化过程信息
pop, logbook = algorithms.eaSimple(pop, toolbox, cxpb=0.5, mutpb=0.2, ngen=40,stats=stats, halloffame=None, verbose=True)# 从最终种群中找到最佳个体：使用selBest函数选择适应度最高的个体
# k=1表示只选择最好的一个个体，[0]获取这个个体
best_individual = tools.selBest(pop, k=1)[0]# 获取最佳个体的适应度值
best_fitness = best_individual.fitness.values[0]# 打印最优解：格式化输出x值和对应的函数值
# :.6f表示保留6位小数
print(f"\n最优解: x = {best_individual[0]:.6f}, f(x) = {best_fitness:.6f}")

示例输出与解析：

gen     nevals  avg     std     min     max    
0       50      1.20518 0.511133 0.130204 1.85027
1       31      1.40997 0.305915 0.545786 1.85027
...
40      36      2.84977 0.012657 2.81321 2.85027最优解: x = 1.850547, f(x) = 2.850270

这个简单的例子展示了GA的核心框架。eaSimple 函数实现了完整的进化循环。我们可以看到，经过40代进化，种群的平均适应度和最大适应度都在稳步提升，最终找到了一个非常接近全局最优解（理论最大值在x≈1.85处）的结果。

第二章：神经网络架构的编码艺术——基因如何描述网络？

理论：从架构到染色体的映射

要让遗传算法为我们设计网络，首要任务是将抽象的神经网络架构（表现型, Phenotype）编码成一串数字（基因型, Genotype）。这是NAS中最关键也最具挑战性的一步。

常见的编码方式有：

直接编码（Direct Encoding）：显式地定义每一层的类型和参数。
- 示例基因：[('conv', 32, 3, 1), ('pool', 'max', 2), ('conv', 64, 3, 1), ...]
- 优点：直观，易于解码和理解。
- 缺点：染色体长度固定，限制了搜索空间的灵活性。
基于细胞的编码（Cell-based Encoding）：目前主流方法。先搜索一个或几种最优的细胞（Cell） 结构，然后通过堆叠重复的细胞来构建最终网络（如ResNet中的残差块，NASNet中的Normal Cell/Reduction Cell）。
- 优点：大大缩小了搜索空间，泛化能力强，易于迁移到不同规模的数据集。
- 缺点：编码和解码过程更复杂。

本节策略：为了清晰演示，我们采用一种简化的直接编码。我们固定网络的层数，但允许每一层的类型（卷积/全连接） 和超参数（滤波器数量/神经元数量） 变化。

我们的染色体将是一个列表，假设我们限定网络最多5层，每层有两种可能：

如果是卷积层（C），基因表示为 ('C', filters)
如果是全连接层（F），基因表示为 ('F', units)

例如，一个染色体 [('C', 64), ('C', 128), ('F', 256)] 代表一个3层网络：64滤波器的卷积层 -> 128滤波器的卷积层 -> 256个神经元的全连接层。

实战：定义架构的基因型与表现型转换

python

# 导入必要的库
import tensorflow as tf  # 导入TensorFlow深度学习框架
from tensorflow.keras.models import Sequential  # 导入Sequential模型类，用于按顺序堆叠层
from tensorflow.keras.layers import Conv2D, MaxPooling2D, Flatten, Dense, Dropout  # 导入各种神经网络层
from tensorflow.keras.optimizers import Adam  # 导入Adam优化器# 定义函数：将基因型（个体）解码为Keras模型（表现型）
# individual: 遗传算法中的个体，表示网络架构的基因编码
# input_shape: 输入数据的形状，例如(28, 28, 1)表示MNIST图像的尺寸
def create_network(individual, input_shape):"""将基因型（个体）解码为Keras模型（表现型）个体格式: [('C', 32), ('C', 64), ('F', 128), ...]其中'C'表示卷积层，后面的数字表示滤波器数量'F'表示全连接层，后面的数字表示神经元数量"""# 创建一个Sequential模型，这是一种按顺序堆叠层的线性模型model = Sequential()# 添加第一个卷积层：使用个体中的第一个基因来定义# individual[0][1]获取第一个元组的第二个元素，即滤波器数量# (3, 3)表示卷积核大小# activation='relu'使用ReLU激活函数# padding='same'表示使用相同填充，保持空间维度不变# input_shape指定输入数据的形状model.add(Conv2D(individual[0][1], (3, 3), activation='relu', padding='same', input_shape=input_shape))# 添加最大池化层，池化窗口大小为(2, 2)，用于降低特征图的空间维度model.add(MaxPooling2D((2, 2)))# 遍历个体中剩余的基因（从第二个开始）for layer_type, param in individual[1:]:# 如果基因类型是'C'（卷积层）if layer_type == 'C':# 添加卷积层，使用指定数量的滤波器和3x3卷积核model.add(Conv2D(param, (3, 3), activation='relu', padding='same'))# 添加最大池化层，进一步降低特征图维度model.add(MaxPooling2D((2, 2)))# 如果基因类型是'F'（全连接层）elif layer_type == 'F':# 在添加第一个全连接层之前，检查是否已经存在展平层# 使用any和isinstance检查模型中是否有Flatten层if not any(isinstance(layer, Flatten) for layer in model.layers):# 如果没有展平层，则添加一个展平层，将多维特征图转换为一维向量model.add(Flatten())# 添加全连接层，使用指定数量的神经元和ReLU激活函数model.add(Dense(param, activation='relu'))# 添加Dropout层，丢弃率为0.5，用于防止过拟合# Dropout在训练过程中随机丢弃一部分神经元，增强模型泛化能力model.add(Dropout(0.5))# 确保在输出层之前有展平层# 再次检查模型中是否有展平层，防止遗漏if not any(isinstance(layer, Flatten) for layer in model.layers):# 如果没有展平层，则添加一个model.add(Flatten())# 添加输出层：使用10个神经元，对应10个类别（假设是十分类任务）# 使用softmax激活函数，输出每个类别的概率分布model.add(Dense(10, activation='softmax'))# 返回构建好的模型return model# 示例：创建一个个体并解码为模型
# 定义一个示例个体，表示网络架构的基因编码
# [('C', 32)表示一个具有32个滤波器的卷积层
# ('C', 64)表示一个具有64个滤波器的卷积层
# ('F', 100)表示一个具有100个神经元的全连接层
example_individual = [('C', 32), ('C', 64), ('F', 100)]# 定义输入数据的形状，这里使用MNIST数据集的图像尺寸
# 28x28像素，1个颜色通道（灰度图像）
input_shape = (28, 28, 1)# 调用create_network函数，将基因型转换为表现型（Keras模型）
example_model = create_network(example_individual, input_shape)# 编译模型：配置模型的学习过程
# 使用Adam优化器，学习率设为0.001
# 使用稀疏分类交叉熵作为损失函数，适用于整数标签的分类问题
# 设置评估指标为准确率
example_model.compile(optimizer=Adam(learning_rate=0.001),loss='sparse_categorical_crossentropy',metrics=['accuracy'])# 打印模型的结构信息，包括每层的类型、输出形状和参数数量
example_model.summary()# 注意：在实际使用中，还需要准备训练数据和标签
# 例如：使用MNIST数据集
# (x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
# 然后对数据进行预处理（归一化、重塑形状等）
# 最后使用model.fit()方法训练模型

这个 create_network 函数就是我们连接遗传算法世界和深度学习世界的桥梁。它将一个编码好的染色体，实例化成了一个可以编译、训练、评估的Keras模型。

第三章：定义进化之力——适应度、交叉与变异

理论：NAS中的进化算子设计

在NAS的语境下，我们需要重新定义GA中的三个核心算子：

适应度函数（Fitness Function）：
- 任务：量化一个神经网络架构的好坏。
- 实现：通常是在一个验证集（Validation Set） 上计算准确率、F1分数等指标。为了节省计算资源，有时会使用低保真度评估（Low-Fidelity Evaluation），如在子数据集上训练、训练更少的轮数（Epoch）、使用权重共享等。
- 挑战：计算成本极高！评估一个个体可能需要几分钟到几小时。
交叉（Crossover）：
- 任务：交换两个父代架构（个体）的“优秀部件”以产生子代。
- 实现：对于直接编码，可以随机选择切点进行交换。例如，父代A [A1, A2, A3, A4] 和父代B [B1, B2, B3, B4] 在位置2交叉，产生子代 [A1, A2, B3, B4] 和 [B1, B2, A3, A4]。
变异（Mutation）：
- 任务：随机微调架构，引入多样性。
- 实现：以一定概率随机改变基因。例如：
  - 改变一层滤波器的数量（如从64变为128）。
  - 改变层的类型（如将卷积层变为全连接层，需注意维度兼容）。
  - 添加或删除一层（如果编码支持可变长度）。

实战：实现NAS的进化算子

# 导入必要的库
import random  # 用于生成随机数和随机选择
from deap import tools  # 导入DEAP框架的工具模块
import tensorflow as tf  # 导入TensorFlow深度学习框架
from tensorflow.keras.optimizers import Adam  # 导入Adam优化器
import gc  # 导入垃圾回收模块，用于释放内存# 假设已经定义了create_network函数和加载了MNIST数据
# 这里我们假设x_train, y_train, x_val, y_val已经定义# 1. 注册个体和种群创建方法（基于我们的编码）
# 定义网络层数，固定搜索5层网络
NUM_LAYERS = 5# 定义函数：随机生成一层网络结构
def random_layer():"""随机生成一层网络结构"""# 随机选择层类型：卷积层('C')或全连接层('F')layer_type = random.choice(['C', 'F'])# 根据层类型选择不同的参数范围if layer_type == 'C':# 卷积层的滤波器数量在[16, 32, 64, 128]中选择param = random.choice([16, 32, 64, 128])else:# 全连接层的神经元数量在[64, 128, 256, 512]中选择param = random.choice([64, 128, 256, 512])# 返回层类型和参数的元组return (layer_type, param)# 在工具箱中注册层生成器
# attr_layer函数使用random_layer生成随机层
toolbox.register("attr_layer", random_layer)# 注册个体生成器：使用initRepeat方法重复调用attr_layer函数NUM_LAYERS次
# 创建一个包含NUM_LAYERS个层的个体
toolbox.register("individual", tools.initRepeat, creator.Individual, toolbox.attr_layer, n=NUM_LAYERS)# 注册种群生成器：使用initRepeat方法重复调用individual函数创建多个个体
toolbox.register("population", tools.initRepeat, list, toolbox.individual)# 2. 定义适应度评估函数（这是最耗时的部分）
def evaluate_individual(individual):"""评估一个个体（网络架构）的适应度返回: (准确率, )"""# 设置训练参数以减少计算时间EPOCHS = 5  # 训练轮数，减少以加速搜索BATCH_SIZE = 256  # 批处理大小# 解码个体为Keras模型# 使用之前定义的create_network函数将基因型转换为表现型model = create_network(individual, (28, 28, 1))# 编译模型：配置优化器、损失函数和评估指标model.compile(optimizer=Adam(learning_rate=0.001),loss='sparse_categorical_crossentropy',metrics=['accuracy'])# 训练模型# 使用训练数据进行训练，验证集用于计算适应度# verbose=0表示不输出训练过程信息，减少输出干扰history = model.fit(x_train, y_train,batch_size=BATCH_SIZE,epochs=EPOCHS,validation_data=(x_val, y_val),verbose=0  # 不输出训练过程)# 取最后一个epoch的验证准确率作为适应度值# 使用验证集准确率而不是训练集准确率，以避免过拟合accuracy = history.history['val_accuracy'][-1]# 非常重要！清理模型和释放GPU内存# 删除模型引用del model# 清除Keras会话，释放GPU内存tf.keras.backend.clear_session()# 调用垃圾回收，确保内存被释放gc.collect()# 返回适应度值（准确率），注意返回元组格式return (accuracy, )# 在工具箱中注册评估函数
toolbox.register("evaluate", evaluate_individual)# 3. 定义交叉算子（单点交叉）
def crossover_individuals(ind1, ind2):"""对两个个体进行单点交叉"""# 确保个体长度相同，取较小长度size = min(len(ind1), len(ind2))# 随机选择交叉点（从1到size-1，确保不是端点）cxpoint = random.randint(1, size - 1)# 交换两个个体从交叉点到末尾的部分ind1[cxpoint:], ind2[cxpoint:] = ind2[cxpoint:], ind1[cxpoint:]# 返回交叉后的两个个体return ind1, ind2# 在工具箱中注册交叉操作
toolbox.register("mate", crossover_individuals)# 4. 定义变异算子
def mutate_individual(individual, indpb=0.2):"""以概率indpb变异个体的每一个基因"""# 遍历个体的每一个基因（层）for i in range(len(individual)):# 以indpb概率决定是否变异该基因if random.random() < indpb:# 如果决定变异，则用random_layer生成新的层替换原有层individual[i] = random_layer()# 返回变异后的个体（注意返回元组）return individual,# 在工具箱中注册变异操作，设置默认变异概率为0.2
toolbox.register("mutate", mutate_individual, indpb=0.2)# 5. 选择算子（沿用锦标赛选择）
# 注册选择操作：使用锦标赛选择， tournament大小为3
toolbox.register("select", tools.selTournament, tournsize=3)# 注意：在实际应用中，还需要定义进化算法的主循环
# 通常包括以下步骤：
# 1. 创建初始种群
# 2. 评估初始种群
# 3. 进行多代进化：
#     a. 选择父代
#     b. 应用交叉和变异产生子代
#     c. 评估子代
#     d. 选择下一代种群
# 4. 输出最优个体和其性能# 示例：创建和评估一个随机个体
if __name__ == "__main__":# 创建一个随机个体ind = toolbox.individual()print("随机个体:", ind)# 评估个体（需要确保MNIST数据已加载）# 注意：在实际运行前，需要先加载MNIST数据# (x_train, y_train), (x_val, y_val) = load_mnist_data()# fitness = evaluate_individual(ind)# print("个体适应度:", fitness)

关键点说明：

evaluate_individual 是性能瓶颈。这里我们只训练5个Epoch来粗略估计架构潜力，这是一种常见的加速策略。
每次评估后清理内存至关重要，否则长时间运行后内存/显存会耗尽。
交叉和变异操作要确保产生的个体是有效的（例如，全连接层之后可能不适合再接卷积层，我们的简单编码暂未处理此问题，更复杂的编码需要设计约束）。

第四章：运行进化NAS——释放算力，孕育架构

理论：并行进化与资源管理

现在，所有部件都已就位。但在按下“开始”按钮前，必须考虑两个现实问题：

并行计算（Parallelism）：评估成百上千个个体是令人尴尬的并行（Embarrassingly Parallel） 任务，因为每个个体的评估是独立的。DEAP支持多种并行后端（如multiprocessing）。
早停（Early Stopping）：如果某个架构在训练初期表现就极其糟糕，可以提前终止训练以节省资源。

实战：启动最终的架构搜索

我们将使用multiprocessing来并行评估个体，并运行完整进化流程。

# 导入必要的库
import multiprocessing  # 用于并行计算，加速适应度评估
import numpy as np  # 用于数学计算和统计
from deap import algorithms  # 导入DEAP的进化算法实现
import random  # 用于随机数生成
import tensorflow as tf  # 导入TensorFlow深度学习框架
from tensorflow.keras.optimizers import Adam  # 导入Adam优化器# 假设前面的代码已经定义了toolbox、create_network函数
# 以及加载了MNIST数据 (x_train, y_train, x_val, y_val, x_test, y_test)# 定义主函数，包含完整的神经架构搜索流程
def main():# 设置随机种子保证实验可重复性# 使用相同的种子可以复现实验结果random.seed(42)np.random.seed(42)# 设置TensorFlow的随机种子tf.random.set_seed(42)# 创建初始种群pop_size = 20  # 种群大小，即每代包含的个体数量pop = toolbox.population(n=pop_size)  # 使用工具箱创建初始种群# 设置并行评估，加速适应度计算# 使用多进程池，进程数为CPU核心数减1（保留一个核心给系统）pool = multiprocessing.Pool(processes=multiprocessing.cpu_count()-1)# 注册映射函数，使工具箱可以使用多进程并行评估个体toolbox.register("map", pool.map)# 定义统计和日志记录# 创建名人堂(HallOfFame)，保存历代最好的3个个体hof = tools.HallOfFame(3)# 创建统计对象，用于记录进化过程中的统计信息stats = tools.Statistics(lambda ind: ind.fitness.values)  # 提取个体的适应度值# 注册统计函数：计算适应度的平均值stats.register("avg", np.mean)# 注册统计函数：计算适应度的标准差stats.register("std", np.std)# 注册统计函数：找到适应度的最小值stats.register("min", np.min)# 注册统计函数：找到适应度的最大值stats.register("max", np.max)# 运行进化算法 (代数=10)# 使用eaSimple算法执行进化过程# pop: 初始种群# toolbox: 包含所有注册操作的工具箱# cxpb=0.7: 交叉概率为70%# mutpb=0.3: 变异概率为30%# ngen=10: 进化10代# stats: 统计对象，用于记录进化过程# halloffame: 名人堂对象，保存历代最优个体# verbose=True: 打印进化过程信息pop, logbook = algorithms.eaSimple(pop, toolbox, cxpb=0.7, mutpb=0.3, ngen=10,stats=stats, halloffame=hof, verbose=True)# 关闭并行池，释放资源pool.close()  # 阻止任何更多任务被提交到池pool.join()   # 等待所有工作进程退出# 输出最终结果print("\n=== 进化结束 ===")print("历代最佳个体 (Hall of Fame):")# 遍历名人堂中的所有个体for i, ind in enumerate(hof):# 打印每个个体的排名、基因型和适应度（验证准确率）print(f"Rank {i+1}: {ind}, Fitness (Val Accuracy): {ind.fitness.values[0]:.4f}")# 找到绝对最好的个体（名人堂中的第一个个体）best_individual = hof[0]print(f"\n*** 找到的最佳架构: {best_individual} ***")print(f"*** 其验证准确率: {best_individual.fitness.values[0]:.4f} ***")# 完整训练这个最佳架构并评估在测试集上的性能print("\n--- 开始完整训练最佳架构 ---")# 将最佳个体解码为Keras模型best_model = create_network(best_individual, (28, 28, 1))# 编译模型best_model.compile(optimizer=Adam(learning_rate=0.001),loss='sparse_categorical_crossentropy',metrics=['accuracy'])# 使用更多轮次（50轮）完整训练模型# 使用训练数据和验证数据，verbose=1显示训练进度history = best_model.fit(x_train, y_train,batch_size=256,epochs=50,validation_data=(x_val, y_val),verbose=1)# 在测试集上评估模型性能test_loss, test_acc = best_model.evaluate(x_test, y_test, verbose=0)print(f"\n!!! 最佳架构在测试集上的最终性能: {test_acc:.4f} !!!")# 返回种群、日志和名人堂，便于后续分析return pop, logbook, hof# 主程序入口
if __name__ == "__main__":# 确保在Windows下使用multiprocessing的正确方式# 在Windows上，多进程需要这个保护语句multiprocessing.freeze_support()# 调用主函数main()# 注意：在实际运行前，需要确保以下内容已定义或加载：
# 1. 工具箱(toolbox)的注册，包括个体创建、评估、交叉、变异和选择操作
# 2. create_network函数，用于将基因型转换为神经网络模型
# 3. MNIST数据集已加载并预处理为(x_train, y_train), (x_val, y_val), (x_test, y_test)
# 4. 可能需要调整一些参数，如种群大小、进化代数、训练轮数等，以适应具体硬件和时间限制# 运行过程解析：
# 程序会输出每一代的统计信息，包括最大适应度、平均适应度等
# 随着代数增加，通常会看到适应度逐渐提升的趋势
# 名人堂(HallOfFame)会保存历史上最好的3个架构
# 最终，程序会选出冠军架构，并用更多的训练轮次重新训练它
# 最后在测试集上评估性能，这是衡量NAS成功与否的最终标准

运行过程解析：
程序会输出每一代的统计信息。你会看到max（最佳适应度）和avg（平均适应度）随着代数增加而逐渐上升的趋势。HallOfFame对象会一直保存历史上最好的3个架构。最终，我们会选出冠军架构，并用更多的训练轮次（如50轮）重新训练它，并在从未见过的测试集上报告其最终性能。这才是衡量NAS成功与否的黄金标准。

第五章：超越与展望——NAS的前沿与挑战

我们的简单实验只是NAS世界的惊鸿一瞥。真正的工业级和研究级NAS要复杂得多：

更高效的搜索策略：
- 权重共享（Weight Sharing）：如ENAS。所有架构子模型在一个超网（Supernet）中共享权重，评估个体只需前向传播一次，极大加速适应度评估。
- 基于性能预测器（Performance Predictor）：训练一个回归模型，根据架构编码直接预测其性能，避免实际训练。
- 多目标优化：不仅优化精度，还同时优化参数量、FLOPs、延迟等（weights=(-1.0, 0.5) 表示最小化参数量，最大化精度）。
更复杂的搜索空间：
- 微分架构搜索（DARTS）：将离散的架构选择松弛为连续可微的优化问题，可用梯度下降高效求解。
- 层次化空间：同时搜索微观细胞结构和宏观网络骨架。
挑战：
- 计算成本：尽管有各种加速技术，搜索一个好的架构仍然需要巨大的算力。
- 可复现性：随机性的影响很大，两次搜索可能得到不同的结果。
- 泛化能力：在一个数据集上搜到的最优架构，能否很好地迁移到其他数据集？