电路特征介绍

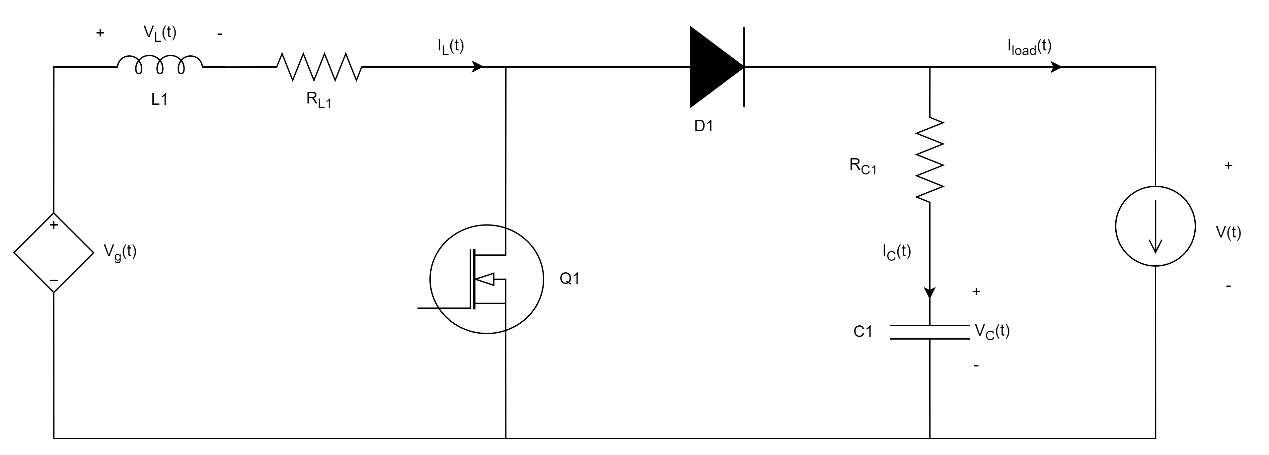
如图所示是一个非理想情况下的boost电路，其中 $L_{1}$ 和 $R_{L1}$ 是分别是电感和串联电阻； $C_{1}$ 和 $R_{C1}$ 是输出电容和串联电阻； $Q_{1}$ 是MOS管，其导通电阻是 $R_{on}$ ； $D_{1}$ 是二极管，正向导通电压是 $V_{f}$ ； $Vg(t)V_{g}\left. (t \right.)$ 是输入电压； $VL(t)V_{L}\left. (t \right.)$ 和 $IL(t)I_{L}\left. (t \right.)$ 分别是电感的电压和电流； $VC(t)V_{C}\left. (t \right.)$ 和 $IC(t)I_{C}\left. (t \right.)$ 分别是电容的电压和电流； $D(t)D\left. (t \right.)$ 表示占空比；T表示PWM开关周期； $V(t)V\left. (t \right.)$ 和 $Iload(t)I_{load}\left. (t \right.)$ 表示输出电压和输出电流，其他的符号说明如下：

$Vg(t)=VgV_{g}\left. (t \right.) = V_{g}$ + $v^g(t){\widehat{v}}_{g}\left. (t \right.)$ ， $IL(t)=IL+i^L(t)I_{L}\left. (t \right.) = I_{L} + {\widehat{i}}_{L}\left. (t \right.)$ ， $VC(t)=VC+v^c(t)V_{C}\left. (t \right.) = V_{C} + {\widehat{v}}_{c}\left. (t \right.)$ ， $V(t)=V+v^(t)V\left. (t \right.) = V + \widehat{v}\left. (t \right.)$ ， $Iload(t)=Iload+i^load(t)I_{load}\left. (t \right.) = I_{load} + {\widehat{i}}_{load}\left. (t \right.)$ ,
$D(t)=D+d^(t)D\left. (t \right.) = D + \widehat{d}\left. (t \right.)$ 。上式中前者表示直流量，后者表示扰动
$v^g(s){\widehat{v}}_{g}\left. (s \right.)$ ， $i^L(s){\widehat{i}}_{L}\left. (s \right.)$ ， $v^c(s){\widehat{v}}_{c}\left. (s \right.)$ ， $v^(s)\widehat{v}\left. (s \right.)$ ， $i^load(s){\widehat{i}}_{load}\left. (s \right.)$ ， $d^(s)\widehat{d}\left. (s \right.)$ 分别是 $v^g(t){\widehat{v}}_{g}\left. (t \right.)$ ， $i^L(t){\widehat{i}}_{L}\left. (t \right.)$ ， $v^c(t){\widehat{v}}_{c}\left. (t \right.)$ ， $v^(t)\widehat{v}\left. (t \right.)$ ， $i^load(t){\widehat{i}}_{load}\left. (t \right.)$ ， $d^(t)\widehat{d}\left. (t \right.)$ 的拉普拉斯变换

基于平均状态空间方程建模

在0~D(t)T期间，MOS管导通为一个电阻 $R_{on}$ ，二极管断开。

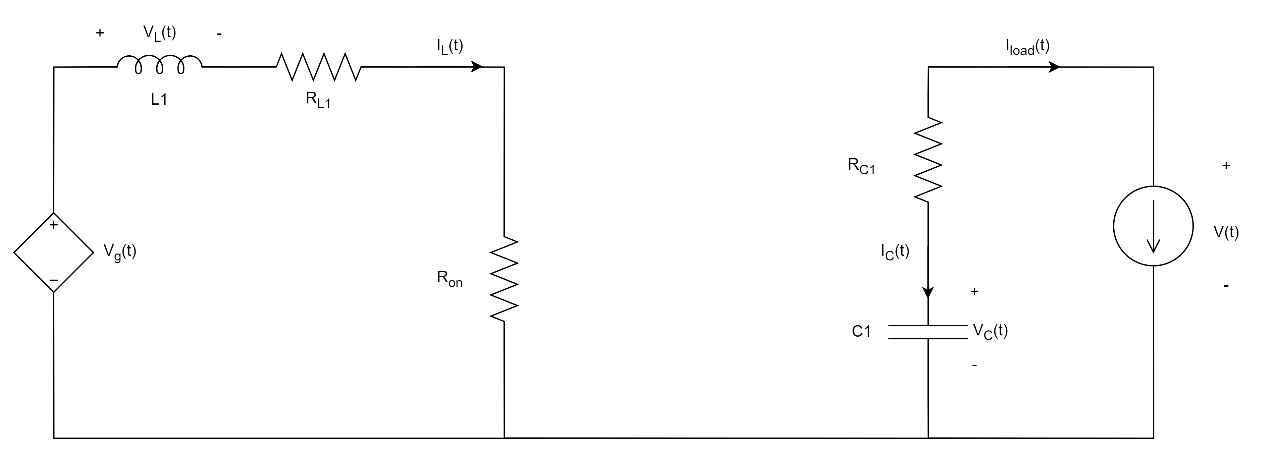
根据基尔霍夫电压(任何一个闭合回路的元件的电压降的代数和为0)和电流定律热(任意节点处各支路电流的代数和为0)，电感那一路顺时针压降应为0，顺着电流方向的电阻为降压，电容、电感、电压源等如果从正端口到负端口，电压降为负，反之为正，重点关注电感两端的感应电压和电感电流的极性，如上图所示：
$V_{g}(t) - V_{L}(t) - I_{L}(t)\left( R_{L1} + R_{on} \right) = V_{g}(t) - L_{1}\frac{dI_{L}(t)}{dt} - I_{L}(t)\left( R_{L1} + R_{on} \right)$

也可以进一步写成
$dIL(t)dt=Vg(t)−IL(t)(RL1+Ron)L1\frac{dI_{L}(t)}{dt} = \frac{V_{g}(t) - I_{L}(t)\left( R_{L1} + R_{on} \right)}{L_{1}}$

电容那一路的任意节点处的电流和应为0，可得
$I_{C}(t) + I_{load}\left. (t \right.) = C_{1}\frac{dV_{C}(t)}{dt} + I_{load}\left. (t \right.)$

也可以进一步写成
$dVC(t)dt=−Iload(t)C1\frac{dV_{C}(t)}{dt} = \frac{- I_{load}\left. (t \right.)}{C_{1}}$

电容那一路顺时针压降应为0
$V_{C}(t) + R_{C1}I_{C}(t) - V(t)\ = V_{C}(t) - R_{C1}I_{load}\left. (t \right.) - V(t)$

也可以进一步写成
$V(t) = V_{C}(t) - \ I_{load}R_{C1}\$

重新整理一下电感，电容和输出：
$dIL(t)dt=Vg(t)−IL(t)(RL1+Ron)L1dVC(t)dt=−Iload(t)C1{\frac{dI_{L}(t)}{dt} = \frac{V_{g}(t) - I_{L}(t)\left( R_{L1} + R_{on} \right)}{L_{1}} }{\frac{dV_{C}(t)}{dt} = \frac{- I_{load}\left. (t \right.)}{C_{1}}}$
${V(t) = V_{C}(t) - I_{load}R_{C1}}$

然后建立状态空间方程如下：
$ddt[IL(t)VC(t)]=[−(RL1+Ron)L1000][IL(t)VC(t)]+[1L1000−1C10][Vg(t)Iload(t)Vf]{\frac{d}{dt}\begin{bmatrix} I_{L}(t )\\ V_{C}(t ) \end{bmatrix} = \begin{bmatrix}-\frac{\left( R_{L1} + R_{on} \right)}{L_{1}} & 0 \\ 0 & 0 \end{bmatrix}\begin{bmatrix} I_{L}(t )\\ V_{C}(t) \end{bmatrix} + \begin{bmatrix} \frac{1}{L_{1}} & 0 & 0 \\ 0 & \frac{- 1}{C_{1}} & 0 \end{bmatrix}\begin{bmatrix} V_{g}\left. (t \right.) \\ I_{load}\left. (t \right.) \\ V_{f} \end{bmatrix}}$
$\begin{bmatrix} 0 & 1 \end{bmatrix}\begin{bmatrix} I_{L}(t) \\ V_{C}(t ) \end{bmatrix} + \begin{bmatrix} 0 & - R_{C1} & 0 \end{bmatrix}\begin{bmatrix} V_{g}(t) \\ I_{load}(t)\\ V_{f} \end{bmatrix}$

为了方便显示，将其改为下面的形式
$x(t)=[IL(t)VC(t)]x(t)=\begin{bmatrix} I_{L}(t ) \\ V_{C}(t) \end{bmatrix}$
$A1=[−(RL1+Ron)L1000]A_1 = \begin{bmatrix}-\frac{\left( R_{L1} + R_{on} \right)}{L_{1}} & 0 \\ 0 & 0 \end{bmatrix}$

$B_1 = \begin{bmatrix} \frac{1}{L_{1}} & 0 & 0 \\ 0 & \frac{- 1}{C_{1}} & 0 \end{bmatrix}$

$u(t)=[Vg(t)Iload(t)Vf]u(t)=\begin{bmatrix} V_{g}\left. (t \right.) \\ I_{load}\left. (t \right.) \\ V_{f} \end{bmatrix}$

$y (t) = V (t)$
$C_1 = \begin{bmatrix} 0 & 1 \end{bmatrix}$
$E_1 = \begin{bmatrix} 0 & - R_{C1} & 0 \end{bmatrix}$

也可以表示如下：
$dx(t)dt=A1x(t)+B1u(t){\frac{d\mathbf{x}(t)}{dt} = A_{1}\mathbf{x}(t) + B_{1}\mathbf{u}(t) }$
$y(t)=C1x(t)+E1u(t){\mathbf{y(t) =}\mathbf{C}_{\mathbf{1}}\mathbf{x(t) +}\mathbf{E}_{\mathbf{1}}\mathbf{u(t)}}$

对应的MATLAB脚本如下

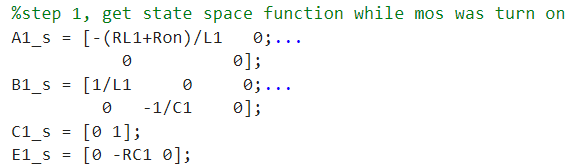
在D(t)T~T期间，MOS管断开，二极管导通为一个电压源 $V_{f}$

电容电流，电感电流以及输出电流应当满足
$IL(t)=IC(t)+Iload(t)=C1dVC(t)dt+Iload(t)I_{L}(t) = I_{C}\left. (t \right.) + I_{load}\left. (t \right.) = C_{1}\frac{dV_{C}(t)}{dt} + I_{load}\left. (t \right.)$

也可以进一步写成：
$IC(t)=IL(t)−Iload(t)dVC(t)dt=IL(t)−Iload(t)C1{I_{C}\left. (t \right.) = I_{L}(t) - I_{load}\left. (t \right.) }{\frac{dV_{C}(t)}{dt} = \frac{I_{L}(t) - I_{load}\left. (t \right.)}{C_{1}}}$

电感到电容这个环顺时针压降应为0，可得
$V_{g}(t) - V_{L}(t) - I_{L}(t)R_{L1} - V_{f} - I_{C}\left. (t \right.)R_{C1} - V_{C}\left. (t \right.) }{= V_{g}(t) - L_{1}\frac{dI_{L}(t)}{dt} - I_{L}(t)R_{L1} - V_{f} - \left( I_{L}(t) - I_{load}\left. (t \right.) \right)R_{C1} - V_{C}\left. (t \right.)}$

也可以进一步写成：
$dIL(t)dt=Vg(t)−IL(t)RL1−Vf−(IL(t)−Iload(t))RC1−VC(t)L1\frac{dI_{L}(t)}{dt} = \frac{V_{g}(t) - I_{L}(t)R_{L1} - V_{f} - \left( I_{L}(t) - I_{load}\left. (t \right.) \right)R_{C1} - V_{C}\left. (t \right.)}{L_{1}}$

电容和输出那一路顺时针压降应为0
$V_{C}(t) + I_{C}\left. (t \right.)R_{C1} - V(t) }{= V_{C}(t) + \left( I_{L}(t) - I_{load}\left. (t \right.) \right)R_{C1} - V(t)}$

也可以进一步写成：
$V_{C}(t) + \ \left( I_{L}(t) - I_{load}\left. (t \right.) \right)R_{C1}\$

重新整理一下电感，电容和输出：
$dIL(t)dt=Vg(t)−IL(t)(RL1+RC1)−Vf+Iload(t)RC1−VC(t)L1dVC(t)dt=IL(t)−Iload(t)C1V(t)=VC(t)+(IL(t)−Iload(t))RC1{\frac{dI_{L}(t)}{dt} = \frac{V_{g}(t) - I_{L}(t)\left( R_{L1} + R_{C1} \right) - V_{f} + I_{load}\left. (t \right.)R_{C1} - V_{C}\left. (t \right.)}{L_{1}} }{\frac{dV_{C}(t)}{dt} = \frac{I_{L}(t) - I_{load}\left. (t \right.)}{C_{1}} }{V(t) = V_{C}(t) + \left( I_{L}(t) - I_{load}\left. (t \right.) \right)R_{C1}}$

然后建立状态空间方程如下：
$ddt[IL(t)VC(t)]=[−(RL1+RC1)L1−1L11C10][IL(t)VC(t)]+[1L1RC1L1−1L10−1C10][Vg(t)Iload(t)Vf]\frac{d}{dt}\begin{bmatrix} I_{L}\left. (t \right.) \\ V_{C}\left. (t \right.) \end{bmatrix} = \begin{bmatrix}-\frac{\left( R_{L1} + R_{C1} \right)}{L_{1}} & \frac{- 1}{L_{1}} \\ \frac{1}{C_{1}} & 0 \end{bmatrix}\begin{bmatrix} I_{L}\left. (t \right.) \\ V_{C}\left. (t \right.) \end{bmatrix} + \begin{bmatrix} \frac{1}{L_{1}} & \frac{R_{C1}}{L_{1}} & \frac{- 1}{L_{1}} \\ 0 & \frac{- 1}{C_{1}} & 0 \end{bmatrix}\begin{bmatrix} V_{g}\left. (t \right.) \\ I_{load}\left. (t \right.) \\ V_{f} \end{bmatrix}$
$\begin{bmatrix} R_{C1} & 1 \end{bmatrix}\begin{bmatrix} I_{L}\left. (t \right.) \\ V_{C}\left. (t \right.) \end{bmatrix} + \begin{bmatrix} 0 & - R_{C1} & 0 \end{bmatrix}\begin{bmatrix} V_{g}\left. (t \right.) \\ I_{load}\left. (t \right.) \\ V_{f} \end{bmatrix}$

为了方便显示，将其改为下面的形式
$\begin{bmatrix} I_{L}(t ) \\ V_{C}(t) \end{bmatrix}$

${A}_{2}= \begin{bmatrix}-\frac{\left( R_{L1} + R_{C1} \right)}{L_{1}} & \frac{- 1}{L_{1}} \\ \frac{1}{C_{1}} & 0 \end{bmatrix}$

$B_2 = \begin{bmatrix} \frac{1}{L_{1}} & \frac{R_{C1}}{L_{1}} & \frac{- 1}{L_{1}} \\ 0 & \frac{- 1}{C_{1}} & 0 \end{bmatrix}$

$\begin{bmatrix} V_{g}\left. (t \right.) \\ I_{load}\left. (t \right.) \\ V_{f} \end{bmatrix}$

$y (t) = V (t)$

$C_2 = \begin{bmatrix} R_{C1} & 1 \end{bmatrix}$

$E_2 = \begin{bmatrix} 0 & - R_{C1} & 0 \end{bmatrix}$

也可以表示如下：
$u(t){\frac{d\mathbf{x(t)}}{dt} = \mathbf{A}_{\mathbf{2}}\mathbf{\ x(t) +}\mathbf{B}_{\mathbf{2}}\mathbf{\ u(t)}}$
$y(t)=C2x(t)+E2u(t){\mathbf{y(t) =}\mathbf{C}_{\mathbf{2}}\mathbf{x(t) +}\mathbf{E}_{\mathbf{2}}\mathbf{u(t)}}$

对应的MATLAB脚本如下

然后将0~DT期间和DT~T期间的状态空间方程矩阵按照权重D整合在一起，可得
$A=D(t)A1+(1−D(t))A2=D(t)[−(RL1+Ron)L1000]+(1−D(t))[−(RL1+RC1)L1−1L11C10]\mathbf{A = D(t)}\mathbf{A}_{\mathbf{1}}\mathbf{+ (1 - D(t))}\mathbf{A}_{\mathbf{2}}\mathbf{=}D(t)\begin{bmatrix} \frac{- \left( R_{L1} + R_{on} \right)}{L_{1}} & 0 \\ 0 & 0 \end{bmatrix} + (1 - D(t))\begin{bmatrix} \frac{- \left( R_{L1} + R_{C1} \right)}{L_{1}} & \frac{- 1}{L_{1}} \\ \frac{1}{C_{1}} & 0 \end{bmatrix}$
$\begin{bmatrix} \frac{- R_{L1} - D(t)R_{on} - (1 - D(t))R_{C1}}{L_{1}} & \frac{- (1 - D(t))}{L_{1}} \\ \frac{(1 - D(t))}{C_{1}} & 0 \end{bmatrix}$
$[1L1RC1L1−1L10−1C10]{\mathbf{B = D(t)}\mathbf{B}_{\mathbf{1}}\mathbf{+ (1 - D(t))}\mathbf{B}_{\mathbf{2}}\mathbf{=}D(t)\begin{bmatrix} \frac{1}{L_{1}} & 0 & 0 \\ 0 & \frac{- 1}{C_{1}} & 0 \end{bmatrix} + (1 - D(t))\ \begin{bmatrix} \frac{1}{L_{1}} & \frac{R_{C1}}{L_{1}} & \frac{- 1}{L_{1}} \\ 0 & \frac{- 1}{C_{1}} & 0 \end{bmatrix} }$
$\begin{bmatrix} \frac{1}{L_{1}} & \frac{R_{C1}(1 - D(t))}{L_{1}} & \frac{- (1 - D(t))}{L_{1}} \\ 0 & \frac{- 1}{C_{1}} & 0 \end{bmatrix}$
$C=D(t)C1+(1−D(t))C2=D(t)[01]+(1−D(t))[RC11]{\mathbf{C = D(t)}\mathbf{C}_{\mathbf{1}}\mathbf{+ (1 - D(t))}\mathbf{C}_{\mathbf{2}}\mathbf{=}D(t)\begin{bmatrix} 0 & 1 \end{bmatrix} + (1 - D(t))\begin{bmatrix} R_{C1} & 1 \end{bmatrix} }$
$\left\lbrack (1 - D(t))\begin{matrix} R_{C1} & 1 \end{matrix} \right\rbrack$
$E=D(t)E1+(1−D(t))E2=D(t)[0−RC10]+(1−D(t))[0−RC10]{\mathbf{E = D(t)}\mathbf{E}_{\mathbf{1}}\mathbf{+ (1 - D(t))}\mathbf{E}_{\mathbf{2}}\mathbf{=}D(t)\begin{bmatrix} 0 & - R_{C1} & 0 \end{bmatrix} + (1 - D(t))\begin{bmatrix} 0 & - R_{C1} & 0 \end{bmatrix} }$
$\begin{bmatrix} 0 & - R_{C1} & 0 \end{bmatrix}$