Hi!探索者们😉,欢迎踏入 408 数据结构的奇妙秘境🌿!
我是 ankleless📚,和你并肩的寻宝人~ 这是我的探险手札🗺️,里面记着链表森林的岔路陷阱🕸️、栈与队列城堡的机关密码🔐、二叉树山脉的攀登技巧🚶♀️,还有哈希表迷宫的快捷密道🌀,盼着能帮你避开数据结构的暗礁险滩🌊。
愿我们在算法峡谷🌄各自披荆斩棘,在复杂度峰顶🥇击掌相庆,共观数据流转的星河璀璨🌠!冲呀!🚀
目录
编辑
1. 栈
1.1 基本概念
1.1.1 栈的定义
1.1.2 栈的基本操作
1.2 存储结构
1.2.1 顺序存储
1.顺序栈的实现
2. 顺序栈的基本操作
1.2.2 共享栈
1.2.3 链式存储
2. 队列
2.1 基本概念
2.1.1 队列的定义
2.2.2 队列常见的基本操作
2.2 队列的顺序存储结构
2.2.1 队列的顺序存储
1. 栈
1.1 基本概念
1.1.1 栈的定义
栈(Stack)是只允许在一端进行插入或删除操作的线性表。首先栈是一种线性表,但限定这种线性表只能在某一端进行插入和删除操作。这种逻辑规则类似于手枪子弹的装载和卸下,如下图所示:
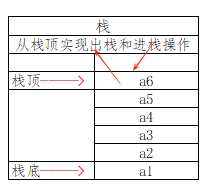
栈顶(Top):线性表允许进行插入和删除的一端(出栈和进栈);
栈底(Bottom):固定的,不允许进行插入和删除的另一端;
空栈:不含任何元素的空表;
进栈(Push):将一个新的元素添加到栈的栈顶的操作,新的元素会成为当前栈中新的栈顶;
出栈(Pop):将栈的栈顶元素从栈中移除,由于栈只能操作栈顶,出栈后,原栈顶的下一个元素称为新的栈顶。
如:
假设某个栈S=(a1, a2, a3, a4, a5, a6)(如上图),那么我们可以知道a1为栈底元素,a6位栈顶元素。栈只能在栈顶进行插入和删除操作,进栈次序依次为a1, a2, a3, a4, a5, a6;而出栈次序为a6, a5, a4, a3, a2, a1。由此可见,栈的操作特性可以明显概括为后进先出(Last In First Out,LIFO)
注:每接触一种新的数据结构,都应从逻辑结构、存储结构和运算三个方面着手(数据结构的三大要素)
1.1.2 栈的基本操作
栈(Stack)后进先出(Last In First Out,LIFO)的特性决定了他是一种受限的访问方式,仅允许在栈顶进行操作,他的基本操作如下:
#define Maxsize 50//定义栈中元素的最大个数typedef int Elemtype;//重定义类型名称struct Sqstack
{Elemtype data[Maxsize];//存放栈中元素,底层是数组int top;//栈顶指针
};typedef struct Sqstack Sqstack;//重定义void InitStack(Sqstack* S);//初始化一个栈,传入指针bool StackEmpty(Sqstack S);//判断一个栈是否为空,若栈S为空则返回true,否则返回falsevoid Push(Sqstack* S, Elemtype x);//压栈,若栈S未满,则将x加入使之成为新栈顶void Pop(Sqstack* S, Elemtype* x);//出栈,若栈S非空,则用x返回栈顶元素void GetTop(Sqstack S, Elemtype* x);//读取栈顶元素,但不出栈,若栈S非空,则用x返回栈顶元素void DestroyStack(Sqstack* S);//销毁栈,并释放栈S占用的存储空间,在C++中"&"表示引用调用注:此处栈的存储结构为顺序存储,底层是数组,由于栈的逻辑结构的限制,我们不能够使用违反其逻辑结构的操作,如修改,头插等(逻辑结构会显著影响数据的运算)
在解答算法题时,若题干未做出限制,则也可以直接使用这些基本的操作函数;
栈的数学性质:当n个不同元素进栈时,出栈元素不同排列的个数为\(C_n = \frac{1}{n+1} \binom{2n}{n}\),即卡特兰数。其中,\(\binom{2n}{n}\) 是组合数,表示从 2n 个元素中选择 n 个的组合数。
1.2 存储结构
栈是一种操作受限的线性表,类似于线性表,他也有对应的两种存储方式
1.2.1 顺序存储
1.顺序栈的实现
采用顺序存储的栈称为顺序栈,它利用一组地址连续的存储单元存放自栈底到栈顶的数据元素,同时附设一个指针(top)指示当前栈顶元素的位置。
栈的顺序存储类型可描述为:
#define Maxsize 50//定义栈中元素的最大个数typedef int Elemtype;//重定义类型名称struct Sqstack
{Elemtype data[Maxsize];//存放栈中元素,底层是数组int top;//栈顶指针
};栈顶指针:S.top,初始时设置S.top = -1;
栈顶元素:S.data[S.top];
进栈操作:栈不满时,栈顶指针先加1,再送值到栈顶;
出栈操作:栈非空时,先取栈顶元素,再将栈顶指针减一;
栈空条件:S.top == -1;
栈满条件:S.top == Maxsize - 1;
栈长:S.top + 1。
另一种常见的方式是:初始设置栈顶指针 S.top = 0;进栈时先将值送到栈顶,栈顶指针再加1;出栈时,栈顶指针先减1;再取栈顶元素;栈空的条件是S.top == 0;栈满条件是 S.top == Maxsize
顺序栈的入栈操作受数组上界的约束,当对栈的最大使用空间估计不足时,有可能会发生栈上溢,此时应及时向用户报告信息,以便及时处理,避免出错。
注:栈和队列的判空、判满条件,会因实际给的条件不同而变化,下面的代码实现是在栈顶指针初始化-1的条件下的相应方法,而其他情况则需要具体情况具体分析。
2. 顺序栈的基本操作
我们采用第一种方式对顺序栈进行基本操作,如下图,当栈空时S.top === -1;当进行压栈和出栈操作时,S.top会指向新的栈顶。

下列是顺序栈上常用的基本操作的实现。
(1)初始化
void InitStack(Sqstack* S)//初始化一个栈,传入指针
{S->top = -1;//此时栈为空表
}(2)判栈空
bool StackEmpty(Sqstack S)//判断一个栈是否为空,若栈S为空则返回true,否则返回false
{if (S.top == -1)return true;elsereturn false;
}(3)压栈
void Push(Sqstack* S, Elemtype x)//压栈,若栈S未满,则将x加入使之成为新栈顶
{if (S->top == Maxsize - 1){printf("栈满,无法压栈\n");return;}S->top++;//先+1S->data[S->top] = x;//后输入return;
}(4)出栈
void Pop(Sqstack* S, Elemtype* x)//出栈,若栈S非空,则用x返回栈顶元素
{if (S->top == -1){printf("栈空,无法出栈\n");return;}*x = S->data[S->top];//先赋值S->top--;//再-1return;}
(5)读栈顶元素
void GetTop(Sqstack S, Elemtype* x)//读取栈顶元素,但不出栈,若栈S非空,则用x返回栈顶元素
{if (S.top == -1){printf("栈空,无栈顶元素\n");return;}*x = S.data[S.top];printf("栈顶元素为%d\n", *x);return;
}仅为读取栈顶元素,并没有出栈操作,因此原栈顶元素依然保留在栈中。
(6)销毁栈
void DestroyStack(Sqstack* S)//销毁栈,并释放栈S占用的存储空间,在C++中"&"表示引用调用
{S->top == -1;printf("栈销毁成功\n");
}注:这里的top指向的是栈顶元素,于是,进栈操作为S->data[++S->top] = x,出栈操作位*x = S->data[S->top--]。若栈顶指针初始化为S.top=0,即top指向栈顶元素的下一个位置,则入栈操作变为S->data[S->top++] = x;出栈操作变为*x = S->data[--S->top]。相应的栈空、栈满条件也会发生变化,需要灵活思考,这一点也可以类比链表中的有无头结点情况
1.2.2 共享栈
利用栈底位置相对不变的特性,可以让两个顺序栈共享一个一维数组空间,将两个栈的栈底分别设置在共享空间的两端,两个栈顶向共享空间的中间延伸。

两个栈的栈顶指针都指向栈顶元素,top0 == - 1时0号栈为空,top1 = Maxsize时,1号栈为空;仅当两个栈顶指针相邻(top1 - top0 == 1)时,判断栈满。当0号栈入栈时 top0先加1再赋值,1号栈入栈时top1先减一再赋值;出栈时则刚好相反。
共享栈是为了更有效地利用存储空间,两个栈的空间相互调节,只有在整个存储空间被占满时才发生上溢。其存储数据的时间复杂度均为O(1) ,所以对存储效率没有什么影响。
1.2.3 链式存储
采用链式存储的栈称为链栈,链栈的优点便是便于多个栈共享存储空间和提高其效率,且不存在栈满上溢的情况。通常采用单链表实现链栈,并规定所有操作都是在单链表的表头(视为栈顶)进行的。此处的举例规定链栈没有头结点,Lhead指向栈顶元素,Lhead称为栈顶指针(不要和单链表的表头指针名称搞混)。
栈的链式存储类型可描述为
struct Linkstack
{Elemtype data;//存储数据struct Linkstack* next;//指针域,指向下一个结点
};采用链式存储,便于结点的插入和删除。链栈的操作和链表类似,入栈和出栈的操作都在链表的表头进行。需要注意的是,对于带头结点和不带头结点的链栈,具体的实现会有不同。
关于链栈的基本操作的实现将在后续的代码中进行介绍。
2. 队列
2.1 基本概念
2.1.1 队列的定义
队列(queue)简称队,也是一种操作受限的线性表,只允许在表的一段进行插入,而在表的另一端进行删除。向队列中插入元素称为入队或进队;删除元素称为出队或离队。这和我们日常生活中的排队是一致的,最早排队的也是最早离队的,其操作的特性是先进先出(First In First Out,FIFO)
队头(Front):允许删除的一端,也称为队首。
队尾(Rear):允许插入的一端。
空队列(Empty):不含任何元素的空表。
2.2.2 队列常见的基本操作
#define Maxsize 50typedef int Elemtype;//顺序存储结构-静态数组
typedef struct
{Elemtype data[Maxsize];//用数组存放队列元素int front, rear;//队首指针和队尾指针,他们具备指针的作用,但不是真正的指针
}SqQueue;typedef SqQueue SQ;bool InitQueue(SQ* Q);//初始化队列,构造一个空队列Qbool QueueEmpty(SQ Q);//判队列空,若队列空返回true,否则返回falsebool EnQueue(SQ* Q,Elemtype x);//入队,若队列Q未满,将x加入,使之称为新的队尾。Elemtype DeQueue(SQ* Q);//出队,若队列Q非空,删除队首元素,用x返回bool GetHead(SQ Q, Elemtype* x);//读队首元素,若队列Q非空,则将队首元素赋值给x
注:栈和队列是操作受限的线性表,因此不是任何对线性表的操作都可以作为栈和队列的操作。比如,不可以随便读取栈或者队列中间的某个数据。
2.2 队列的顺序存储结构
2.2.1 队列的顺序存储
队列的顺序实现是指分配一块连续的存储单元存放队列中的元素,并附设两个指针:队首指针front指向队首元素,队尾指针rear指向队尾元素的下一个位置(不同的版本或作者对front和rear的定义肯不同,这也会导致后续操作的代码设置有所不同,需要根据具体问题具体分析)
队列的顺序存储类型可描述为
#define Maxsize 50typedef int Elemtype;//顺序存储结构-静态数组
typedef struct
{Elemtype data[Maxsize];//用数组存放队列元素int front, rear;//队首指针和队尾指针
}SqQueue;初始时:Q.front = Q.rear = 0;
入队操作:队不满时,先送值到队尾元素,再将队尾指针加一;
出队操作:队不空时,先取队首元素值,再将队首指针加一;
如下图所示,当队列初始化时,有 Q.front = Q.rear = 0成立,此时为空队列;当队列进行出队五次的操作后,有 Q.front = Q.rear成立,此时为空队列,故而Q.front = Q.rear可以作为队列判空的条件。
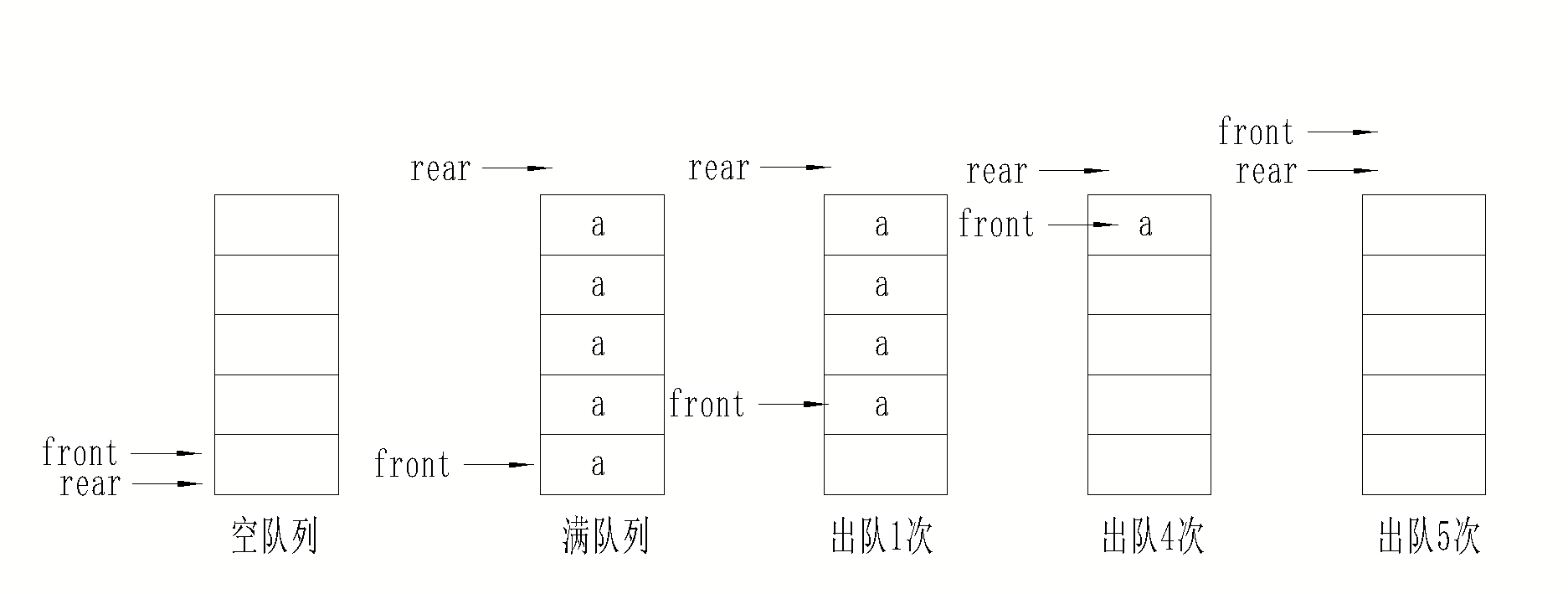
思考一下:能否用Q.rear == Maxsize作为队列满的判断条件呢?
答案显然是不能,当出队4次后,队列中仅有一个元素,但此时仍满足改条件。这时入队出现“上溢出”,但这种溢出并不是真正的溢出,在data数组中依然存在可以存放元素的空位置,所以是一种“假溢出”。
2.2.2 循环队列
针对顺序队列“假溢出”的问题,循环队列可以很好地解决。
循环队列是将顺序队列抽象成一个环状的空间,即把存储队列元素的表从逻辑上视为一个环,称为循环队列。当队首指针Q.front == Maxsize - 1后,再前进一个位置就自动到0,这可以利用除法取模运算(%)来实现。
初始时:Q.front = Q.rear = 0;
队首指针进1:Q.front = (Q.front + 1)%Maxsize;
队尾指针进1:Q.rear= (Q.rear + 1)%Maxsize;
队列长度:(Q.rear + Maxsize - Q.front)%Maxsize;(此式子需要加强理解)
出入队时:指针都按顺时针方向进一,如下图: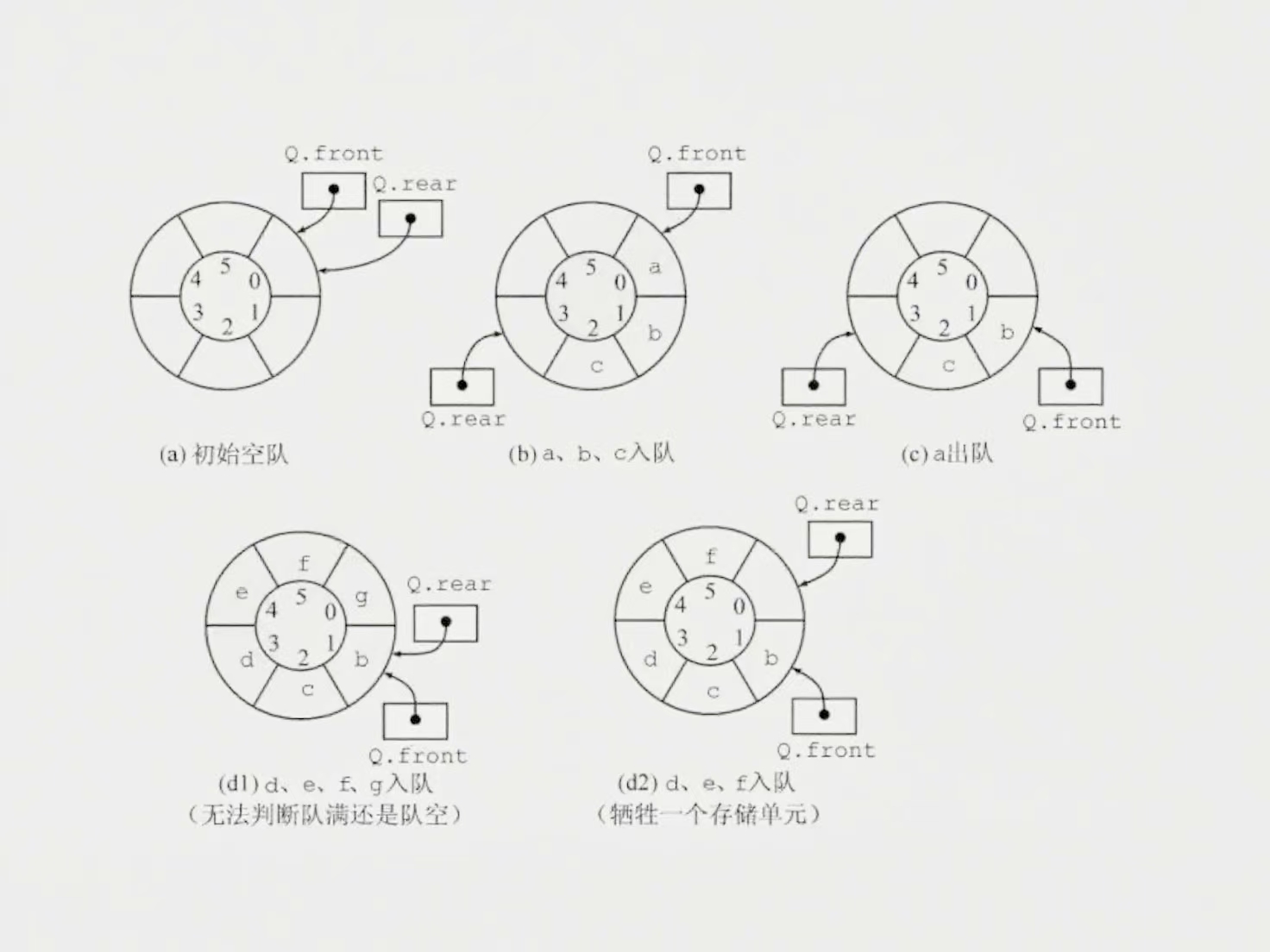
为了区分是队空还是队满的情况,有三种处理方式:
1)牺牲一个单元来区分队满和队空。入队时少用一个队列单元,这是一种较为普遍的做法,约定以“队首指针在队尾指针的下一个位置作为队满的标志”,如上图(d2)所示。
这种情况的判空判满十分重要
队满条件:(Q.rear + 1)%Maxsize == Q.front;
队空条件:Q.front = Q.rear;
队列中元素的个数:(Q.rear + Maxsize - Q.front)%Maxsize。
2)类型中增设size数据成员,表示元素个数。若删除成功,则size减1,若插入成功,则size加1,队空时,Q.size == 0;队满时,Q.size == Maxsize,这两种情况都有Q.front = Q.rear。
3)类型中增设tag数据成员,以区分是队满还是队空。删除成功置tag = 0,若导致Q.front = Q.rear,则队空;插入成功置tag = 1,若导致Q.front = Q.rear,则队满。
2.2.3 循环队列的基本操作
(1)初始化
bool InitQueue(SQ* Q)//初始化队列,构造一个空队列Q
{Q->front = Q->rear = 0;//初始时两个指针重合,且均为0return true;
}(2)判队空
bool QueueEmpty(SQ Q)//判队列空,若队列空返回true,否则返回false
{if (Q.front == Q.rear)return true;elsereturn false;
}(3)入队
bool EnQueue(SQ* Q, Elemtype x)//入队,若队列Q未满,将x加入,使之称为新的队尾。
{if ((Q->rear +1)%Maxsize == Q->front)//栈满,这个是循环队列的判断方式{printf("栈满,无法插入\n");return false;}Q->data[Q->rear] = x;//插入数据Q->rear = (Q->rear + 1) % Maxsize;return true;
}(4)出队
Elemtype DeQueue(SQ* Q)//出队,若队列Q非空,删除队首元素,用x返回
{if (Q->front == Q->rear){printf("栈空,无元素\n");return -1;}Elemtype x = Q->data[Q->front];//先保存返回值Q->front = (Q->front + 1) % Maxsize;//随后队首指针++return x;
}2.3 队列的链式存储结构
2.3.1 队列的链式存储
队列的链式表示称为链式队列,它实际上是一个同时有队首指针和队尾指针的单链表,如下图。队首指针指向队头结点(出队端),队尾指针指向队尾结点(入队端),即单链表的最后一个结点。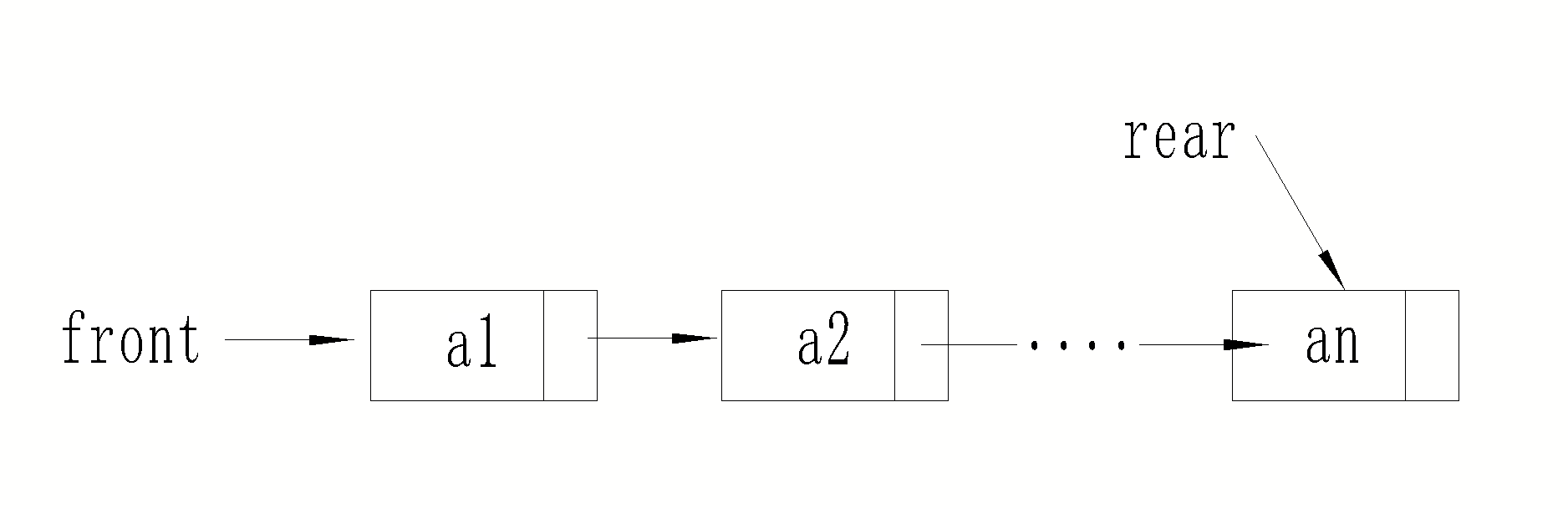
队列的链式存储类型可表述为
typedef struct LinkNode//链式队列结点
{Elemtype data;//用数组存放队列元素struct LinkNode* next;//指向下一个结点
}LinkNode;typedef struct//链式队列
{struct SqQueue* front;//队首指针,出队端struct SqQueue* rear;//队尾指针,入队端
}LinkQueue;不带头结点时,当Q.front == NULL且Q.rear ==NULL时,链式队列为空。
带头结点时,当Q.front == Q.rear且LHead->next ==NULL时,链式队列为空。
入队时,建立一个新结点,将新结点插入到链表的尾部,并让Q.rear指向这个新插入的结点(若原队列为空队,则令Q.front也指向该结点)。出队时,首先判断队是否为空,若不空,则取出队首元素,将其从链表中删除,并让Q.front指向下一个结点(若该结点为最后一个节点,则置Q.front和Q.rear都为NULL)。
不难看出,不带头结点的链式队列在操作上往往比较麻烦,因此通常将链式队列设计成一个带头结点的单链表,这样插入和删除操作就统一了,下图为带头结点的链式队列。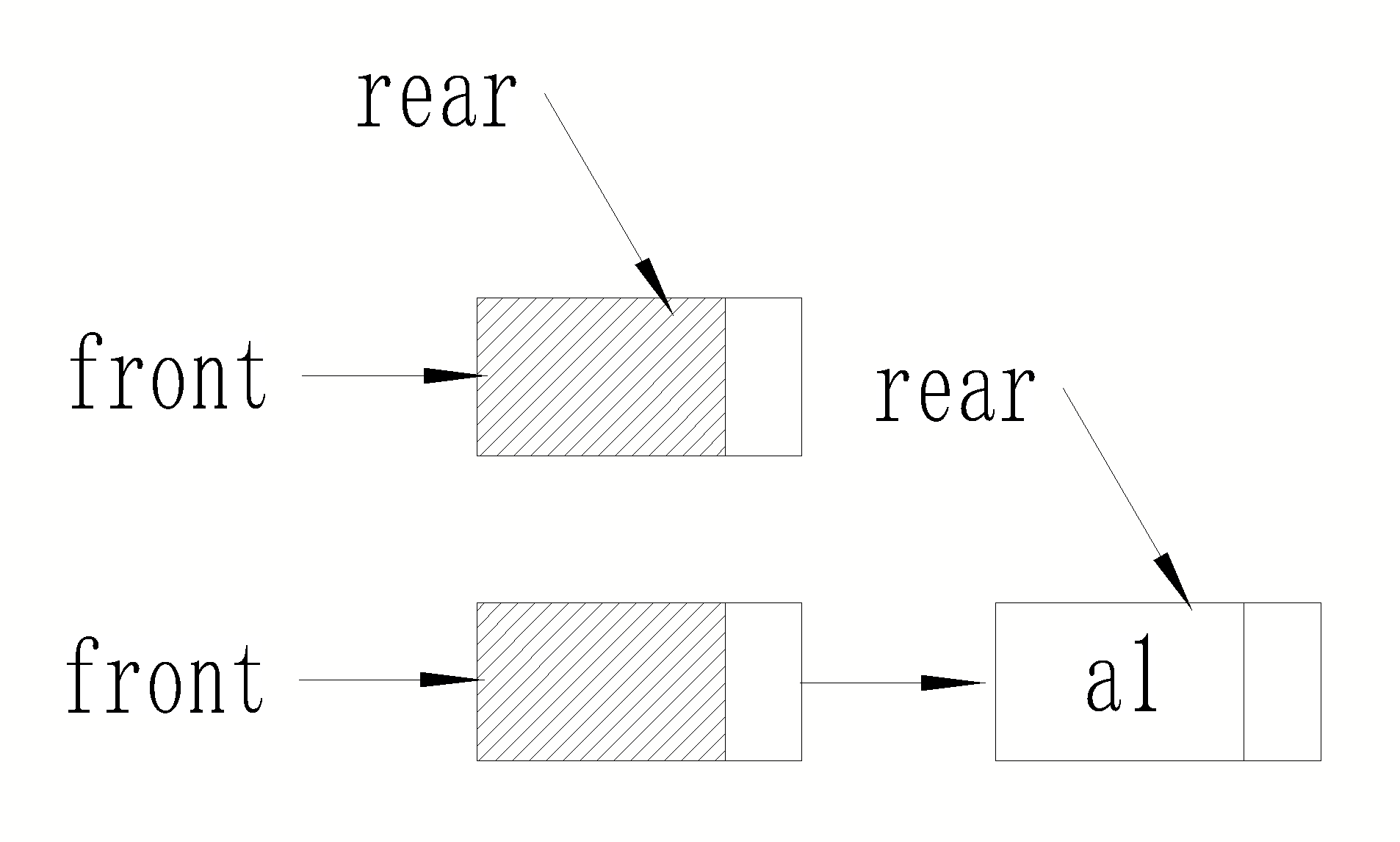
用单链表表示的链式队列特别适合于数据元素变动比较大的情形,而且不存在队列满且产生溢出的问题。另外,假如程序中要使用多个队列,与多个栈的情形一样,最好使用链式队列,这样就不会出现存储分配不合理和“溢出”的问题。
2.3.2 链式队列的基本操作
(1)初始化
bool InitQueue(LinkQueue* Q)//初始化带头结点的链式队列
{Q->front = Q->rear = (LinkNode*)malloc(sizeof(LinkNode));if (Q->front == NULL){perror("malloc\n");return false;}Q->front->next = NULL;return true;
}(2)判队空
bool QueueEmpty(LinkQueue* Q)//判队列空,若队列空返回true,否则返回false
{if (Q->front == Q->rear)//判空条件return true;elsereturn false;
}
(3)入队
ool EnQueue(LinkQueue* Q, Elemtype x)//入队,若队列Q未满,将x加入,使之称为新的队尾。
{//没有溢出风险LinkNode* q = (LinkNode*)malloc(sizeof(LinkNode));//创建存储数据的结点if (q == NULL){perror("malloc\n");return false;}q->data = x;//载入数据q->next = NULL;Q->rear->next = q;Q->rear = q;//修改队尾指针return true;}(4)出队
bool DeQueue(LinkQueue* Q, Elemtype* x)//出队,若队列Q非空,删除队首元素,用x返回
{if (Q->front == Q->rear){printf("栈空\n");return false;}LinkNode* q = Q->front->next;//储存要出队的结点地址*x = q->data;//x返回值Q->front->next = q->next;if (Q->rear = q)Q->rear = Q->front;//如果只有一个结点,删除后变空free(q);q = NULL;return true;
}

 等实战代码,免费股票数据接口大全)



 -- MQTT篇)
”)




)







