题目一：剪花布条

题目链接：剪花布条

【题目描述】

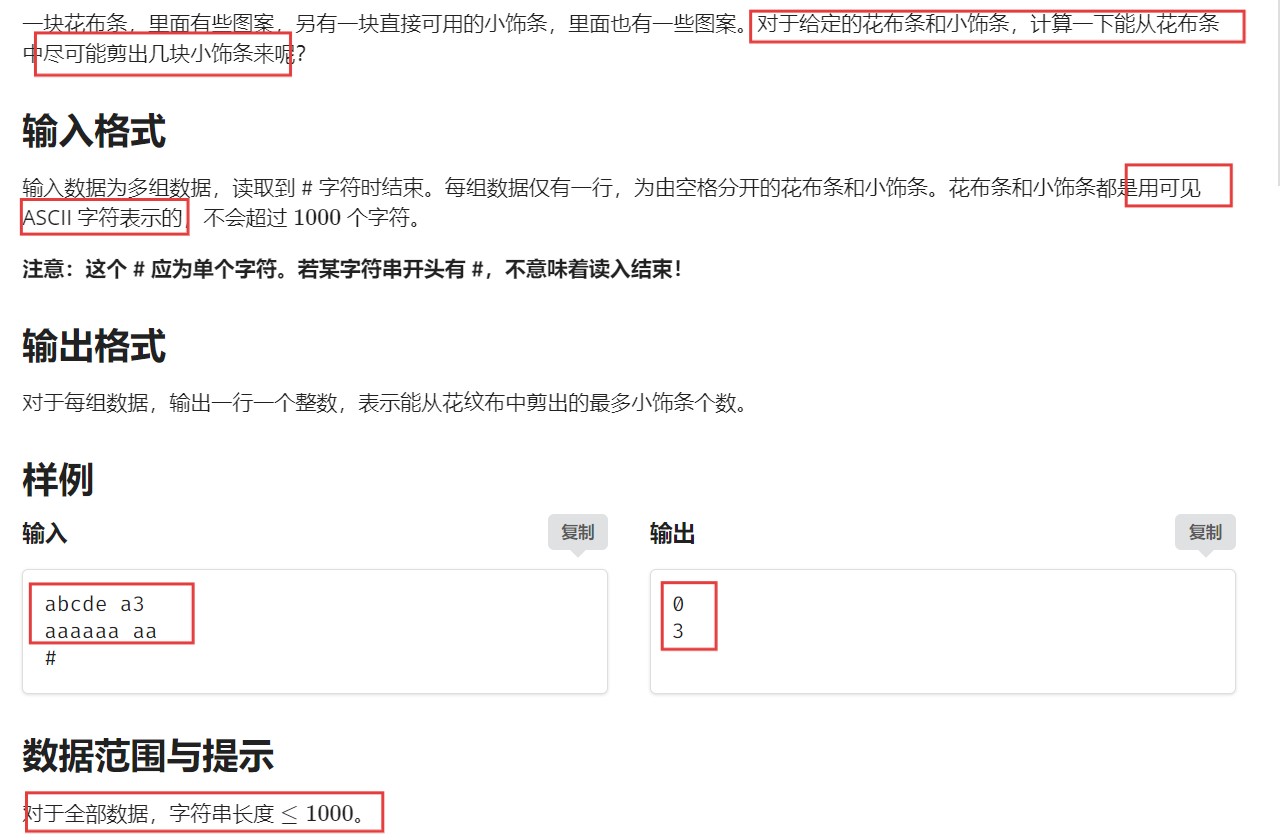
【算法原理】

这道题一眼就可以看出是字符串匹配的问题，暴力解法当然是拿着模式串去主串的每一个位置依次进行匹配，时间复杂度较高，但是这道题目数据范围比较小，应该也是可以通过~~

这种字符串匹配的问题，我们可以尝试使用 KMP 算法进行解决。

但不同于 KMP 算法模板题的是，这道题目找到所有匹配的位置之后，还要从左到右进行判断筛选，不能重叠。这个只需要额外判断匹配位置之间的距离是否大于模式串的长度就可以了。

注意：可见的 ASCII 字符是包括 ‘#’ 的，因此我们用 ‘ ’（空格）来链接模式串和主串。

【代码实现】

#include <iostream>using namespace std;const int N = 2010; // 注意要开成两倍 string s, t;
int n, m;
int pi[N];int main()
{while(cin >> s >> t){int ret = 0; n = s.size(); m = t.size();s = ' ' + t + ' ' + s;for(int i = 2; i <= m + n + 1; i++){int j = pi[i - 1];while(j && s[i] != s[j + 1]) j = pi[j];if(s[i] == s[j + 1]) j++;pi[i] = j;}for(int i = m + 1; i <= m + n + 1; i++){if(pi[i] == m){ret++;i += m - 1; // 出去以后还会 ++ 一次 // 防重叠 }}cout << ret << endl;}return 0;
}

题目二：Seek the Name

题目链接：Seek the Name

【题目描述】

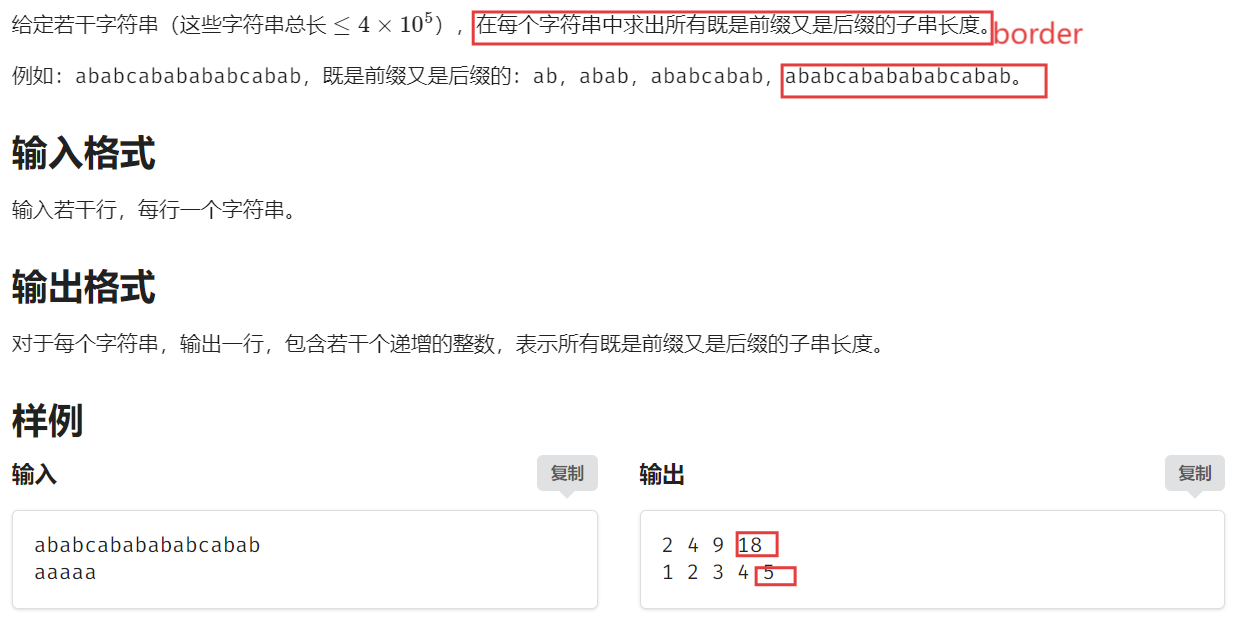
【算法原理】

前缀函数的小用途~~

border 的 border 还是 border

题目要求求出字符串所有 border 的长度，我们可以先求出最长的 border 的长度，再依次去找短的 border。这道题目就是一个简单的求前缀函数的问题~~

用数组存储所有 border 的长度，最后再逆序输出。（有一种数组模拟栈的感觉）

最后不要忘记输出整个字符串的长度~~，求 border 不会考虑，但是本题是要考虑的。

【代码实现】

#include <iostream>using namespace std;const int N = 4e5 + 10;string s;
int n, pi[N];
int ret[N], top;int main()
{while(cin >> s){top = 0;n = s.size();s = ' ' + s;for(int i = 2; i <= n; i++){int j = pi[i - 1];while(j && s[i] != s[j + 1]) j = pi[j];if(s[i] == s[j + 1]) j++;pi[i] = j;}for(int i = pi[n]; i; i = pi[i]) ret[++top] = i;for(int i = top; i >= 1; i--) cout << ret[i] << " ";cout << n << endl;}return 0;
}

题目三：ABB

题目链接 ABB

【题目描述】

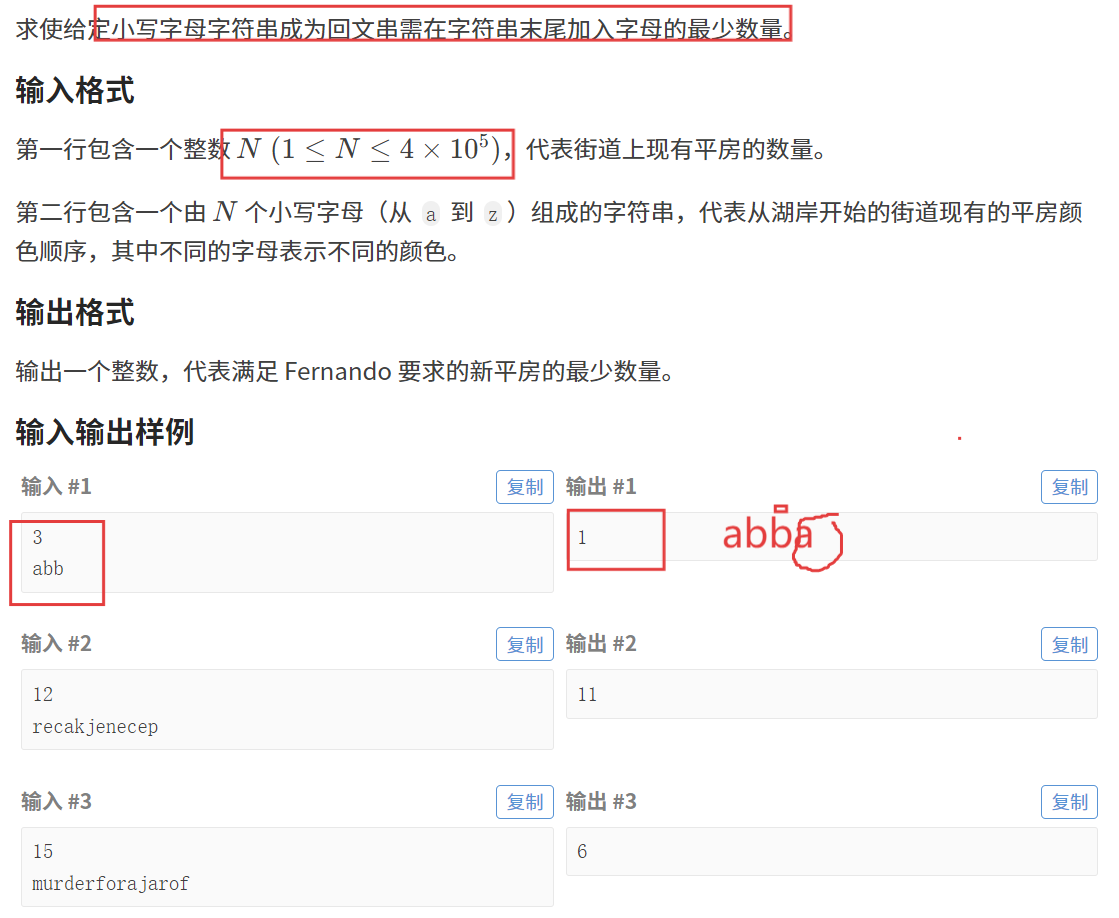
【算法原理】

对于回文串相关的问题，可以使用 malache 算法来解决，但是我们这个专题是 KMP，因此我们尝试使用 KMP 算法来解决这个问题。

题目转化：这道题实质上是求给定字符串的最长回文后缀的长度 len，n - len 就是最终结果。

因为题目要求你只能从字符串的末端去补充字符，所以回文后缀的长度越长，你要补充的字符数量就越少。

所以我们只需要解决求出一个字符串的最长回文后缀的长度就可以了~~

如何解决这个问题呢？？？

我们发现：如果将回文串逆序，应该和原始的字符串相同。因此，我们可以将字符串逆序之后拼接到原始字符串的前面，在中间加一个 ‘#’ 连接。

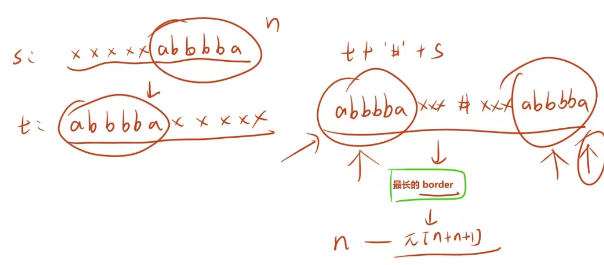
接下来，我们只需要求出新字符串最长的 border 长度 pi，再用 n - pi 就解决了。

【代码实现】

#include <iostream>
#include <algorithm>using namespace std;const int N = 8e5 + 10; // 开两倍 string s, t;
int n;
int pi[N];int main()
{cin >> n >> s;t = s;reverse(t.begin(), t.end());s = ' ' + t + '#' + s;for(int i = 2; i <= n + n + 1; i++){int j = pi[i - 1];while(j && s[i] != s[j + 1]) j = pi[j];if(s[i] == s[j + 1]) j++;pi[i] = j;}cout << n - pi[n + n + 1] << endl;return 0;
}

题目四：Censoring S

题目链接：Censoring S

【题目描述】

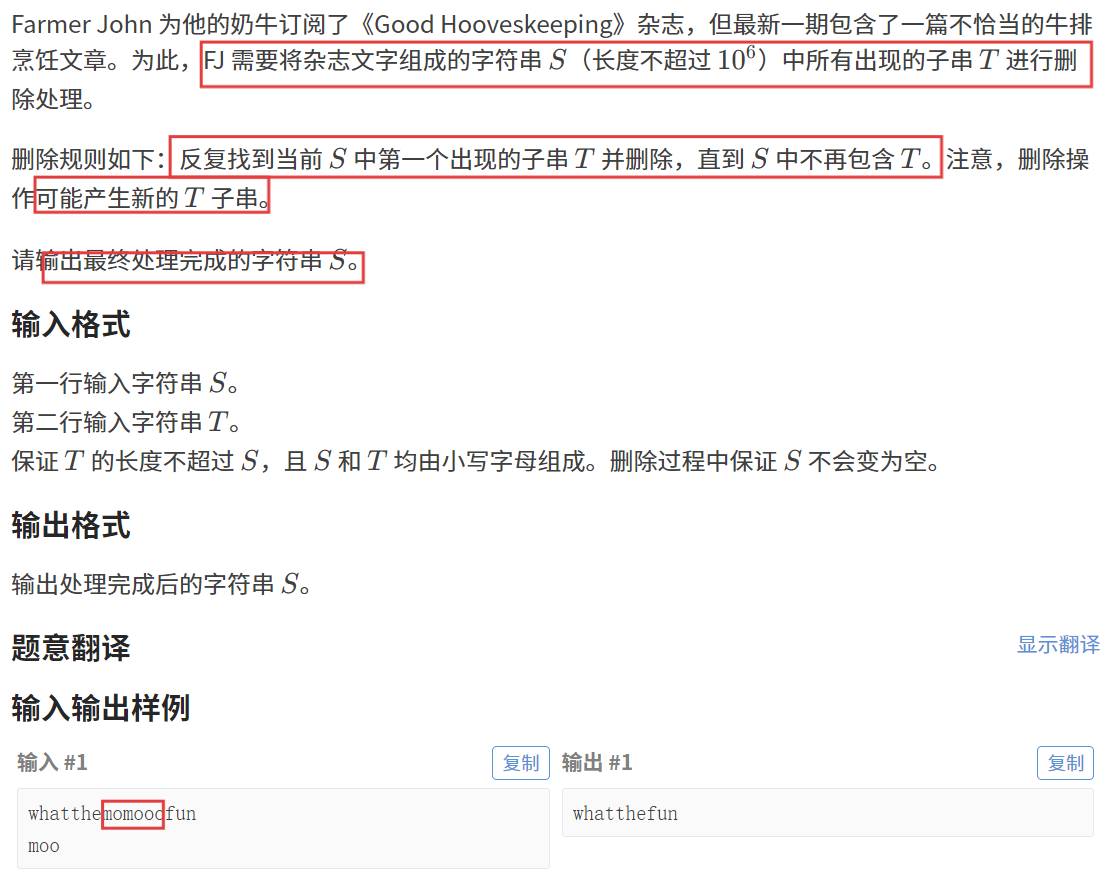
【算法原理】

KMP 算法 + 栈（存下标）

对于这种类似”消消乐“的玩法，我们很容易想到 “栈” 这样的一个数据结构。

对于之前求前缀函数的模板，我们优先考虑使用【1，i - 1】的 border 来更新【1，i】的 border

但是这道题目涉及消除的操作，因此我们不能使用【1，i - 1】的 border 来更新【1，i】的 border（有可能前面的字符都消没了）

而是使用栈顶下标的元素来更新【1，i】的 border。

【代码实现】

#include <iostream>using namespace std;const int N = 2e6 + 10;string s, t;
int n, m, pi[N];
int st[N], top; // 用数组模拟栈 int main()
{cin >> s >> t;n = s.size(), m = t.size();s = ' ' + t + ' ' + s;// pi[1] = 0;st[++top] = 1;for(int i = 2; i <= n + m + 1; i++){int j = pi[st[top]];while(j && s[i] != s[j + 1]) j = pi[j];if(s[i] == s[j + 1]) j++;pi[i] = j;st[++top] = i;if(j == m){for(int k = 0; k < m; k++) top--;}}for(int i = m + 2; i <= top; i++) cout << s[st[i]];return 0;
}

好的，今天的分享到这里就结束了，谢谢大家！！！