本文参考文章0.0 目录-深度学习第一课《神经网络与深度学习》-Stanford吴恩达教授-CSDN博客

1.调试处理

神经网络的改变会涉及到许多不同的超参数设置，现在，对于超参数而言，如何找到一套比较好的设定？

训练深度最难的事之一是你要处理的参数数量，从学习率 $\alpha$ 到动量梯度下降的参数 $\beta$ ，也许还有层数，隐藏单元数量，学习率衰减等

吴恩达教授认为，学习速率是需要调试的最重要的超参数。

现在，如果你尝试调整一些超参数，该如何选择调试值呢？在早一代的机器学习算法中，如果你有两个超参数，这里我会称之为超参1，超参2，常见的做法是在网格中取样点，像这样，然后系统的研究这些数值。这里我放置的是5×5的网格，实践证明，网格可以是5×5，也可多可少，但对于这个例子，你可以尝试这所有的25个点，然后选择哪个参数效果最好。当参数的数量相对较少时，这个方法很实用。

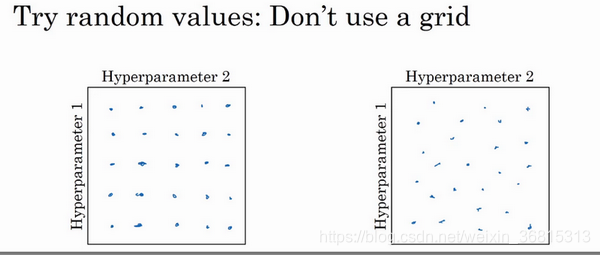
在深度学习领域，推荐你采用下面的做法，随机选择点，所以你可以选择同等数量的点，这里就设为25个点，接着，用这些随机取的点试验超参数的效果。之所以这么做是因为，对于你要解决的问题而言，你很难提前知道哪个超参数最重要，正如你之前看到的，一些超参数的确要比其它的更重要。

实践中，你搜索的超参数可能不止两个。假如，你有三个超参数，这时你搜索的不是一个方格，而是一个立方体，超参数3代表第三维，接着，在三维立方体中取值，你会试验大量的更多的值，三个超参数中每个都是。

实践中，你搜索的可能不止三个超参数有时很难预知，哪个是最重要的超参数，对于你的具体应用而言，随机取值而不是网格取值表明，你探究了更多重要超参数的潜在值，无论结果是什么。

当你给超参数取值时，另一个惯例是采用由粗糙到精细的策略

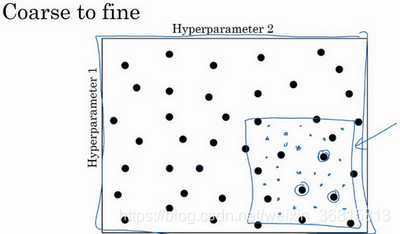
在整个的方格中进行粗略搜索后，你会知道接下来应该聚焦到更小的方格中。在更小的方格中，你可以更密集得取点。所以这种从粗到细的搜索也经常使用。

通过试验超参数的不同取值，你可以选择对训练集目标而言的最优值，或对于开发集而言的最优值，或在超参搜索过程中你最想优化的东西。

2.为超参数选择合适的范围

随机取值并不是在有效范围内的随机均匀取值，而是选择合适的标尺，用于探究这些超参数，这很重要

在隐藏单元数量和神经网络层数等超参数上随机均匀取值是可以的

但是在学习率等超参数上，举个例子，假设你怀疑其值最小是0.0001或最大是1。如果你画一条从0.0001到1的数轴，沿其随机均匀取值，那90%的数值将会落在0.1到1之间，结果就是，在0.1到1之间，应用了90%的资源，而在0.0001到0.1之间，只有10%的搜索资源，这看上去不太对。反而，用对数标尺搜索超参数的方式会更合理，因此这里不使用线性轴，分别依次取0.0001，0.001，0.01，0.1，1，在对数轴上均匀随机取点，这样，在0.0001到0.001之间，就会有更多的搜索资源可用，还有在0.001到0.01之间等等。这里用到的是在对数坐标下取值，取最小值的对数就得到 a 的值，取最大值的对数就得到 b 值，所以现在你在对数轴上的 $10^{a}$ 到 $10^{b}$ ，在a和b间随意均匀的选取r值，将超参数设置为 $10^{r}$

另一个棘手的例子是给 $\beta$ 取值，用于计算指数的加权平均值。假设你认为 $\beta$ 是0.9到0.999之间的某个值，也许这就是你想搜索的范围。记住这一点，当计算指数的加权平均值时，取0.9就像在10个值中计算平均值，有点类似于计算10天的温度平均值，而取0.999就是在1000个值中取平均。

这里探究的是1- $\beta$ = $10^{r}$ 的取值，从0.1到0.001，在a和b间随意均匀的选取r值

总之就是选择合适的标尺（因为有些超参数的微小改变都会对算法产生巨大影响）

3.超参数训练实战：Pandas vs Cavaiar

上面已经讲了关于如何搜索最有超参数的内容，现在我们要谈论如何组织超参数搜索过程

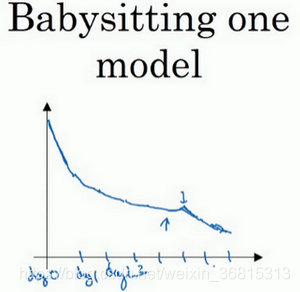
一种是你照看一个模型，通常是有庞大的数据组，但没有许多计算资源或足够的CPU和GPU的前提下，基本而言，你只可以一次负担起试验一个模型或一小批模型，在这种情况下，即使当它在试验时，你也可以逐渐改良。

教授把左边的方法称为熊猫方式。当熊猫有了孩子，他们的孩子非常少，一次通常只有一个，然后他们花费很多精力抚养熊猫宝宝以确保其能成活

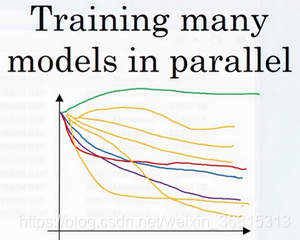
另一种方法则是同时试验多种模型，你设置了一些超参数，尽管让它自己运行，或者是一天甚至多天，然后你会获得像这样的学习曲线，这可以是损失函数J或实验误差或损失或数据误差的损失，但都是你曲线轨迹的度量

对比而言，右边的方式更像鱼类的行为，教授称之为鱼子酱方式。在交配季节，有些鱼类会产下一亿颗卵，但鱼类繁殖的方式是，它们会产生很多卵，但不对其中任何一个多加照料，只是希望其中一个，或其中一群，能够表现出色

4.归一化网络的激活函数

Batch归一化会使你的参数搜索问题变得很容易，使神经网络对超参数的选择更加稳定，超参数的范围会更加庞大，工作效果也很好，也会是你的训练更加容易，甚至是深层网络。

在logisitic回归中，归一化输入特征可以加快学习过程，在更深的模型中，之前已经学习了如何归一化x1,x2,x3，现在来看每层的激活值a，是否也能归一化？实际上归一化的不是a而是z

这里介绍批量归一化（Batch Normalization, BN）

在训练过程中对每一层的输入进行归一化，通常作用于全连接层或卷积层后、激活函数前。公式如下：

$\mu_B = \frac{1}{m}\sum_{i=1}^{m}x_i$

$\sigma_B^2 = \frac{1}{m}\sum_{i=1}^{m}(x_i - \mu_B)^2$

$\hat{x}_i = \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}$

其中 $m$ 为批次大小， $\epsilon$ 为小常数防止除零。最终输出为尺度缩放和偏移的结果：
$y_i = \gamma \hat{x}_i + \beta$ ，这里的 $\gamma ,\beta$ 是你模型的学习参数，所以我们使用梯度下降或一些其它类似梯度下降的算法，正如更新神经网络权重一样可以更新 $\gamma ,\beta$

# 批量归一化
bn = torch.nn.BatchNorm2d(num_features=64)  # 用于卷积层
output = bn(input_tensor)

Batch归一化的作用是它适用的归一化过程，不只是输入层，甚至同样适用于神经网络中的深度隐藏层。你应用Batch归一化了一些隐藏单元值中的平均值和方差，不过训练输入和这些隐藏单元值的一个区别是，你也许不想隐藏单元值必须是平均值0和方差1。

5.将Batch拟合进神经网络

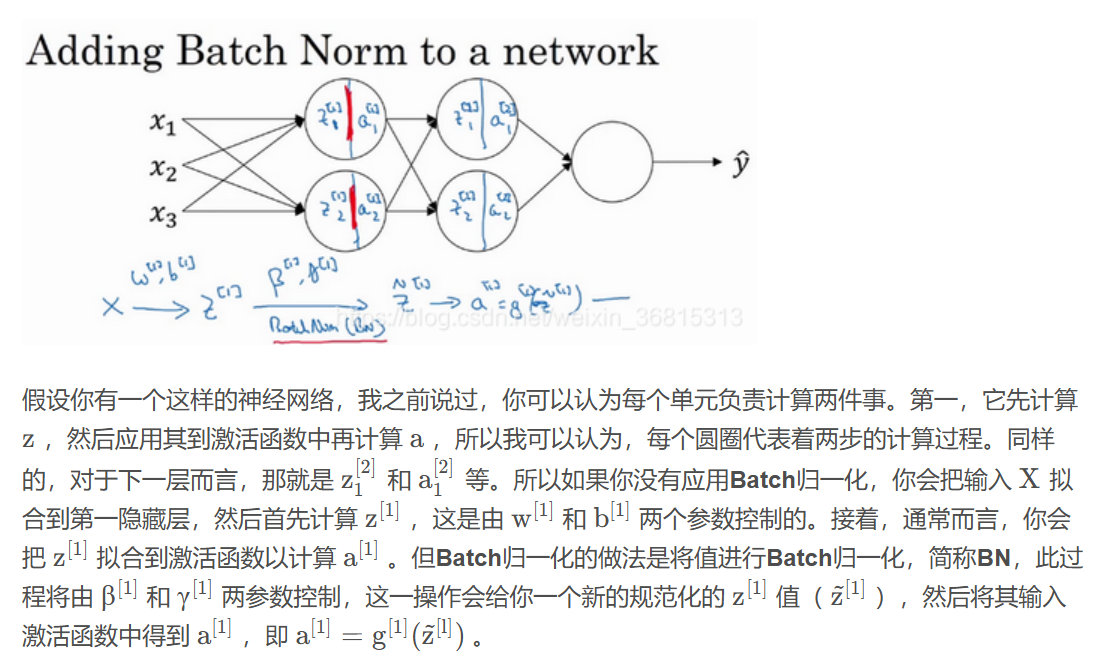
注意：由于要先求均值再减去均值，根据公式加上的任何常数都将会被均值减去所抵消，所以b可以直接消除

from torch.utils.data import DataLoader, TensorDataset# 假设 X 和 y 是输入数据和标签
dataset = TensorDataset(X, y)
batch_size = 32
dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=True)for batch_X, batch_y in dataloader:# 将 batch_X 和 batch_y 输入模型outputs = model(batch_X)loss = criterion(outputs, batch_y)loss.backward()optimizer.step()

6.BatchNorm为什么会起作用

BatchNorm（批归一化）通过标准化每一层的输入分布（均值为0，方差为1），减少内部协变量偏移（Internal Covariate Shift）。这种偏移是指神经网络中前一层的参数更新导致后一层输入分布的变化，从而加剧训练的不稳定性。BatchNorm 通过对每一层的输入进行归一化，使得网络各层的输入分布相对稳定，从而加速训练并提高模型性能。

BatchNorm 通过减少梯度对参数尺度的依赖，使得网络可以使用更高的学习率。传统深度网络中，梯度更新可能导致参数分布剧烈变化，需要谨慎选择学习率。而 BatchNorm 的标准化操作使得梯度更加稳定，允许更大的学习率，从而加快收敛速度。

深度神经网络中，梯度可能在反向传播过程中逐渐消失或爆炸。BatchNorm 通过强制每一层的输入分布保持稳定，使得激活函数的输入值更可能落在梯度较大的区域（如 Sigmoid 函数的线性区间），从而缓解梯度消失或爆炸的问题。

BatchNorm 在训练时对每个批次的均值和方差进行估计，并引入随机噪声（因为批次是随机采样的）。这种噪声类似于 Dropout 的效果，能够轻微地正则化模型，减少过拟合。但需注意，BatchNorm 的主要作用不是正则化，其效果远不如专门的正则化技术（如 Dropout）。

7.测试时的BatchNorm

Batch归一化将你的数据以mini-batch的形式逐一处理，但在测试时，你可能需要对每个样本逐一处理

在mini-batch的基础上，计算一定数量的样本得出每层的 $\mu$ 和 $\sigma ^{2}$

在训练时， $\mu$ 和 $\sigma ^{2}$ 是在整个mini-batch上计算出来的包含了像是64或28或其它一定数量的样本，但在测试时，你可能需要逐一处理样本，方法是根据你的训练集估算 $\mu$ 和 $\sigma ^{2}$ ，估算的方式有很多种，理论上你可以在最终的网络中运行整个训练集来得到 $\mu$ 和 $\sigma ^{2}$ ，但在实际操作中，我们通常运用指数加权平均来追踪在训练过程中你看到的 $\mu$ 和 $\sigma ^{2}$ 的值。还可以用指数加权平均，有时也叫做流动平均来粗略估算 $\mu$ 和 $\sigma ^{2}$ ，然后在测试中使用 $\mu$ 和 $\sigma ^{2}$ 的值来进行你所需要的隐藏单元 z 值的调整。在实践中，不管你用什么方式估算 $\mu$ 和 $\sigma ^{2}$ ，这套过程都是比较稳健的，因此不太会担心你具体的操作方式，而且如果你使用的是某种深度学习框架，通常会有默认的估算 $\mu$ 和 $\sigma ^{2}$ 的方式，应该一样会起到比较好的效果。但在实践中，任何合理的估算你的隐藏单元 z 值的均值和方差的方式，在测试中应该都会有效。

8.Softmax回归

Softmax回归（也称为多项逻辑回归）是逻辑回归的扩展，用于多分类问题（之前的01属于二分类）。它将输入特征通过线性变换映射到多个类别，并通过Softmax函数将输出转化为概率分布。适用于类别互斥且数量大于2的场景。

原理

线性变换部分对每个类别 $k$ 计算得分： $z_k = \mathbf{w}_k^T \mathbf{x} + b_k$

通过Softmax函数将得分转换为概率： $P(y=k|\mathbf{x}) = \frac{e^{z_k}}{\sum_{j=1}^K e^{z_j}}$

其中 $K$ 为类别总数， $\mathbf{w}_k$ 和 $b_k$ 是第 $k$ 个类别的权重和偏置。

损失函数（交叉熵损失）

$J(\mathbf{W}) = -\frac{1}{N} \sum_{i=1}^N \sum_{k=1}^K y_k^{(i)} \log P(y^{(i)}=k|\mathbf{x}^{(i)})$

$y_k^{(i)}$ 是样本 $i$ 的真实类别$k$的指示函数（one-hot编码）， $N$ 为样本数量。

参数优化

通常采用梯度下降法更新参数。权重梯度为： $\frac{\partial J}{\partial \mathbf{w}k} = \frac{1}{N} \sum{i=1}^N \left[ P(y^{(i)}=k|\mathbf{x}^{(i)}) - y_k^{(i)} \right] \mathbf{x}^{(i)}$

偏置项梯度类似： $\frac{\partial J}{\partial b_k} = \frac{1}{N} \sum_{i=1}^N \left[ P(y^{(i)}=k|\mathbf{x}^{(i)}) - y_k^{(i)} \right]$

import numpy as npdef softmax(z):exp_z = np.exp(z - np.max(z, axis=1, keepdims=True))return exp_z / np.sum(exp_z, axis=1, keepdims=True)def cross_entropy_loss(y_true, y_pred):m = y_true.shape[0]return -np.sum(y_true * np.log(y_pred + 1e-15)) / mclass SoftmaxRegression:def __init__(self, learning_rate=0.01, epochs=1000):self.lr = learning_rateself.epochs = epochsdef fit(self, X, y):n_samples, n_features = X.shapen_classes = y.shape[1]self.W = np.zeros((n_features, n_classes))self.b = np.zeros(n_classes)for _ in range(self.epochs):z = np.dot(X, self.W) + self.by_pred = softmax(z)dw = np.dot(X.T, (y_pred - y)) / n_samplesdb = np.mean(y_pred - y, axis=0)self.W -= self.lr * dwself.b -= self.lr * dbdef predict(self, X):z = np.dot(X, self.W) + self.breturn np.argmax(softmax(z), axis=1)

9.训练一个Softmax分类器

Softmax分类器是一种多类分类模型，常用于神经网络输出层。它将输入特征通过线性变换后，应用Softmax函数将得分转换为概率分布，从而预测样本属于各个类别的概率。

数据准备

收集并预处理数据，确保数据格式一致。将数据集分为训练集、验证集和测试集。对特征进行标准化或归一化处理，以加速模型收敛。

import numpy as np
from sklearn.preprocessing import StandardScaler# 假设X是特征矩阵，y是标签向量
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

模型定义

定义Softmax分类器的参数，包括权重矩阵W和偏置向量b。权重矩阵的维度为（特征数 × 类别数），偏置向量的维度为（类别数 × 1）。

n_features = X_train.shape[1]
n_classes = len(np.unique(y_train))# 初始化参数
W = np.random.randn(n_features, n_classes) * 0.01
b = np.zeros((1, n_classes))

前向传播

计算线性得分并通过Softmax函数转换为概率分布。Softmax函数的公式为：

$[ P(y=j|x) = \frac{e^{z_j}}{\sum_{k=1}^{K} e^{z_k}} ]$

其中(z = xW + b)。

def softmax(z):exp_z = np.exp(z - np.max(z, axis=1, keepdims=True))return exp_z / np.sum(exp_z, axis=1, keepdims=True)# 前向传播
def forward(X, W, b):z = np.dot(X, W) + breturn softmax(z)

损失函数

使用交叉熵损失函数（Cross-Entropy Loss）衡量预测概率与真实标签的差异：

$[ L = -\frac{1}{N} \sum_{i=1}^{N} \sum_{j=1}^{K} y_{ij} \log(p_{ij}) ]$

其中 $(y_{ij})$ 是真实标签的独热编码， $(p_{ij})$ 是预测概率。

def cross_entropy_loss(y_true, y_pred):m = y_true.shape[0]log_likelihood = -np.log(y_pred[range(m), y_true])return np.sum(log_likelihood) / m

反向传播和参数更新这里就不介绍了，感兴趣可以自行搜索

训练过程

迭代训练模型，直到损失收敛或达到最大迭代次数。

n_epochs = 1000for epoch in range(n_epochs):# 前向传播y_pred = forward(X_train, W, b)# 计算损失loss = cross_entropy_loss(y_train, y_pred)# 反向传播dW, db = backward(X_train, y_train, y_pred)# 参数更新W, b = update_params(W, b, dW, db, learning_rate)if epoch % 100 == 0:print(f"Epoch {epoch}, Loss: {loss}")

10.深度学习框架

选择框架的标准：

一个重要的标准就是便于编程，这既包括神经网络的开发和迭代，还包括为产品进行配置，为了成千上百万，甚至上亿用户的实际使用，取决于你想要做什么。

第二个重要的标准是运行速度，特别是训练大数据集时，一些框架能让你更高效地运行和训练神经网络。

还有一个标准人们不常提到，但我觉得很重要，那就是这个框架是否真的开放，要是一个框架真的开放，它不仅需要开源，而且需要良好的管理。不幸的是，在软件行业中，一些公司有开源软件的历史，但是公司保持着对软件的全权控制，当几年时间过去，人们开始使用他们的软件时，一些公司开始逐渐关闭曾经开放的资源，或将功能转移到他们专营的云服务中。因此我会注意的一件事就是你能否相信这个框架能长时间保持开源，而不是在一家公司的控制之下，它未来有可能出于某种原因选择停止开源，即便现在这个软件是以开源的形式发布的。但至少在短期内，取决于你对语言的偏好，看你更喜欢Python，Java还是**C++**或者其它什么，也取决于你在开发的应用，是计算机视觉，还是自然语言处理或者线上广告，等等，我认为这里的多个框架都是很好的选择。