推销洛谷博客：https://www.luogu.com.cn/article/znmr9iu9

Link：Luogu - P3907

这里默认题目中指的环都是“简单环”（即没有“环套环”的情况）。

众所周知，树是图的一种特殊情况，且一定无环。如果我们想要得到一个有环的复杂图，有一种办法是考虑先建一棵树，然后不断加入非树边。

那本题如果要“找环”，我们不妨把这个过程反过来。先对于原图中每个连通块都求一棵生成树，因为任意一个简单环都可以又一条非树边和树上的一段路径组成，考虑枚举非树边并判断即可。

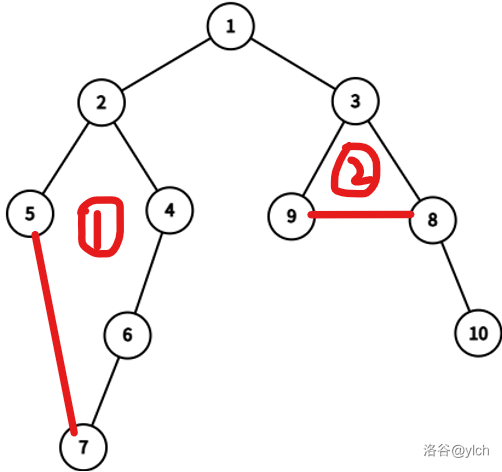
例如上图，环①可以由树上路径 $5-2-4-6-7$ 和非树边 $5-7$ 组成；环②可以由树上路径 $8-3-9$ 和非树边 $8-9$ 组成。

由于异或满足交换律，可以用树上前缀和 + LCA 快速取得某条树上路径的权值异或和。时间复杂度 $O(n\log n)$。

但其实还可以再优化，设 $s_i$ 表示从根结点到 $i$ 的前缀和，在求 $u-v$ 路径的加法权值和时公式是 $s_u+s_v-2\cdot s_{\text{lca(u,v)}}$。但因为异或满足 $x\oplus x=0$，所以在 $s_u\oplus s_v$ 时 $1-\text{lca}(u,v)$ 路径上的异或和就会被自动抵消掉！这样我们就无需求 LCA 了。时间复杂度可以做到 $O(n+m)$。

在求生成树时只要拿一个 $vis$ 数组标记即可，注意特判自环的情况。

#include <bits/stdc++.h>
using namespace std;
const int maxn = 55;vector<array<int, 2>> G[maxn];   // 邻接表：邻接节点，边权
int s[maxn], p[maxn];            // 到根节点的异或和、记录属于的连通块
bool vis[maxn];                  // 标记数组
set<array<int, 2>> treeE;        // 存储树边的有序对
int now;                         // 连通块计数器void dfs(int u, int fa){ // 求生成树+前缀异或和vis[u] = true;p[u] = now;for(auto [v, w] : G[u]){if(v == fa) continue;if(!vis[v]){treeE.insert({min(u, v), max(u, v)}); // 加入生成树中，存储时注意大小关系s[v] = s[u] ^ w;dfs(v, u);}}
}bool solve(){ // 在判断时采取的标准是：如果环不为0一定不行，直接返回；否则虽然当前行但不一定全部都行，继续检查int n, m;cin >> n >> m;// 初始化memset(vis, 0, sizeof(vis));memset(s, 0, sizeof(s));memset(p, 0, sizeof(p));treeE.clear();for(auto &u : G) u.clear();now = 0;vector<tuple<int, int, int>> E; // 存储所有原始边for(int i = 1; i <= m; i ++){int u, v, w; cin >> u >> v >> w;G[u].push_back({v, w}); G[v].push_back({u, w});E.emplace_back(u, v, w);}// 生成树+前缀异或和for(int u = 1; u <= n; u ++){if(!vis[u]){now ++; dfs(u, -1);}}// 检查所有非树边+统计答案for(auto [u, v, w] : E){if(u == v){ // 自环if(w != 0) return false;continue;}if(p[u] != p[v]) continue; // 不同连通块之间无需检查array<int, 2> e = {min(u, v), max(u, v)};if(!treeE.count(e)){ // 检查非树边if((s[u] ^ s[v]) != w) return false;}}return true;
}int main(){cin.tie(nullptr) -> ios::sync_with_stdio(false);int T; cin >> T;while(T --) cout << (solve()? "Yes" : "No") << "\n";return 0;
}

再给一份暴力找环就 AC 的代码：

int vis[55];
vector<array<int, 2>> G[55];bool dfs(int u, int val, int s){ // 当前遍历到u，异或值为val，起点为s时，判定是否正确for(auto [v, w] : G[u]){if(v == s && (val ^ w) != 0) return false; // 又回到自己了，且不为0if(vis[v]) continue;vis[v] = 1;if(!dfs(v, val ^ w, s)) return false;}return true;
}void solve()
{int n, m; cin >> n >> m;for(int i = 1; i <= m; i ++){int a, b, c; cin >> a >> b >> c;G[a].push_back({b, c}), G[b].push_back({a, c});}bool flag = true;for(int i = 1; i <= n; i ++){memset(vis, 0, sizeof vis);vis[i] = 1;flag &= dfs(i, 0, i);if(!flag) break;}cout << (flag? "Yes" : "No") << '\n';for(int i = 1; i <= n; i ++) G[i].clear(); // 清空！
}

当然也可以用什么带权并查集之类的做。（其实是我没调过）