题目描述

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：
输入：height = [4,2,0,3,2,5]
输出：9

提示：
n == height.length
1 <= n <= 2 * 104
0 <= height[i] <= 105

思考一（动态规划）

可能一开始琢磨着怎么统计连续的接水区域面积，想不到把柱子形成的洼地分解成一个个柱子宽度大小的单位水桶进行计算，如下图：

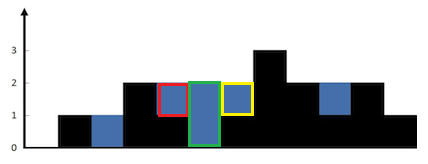
洼地分解成每个柱子宽度的水桶，只要确定这个水桶左右边界（木板）的高度最小值就能计算这个柱子的接水量了。比如图中的红色区域柱子，它的左边木板高度是 2，是左边所有柱子高度的最大值，这个木板高度为什么取左边最大值？显然，左边最高的木板能挡住更多的水，如果左边最高的木板离当前柱子比较远，那接水的面积可能更大。同理右边木板最大高度是右边所有柱子中高度最大的。现在确定了当前水桶（柱子）的左右木板高度，那么实际水桶的接水量就取决于两个木板最短的那个减去当前柱子的高度，即 $water[i]=Min(leftSide,rightSide)-height[i]$。上图中的红色部分接水量 $w=Math.min(2,3)-1=1$。定义两个数组 leftMax 和 rightMax 用于分别存储每个柱子左右木板的最大值，初始化 leftMax = height[0], rightMax = height[height.length-1]，分别正序遍历和倒序遍历数组更新leftMax[i] 和 rightMax[i]，每次遍历的高度与数组存储的之前最大高度比较取最大值，这是动态规划思想。最后遍历高度数组 height，根据预处理的当前柱子左右木板高度和当前柱子高度很容易计算当前柱子的接水量，累加所有柱子接水量就是整个题目的答案。

算法过程

1. 初始化两个数组 leftMax 和 rightMax，分别用于存储每个位置左侧和右侧的最大高度
2. 正序遍历高度数组，计算 leftMax[i]：每个位置左侧的最大高度（包含当前位置）
3. 倒序遍历高度数组，计算 rightMax[i]：每个位置右侧的最大高度（包含当前位置）
4. 遍历每个位置，计算该位置可接水量：Math.min(leftMax[i], rightMax[i]) - height[i]
5. 累加所有位置的接水量，得到总接水量并返回，时间复杂度$O(n)$，空间复杂度$O(n)$。

代码

/*** @param {number[]} height* @return {number}*/
var trap = function(height) {const len = height.length;const leftMax = new Array(height