2 损失函数

2.1 概述

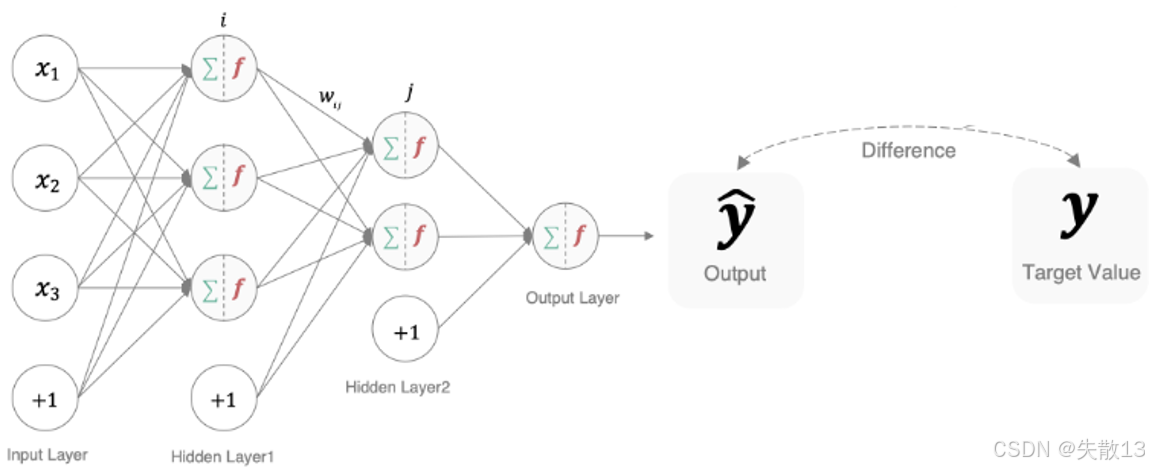
作用：衡量模型预测结果（ $y^\hat{y}$ ）和真实标签（ $y$ ）的差异，差异越大，说明模型参数“质量越差”（需要调整）；
本质：深度学习训练的“指挥棒”——反向传播时，损失函数的梯度会告诉模型“怎么调整参数，才能让预测更准”；
在不同文献/框架中，损失函数可能有这些名字：

2.2 多分类任务损失函数

2.2.1 概述

在多分类任务通常使用 softmax 将 logits（神经网络在经过最后一层线性变换后，尚未经过激活函数处理的原始输出值）转换为概率的形式，所以多分类的交叉熵损失也叫做 Softmax 损失
$\mathcal{L} = -\sum_{i=1}^{n} \mathbf{y}_i \log\left(S(f_\theta(\mathbf{x}_i))\right)$
- $yi\mathbf{y}_i$ ：真实标签的 one-hot 编码（比如二分类中，“猫”的标签是 [1, 0] ，“狗”是 [0, 1]）；
- $fθ(xi)f_\theta(\mathbf{x}_i)$ ：模型对样本 $xi\mathbf{x}_i$ 的“原始预测分数”（logits）；
- $S$ （Softmax 函数）：把 logits 转换成“概率分布”（所有类别概率和为 1）；
- $L\mathcal{L}$ ：损失值，衡量“预测概率分布”和“真实标签分布”的差异 → 差异越大，损失越大，模型越需要调整参数；
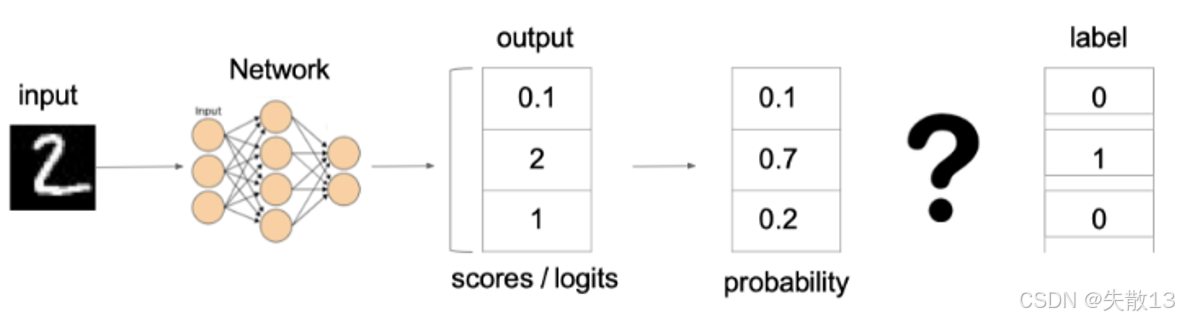
以“识别手写数字 2”为例：
- 模型输出：
  - logits（原始分数）：[0.1, 2, 1]（假设 3 分类，对应“0、1、2”）；
  - Softmax 转换后概率：[0.1, 0.7, 0.2]（和为 1 ，模型认为“是 1 的概率 70%”）；
- 真实标签：one-hot 编码为 [0, 1, 0]；
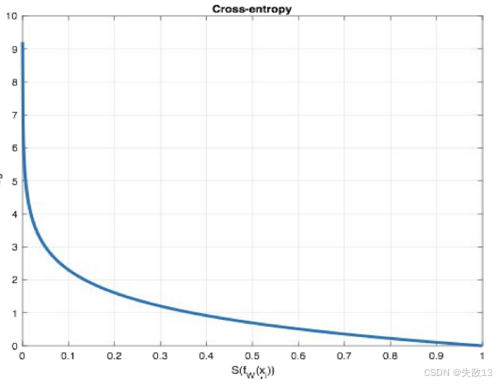
- 损失计算：代入公式，只有真实类别（“1”）的 $yi\mathbf{y}_i$ 是 1，其他是 0 → 损失简化为：
  $L=−(0log⁡(0.10)+1log⁡(0.7)+0log⁡(0.2))=−log⁡0.7\mathcal{L} = - \left( 0 \log(0.10) + 1 \log(0.7) + 0 \log(0.2) \right) = -\log 0.7$
  - 损失越小，说明预测概率越接近真实标签 → 训练时，模型会调整参数让这个损失“尽可能小”；
多分类交叉熵损失的意义：
- 对齐概率分布：让模型预测的“概率分布”尽可能贴近真实标签的“one-hot 分布”（比如真实是“猫”，就希望“猫”的概率趋近 1，其他趋近 0）；
- 反向传播的依据：损失值的梯度会告诉模型“怎么调整参数”，让预测更准；

2.2.2 代码

在 pytorch 中使用 nn.CrossEntropyLoss() 实现

import torch
import torch.nn as nn

# nn.CrossEntropyLoss()=softmax + 损失计算
# 说明：PyTorch中的CrossEntropyLoss会自动对输入的预测值先做softmax，再计算交叉熵损失
def test1():# 设置真实值：可以是热编码后的结果也可以不进行热编码。这里演示的是“不进行独热编码”的写法，直接用类别索引表示真实标签# 注意：真实标签的类型必须是64位整型数据（torch.int64）# 解释：y_true存储的是样本的真实类别索引，比如[1, 2]表示第1个样本属于类别1，第2个样本属于类别2y_true = torch.tensor([1, 2], dtype=torch.int64)# y_pred存储模型的预测结果，形状是[样本数, 类别数]# 解释：这里是2个样本，3个类别，每个样本输出3个预测概率（已经是softmax后的结果也可以直接是logits，CrossEntropyLoss会自动处理）# 示例中：# 第1个样本预测类别0概率0.2、类别1概率0.6、类别2概率0.2 # 第2个样本预测类别0概率0.1、类别1概率0.8、类别2概率0.1 y_pred = torch.tensor([[0.2, 0.6, 0.2], [0.1, 0.8, 0.1]], dtype=torch.float32)# 实例化交叉熵损失# 解释：创建CrossEntropyLoss对象，它会自动完成：# 1. 对y_pred做softmax（如果输入的是logits）# 2. 与y_true（类别索引）计算交叉熵损失loss = nn.CrossEntropyLoss()# 计算损失结果# 解释：将预测值y_pred和真实标签y_true传入loss函数，自动计算损失# .numpy()是为了把PyTorch的张量转换成numpy数组，方便打印查看my_loss = loss(y_pred, y_true).numpy()# 打印损失值print('loss:', my_loss)

在这里插入图片描述

2.2.3 输出结果分析

输入数据：
- 真实标签 y_true = [1, 2]：表示 2 个样本，第 1 个样本属于类别 1，第 2 个样本属于类别 2（类别索引从 0 开始）；
- 预测概率 y_pred = [[0.2, 0.6, 0.2], [0.1, 0.8, 0.1]]：
  - 第 1 个样本对 3 个类别的预测概率：类别0：0.2、类别1：0.6、类别2：0.2；
  - 第 2 个样本对 3 个类别的预测概率：类别0：0.1、类别1：0.8、类别2：0.1；
损失计算逻辑（CrossEntropyLoss）：CrossEntropyLoss 会自动对 y_pred 做 Softmax（如果输入的是 logits），然后计算交叉熵。公式简化为：
$\text{loss} = -\frac{1}{N} \sum_{i=1}^N \log\left( p_{\text{正确类别}} \right)$
- $ N $ 是样本数量（这里 $ N=2 $ ）；
- $ p_{\text{正确类别}} $ 是样本预测为“真实类别”的概率；
与2.2.1 概述中的公式本质是同一个损失逻辑，只是从 “简化版（针对类别索引）” 和 “完整版（针对 one-hot 编码）” 两个角度描述多分类交叉熵损失，核心逻辑完全一致；
逐样本计算
- 样本 1（真实类别 1）：预测为类别 1 的概率是 0.6 → 损失项：$ -\log(0.6) \approx 0.5108 $；
- 样本 2（真实类别 2）：预测为类别 2 的概率是 0.1 → 损失项：$ -\log(0.1) \approx 2.3026 $；
最终损失为两个样本的平均损失：
$\text{loss} = \frac{0.5108 + 2.3026}{2} \approx 1.4067$
但实际运行结果是 1.1200755，因为传入的 y_pred 实际上已经是概率（softmax后的输出），但CrossEntropyLoss再对它做softmax（logits -> softmax），这就导致计算不对，损失值偏小；
代码输出结果的含义：损失值 1.1200755 表示模型对这两个样本的预测“不够准确”，需要反向传播调整参数，让正确类别的预测概率更高。

2.3 二分类任务损失函数

2.3.1 概述

在处理二分类任务时，我们不再使用 softmax 激活函数，而是使用 sigmoid 激活函数，那损失函数也相应地进行调整，使用二分类的交叉熵损失函数（也叫二元交叉熵，Binary Cross-Entropy, BCE ）：
$L=−ylog⁡y^−(1−y)log⁡(1−y^) L = -y \log \hat{y} - (1 - y) \log(1 - \hat{y})$
- 适用任务：二分类（比如“垃圾邮件/正常邮件”“患病/健康”）；
- 激活函数：搭配 sigmoid 激活函数，让模型输出 $ \hat{y} $ 是“样本属于正类的概率”（范围 (0, 1)）；
- $ y $：样本的真实标签（二分类中，通常是 0 或 1 ，比如 1 代表“正类”，0 代表“负类”）；
- $ \hat{y} $：模型的预测概率（经过 sigmoid 后，是样本属于正类的概率）；
损失计算逻辑
- 如果样本是正类（$ y=1 $ ）：公式简化为 $ L = -\log \hat{y} $ → 预测概率 $ \hat{y} $ 越接近 1 ，损失越小；越接近 0 ，损失越大（惩罚模型“把正类预测成负类”）；
如果样本是负类（$ y=0 $ ）：公式简化为 $ L = -\log(1 - \hat{y}) $ → 预测概率 $ \hat{y} $ 越接近 0 ，损失越小；越接近 1 ，损失越大（惩罚模型“把负类预测成正类”）；
二元交叉熵的意义：
- 对齐概率：让模型预测的“正类概率”尽可能贴近真实标签（1 或 0 ）；
- 反向传播依据：训练时，损失的梯度会指导模型调整参数，让预测更准确（比如预测正类概率不够大，就调整参数让它变大）。

2.3.2 代码

在 pytorch 中使用nn.BCELoss()实现

def test2():# 设置真实值和预测值# 预测值是sigmoid输出的结果（已经过sigmoid归一化到0~1区间）# 解释：y_pred存储3个样本的预测概率，requires_grad=True表示需要计算梯度（用于反向传播）y_pred = torch.tensor([0.6901, 0.5459, 0.2469], requires_grad=True)# 真实标签：0表示负类，1表示正类，dtype=torch.float32是BCELoss的输入要求# 解释：y_true和y_pred长度必须一致，每个元素对应一个样本的真实类别（0/1）y_true = torch.tensor([0, 1, 0], dtype=torch.float32)# 实例化二分类交叉熵损失（BCE损失）# 解释：nn.BCELoss专门用于二分类任务，计算预测概率与真实标签的交叉熵criterion = nn.BCELoss()# 计算损失# 解释：将预测概率y_pred和真实标签y_true传入损失函数# .detach()是为了阻断反向传播（避免计算图占用内存），.numpy()转成numpy数组方便打印my_loss = criterion(y_pred, y_true).detach().numpy()# 打印最终损失值print('loss: ', my_loss)test2()

在这里插入图片描述

2.3.3 输出结果分析

输入数据
- 预测概率 y_pred = [0.6901, 0.5459, 0.2469]：3 个样本的预测概率（已经过 Sigmoid 归一化到 0~1）；
- 真实标签 y_true = [0, 1, 0]：3 个样本的真实类别，0 表示负类，1 表示正类；
损失计算逻辑（BCELoss）：BCELoss 用于二分类，公式为
$loss=−1N∑i=1N(yilog⁡(y^i)+(1−yi)log⁡(1−y^i)) \text{loss} = -\frac{1}{N} \sum_{i=1}^N \left( y_i \log(\hat{y}_i) + (1-y_i) \log(1-\hat{y}_i) \right)$
- $ y_i $ 是真实标签（0 或 1）
- $ \hat{y}_i $ 是预测概率
逐样本计算
- 样本 1（真实标签 0）：损失项：$ -(0 \cdot \log(0.6901) + 1 \cdot \log(1-0.6901)) = -\log(0.3099) \approx 1.173 $；
- 样本 2（真实标签 1）：损失项：$ -(1 \cdot \log(0.5459) + 0 \cdot \log(1-0.5459)) = -\log(0.5459) \approx 0.604 $；
- 样本 3（真实标签 0）：损失项：$ -(0 \cdot \log(0.2469) + 1 \cdot \log(1-0.2469)) = -\log(0.7531) \approx 0.283 $；
最终损失为平均 3 个样本的损失：
$\text{loss} = \frac{1.173 + 0.604 + 0.283}{3} \approx 0.6867$
代码输出结果的含义：损失值 0.6867941 表示模型对这 3 个样本的预测“不够准确”，需要反向传播调整参数，让正类样本的预测概率更高，负类样本的预测概率更低。

2.4 回归任务损失函数-MAE损失函数

2.4.1 概述

MAE（Mean Absolute Error，平均绝对误差）损失函数，也叫 L1 Loss，，是以绝对误差作为距离。公式：
$\mathcal{L} = \frac{1}{n} \sum_{i=1}^{n} \left| y_i - f_\theta(x_i) \right|$
- $ y_i $：样本的真实值；
- $ f_\theta(x_i) $：模型对样本 $ x_i $ 的预测值；
- $ n $：样本数量；
- $ \mathcal{L} $：损失值，衡量“预测值与真实值的绝对误差的平均值” → 误差越大，损失越大，模型越需要调整参数；
特点：
- 稀疏性（正则化效果）：MAE 对“大误差”更敏感（因为是绝对值，大误差不会被“平方缩小”），会惩罚模型预测偏差大的情况。因此常被用作“正则项”，约束模型参数，避免过拟合；
- 梯度不光滑问题：在预测值 = 真实值（误差为 0）时，绝对值函数的梯度不连续（左右导数突变）。训练时，梯度下降可能“跳过极小值点”，导致模型收敛到次优解；
图像：
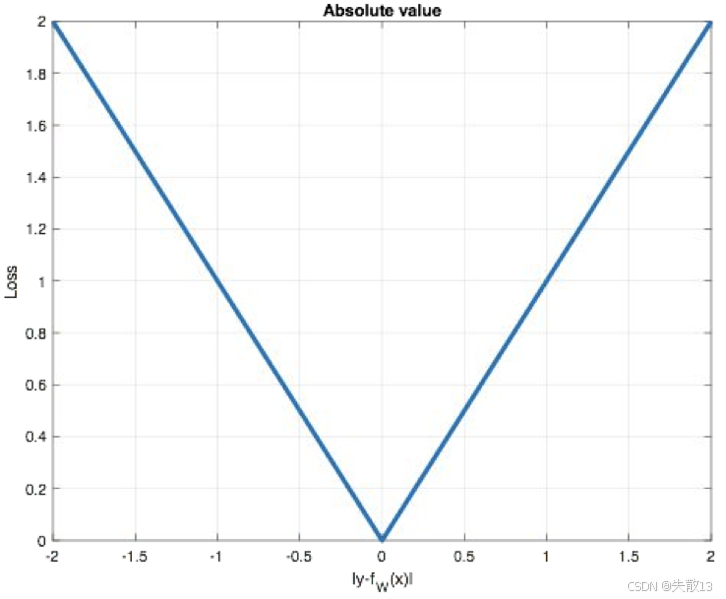
- 横轴：预测误差（$ |y_i - f_\theta(x_i)| $ ）；纵轴：损失值（$ \mathcal{L} $ ）；
- 图像是“V 型”，体现 MAE 的特点：
  - 误差越大，损失线性增长（惩罚大误差）；
  - 误差为 0 时，损失最小（模型预测完全准确）。

2.4.2 代码

在 pytorch 中使用 nn.L1Loss() 实现：

# 定义测试函数，演示 MAE（L1 Loss）的计算流程
def test3():# 设置预测值和真实值# y_pred：模型的预测结果，需要计算梯度（requires_grad=True）用于反向传播# 这里是 3 个样本的预测值：[1.0, 1.0, 1.9]y_pred = torch.tensor([1.0, 1.0, 1.9], requires_grad=True)# y_true：样本的真实标签，dtype=torch.float32 是 L1Loss 的输入要求# 这里是 3 个样本的真实值：[2.0, 2.0, 2.0]y_true = torch.tensor([2.0, 2.0, 2.0], dtype=torch.float32)# 实例化 MAE 损失函数（L1 Loss）# nn.L1Loss 会计算预测值与真实值的绝对误差的平均值criterion = nn.L1Loss()# 计算损失# 将预测值 y_pred 和真实值 y_true 传入损失函数，自动计算 MAE# .detach() 用于切断反向传播（避免保留计算图占用内存）# .numpy() 转成 numpy 数组，方便打印查看结果my_loss = criterion(y_pred, y_true).detach().numpy()# 打印最终损失值print('loss:', my_loss)
test3()

在这里插入图片描述

2.4.3 输出结果分析

MAE 损失函数的计算公式为：
$\text{MAE} = \frac{1}{n} \sum_{i=1}^{n} \left| y_{\text{pred},i} - y_{\text{true},i} \right|$
- 其中：
  - $ n $ 是样本数量（这里 $ n = 3 $ ，对应 3 个预测值和 3 个真实值）；
  - $ y_{\text{pred},i} $ 是模型对第 $ i $ 个样本的预测值；
  - $ y_{\text{true},i} $ 是第 $ i $ 个样本的真实标签值；
代码中给出的预测值和真实值分别是：
- 预测值 $ y_{\text{pred}} = [1.0, 1.0, 1.9] $
- 真实值 $ y_{\text{true}} = [2.0, 2.0, 2.0] $
逐样本计算绝对误差，再求平均：
1. 第 1 个样本绝对误差：$ |1.0 - 2.0| = 1.0 $
2. 第 2 个样本绝对误差：$ |1.0 - 2.0| = 1.0 $
3. 第 3 个样本绝对误差：$ |1.9 - 2.0| = 0.1 $
将这些绝对误差求平均：
$\text{MAE} = \frac{1.0 + 1.0 + 0.1}{3} = \frac{2.1}{3} = 0.7$
代码输出结果的含义：
- 最终输出 loss: 0.7 ，表示模型预测值与真实值的平均绝对误差是 0.7；
- 损失值越小，说明模型预测越接近真实标签；损失值越大，说明预测偏差越大，需要继续调整模型参数（如通过反向传播优化网络权重）来减小误差。

2.5 回归任务损失函数-MSE损失函数

2.5.1 概述

MSE（均方误差，Mean Squared Error）损失函数，也叫 L2 Loss 或欧氏距离，它以误差的平方和的均值作为距离。公式：
$\mathcal{L} = \frac{1}{n} \sum_{i=1}^{n} \left( y_i - f_\theta(x_i) \right)^2$
- $ y_i $：样本的真实值（比如实际房价）；
- $ f_\theta(x_i) $：模型对样本 $ x_i $ 的预测值（比如模型预测的房价）；
- $ n $：样本数量；
- $ \mathcal{L} $：损失值，衡量“预测值与真实值的平方误差的平均值” → 误差越大，损失越大，模型越需要调整参数；
特点：
- 作为正则项（L2 正则）：MSE 的“平方”特性，会放大模型的“大误差”（比如预测偏差 2 → 平方后是 4 ，偏差 3 → 平方后是 9）。这种“惩罚大误差”的特点，让 MSE 常被用作正则项（比如 L2 正则），约束模型参数不要过大，避免过拟合；
- 梯度爆炸风险：当预测值与真实值偏差很大时（比如模型预测房价 100 万，实际是 1000 万），平方误差会非常大（$ (1000-100)^2 = 810000 $）。反向传播时，梯度（损失对参数的导数）也会被“平方放大”，可能导致梯度爆炸（梯度值瞬间变得极大，模型参数更新幅度过大，无法稳定训练）；
图像：
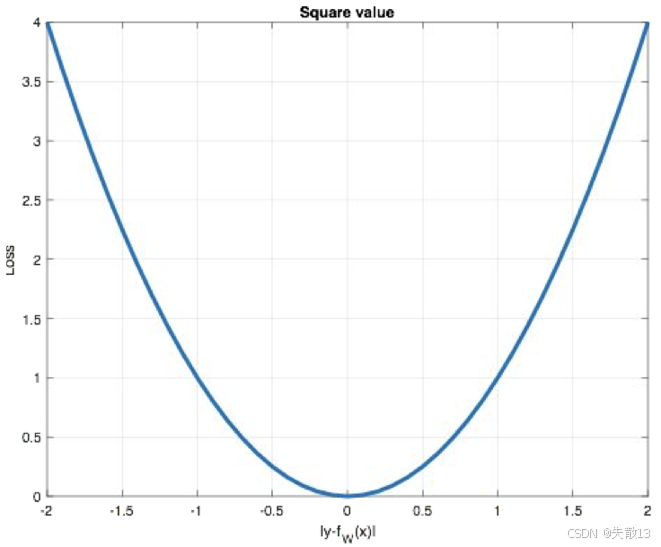
- 横轴：预测误差（$ y_i - f_\theta(x_i) $ ），纵轴：损失值（$ \mathcal{L} $ ）；
- 曲线是“U 型”，体现 MSE 的特点：
  - 误差越大，损失指数级增长（平方放大误差）；
  - 误差为 0 时，损失最小（模型预测完全准确）；
适合场景：数据分布较均匀、无极端异常值，且希望模型对“小误差更敏感”的回归任务（比如预测温度，误差 1℃ 影响大，需要重点优化）；
对比 MAE（L1 Loss）：
- MAE 对异常值鲁棒（绝对值不放大误差），但梯度在 0 点不连续（训练可能不稳定）；
- MSE 对异常值更敏感（平方放大误差），但梯度光滑（训练更稳定）。

2.5.2 代码

在 pytorch 中使用 nn.MSELoss() 实现

def test4():# 准备预测值和真实值# y_pred: 模型输出的预测结果，需要计算梯度(requires_grad=True)用于反向传播更新参数# 这里模拟 3 个样本的预测值: [1.0, 1.0, 1.9]y_pred = torch.tensor([1.0, 1.0, 1.9], requires_grad=True)# y_true: 样本的真实标签，dtype=torch.float32 是 MSELoss 要求的输入类型# 这里模拟 3 个样本的真实值: [2.0, 2.0, 2.0]y_true = torch.tensor([2.0, 2.0, 2.0], dtype=torch.float32)# 初始化 MSE 损失函数# nn.MSELoss 会计算预测值与真实值的均方误差（平方误差的平均值）loss_function = nn.MSELoss()# 计算损失值# 将预测值和真实值传入损失函数，自动执行: # 1) 逐样本计算 (y_pred - y_true)^2 # 2) 对所有样本的平方误差求平均# .detach() 用于切断反向传播链路（避免保存计算图占用内存）# .numpy() 转换为 numpy 数组方便打印查看calculated_loss = loss_function(y_pred, y_true).detach().numpy()# 打印最终损失结果print('loss:', calculated_loss)
test4()

在这里插入图片描述

2.5.3 输出结果分析

MSE 损失函数的公式：
$\text{MSE} = \frac{1}{n} \sum_{i=1}^{n} \left( y_{\text{pred},i} - y_{\text{true},i} \right)^2$
- $ n $：样本数量（这里 $ n = 3 $ ，3 个样本）；
- $ y_{\text{pred},i} $：模型对第 $ i $ 个样本的预测值；
- $ y_{\text{true},i} $：第 $ i $ 个样本的真实值；
代码中，预测值和真实值分别为：
- 预测值 $ y_{\text{pred}} = [1.0, 1.0, 1.9] $
- 真实值 $ y_{\text{true}} = [2.0, 2.0, 2.0] $
对每个样本，计算“预测值 - 真实值”的平方：
- 样本 1：$ (1.0 - 2.0)^2 = (-1.0)^2 = 1.0 $
- 样本 2：$ (1.0 - 2.0)^2 = (-1.0)^2 = 1.0 $
- 样本 3：$ (1.9 - 2.0)^2 = (-0.1)^2 = 0.01 $
计算“平均平方误差”：将所有样本的平方误差求和，再除以样本数量 $ n = 3 $：
$\text{MSE} = \frac{1.0 + 1.0 + 0.01}{3} = \frac{2.01}{3} = 0.67$
代码输出结果的含义：
- 输出 loss: 0.67 表示模型预测值与真实值的均方误差是 0.67；
- 损失值越小，说明模型预测越接近真实标签；损失值越大，说明预测偏差越大，需要继续调整模型参数（如通过反向传播优化网络权重）来减小误差；
MSE 的特点（结合代码场景）
- 放大“大误差”：MSE 对“大误差”更敏感（平方会放大误差）。如果模型预测偏差大（比如样本 1、2 的偏差是 1.0），平方后会让损失更显著，推动模型优先优化这些“大误差”；
- 梯度更新特性：MSE 的梯度（损失对模型参数的导数）与“预测误差”成正比（梯度 = $ 2 \times (y_{\text{pred}} - y_{\text{true}}) $）。误差越大，梯度越大，模型参数更新幅度也越大，这可能导致“梯度爆炸”（但本示例误差小，无此问题）。

2.6 回归任务损失函数-smooth L1损失函数

2.6.1 概述

Smooth L1 是分段函数，定义：
$\text{smooth}_{L_1}(x) = \begin{cases} 0.5x^2 & \text{如果 } |x| < 1 \\ |x| - 0.5 & \text{否则} \end{cases}$
- $x$ ：预测值与真实值的误差（$ x = f(x) - y $ ，即模型预测偏差）；
设计目的（解决 L1/L2 的缺点）
损失函数缺点 Smooth L1 的改进逻辑
L1（MAE）误差为 0 时梯度不连续（影响训练稳定性）当 $
L2（MSE）误差大时梯度爆炸（异常值敏感）当 $
图像：
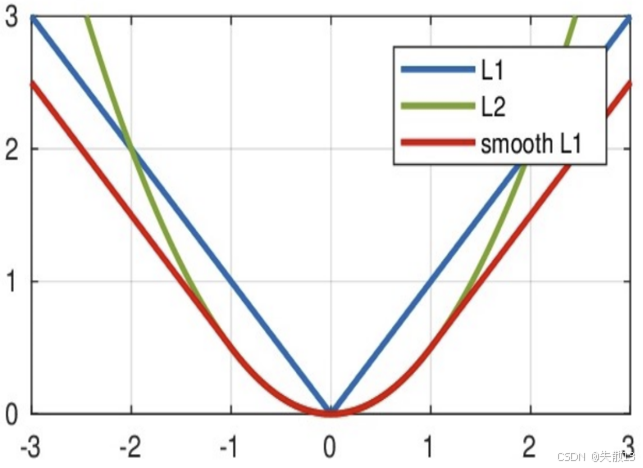
- L1（蓝色）：V 型，误差大时梯度稳定，但 0 点不光滑；
- L2（绿色）：U 型，误差小时梯度光滑，但误差大时梯度爆炸；
- Smooth L1（红色）：
  - 误差小（$ |x| < 1 $ ）：曲线和 L2 重合（梯度光滑）；
  - 误差大（$ |x| \geq 1 $ ）：曲线和 L1 重合（梯度稳定，避免爆炸）；
Smooth L1 结合了 L1 和 L2 的优点，适合：回归任务中存在异常值（需要 L1 的鲁棒性），但希望训练更稳定（需要 L2 的光滑梯度）的场景（比如目标检测中的边界框回归）。

损失函数	缺点	Smooth L1 的改进逻辑
L1（MAE）	误差为 0 时梯度不连续（影响训练稳定性）	当 $
L2（MSE）	误差大时梯度爆炸（异常值敏感）	当 $

2.6.2 代码

在 pytorch 中使用nn.SmoothL1Loss()实现：

def test5():# 准备预测值和真实值# y_true: 样本的真实标签，这里是 [0, 3]（2个样本的真实值）y_true = torch.tensor([0, 3])# y_pred: 模型的预测结果，需要计算梯度(requires_grad=True)用于反向传播# 这里是 2 个样本的预测值: [0.6, 0.4]y_pred = torch.tensor([0.6, 0.4], requires_grad=True)# 初始化 Smooth L1 损失函数# nn.SmoothL1Loss 会根据预测误差的大小，自动切换 L1/L2 损失逻辑：# - 误差小（|x| < 1）: 用 L2 损失 (0.5x²)# - 误差大（|x| ≥ 1）: 用 L1 损失 (|x| - 0.5)criterion = nn.SmoothL1Loss()# 3. 计算损失值# 逐样本计算误差 x = y_pred - y_true，再代入 Smooth L1 公式# .detach() 切断反向传播（避免保存计算图占用内存）# .numpy() 转成 numpy 数组方便打印calculated_loss = criterion(y_pred, y_true).detach().numpy()# 打印最终损失print('loss:', calculated_loss)
test5()

在这里插入图片描述

2.6.3 输出结果分析

Smooth L1 是分段函数，公式：
$\text{smooth}_{L_1}(x) = \begin{cases} 0.5x^2 & \text{如果 } |x| < 1 \text{（误差小，用 L2 损失）} \\ |x| - 0.5 & \text{如果 } |x| \geq 1 \text{（误差大，用 L1 损失）} \end{cases}$
- 其中，$ x = y_{\text{pred}} - y_{\text{true}} $（预测值与真实值的误差）；
代码中，预测值和真实值分别为：
- 预测值 $ y_{\text{pred}} = [0.6, 0.4] $
- 真实值 $ y_{\text{true}} = [0, 3] $
对每个样本，计算 $ x = y_{\text{pred}} - y_{\text{true}} $：
- 样本 1：$ x_1 = 0.6 - 0 = 0.6 $
- 样本 2：$ x_2 = 0.4 - 3 = -2.6 $
分段计算“样本损失”，根据 Smooth L1 的分段逻辑：
- 样本 1（$ |x_1| = 0.6 < 1 $，误差小 → 用 L2 损失）
  $\text{损失}_1 = 0.5 \times (0.6)^2 = 0.5 \times 0.36 = 0.18$
- 样本 2（$ |x_2| = 2.6 \geq 1 $，误差大 → 用 L1 损失）
  $\text{损失}_2 = |-2.6| - 0.5 = 2.6 - 0.5 = 2.1$
Smooth L1 损失默认返回所有样本损失的平均值：

$\text{总损失} = \frac{\text{损失}_1 + \text{损失}_2}{2} = \frac{0.18 + 2.1}{2} = \frac{2.28}{2} = 1.14$
代码输出结果的含义：
- 输出 loss: 1.14 表示：模型预测值与真实值的Smooth L1 损失是 1.14；
- 损失值综合了“误差小样本的 L2 平滑”和“误差大样本的 L1 鲁棒性”，既避免了 L2 对异常值的敏感，又解决了 L1 在误差为 0 时的梯度不连续问题，让模型训练更稳定。