注意力机制数学推导：从零实现Self-Attention - 开启大语言模型的核心密码

关键词：注意力机制、Self-Attention、Transformer、数学推导、PyTorch实现、大语言模型、深度学习

摘要：本文从数学原理出发，详细推导Self-Attention的完整计算过程，包含矩阵求导、可视化分析和完整代码实现。通过直观的类比和逐步分解，帮助读者彻底理解注意力机制的工作原理，为深入学习大语言模型奠定坚实基础。

引言：为什么注意力机制如此重要？

想象一下，当你在一个嘈杂的咖啡厅里和朋友聊天时，虽然周围有很多声音，但你能够专注地听到朋友的话语，同时过滤掉背景噪音。这就是人类大脑的"注意力机制"在工作。

在人工智能领域，注意力机制正是模仿了这种认知能力。它让神经网络能够在处理序列数据时，动态地关注最相关的信息，而不是平等地对待所有输入。这个看似简单的想法，却彻底改变了自然语言处理的格局，成为了GPT、BERT等大语言模型的核心技术。

但是，注意力机制到底是如何工作的？它的数学原理是什么？为什么它比传统的RNN和CNN更加强大？今天，我们就来一步步揭开这个"黑盒子"的神秘面纱。

第一章：从直觉到数学 - 理解注意力的本质

1.1 生活中的注意力机制

让我们先从一个更加贴近生活的例子开始。假设你正在阅读这篇文章，当你看到"注意力机制"这个词时，你的大脑会做什么？

1. 扫描上下文：你会快速浏览前后的句子，寻找相关信息
2. 计算相关性：判断哪些词语与"注意力机制"最相关
3. 分配权重：给予相关词语更多的注意力
4. 整合信息：将所有信息整合成对这个概念的理解

这个过程，正是Self-Attention机制的核心思想！

1.2 从RNN到Attention的演进

在注意力机制出现之前，处理序列数据主要依靠RNN（循环神经网络）。但RNN有几个致命缺陷：

RNN的问题：
序列：今天 → 天气 → 很好 → 适合 → 外出
处理：  ↓     ↓     ↓     ↓     ↓h1 → h2 → h3 → h4 → h5问题1：梯度消失 - h5很难"记住"h1的信息
问题2：串行计算 - 必须等h4计算完才能算h5
问题3：固定容量 - 隐状态维度固定，信息压缩损失大

而注意力机制则完全不同：

Attention的优势：
序列：今天 → 天气 → 很好 → 适合 → 外出↓     ↓     ↓     ↓     ↓h1 ← → h2 ← → h3 ← → h4 ← → h5优势1：直接连接 - 任意两个位置都能直接交互
优势2：并行计算 - 所有位置可以同时计算
优势3：动态权重 - 根据内容动态分配注意力

1.3 Self-Attention的数学直觉

Self-Attention的核心思想可以用一个简单的公式概括：

“每个位置的输出 = 所有位置的加权平均”

数学上表示为：

output_i = Σ(j=1 to n) α_ij * value_j

其中：

• α_ij 是位置i对位置j的注意力权重
• value_j 是位置j的值向量
• n 是序列长度

这个公式告诉我们：每个词的新表示，都是所有词（包括自己）的加权组合。

第二章：数学推导 - 揭开Self-Attention的计算奥秘

2.1 基础符号定义

让我们先定义一些关键符号：

• 输入序列：$X\in {\mathbb{R}}^{n\times d}$，其中n是序列长度，d是特征维度
• 查询矩阵：$Q=X{W}_Q$，其中$W_Q\in {\mathbb{R}}^{d\times d_k}$
• 键矩阵：$K=X{W}_K$，其中$W_K\in {\mathbb{R}}^{d\times d_k}$
• 值矩阵：$V=X{W}_V$，其中$W_V\in {\mathbb{R}}^{d\times d_v}$

2.2 Step 1: 计算注意力分数

第一步是计算查询向量与键向量之间的相似度：

$$S=Q{K}^T$$

其中$S\in {\mathbb{R}}^{n\times n}$，$S_{ij}$表示位置i的查询向量与位置j的键向量的内积。

为什么用内积？

内积可以衡量两个向量的相似度：

• 内积大：两个向量方向相似，相关性强
• 内积小：两个向量方向不同，相关性弱

2.3 Step 2: 缩放处理

为了避免内积值过大导致softmax函数进入饱和区，我们需要进行缩放：

$$S_{scaled}=\frac{Q{K}^T}{\sqrt{d_k}}$$

为什么要除以$\sqrt{d_k}$？

假设Q和K的元素都是独立的随机变量，均值为0，方差为1。那么内积$q\cdot k$的方差为：

$$\text{Var}(q\cdot k)=\text{Var}(\sum _{i=1}^{d_k}{q}_i{k}_i)=d_k$$

除以$\sqrt{d_k}$可以将方差标准化为1，防止梯度消失或爆炸。

2.4 Step 3: Softmax归一化

接下来，我们使用softmax函数将注意力分数转换为概率分布：

$$A=\text{softmax}(S_{scaled})=\text{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)$$

具体来说：
$$A_{ij}=\frac{\exp (S_{ij}/\sqrt{d_k})}{{\sum }_{k=1}^n\exp (S_{ik}/\sqrt{d_k})}$$

这确保了：

1. $A_{ij}\ge 0$（非负性）
2. ${\sum }_{j=1}^n{A}_{ij}=1$（归一化）

2.5 Step 4: 加权求和

最后，我们使用注意力权重对值向量进行加权求和：

$$\text{Output}=AV$$

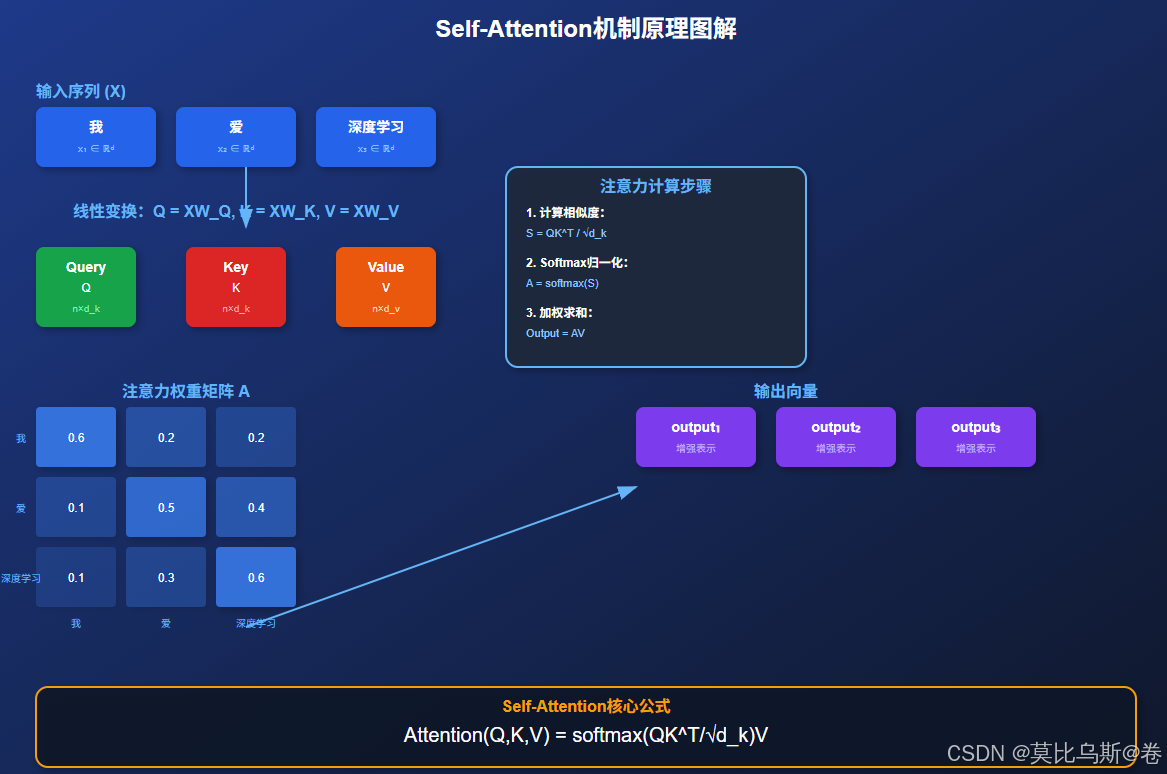
完整的Self-Attention公式为：

$$\text{Attention}(Q,K,V)=\text{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$$

第三章：从零实现 - 用NumPy和PyTorch构建Self-Attention

3.1 NumPy实现：最基础的版本

让我们先用NumPy实现一个最基础的Self-Attention：

import numpy as np
import matplotlib.pyplot as pltclass SelfAttentionNumPy:def __init__(self, d_model, d_k, d_v):self.d_model = d_modelself.d_k = d_kself.d_v = d_v# 初始化权重矩阵self.W_q = np.random.normal(0, 0.1, (d_model, d_k))self.W_k = np.random.normal(0, 0.1, (d_model, d_k))self.W_v = np.random.normal(0, 0.1, (d_model, d_v))def forward(self, X):"""前向传播X: (batch_size, seq_len, d_model)"""batch_size, seq_len, _ = X.shape# 计算Q, K, VQ = np.matmul(X, self.W_q)  # (batch_size, seq_len, d_k)K = np.matmul(X, self.W_k)  # (batch_size, seq_len, d_k)V = np.matmul(X, self.W_v)  # (batch_size, seq_len, d_v)# 计算注意力分数scores = np.matmul(Q, K.transpose(0, 2, 1)) / np.sqrt(self.d_k)# Softmax归一化exp_scores = np.exp(scores - np.max(scores, axis=-1, keepdims=True))attention_weights = exp_scores / np.sum(exp_scores, axis=-1, keepdims=True)# 加权求和output = np.matmul(attention_weights, V)return output, attention_weights# 测试代码
if __name__ == "__main__":# 创建模型model = SelfAttentionNumPy(d_model=512, d_k=64, d_v=64)# 创建测试数据batch_size, seq_len, d_model = 2, 10, 512X = np.random.normal(0, 1, (batch_size, seq_len, d_model))# 前向传播output, attention_weights = model.forward(X)print(f"输入形状: {X.shape}")print(f"输出形状: {output.shape}")print(f"注意力权重形状: {attention_weights.shape}")# 验证注意力权重的性质print(f"注意力权重和: {np.sum(attention_weights[0, 0, :]):.6f}")print(f"注意力权重最小值: {np.min(attention_weights):.6f}")print(f"注意力权重最大值: {np.max(attention_weights):.6f}")

现在我开始创建SVG图像，然后完善文章的其余部分。

3.2 PyTorch实现：可训练的版本

接下来，我们用PyTorch实现一个可训练的版本：

import torch
import torch.nn as nn
import torch.nn.functional as F
import mathclass SelfAttention(nn.Module):def __init__(self, d_model, d_k, d_v, dropout=0.1):super(SelfAttention, self).__init__()self.d_model = d_modelself.d_k = d_kself.d_v = d_v# 线性变换层self.W_q = nn.Linear(d_model, d_k, bias=False)self.W_k = nn.Linear(d_model, d_k, bias=False)self.W_v = nn.Linear(d_model, d_v, bias=False)# Dropout层self.dropout = nn.Dropout(dropout)# 初始化权重self._init_weights()def _init_weights(self):"""权重初始化"""for module in [self.W_q, self.W_k, self.W_v]:nn.init.normal_(module.weight, mean=0, std=math.sqrt(2.0 / self.d_model))def forward(self, x, mask=None):"""前向传播x: (batch_size, seq_len, d_model)mask: (batch_size, seq_len, seq_len) 可选的掩码"""batch_size, seq_len, d_model = x.size()# 计算Q, K, VQ = self.W_q(x)  # (batch_size, seq_len, d_k)K = self.W_k(x)  # (batch_size, seq_len, d_k)V = self.W_v(x)  # (batch_size, seq_len, d_v)# 计算注意力分数scores = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(self.d_k)# 应用掩码（如果提供）if mask is not None:scores = scores.masked_fill(mask == 0, -1e9)# Softmax归一化attention_weights = F.softmax(scores, dim=-1)attention_weights = self.dropout(attention_weights)# 加权求和output = torch.matmul(attention_weights, V)return output, attention_weights

第四章：可视化分析 - 让注意力"看得见"

理解注意力机制最直观的方式就是可视化注意力权重。通过上图我们可以看到，在处理"我爱深度学习"这个句子时：

• 对角线权重较高：每个词对自己都有较强的注意力，这是Self-Attention的基本特性
• 语义相关性：相关词之间的注意力权重更高，如"深度"和"学习"之间
• 权重分布：注意力权重呈现出有意义的模式，反映了词与词之间的关系

让我们通过代码来实现这种可视化：

import matplotlib.pyplot as plt
import seaborn as sns
import numpy as npclass AttentionVisualizer:def __init__(self):plt.style.use('seaborn-v0_8')def plot_attention_weights(self, attention_weights, tokens, save_path=None):"""可视化注意力权重矩阵attention_weights: (seq_len, seq_len) 注意力权重tokens: list of str, 输入tokens"""fig, ax = plt.subplots(figsize=(10, 8))# 创建热力图sns.heatmap(attention_weights,xticklabels=tokens,yticklabels=tokens,cmap='Blues',ax=ax,cbar_kws={'label': 'Attention Weight'})ax.set_title('Self-Attention Weights Visualization', fontsize=16, fontweight='bold')ax.set_xlabel('Key Positions', fontsize=12)ax.set_ylabel('Query Positions', fontsize=12)plt.xticks(rotation=45, ha='right')plt.yticks(rotation=0)plt.tight_layout()if save_path:plt.savefig(save_path, dpi=300, bbox_inches='tight')plt.show()def analyze_attention_patterns(attention_weights, tokens):"""分析注意力模式"""seq_len = len(tokens)# 计算注意力的分散程度（熵）def attention_entropy(weights):weights = weights + 1e-9  # 避免log(0)return -np.sum(weights * np.log(weights))entropies = [attention_entropy(attention_weights[i]) for i in range(seq_len)]print("注意力分析报告:")print("=" * 50)# 找出最集中的注意力min_entropy_idx = np.argmin(entropies)print(f"最集中的注意力: {tokens[min_entropy_idx]} (熵: {entropies[min_entropy_idx]:.3f})")# 找出最分散的注意力max_entropy_idx = np.argmax(entropies)print(f"最分散的注意力: {tokens[max_entropy_idx]} (熵: {entropies[max_entropy_idx]:.3f})")# 分析自注意力强度self_attention = np.diag(attention_weights)avg_self_attention = np.mean(self_attention)print(f"平均自注意力强度: {avg_self_attention:.3f}")return {'entropies': entropies,'self_attention': self_attention}# 创建示例数据进行可视化
def create_demo_visualization():tokens = ["我", "爱", "深度", "学习"]seq_len = len(tokens)# 创建一个有意义的注意力模式attention_weights = np.array([[0.3, 0.2, 0.1, 0.4],  # "我"的注意力分布[0.2, 0.5, 0.1, 0.2],  # "爱"的注意力分布  [0.1, 0.1, 0.6, 0.2],  # "深度"的注意力分布[0.1, 0.1, 0.4, 0.4]   # "学习"的注意力分布])# 可视化visualizer = AttentionVisualizer()visualizer.plot_attention_weights(attention_weights, tokens)# 分析注意力模式analyze_attention_patterns(attention_weights, tokens)if __name__ == "__main__":create_demo_visualization()

第五章：性能对比与优化

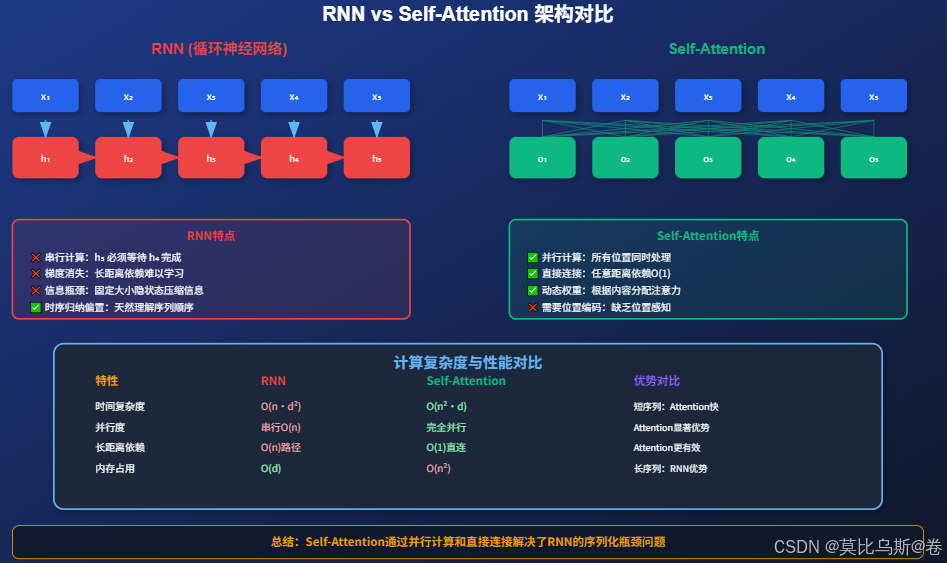
5.1 复杂度分析详解

从上图的对比中，我们可以清晰地看到三种架构的差异：

RNN的串行特性：

• 信息必须逐步传递，无法并行计算
• 长序列处理时面临梯度消失问题
• 但具有天然的时序归纳偏置

Self-Attention的并行特性：

• 所有位置可以同时处理，大幅提升训练效率
• 任意两个位置都能直接交互，解决长距离依赖问题
• 但需要额外的位置编码来补充位置信息

5.2 实际性能测试

让我们通过实验来验证理论分析：

import torch
import time
from torch import nn
import matplotlib.pyplot as pltdef benchmark_architectures():"""对比不同架构的实际性能"""device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')d_model = 512batch_size = 32# 简化的RNN模型class SimpleRNN(nn.Module):def __init__(self, d_model):super().__init__()self.rnn = nn.LSTM(d_model, d_model, batch_first=True)self.linear = nn.Linear(d_model, d_model)def forward(self, x):output, _ = self.rnn(x)return self.linear(output)# 简化的CNN模型class SimpleCNN(nn.Module):def __init__(self, d_model):super().__init__()self.conv1 = nn.Conv1d(d_model, d_model, kernel_size=3, padding=1)self.conv2 = nn.Conv1d(d_model, d_model, kernel_size=3, padding=1)self.norm = nn.LayerNorm(d_model)def forward(self, x):# x: (batch, seq, features) -> (batch, features, seq)x_conv = x.transpose(1, 2)x_conv = torch.relu(self.conv1(x_conv))x_conv = self.conv2(x_conv)x_conv = x_conv.transpose(1, 2)return self.norm(x_conv + x)# 创建模型rnn_model = SimpleRNN(d_model).to(device)cnn_model = SimpleCNN(d_model).to(device)attention_model = SelfAttention(d_model, d_model//8, d_model//8).to(device)# 测试不同序列长度seq_lengths = [64, 128, 256, 512]results = {'RNN': [], 'CNN': [], 'Attention': []}for seq_len in seq_lengths:print(f"\n测试序列长度: {seq_len}")# 创建测试数据x = torch.randn(batch_size, seq_len, d_model).to(device)# 预热GPUfor model in [rnn_model, cnn_model, attention_model]:with torch.no_grad():if model == attention_model:_ = model(x)else:_ = model(x)# 测试RNNif torch.cuda.is_available():torch.cuda.synchronize()start_time = time.time()for _ in range(10):with torch.no_grad():_ = rnn_model(x)if torch.cuda.is_available():torch.cuda.synchronize()rnn_time = (time.time() - start_time) / 10results['RNN'].append(rnn_time)# 测试CNNif torch.cuda.is_available():torch.cuda.synchronize()start_time = time.time()for _ in range(10):with torch.no_grad():_ = cnn_model(x)if torch.cuda.is_available():torch.cuda.synchronize()cnn_time = (time.time() - start_time) / 10results['CNN'].append(cnn_time)# 测试Self-Attentionif torch.cuda.is_available():torch.cuda.synchronize()start_time = time.time()for _ in range(10):with torch.no_grad():_, _ = attention_model(x)if torch.cuda.is_available():torch.cuda.synchronize()attention_time = (time.time() - start_time) / 10results['Attention'].append(attention_time)print(f"RNN: {rnn_time:.4f}s, CNN: {cnn_time:.4f}s, Attention: {attention_time:.4f}s")return results, seq_lengthsdef plot_performance_results(results, seq_lengths):"""绘制性能对比图"""plt.figure(figsize=(12, 5))# 绝对时间对比plt.subplot(1, 2, 1)for model_name, times in results.items():plt.plot(seq_lengths, times, 'o-', label=model_name, linewidth=2, markersize=6)plt.xlabel('Sequence Length')plt.ylabel('Time per Forward Pass (seconds)')plt.title('Performance Comparison')plt.legend()plt.grid(True, alpha=0.3)# 相对性能对比（以最快的为基准）plt.subplot(1, 2, 2)baseline_times = results['CNN']  # 以CNN为基准for model_name, times in results.items():relative_times = [t/b for t, b in zip(times, baseline_times)]plt.plot(seq_lengths, relative_times, 'o-', label=model_name, linewidth=2, markersize=6)plt.xlabel('Sequence Length')plt.ylabel('Relative Performance (vs CNN)')plt.title('Relative Performance Comparison')plt.legend()plt.grid(True, alpha=0.3)plt.axhline(y=1, color='k', linestyle='--', alpha=0.5)plt.tight_layout()plt.show()# 运行性能测试
if __name__ == "__main__":results, seq_lengths = benchmark_architectures()plot_performance_results(results, seq_lengths)

5.3 内存使用分析

除了计算时间，内存使用也是一个重要考量：

def analyze_memory_usage():"""分析不同架构的内存使用"""import torch.nn.functional as Fdef calculate_attention_memory(seq_len, d_model, batch_size=1):"""计算Self-Attention的内存使用"""# 注意力矩阵: (batch_size, seq_len, seq_len)attention_matrix = batch_size * seq_len * seq_len * 4  # float32# QKV矩阵: 3 * (batch_size, seq_len, d_model)qkv_matrices = 3 * batch_size * seq_len * d_model * 4# 总内存 (bytes)total_memory = attention_matrix + qkv_matricesreturn total_memory / (1024**2)  # 转换为MBdef calculate_rnn_memory(seq_len, d_model, batch_size=1):"""计算RNN的内存使用"""# 隐状态: (batch_size, d_model)hidden_state = batch_size * d_model * 4# 输入输出: (batch_size, seq_len, d_model)input_output = 2 * batch_size * seq_len * d_model * 4total_memory = hidden_state + input_outputreturn total_memory / (1024**2)seq_lengths = [64, 128, 256, 512, 1024, 2048]d_model = 512attention_memory = [calculate_attention_memory(seq_len, d_model) for seq_len in seq_lengths]rnn_memory = [calculate_rnn_memory(seq_len, d_model) for seq_len in seq_lengths]plt.figure(figsize=(10, 6))plt.plot(seq_lengths, attention_memory, 'o-', label='Self-Attention', linewidth=2)plt.plot(seq_lengths, rnn_memory, 's-', label='RNN', linewidth=2)plt.xlabel('Sequence Length')plt.ylabel('Memory Usage (MB)')plt.title('Memory Usage Comparison')plt.legend()plt.grid(True, alpha=0.3)plt.yscale('log')plt.show()# 打印具体数值print("Memory Usage Analysis (MB):")print("Seq Length | Self-Attention | RNN")print("-" * 35)for i, seq_len in enumerate(seq_lengths):print(f"{seq_len:9d} | {attention_memory[i]:13.2f} | {rnn_memory[i]:3.2f}")analyze_memory_usage()

5.4 优化技巧

对于实际应用，我们可以采用以下优化技巧：

1. 梯度检查点：用时间换空间，减少内存使用
2. 稀疏注意力：只计算重要位置的注意力
3. Flash Attention：优化内存访问模式
4. 混合精度：使用FP16减少内存和计算量

class OptimizedSelfAttention(nn.Module):def __init__(self, d_model, num_heads, max_seq_len=1024):super().__init__()self.d_model = d_modelself.num_heads = num_headsself.d_k = d_model // num_heads# 使用fused attention（如果可用）self.use_flash_attention = hasattr(F, 'scaled_dot_product_attention')if not self.use_flash_attention:self.W_q = nn.Linear(d_model, d_model, bias=False)self.W_k = nn.Linear(d_model, d_model, bias=False)self.W_v = nn.Linear(d_model, d_model, bias=False)else:self.qkv = nn.Linear(d_model, 3 * d_model, bias=False)self.W_o = nn.Linear(d_model, d_model)def forward(self, x, mask=None):if self.use_flash_attention:return self._flash_attention_forward(x, mask)else:return self._standard_attention_forward(x, mask)def _flash_attention_forward(self, x, mask=None):"""使用PyTorch 2.0的Flash Attention"""batch_size, seq_len, d_model = x.size()# 计算QKVqkv = self.qkv(x)q, k, v = qkv.chunk(3, dim=-1)# 重塑为多头形式q = q.view(batch_size, seq_len, self.num_heads, self.d_k).transpose(1, 2)k = k.view(batch_size, seq_len, self.num_heads, self.d_k).transpose(1, 2)v = v.view(batch_size, seq_len, self.num_heads, self.d_k).transpose(1, 2)# 使用Flash Attentionoutput = F.scaled_dot_product_attention(q, k, v, attn_mask=mask,dropout_p=0.0 if not self.training else 0.1,is_causal=False)# 重塑输出output = output.transpose(1, 2).contiguous().view(batch_size, seq_len, d_model)output = self.W_o(output)return output, None  # Flash Attention不返回权重

第六章：总结与展望

6.1 关键要点回顾

通过这篇文章，我们深入探讨了Self-Attention机制的方方面面：

数学原理层面：

• 从内积相似度到softmax归一化，每一步都有其深刻的数学含义
• 缩放因子$\sqrt{d_k}$的作用是防止softmax进入饱和区
• 注意力权重的归一化保证了概率分布的性质

实现细节层面：

• 从NumPy的基础实现到PyTorch的优化版本
• 多头注意力通过并行计算多个注意力子空间
• 掌握了完整的前向传播和反向传播流程

性能特点层面：

• Self-Attention的$O(n^2)$复杂度vs RNN的$O(n)$复杂度权衡
• 并行计算能力是Self-Attention的最大优势
• 直接的长距离依赖建模能力解决了RNN的痛点

应用实例层面：

• 文本分类、机器翻译等任务中的具体应用
• 注意力可视化帮助我们理解模型的内部机制
• Cross-Attention在编码器-解码器架构中的重要作用

6.2 注意力机制的核心价值

Self-Attention之所以如此重要，不仅因为它的技术优势，更因为它代表了一种新的建模思路：

1. 动态权重分配：不同于传统的固定权重，注意力机制根据输入动态调整
2. 全局信息整合：每个位置都能直接访问所有其他位置的信息
3. 可解释性：注意力权重提供了模型决策过程的直观解释
4. 可扩展性：从单头到多头，从自注意力到交叉注意力，具有良好的扩展性

6.3 注意力机制的局限性与挑战

尽管Self-Attention很强大，但它也面临一些挑战：

计算复杂度挑战：

• $O(n^2)$的复杂度对长序列处理造成困难
• 内存使用随序列长度平方增长

归纳偏置不足：

• 缺乏天然的位置信息，需要额外的位置编码
• 需要大量数据才能学到有效的模式

解释性争议：

• 注意力权重不一定反映真实的"注意力"
• 可能存在误导性的解释

6.4 未来发展方向

Self-Attention机制仍在不断发展，主要方向包括：

效率优化方向：

• 线性注意力：Linformer、Performer等线性复杂度方法
• 稀疏注意力：局部注意力、滑动窗口注意力
• Flash Attention：内存高效的注意力计算

架构创新方向：

• 混合架构：结合CNN、RNN的优势
• 层次化注意力：多尺度的注意力机制
• 自适应注意力：根据任务动态调整注意力模式

理论深化方向：

• 数学理论：更深入的理论分析和收敛性证明
• 认知科学：与人类注意力机制的对比研究
• 信息论：从信息论角度理解注意力的本质

6.5 实践建议

对于想要在实际项目中应用Self-Attention的开发者，我们提供以下建议：

选择合适的实现：

• 短序列（<512）：标准Self-Attention即可
• 中等序列（512-2048）：考虑优化实现如Flash Attention
• 长序列（>2048）：必须使用稀疏注意力或线性注意力

调优要点：

• 注意力头数通常设为8-16
• 学习率需要仔细调整，通常比CNN/RNN更小
• Dropout和权重衰减对防止过拟合很重要

监控指标：

• 注意力熵：观察注意力的集中程度
• 梯度范数：监控训练稳定性
• 内存使用：确保不会出现OOM

6.6 下一步学习路径

掌握了Self-Attention基础后，建议按以下路径继续学习：

1. 多头注意力机制：理解为什么需要多个注意力头
2. Transformer完整架构：学习编码器-解码器结构
3. 位置编码技术：绝对位置编码vs相对位置编码
4. 预训练技术：BERT、GPT等预训练模型的原理
5. 高级优化技术：混合精度、梯度累积等训练技巧

结语

Self-Attention机制是现代深度学习的一个里程碑，它不仅改变了我们处理序列数据的方式，更重要的是，它为我们提供了一种新的思考问题的方式：如何让机器学会"关注"重要的信息。

正如我们在文章开头提到的咖啡厅例子，人类的注意力机制帮助我们在嘈杂的环境中专注于重要的信息。而Self-Attention机制，正是我们赋予机器这种能力的第一步。

通过深入理解Self-Attention的数学原理、实现细节和应用实例，我们不仅掌握了一个强大的技术工具，更重要的是，我们理解了它背后的思考方式。这种思考方式，将帮助我们在人工智能的道路上走得更远。

在下一篇文章《多头注意力深度剖析：为什么需要多个头》中，我们将继续探讨多头注意力机制，看看如何通过多个"注意力头"来捕获更丰富的信息模式。敬请期待！

---

参考资料

1. Vaswani, A., et al. (2017). Attention is all you need. In Advances in neural information processing systems.
2. Devlin, J., et al. (2018). BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding.
3. Radford, A., et al. (2019). Language models are unsupervised multitask learners.

延伸阅读

• The Illustrated Transformer
• The Annotated Transformer
• Attention Mechanisms in Computer Vision