目录
返回数组最后一个元素
2787.将一个数字表示成幂的和的方案数
326.3的幂
1780.判断一个数字是否可以表示成三的幂的和
342.4的幂
返回数组最后一个元素
1.请你编写一段代码实现一个数组方法,使任何数组都可以调用 array.last() 方法,这个方法将返回数组最后一个元素。如果数组中没有元素,则返回 -1 。
你可以假设数组是 JSON.parse 的输出结果。
示例 1 :
输入:nums = [null, {}, 3]
输出:3
解释:调用 nums.last() 后返回最后一个元素: 3。
示例 2 :
输入:nums = [] 输出:-1 解释:因为此数组没有元素,所以应该返回 -1。
提示:
arr是一个有效的 JSON 数组0 <= arr.length <= 1000
Array.prototype.last = function() {return this.length ? this.at(-1) : -1
};// at支持负索引,-1表示倒数第一个位置,-2则是倒数第二,以此类推Array.prototype.last = function() {return this.length ? this.[this.length-1] : -1
};2787.将一个数字表示成幂的和的方案数
2787. 将一个数字表示成幂的和的方案数
提示
给你两个 正 整数 n 和 x 。
请你返回将 n 表示成一些 互不相同 正整数的 x 次幂之和的方案数。换句话说,你需要返回互不相同整数 [n1, n2, ..., nk] 的集合数目,满足 n = n1x + n2x + ... + nkx 。
由于答案可能非常大,请你将它对 109 + 7 取余后返回。
比方说,n = 160 且 x = 3 ,一个表示 n 的方法是 n = 23 + 33 + 53 。
示例 1:
输入:n = 10, x = 2 输出:1 解释:我们可以将 n 表示为:n = 32 + 12 = 10 。 这是唯一将 10 表达成不同整数 2 次方之和的方案。
示例 2:
输入:n = 4, x = 1 输出:2 解释:我们可以将 n 按以下方案表示: - n = 41 = 4 。 - n = 31 + 11 = 4 。
提示:
1 <= n <= 3001 <= x <= 5
var numberOfWays = function (n, x) {const MOD = Math.pow(10,9)+7const current = []// 获取以x为幂的数组,大小不超过nfor(let i=1;i<=n;i++){current[i]=Math.pow(i,x)}// 创建一个长度为n+1,初始为0的数组const dp = new Array(n+1).fill(0)dp[0]=1// 核心代码for(num of current){for(let k=n;k>=num;k--){dp[k]=(dp[k-num]+dp[k])%MOD}}return dp[n]
};理解:这是一个01背包问题,我们先回顾一下01背包问题的初始形态是什么样子的,即有一个最大承重为 W 的背包,有价格为v,重量为w的商品一堆,需要在不超过最大承重的前提下完成所选商品最贵的问题。我们可以用二维数组和一维数组来解决这个问题,关键在于,我放了和不放哪个会比较大?
二维数组:
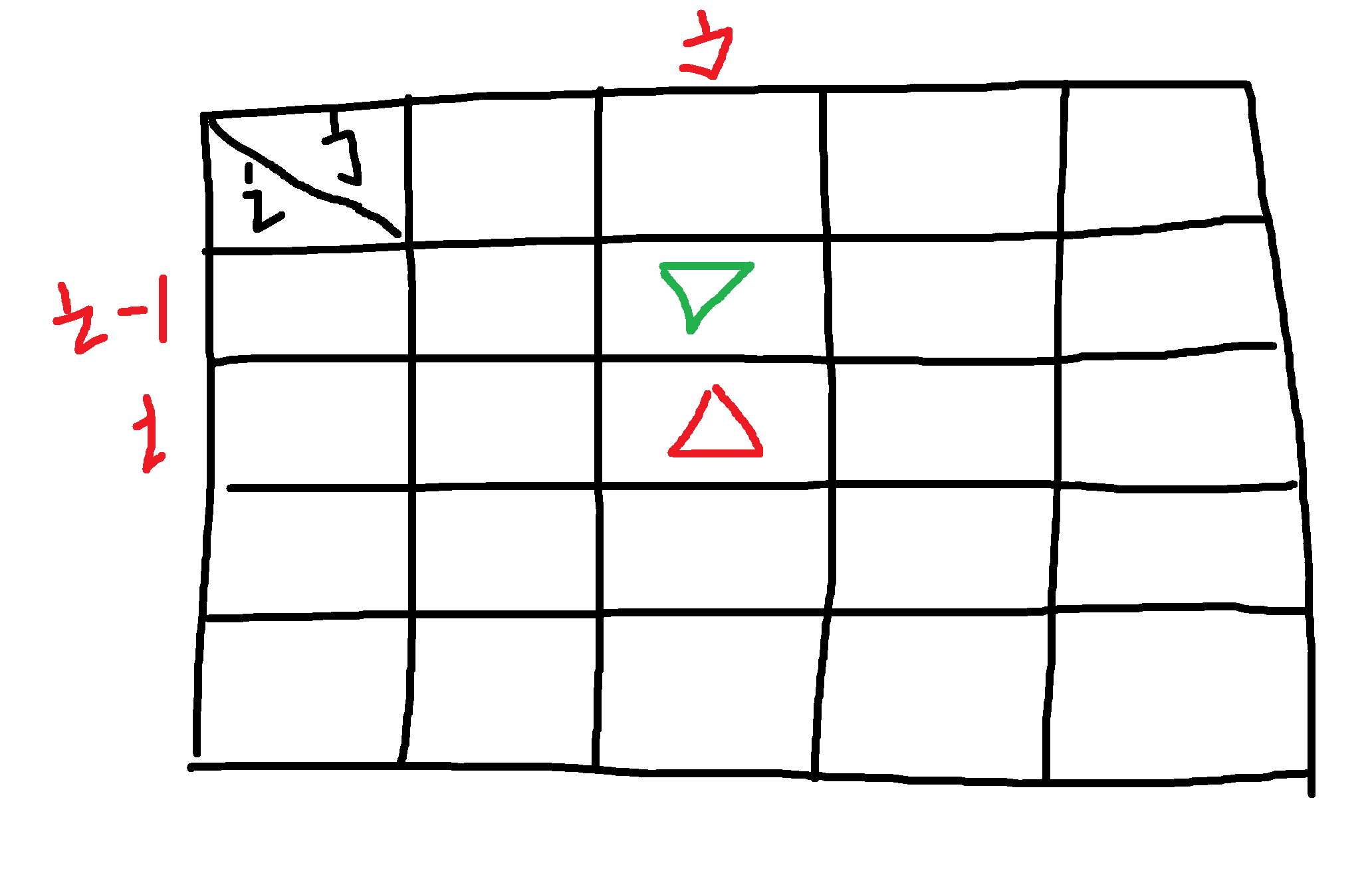
此时我的背包中的物品装到了dp[i][j]的红色三角形位置,此时我有俩个选项,
一是、我不把v[i]和w[i]的商品放进去,也就是dp[i-1][j]的绿色三角形位置,这么理解这个绿色三角形的位置吧,i-1 是上一个价格的所有状态,dp[i-1][j] 可以被理解成再上一个价格在 j 重量时候的状态;
二是、然后就是我放商品进去dp[i-1][j-w[i]]+v[i] ,可以这么理解dp[i-1][j-w[i]],把上一次状态调到刚好可以放下这个新商品的体积,这个时候的重量应该是 目前状态的重量-新商品的体积对吧,也就是j-w[i],然后在这个状态上加上新商品的价格。
for(let i=1;i<=V;i++){for(let j=1;j<=W;j++){if(j>w[i]){dp[i][j] = Max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])}}
}一维数组:
其实由二维数组可以发现一个点,就是你的重量必须是要按顺序从小增到大的,也就是 j 既是索引,又代表了实际重量,那么一维数组中索引代表重量不就行了吗,然后具体数值是价格
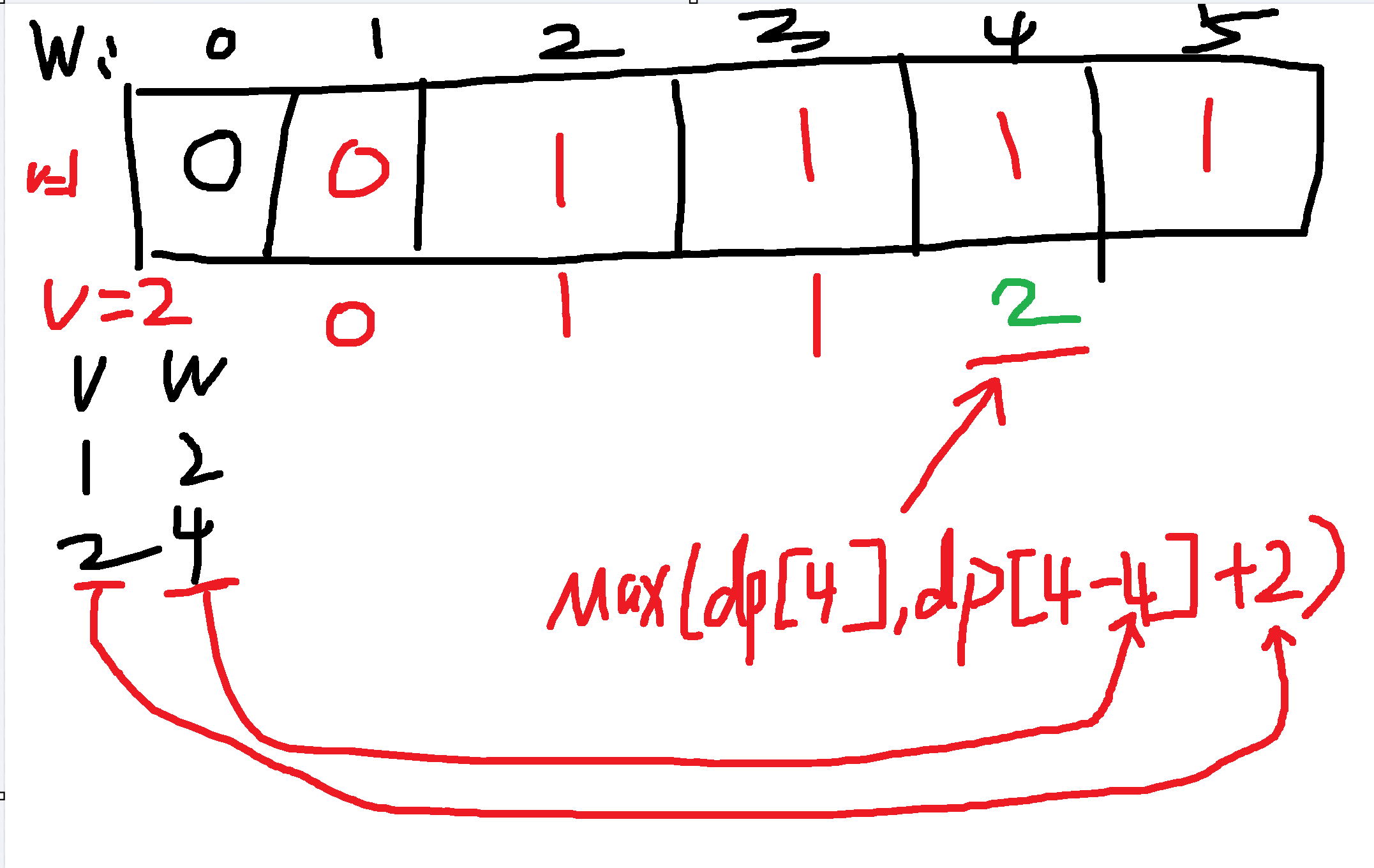
注意我下面写的max(dp[i],dp[i-w[i]]+v[i]) 这个是基于v=1的时候的dp
OK,现在我们类比到这一题上面来

这里的n是不是就相当于是最大重量,由x次幂组成的数组[num1,num2,num3...],不就代表了索引和实际值相同的重量吗
举个例子 n=10 x=2
| 0 | 1 | 2 | 4 | 9 | |
| 0 | 1 | ||||
| 1 | |||||
| 2 | |||||
| 3 | dp[3]+dp[3-1] | ||||
| ... | dp[...]+dp[...-1] | ||||
| 10 | dp[10]+dp[10-1] | dp[10]+dp[10-2] |
上面的表格出来是不是就能看懂了,两层循环,先遍历n,然后里面嵌套是实现放不放num数组里的值,而且为什么这里不是用max比较大小呢?是因为无论我放不放都是一种方案,只要结果是实现了和等于n,所以应该是放和不放的情况加起来,用大白话理解就是,我有一系列的商品,我只是为了凑单,不管我放不放这一件它都是一种方案。
326.3的幂
326. 3 的幂
给定一个整数,写一个函数来判断它是否是 3 的幂次方。如果是,返回 true ;否则,返回 false 。
整数 n 是 3 的幂次方需满足:存在整数 x 使得 n ==
示例 1:
输入:n = 27 输出:true
示例 2:
输入:n = 0 输出:false
示例 3:
输入:n = 9 输出:true
示例 4:
输入:n = 45 输出:false
提示:
-<= n <=
- 1
进阶:你能不使用循环或者递归来完成本题吗?
// 循环
var isPowerOfThree = function(n) {let flag = nwhile(flag>=1){if(flag===1){return true;break}flag=flag/3 }return false
};// 不循环
var isPowerOfThree = function(n) {return n>0 && Math.pow(3,19)%n===0 ?true:false
};题解:循环的做法就是不断除3,一直到等于1就返回true,不等于1就为false;不循环的做法就是取模,设置一个最大的3的幂(n<3的19次幂),然后对n取模,如果取出来为0就说明是3的幂,为什么呢?因为3是质数,大家都知道质数只能被1和自身整除,所以在一个不断取模的过程中不会有其他数字干扰,举个例子:4不是质数吧,如果我们要判断一个数是否为4的幂,再用这个取模方法就不行了,假如用 对2和4分别取模,是不是得出来的结果都是0?但是2不是4的幂对吧,所以取模判断这个方法只能对质数使用。
1780.判断一个数字是否可以表示成三的幂的和
1780. 判断一个数字是否可以表示成三的幂的和
给你一个整数 n ,如果你可以将 n 表示成若干个不同的三的幂之和,请你返回 true ,否则请返回 false 。
对于一个整数 y ,如果存在整数 x 满足 y == 3x ,我们称这个整数 y 是三的幂。

var checkPowersOfThree = function (n) {// n没有除到底就继续循环while(n>1){if(n%3===1){n=(n-1)/3}else if(n%3===0){n=n/3}else{// 除不出来说明不能展开为3的幂的和return false}}return true
};题解:
大家看到这题会不会想到之前写的那个背包问题?用01背包也能做,不过有俩个嵌套循环大大降低了代码效率,而且会超时;
大家可以观察一下,不知道大家的数学老师有没有告诉过大家一个小技巧,如果有一个超大的数,判断是否能被三整除,只需要把这个数的每一位拆分开,然后相加,这个时候数字是不是小了很多,我们就能判断是否能被3整除了,例如:1233219这个数,拆分:1+2+3+3+2+1+9=21 =>2+1=3; 是不是说明1233219可以被3整除;
题目中说了,都是3的幂,且不同,那么我们可以这么做,我每次都除3,是不是剩下来的数不是余1,就是刚好除完?ok,可能有点抽象,我们来举一个例子:
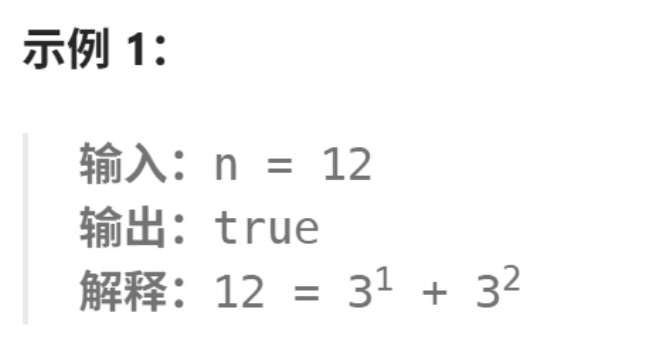
对吧,那么现在我们对这个数除3,也就变成了
是不是余1,然后我们-1继续除3,
,刚好为0,我猜你想知道为什么会这样,题目有前提,每个都是3的幂,且不相同,那么我对一个全是3的幂除3,是不是每个数还是不同,只要我一直除下去,能除的尽,是不是就能说明n是可以被展开为不同的3的幂的和
342.4的幂
342. 4的幂
给定一个整数,写一个函数来判断它是否是 4 的幂次方。如果是,返回 true ;否则,返回 false 。
整数 n 是 4 的幂次方需满足:存在整数 x 使得 n ==

/*** @param {number} n* @return {boolean}*/
var isPowerOfFour = function(n) {while(n>=1){if(n===1){return true}n=n/4}return false
};/*** @param {number} n* @return {boolean}*/
var isPowerOfFour = function(n) {return n>0 && n%3===1 && Math.pow(2,31)%n===0?true:false
};题解:
这题大家是不是很眼熟,前面我们也写了关于判断是否为3的幂,最直接的判断还是直接除啊,一直除到底;
另一种不需要循环的,我们知道,如果一个数是4的幂的话,肯定也是2的幂,所以我们可以缩小范围去做,于是就有了
Math.pow(2,31)%n===0大家都知道二项式定理:
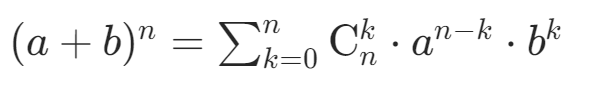
这里可以拆分成: ,
是不是变成了模3
。。。持续更新












跳过登录微软账户,创建本地账户)






