当使用"孩子兄弟表示法"存储树或森林时,最终会呈现出与二叉树类似的形态,
所以树、森林与二叉树之间的转换本质上就是画出采用孩子兄弟表示法存储的树和森林。
一."树->二叉树"的转换:
1.例一:
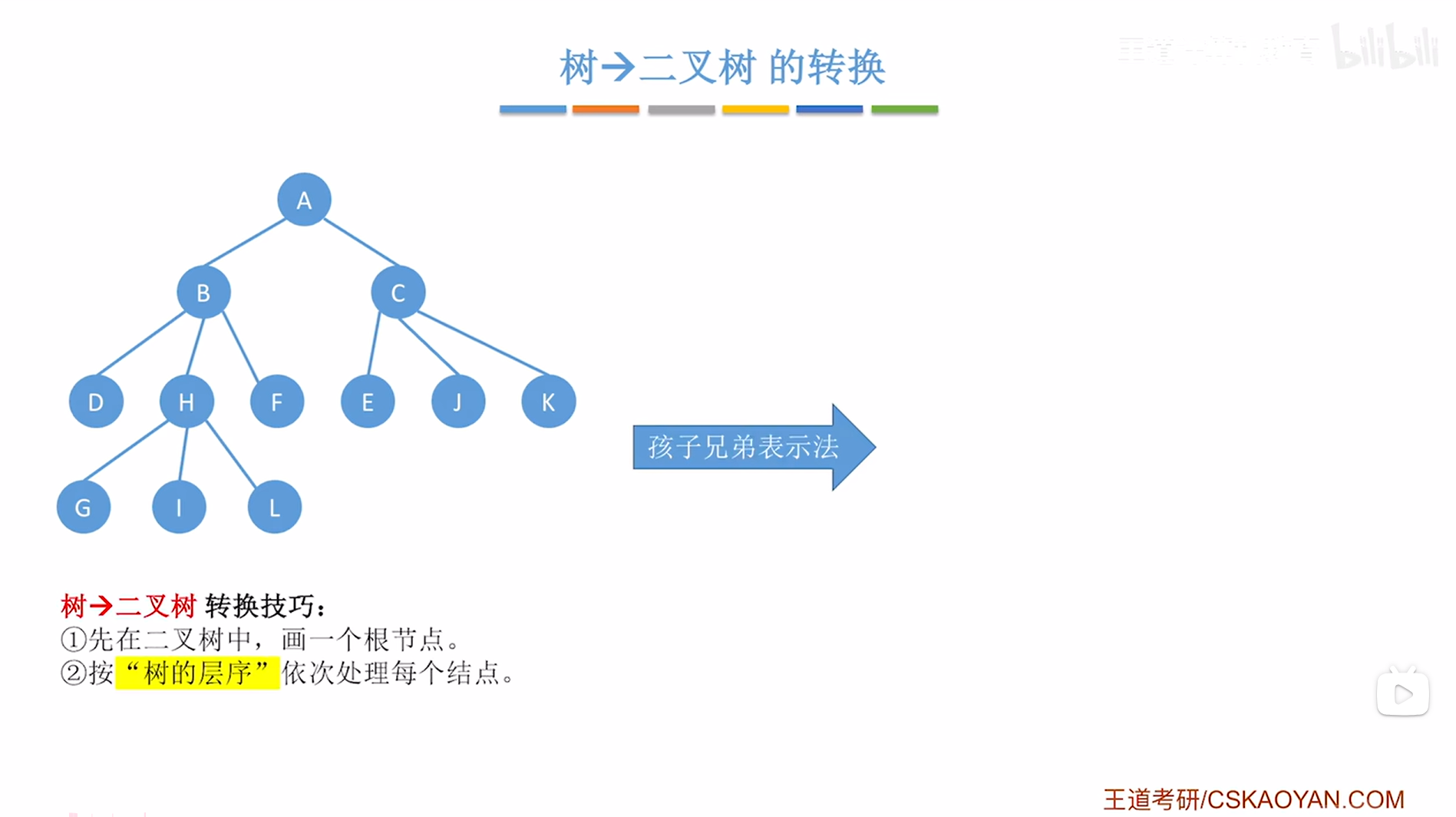
以上述图片左边的树为例,
现将该树转化为二叉树,本质上就是用孩子兄弟表示法存储该树,
"树->二叉树"转换技巧:
- 首先在一棵二叉树中画出树的根节点
- 按"树的层序"依次处理每个结点
上述图片左边的树的根结点为A,因此转换后的二叉树的根结点也为A,
如下图:
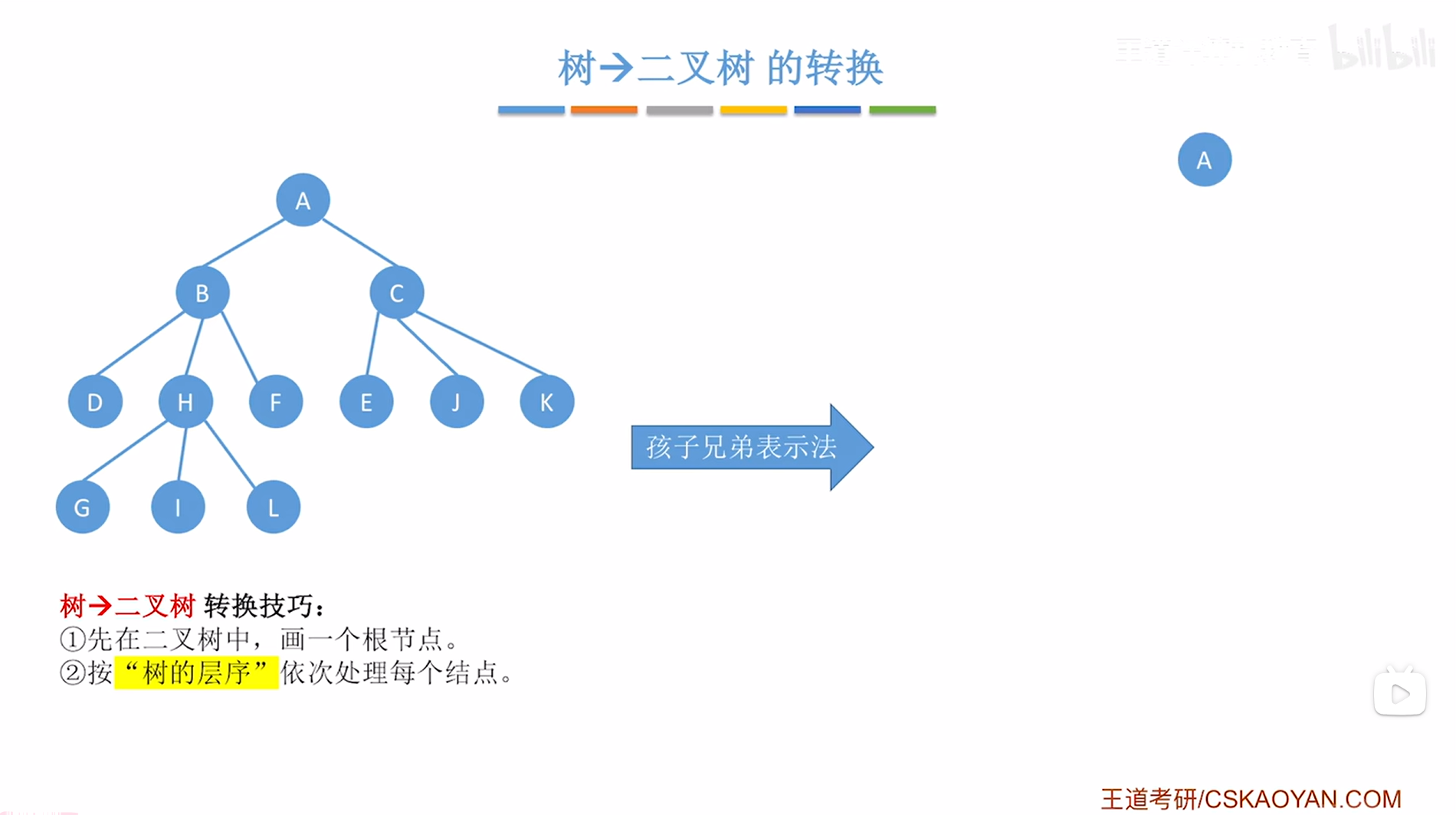
如上图,
接下来需要按"树的层序"依次处理每个结点,这是什么意思呢?
也就是说先处理树中第一层的A,再处理第二层的B、C,接下来处理第三层的D、H、F、E、J、K,最后处理第四层的G、I、L,就是一层一层的按顺序处理结点,按这种方式处理的话不容易乱,
首先处理树中第一层的A,处理的方法如下:
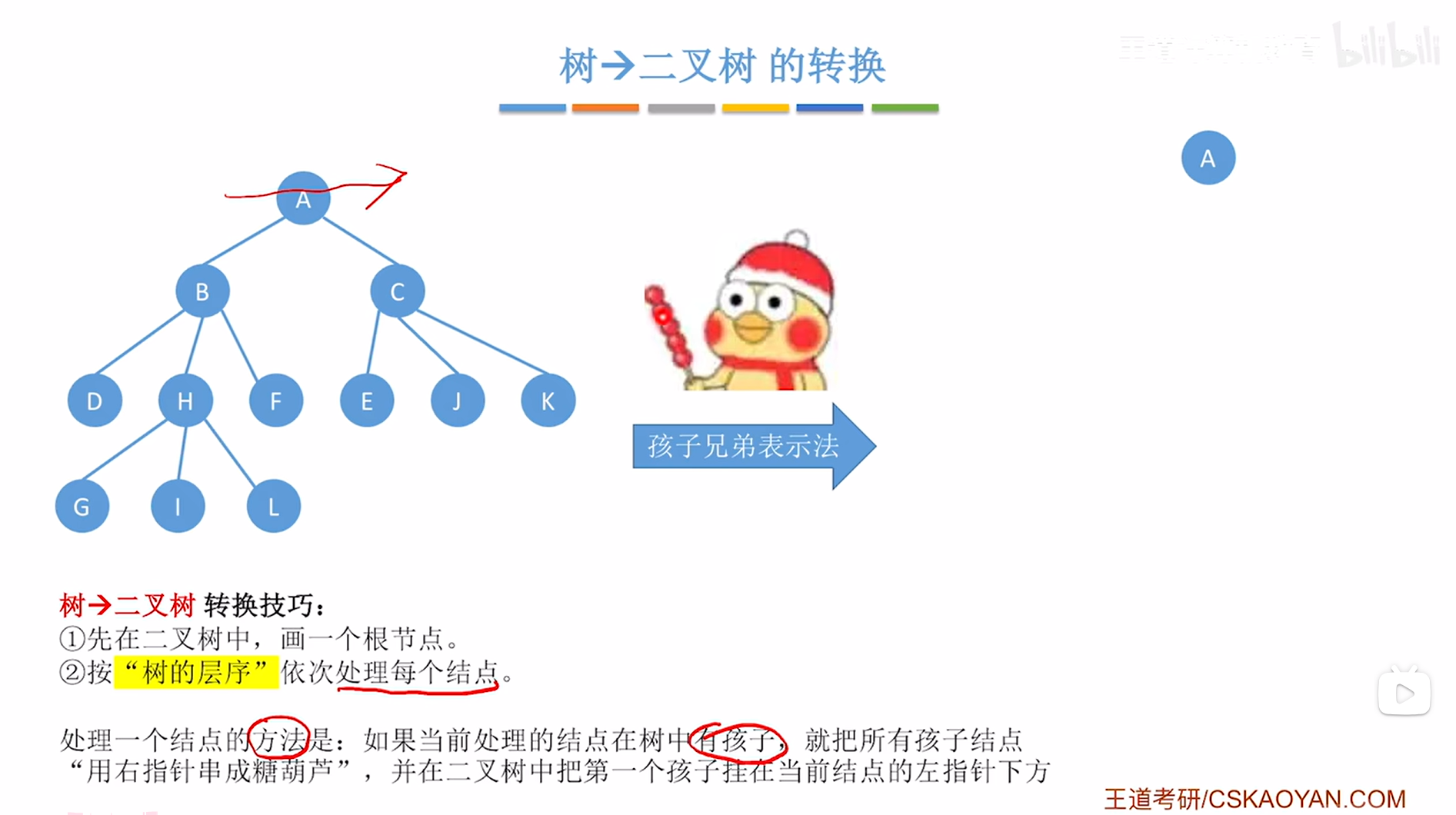
如上图,
首先要观察当前处理的结点即A在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于A结点来说,他有B、C两个孩子,因此需要把B、C用右指针串成一个"冰糖葫芦"的形态,
如下图:
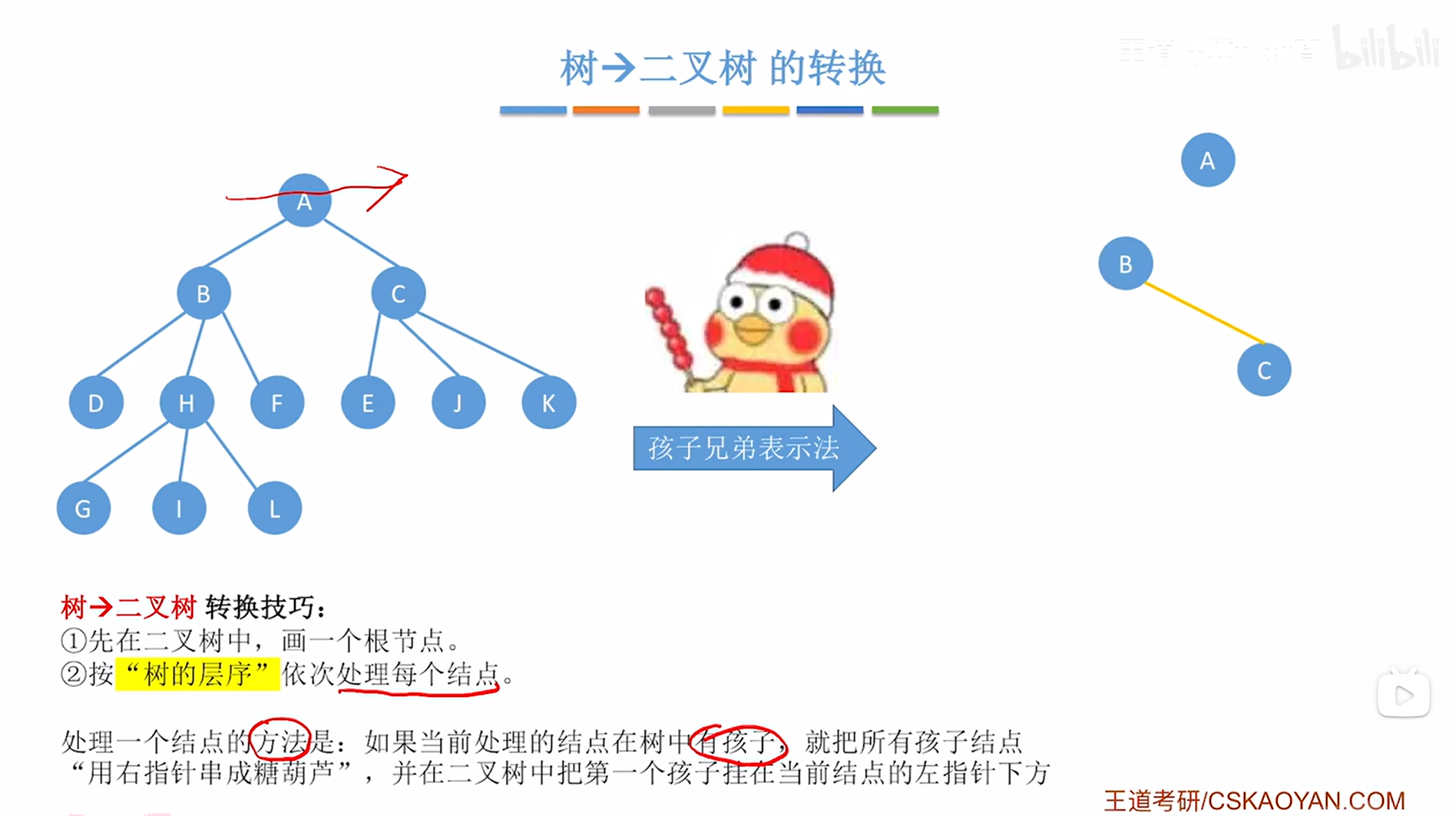
如上图,
接下来要在创建的二叉树中把A结点的第一个孩子即B挂在当前处理的结点即A的左指针上,
如下图:
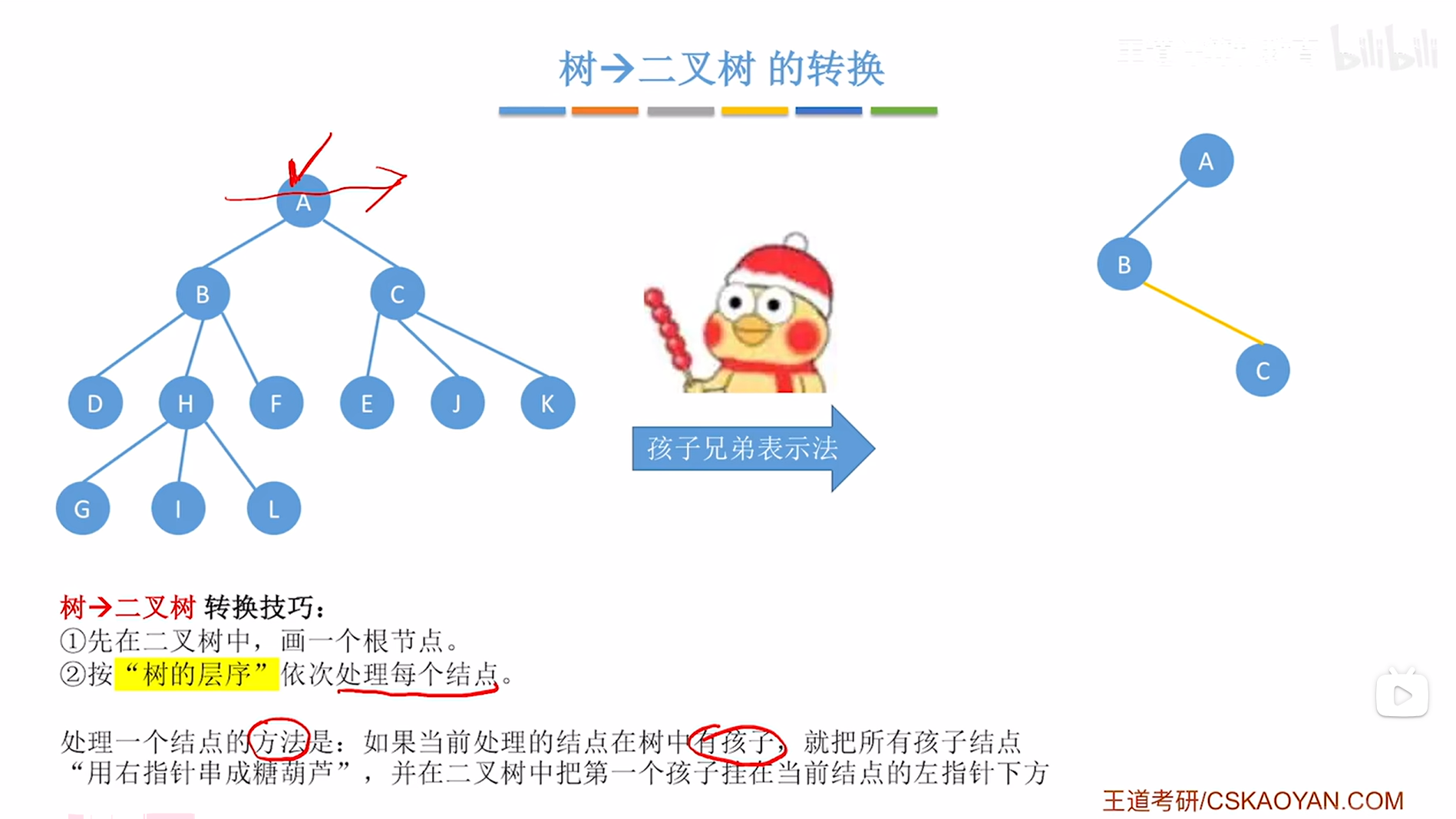
如上图,
A结点处理完毕,接下来处理B结点,同理,
首先要观察当前处理的结点即B在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于B结点来说,他有D、H、F三个孩子,因此需要把D、H、F用右指针串成一个"冰糖葫芦"的形态,
如下图:
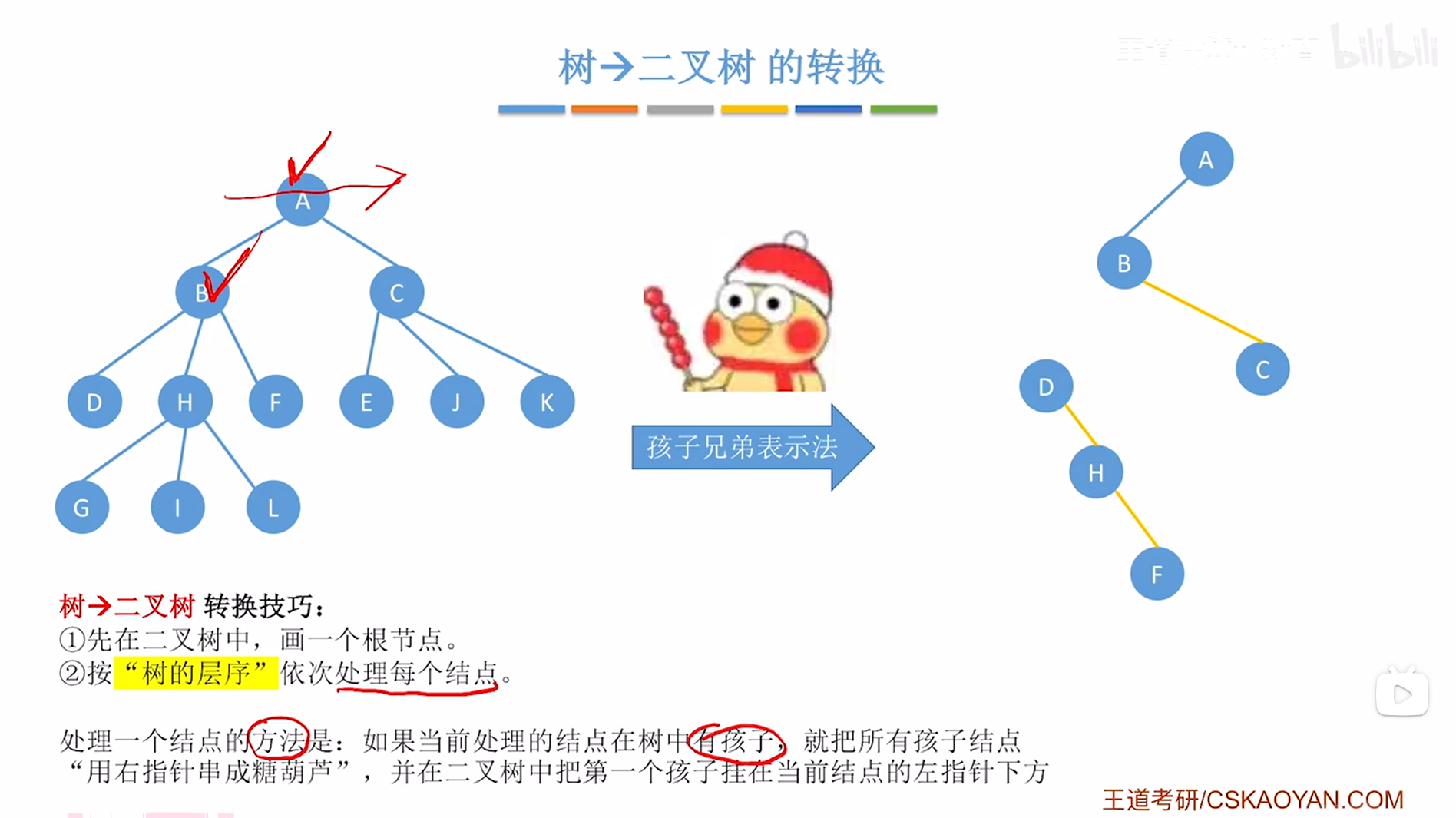
如上图,
接下来要在创建的二叉树中把B结点的第一个孩子即D挂在当前处理的结点即B的左指针上,
如下图:
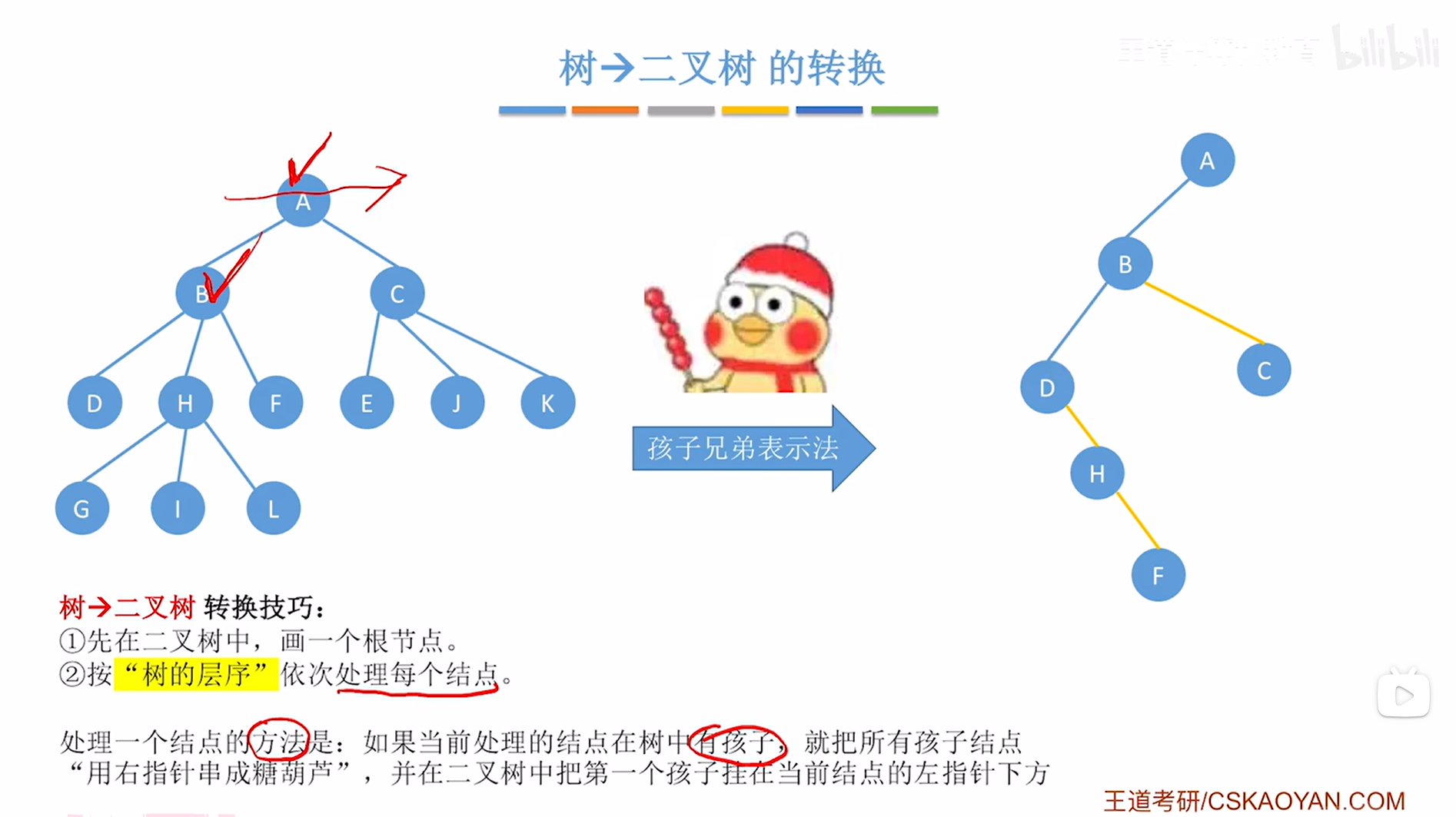
如上图,
B结点处理完毕,接下来处理C结点,同理,
首先要观察当前处理的结点即C在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于C结点来说,他有E、J、K三个孩子,因此需要把E、J、K用右指针串成一个"冰糖葫芦"的形态,
如下图:
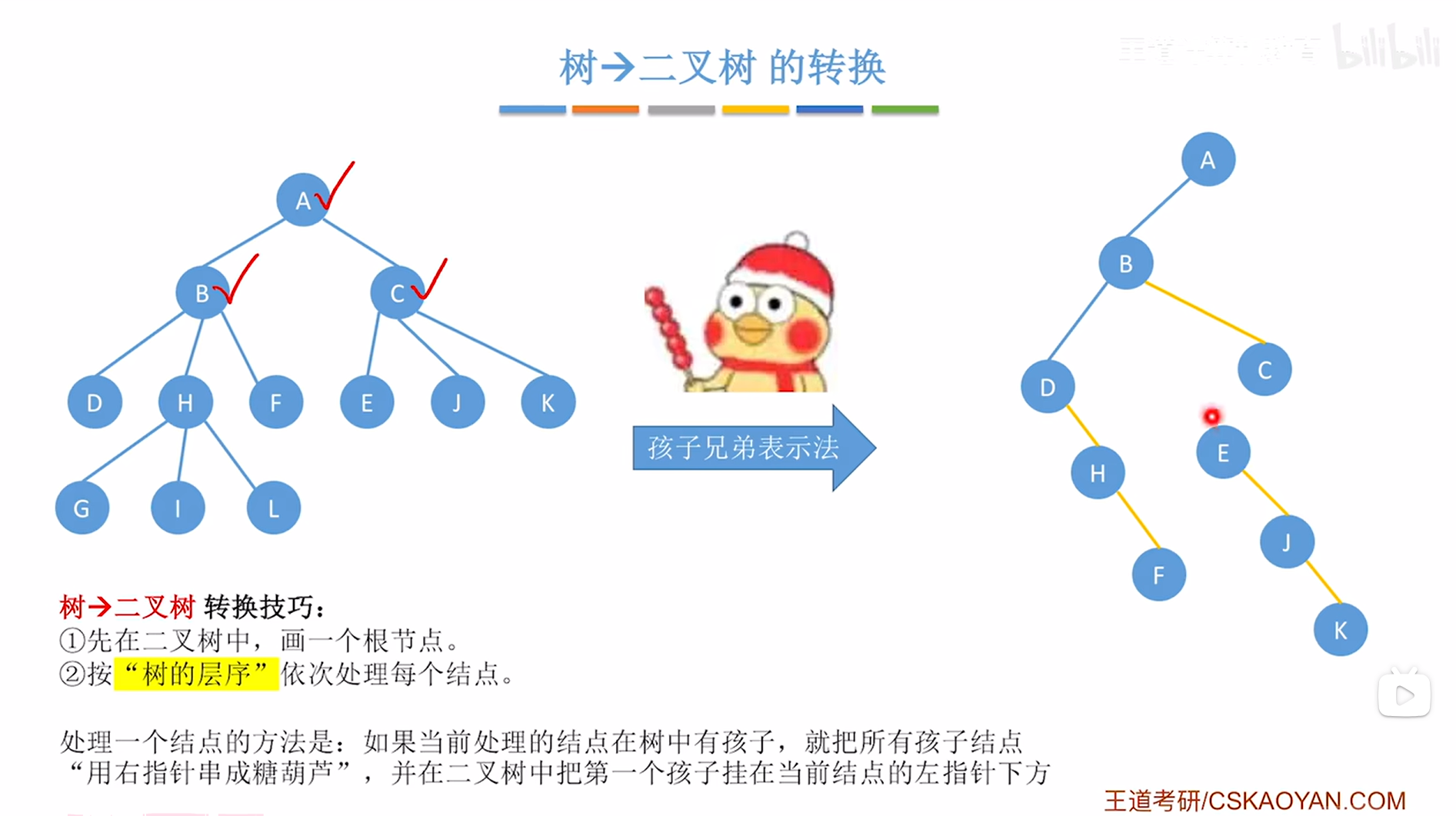
如上图,
接下来要在创建的二叉树中把C结点的第一个孩子即E挂在当前处理的结点即C的左指针上,
如下图:
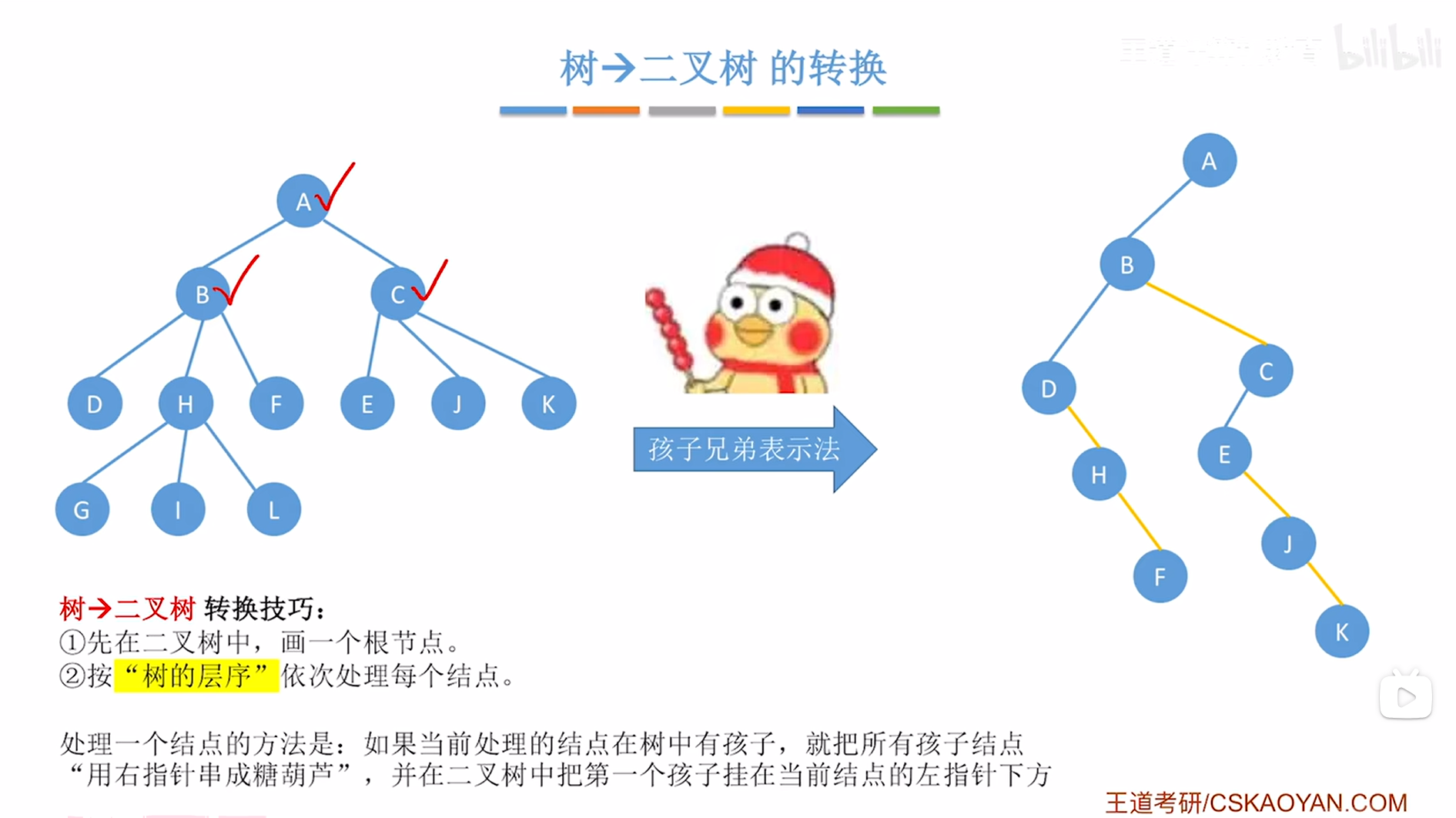
如上图,
C结点处理完毕,接下来按照"树的层序"应该处理D结点,同理,
首先要观察当前处理的结点即D在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于D结点来说,显然没有孩子,所以D结点不需要做任何处理;
D结点处理完毕,接下来处理H结点,同理,
首先要观察当前处理的结点即H在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于H结点来说,他有G、I、L三个孩子,因此需要把G、I、L用右指针串成一个"冰糖葫芦"的形态,
如下图:
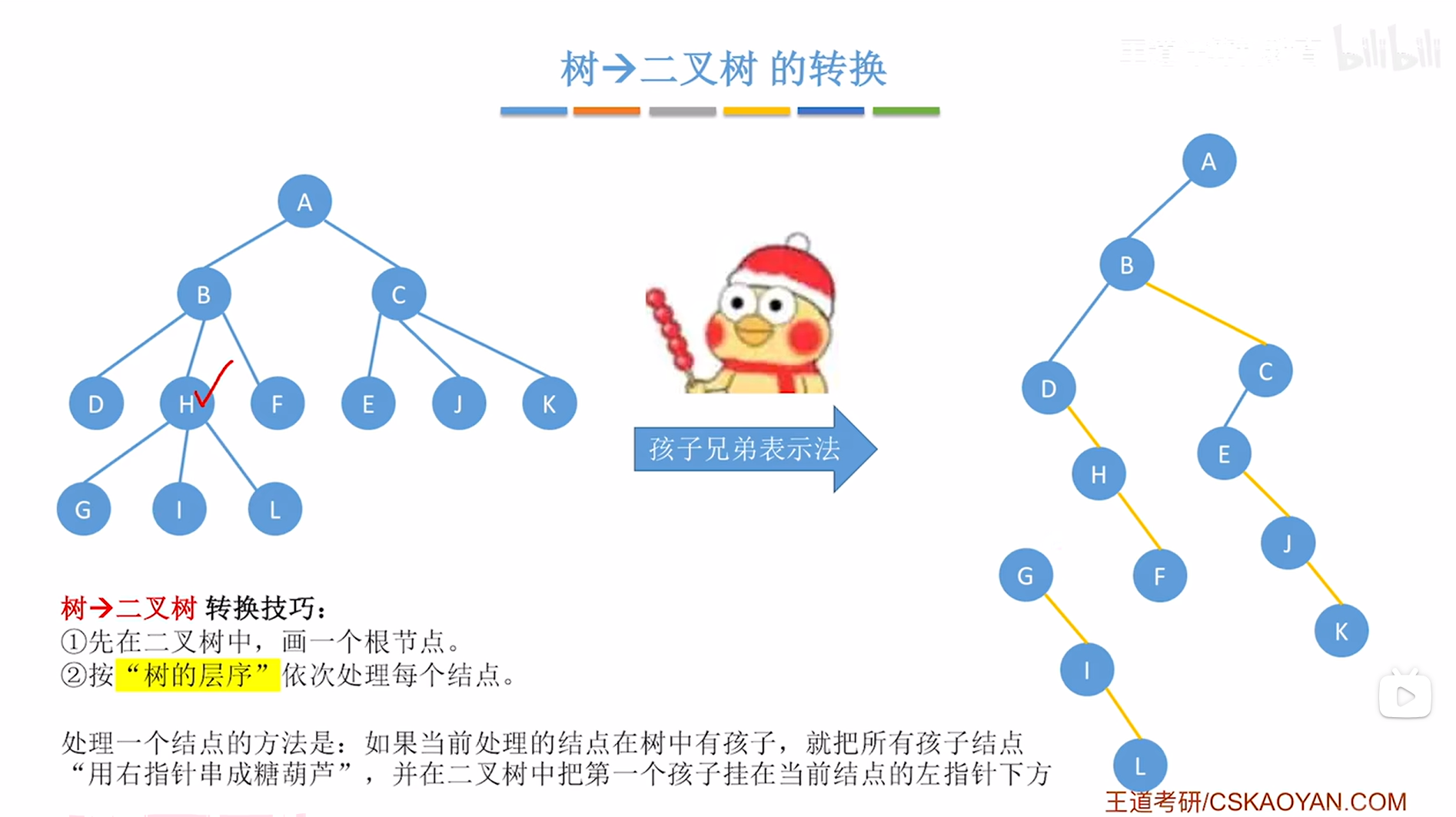
如上图,
接下来要在创建的二叉树中把H结点的第一个孩子即G挂在当前处理的结点即H的左指针上,
如下图:
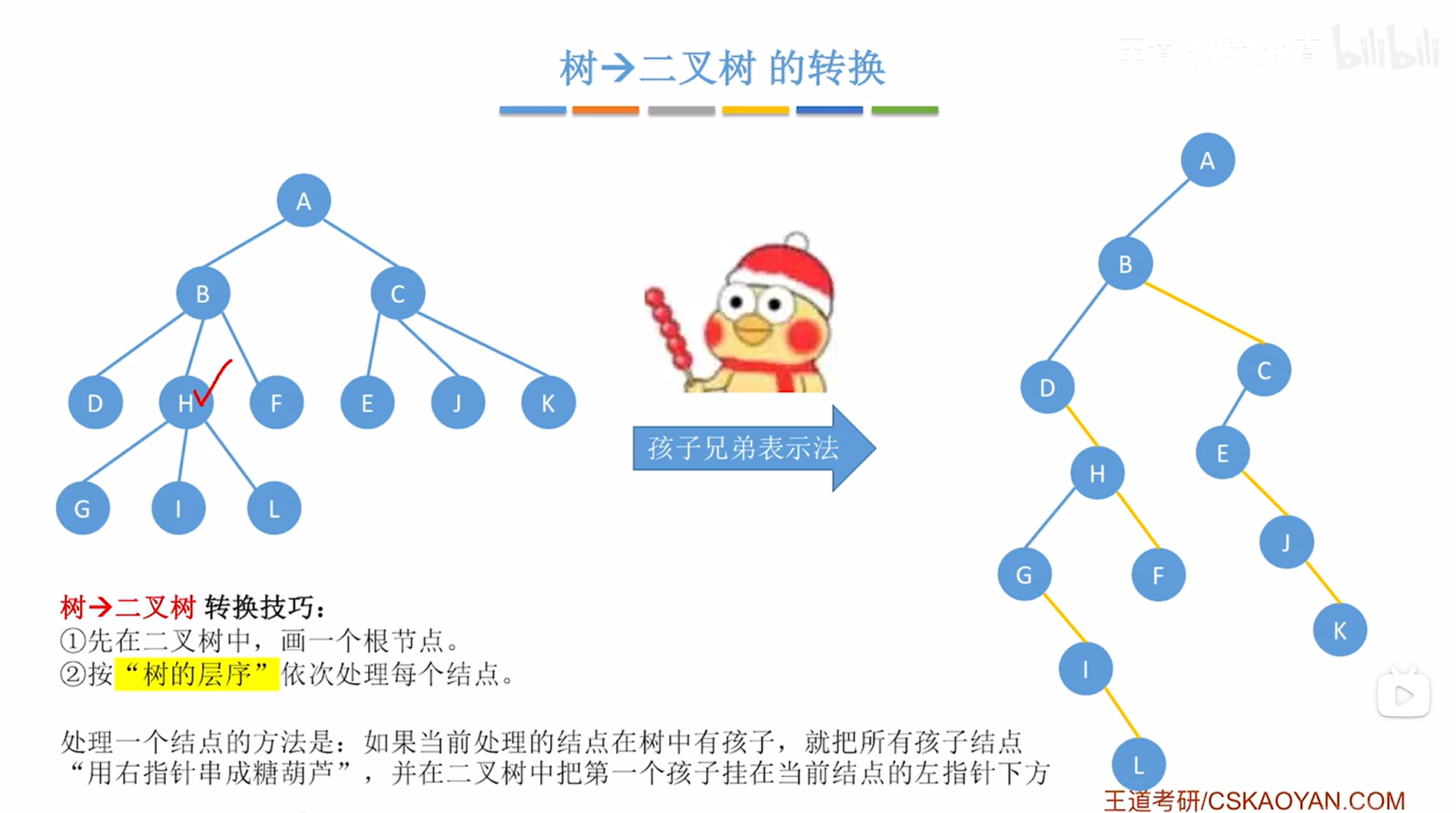
如上图,
H结点处理完毕,接下来按照"树的层序"应该依次处理F、E、J、K、G、I、L结点,同理,
首先要观察当前处理的结点在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于F、E、J、K、G、I、L结点来说,显然都没有孩子,所以F、E、J、K、G、I、L结点都不需要做任何处理,
至此,就完成了"树->二叉树"的转换,
如下图:
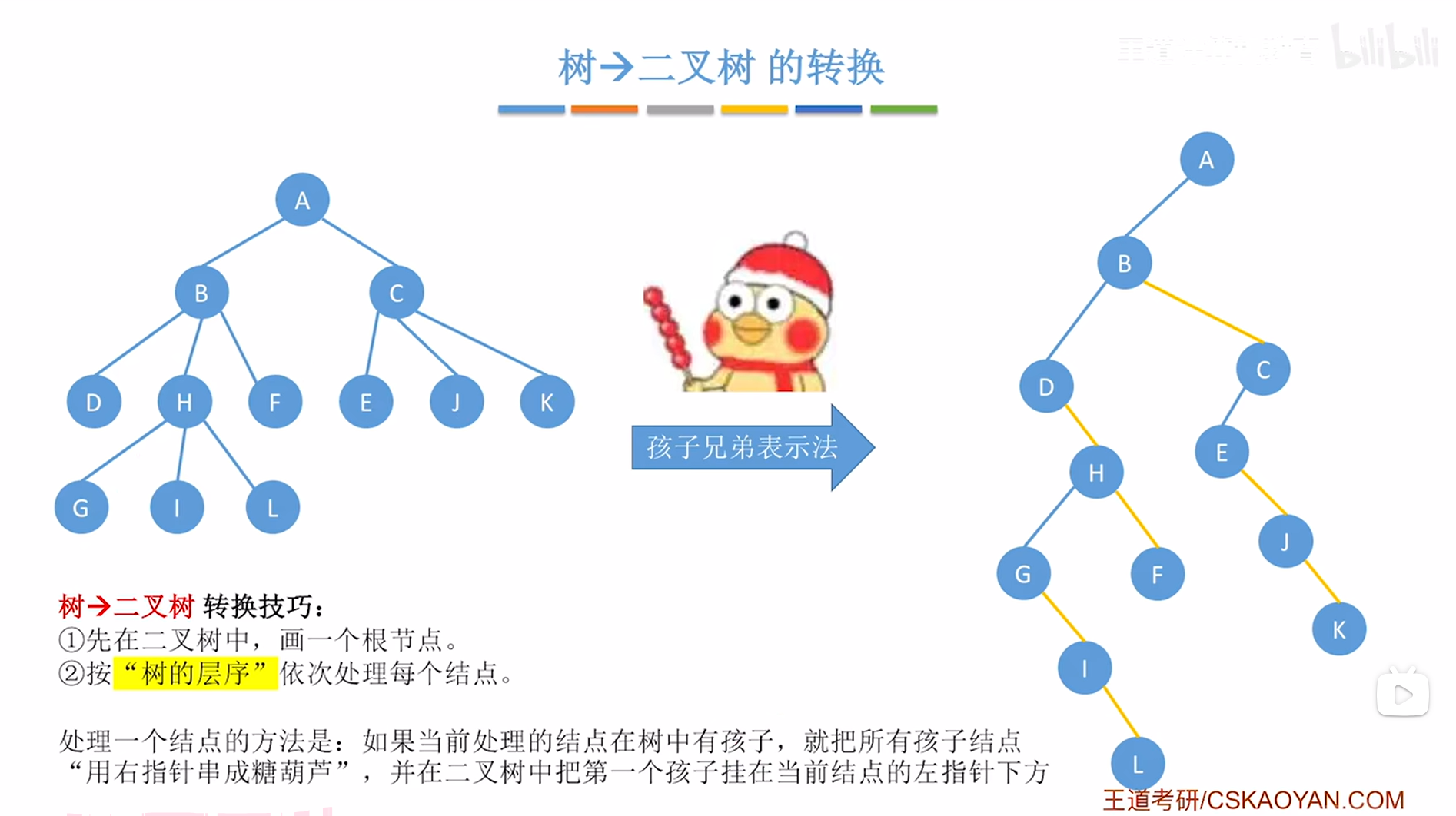
2.例二:原理同例一
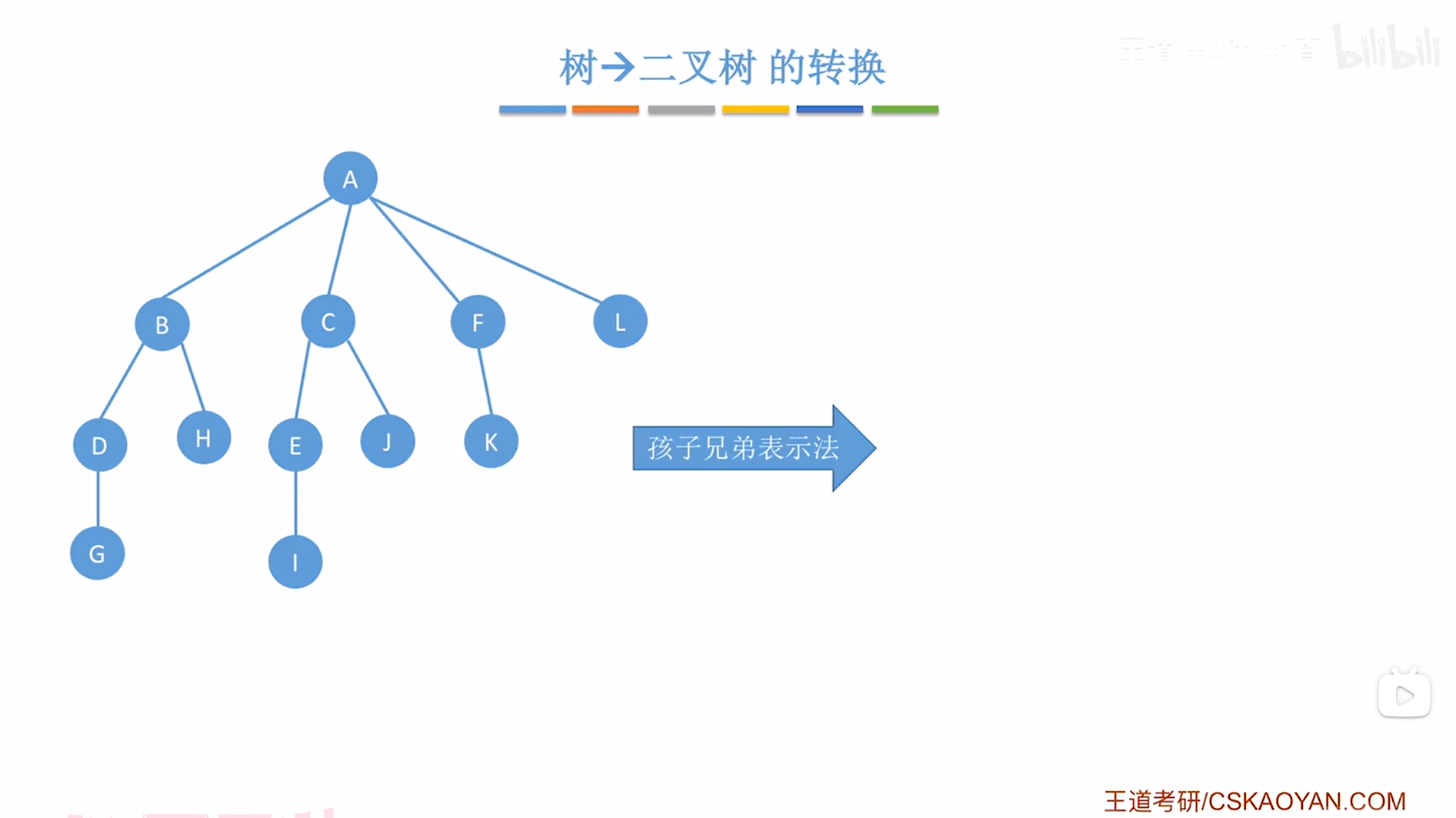
以上述图片左边的树为例,
现将该树转化为二叉树,本质上就是用孩子兄弟表示法存储该树,
上述图片左边的树的根结点为A,因此转换后的二叉树的根结点也为A,
如下图:
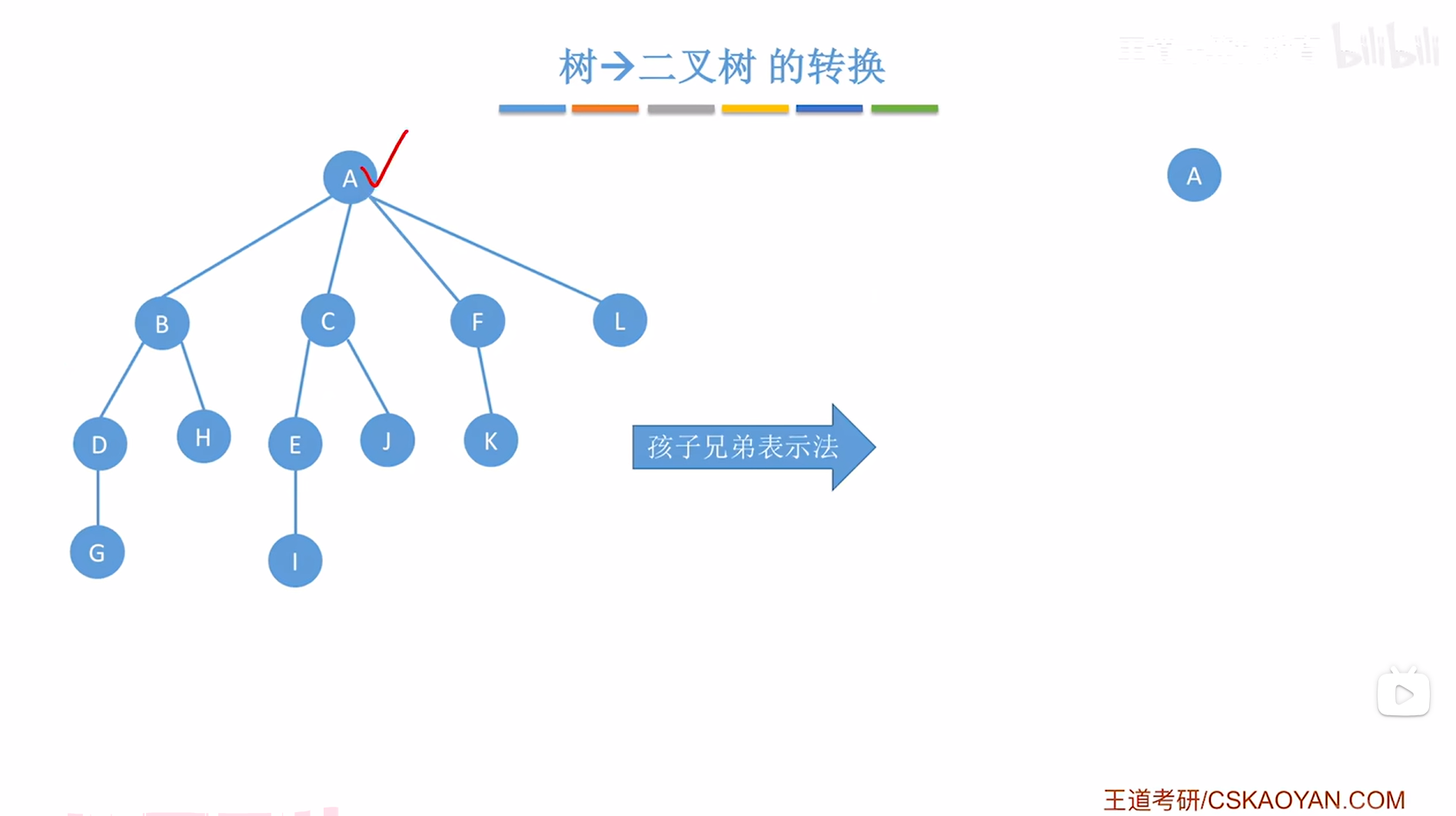
如上图,
首先要观察当前处理的结点即A在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于A结点来说,他有B、C、F、L四个孩子,因此需要把B、C、F、L用右指针串成一个"冰糖葫芦"的形态,
如下图:
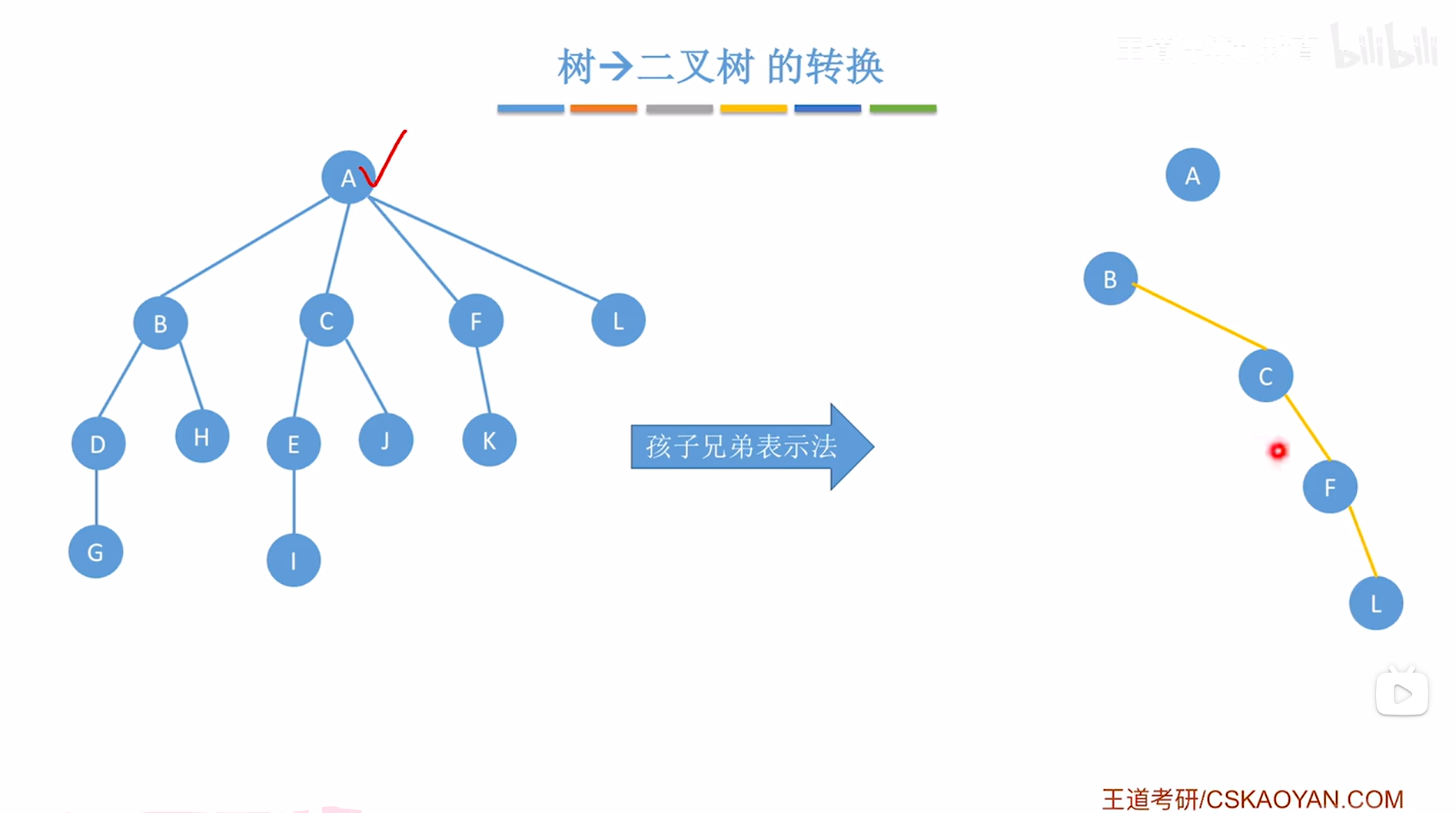
如上图,
接下来要在创建的二叉树中把A结点的第一个孩子即B挂在当前处理的结点即A的左指针上,
如下图:
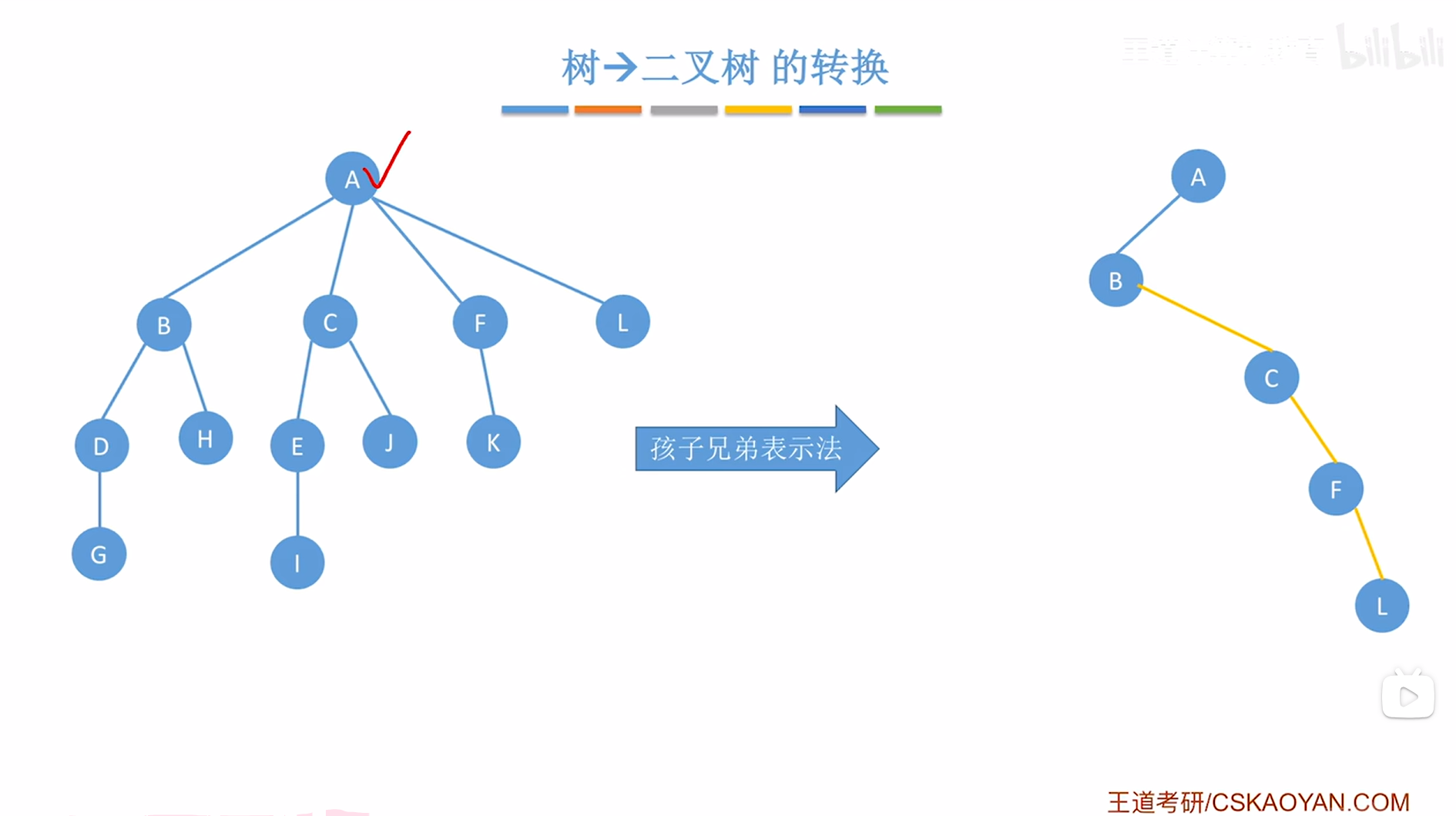
如上图,
A结点处理完毕,接下来需要按"树的层序"依次处理每个结点,因此接下来处理B结点,
首先要观察当前处理的结点即B在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于B结点来说,他有D、H两个孩子,因此需要把D、H用右指针串成一个"冰糖葫芦"的形态,
如下图:
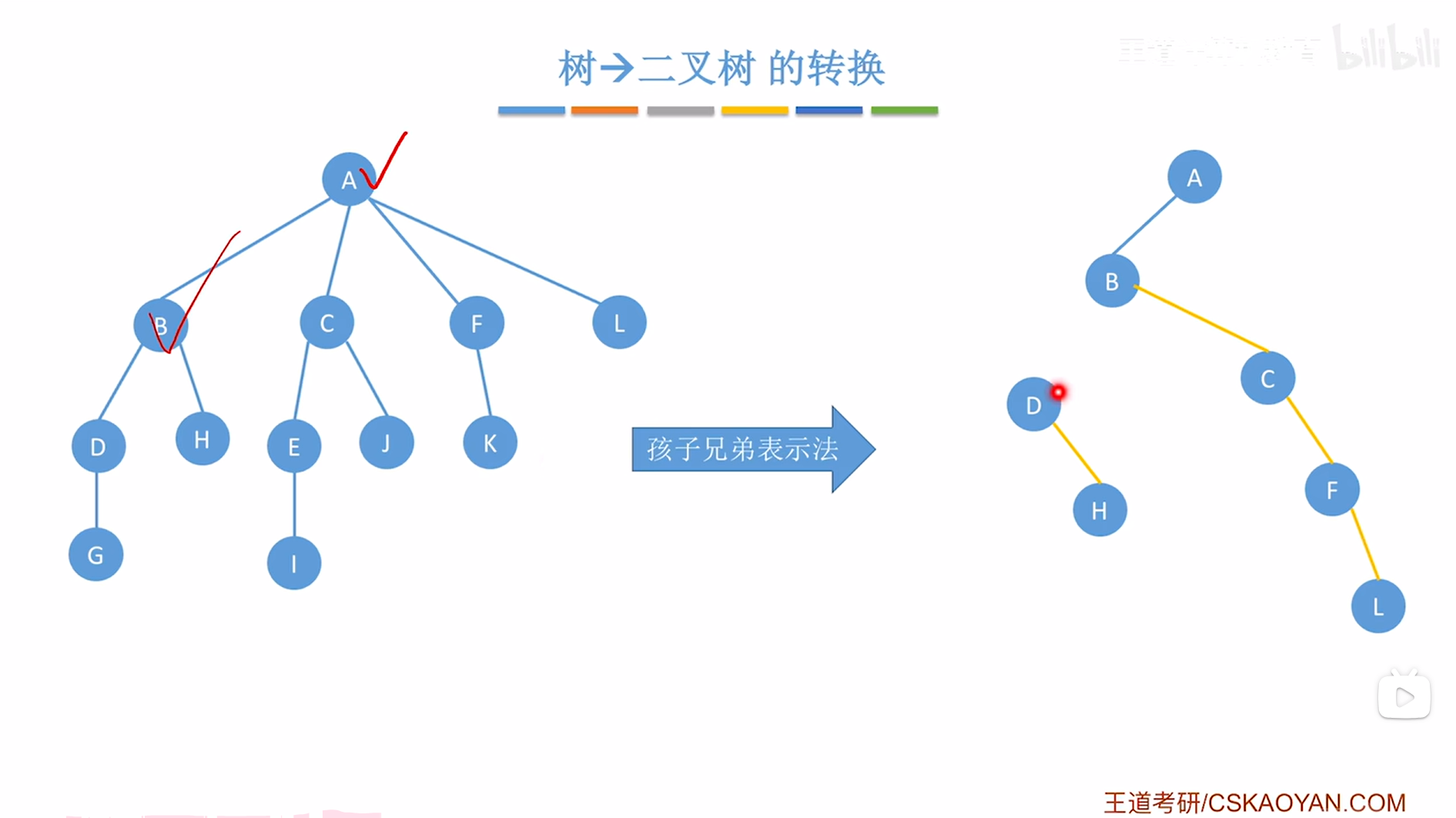
如上图,
接下来要在创建的二叉树中把B结点的第一个孩子即D挂在当前处理的结点即B的左指针上,
如下图:
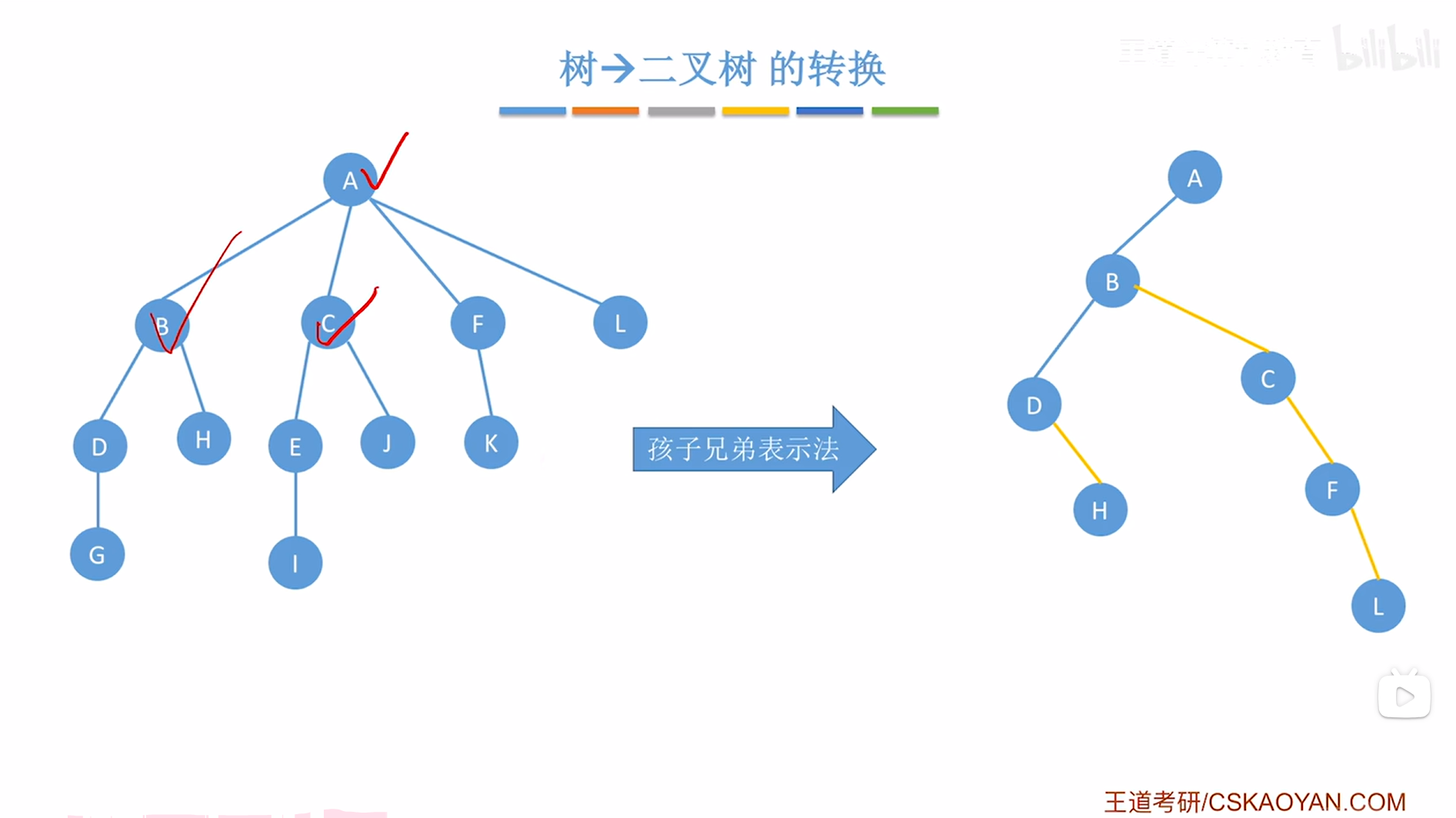
如上图,
B结点处理完毕,接下来需要按"树的层序"依次处理每个结点,因此接下来处理C结点,
首先要观察当前处理的结点即C在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于C结点来说,他有E、J两个孩子,因此需要把E、J用右指针串成一个"冰糖葫芦"的形态,
如下图:
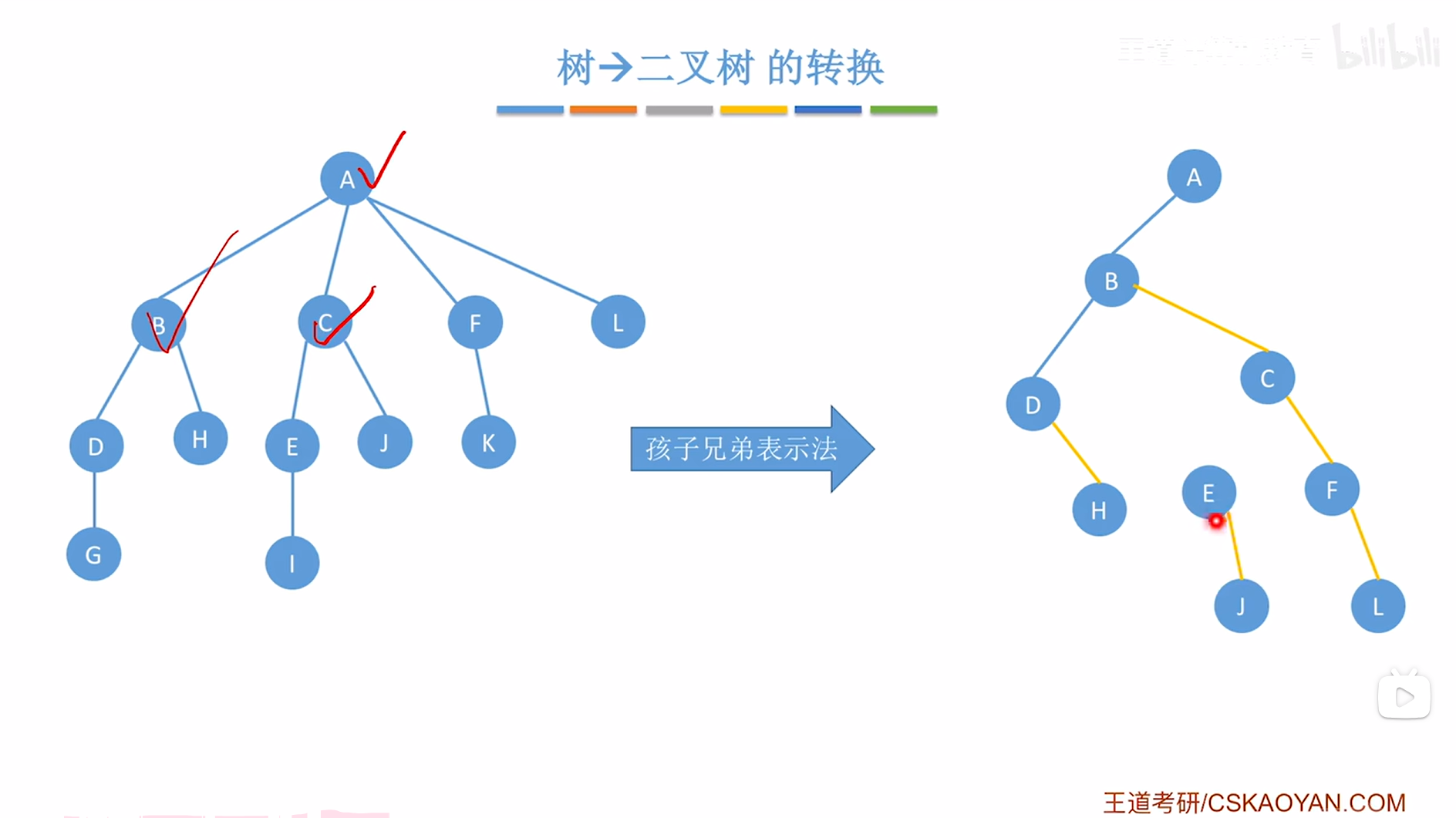
如上图,
接下来要在创建的二叉树中把C结点的第一个孩子即E挂在当前处理的结点即C的左指针上,
如下图:
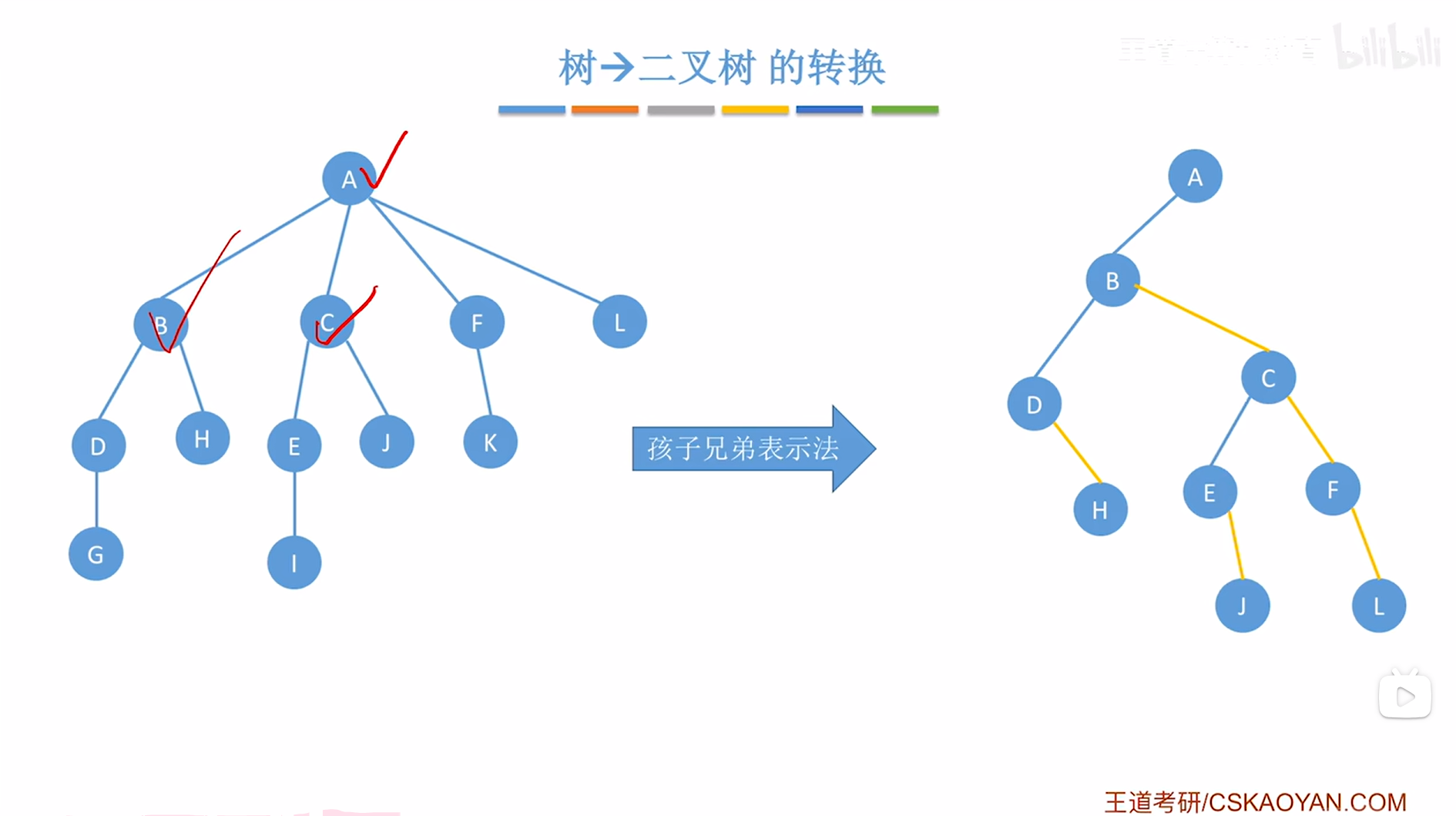
如上图,
C结点处理完毕,接下来需要按"树的层序"依次处理每个结点,因此接下来处理F结点,
首先要观察当前处理的结点即F在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于F结点来说,他只有一个孩子即K结点,
因此接下来要在创建的二叉树中把F结点的第一个孩子即K挂在当前处理的结点即F的左指针上,
如下图:
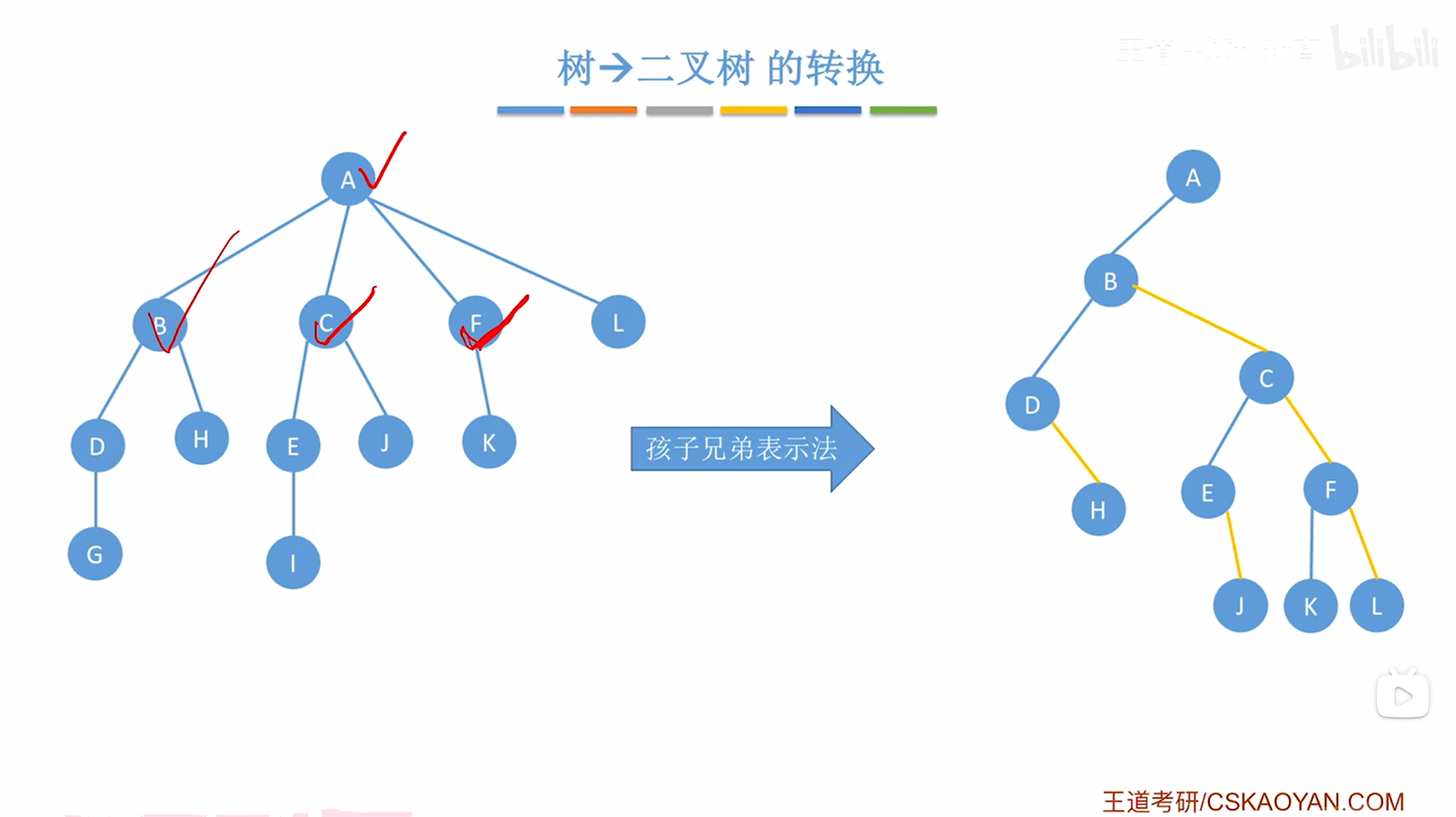
如上图,
F结点处理完毕,接下来需要按"树的层序"依次处理每个结点,因此接下来处理L结点,
首先要观察当前处理的结点即L在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于L结点来说,L结点没有孩子,所以不需要处理,
如下图:
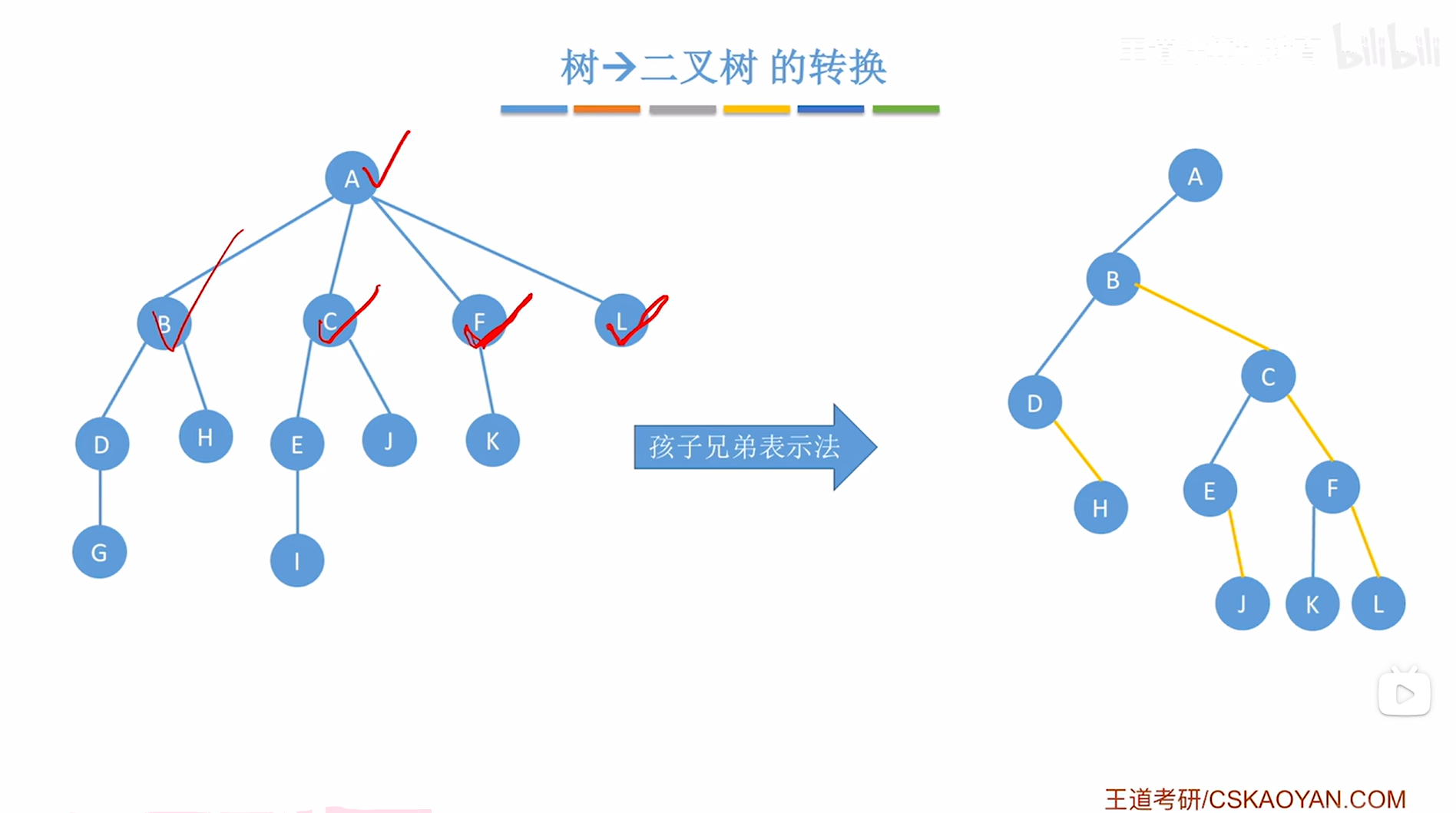
如上图,
L结点处理完毕,接下来需要按"树的层序"依次处理每个结点,因此接下来处理D结点,
首先要观察当前处理的结点即D在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于D结点来说,他只有一个孩子即G结点,
因此接下来要在创建的二叉树中把D结点的第一个孩子即G挂在当前处理的结点即D的左指针上,
如下图:
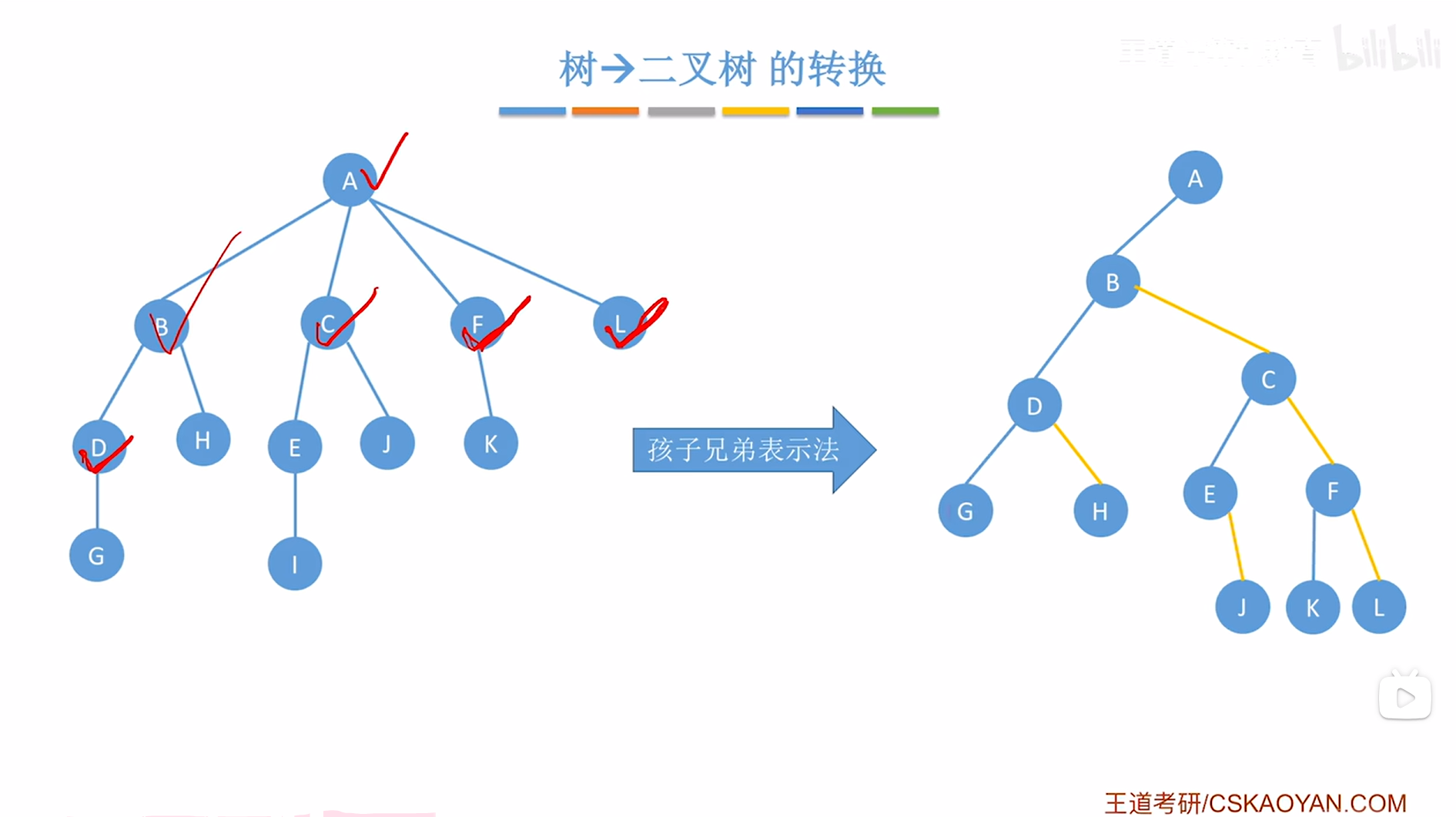
如上图,
D结点处理完毕,接下来需要按"树的层序"依次处理每个结点,因此接下来处理H结点,
首先要观察当前处理的结点即H在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于H结点来说,H结点没有孩子,所以不需要处理,
如下图:
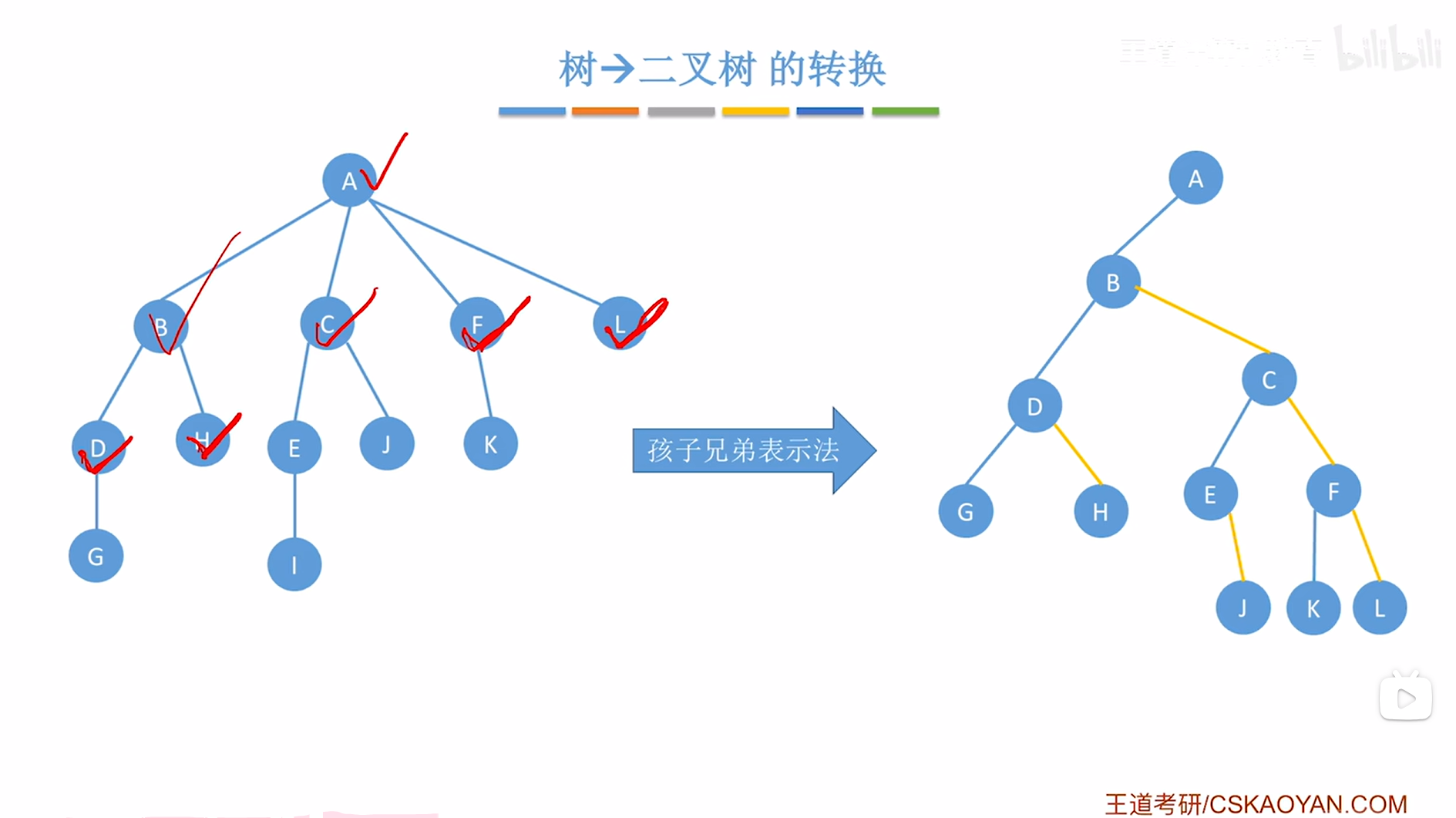
如上图,
H结点处理完毕,接下来需要按"树的层序"依次处理每个结点,因此接下来处理E结点,
首先要观察当前处理的结点即E在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于E结点来说,他只有一个孩子即I结点,
因此接下来要在创建的二叉树中把E结点的第一个孩子即I挂在当前处理的结点即E的左指针上,
如下图:
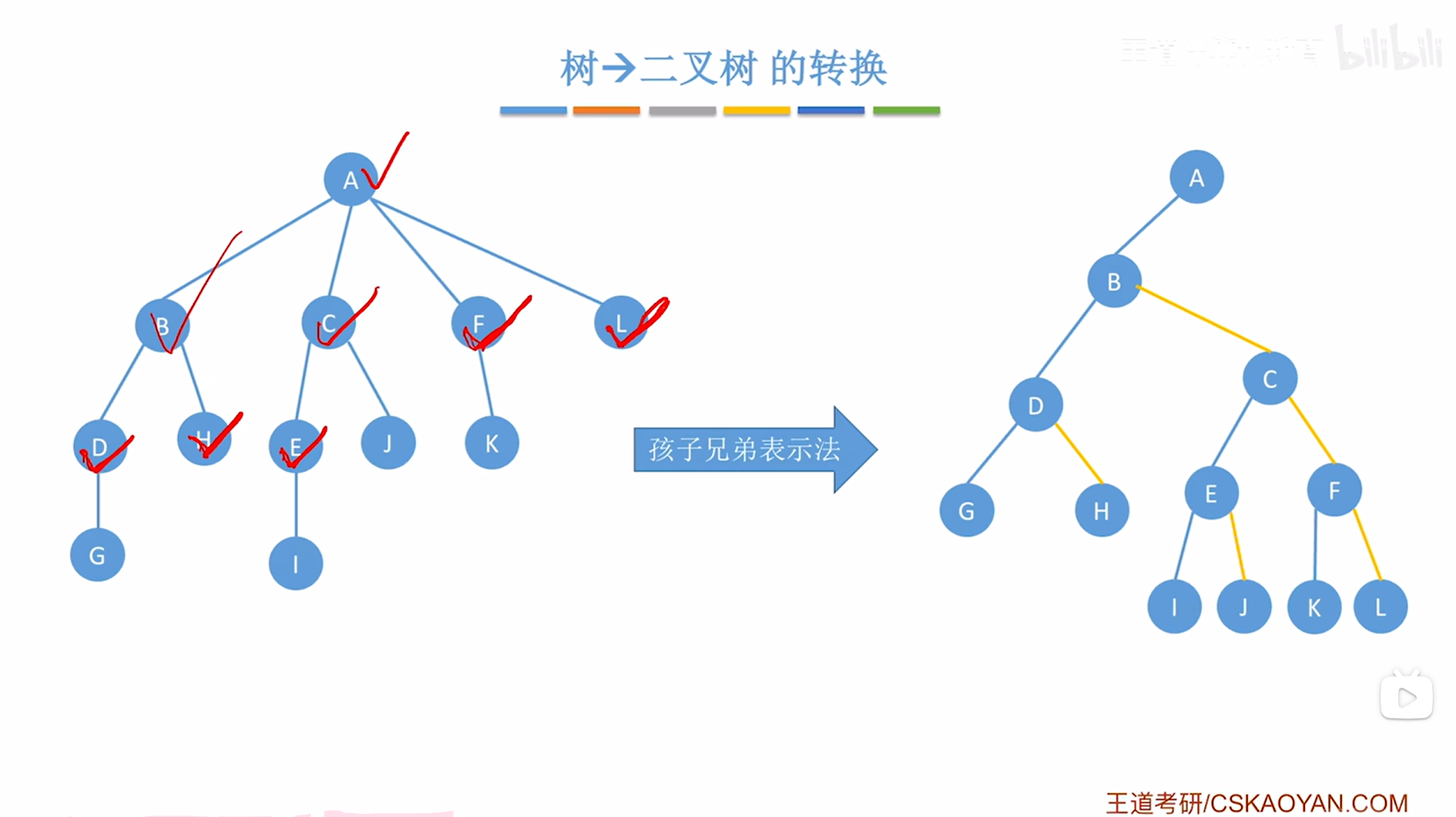
如上图,
E结点处理完毕,接下来按照"树的层序"应该依次处理J、K、G、I结点,同理,
首先要观察当前处理的结点在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于J、K、G、I结点来说,显然都没有孩子,所以J、K、G、I结点都不需要做任何处理,
至此,就完成了"树->二叉树"的转换,
如下图:
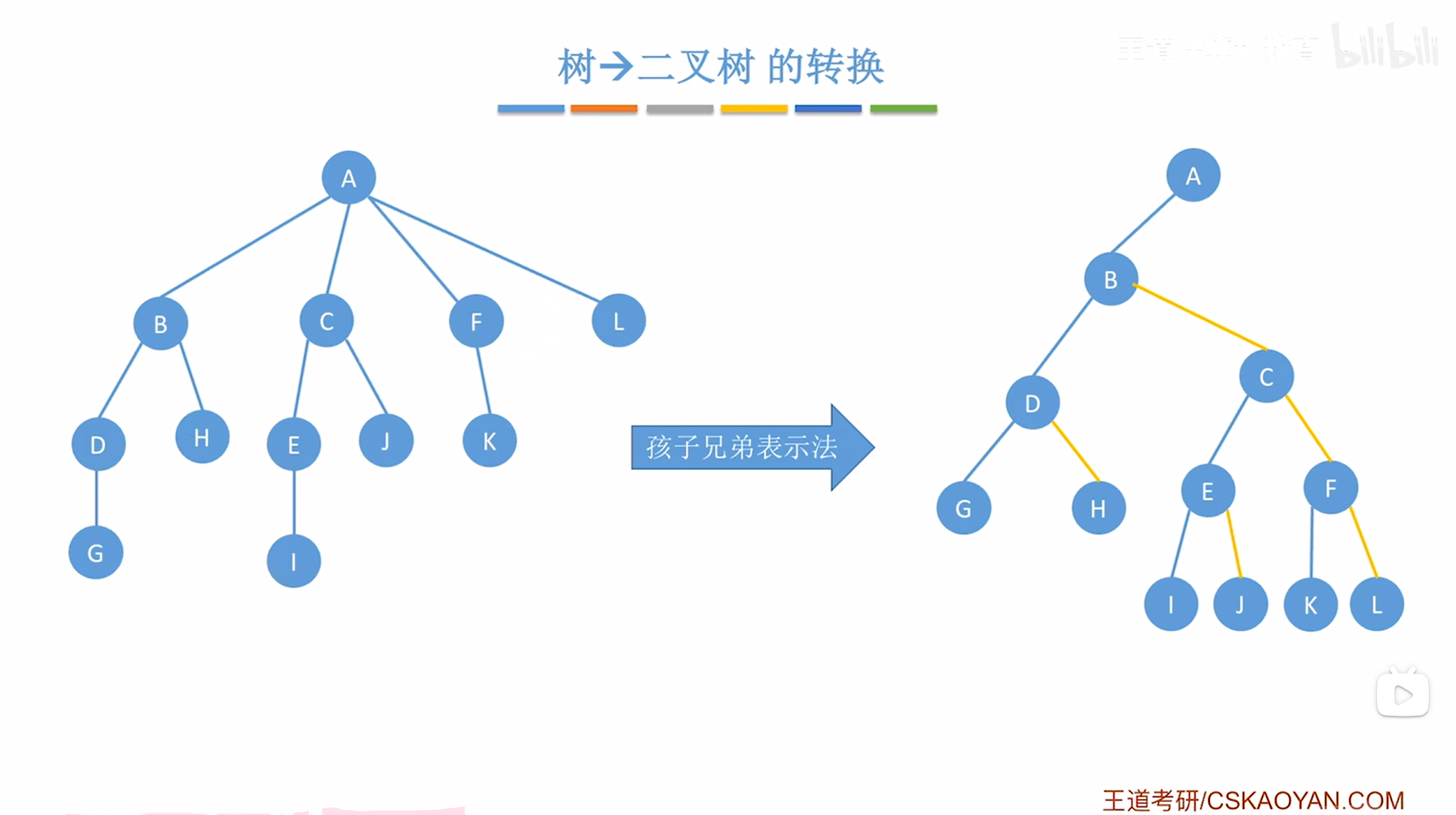
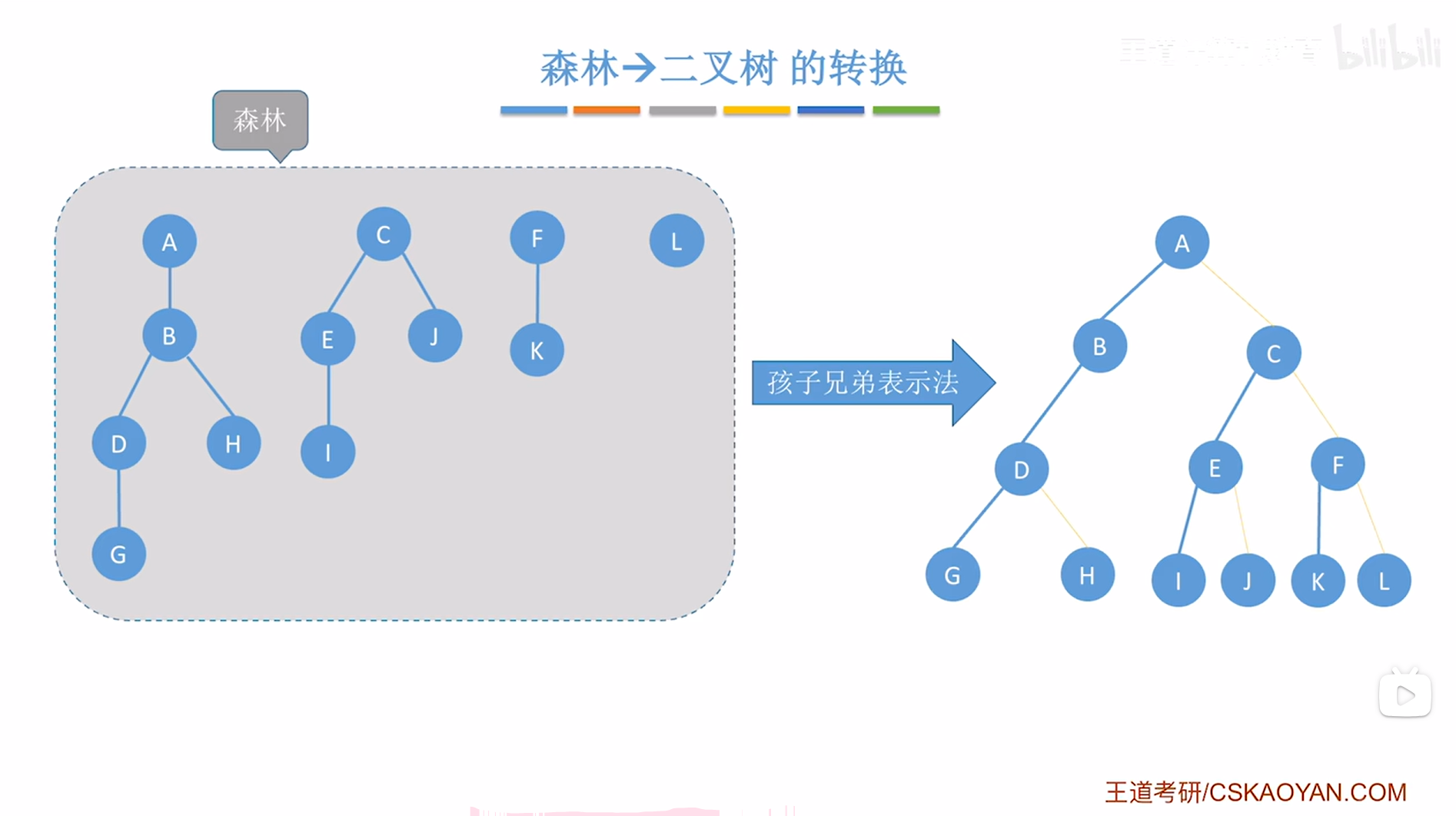
二."森林->二叉树"的转换:
1.例一:
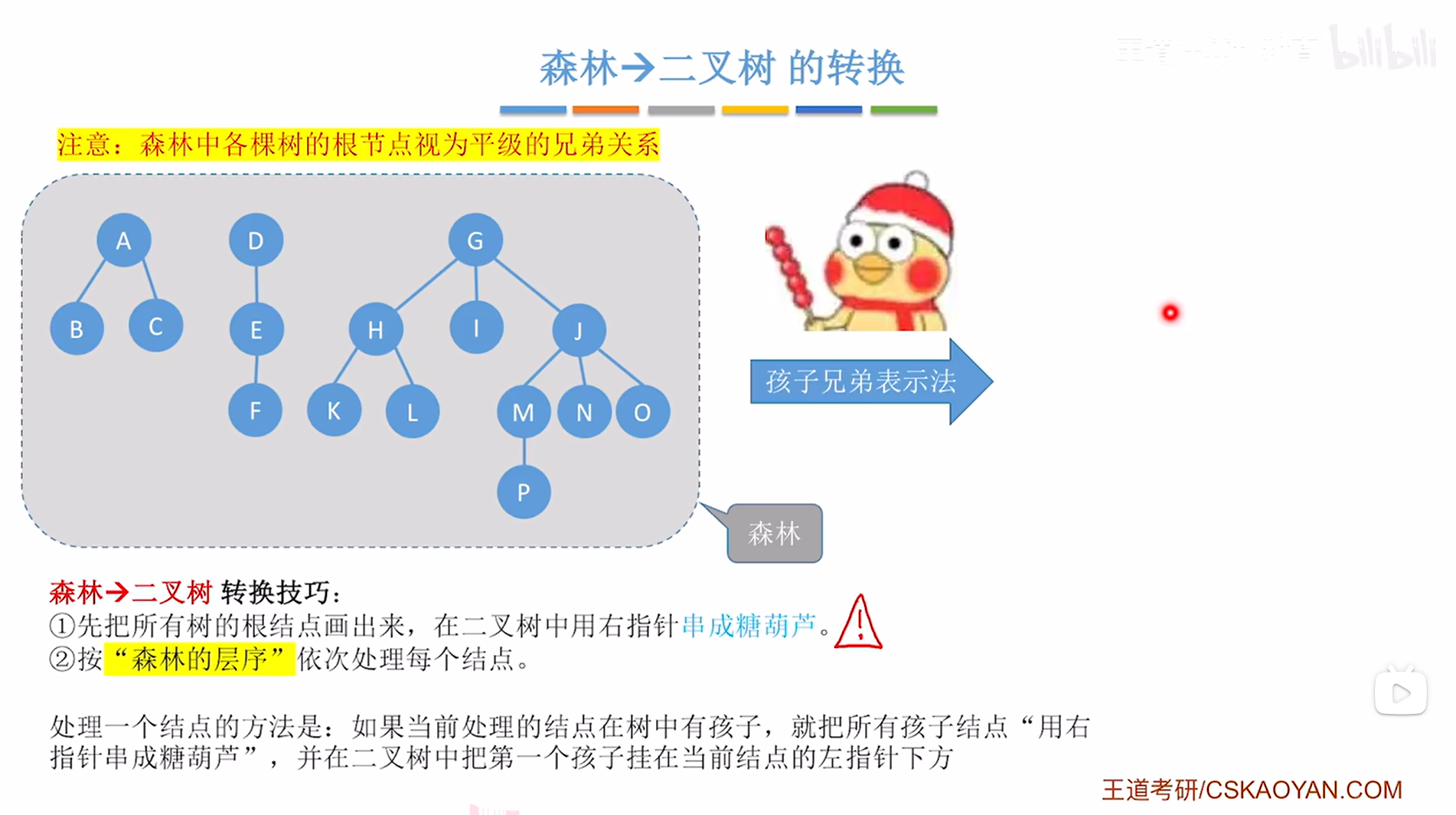
如上图,
"森林->二叉树"的转换思路与"树->二叉树"的转换思路类似,
唯一需要注意的是第一步中树只有1个根结点,而森林至少有2两个平级的根结点,
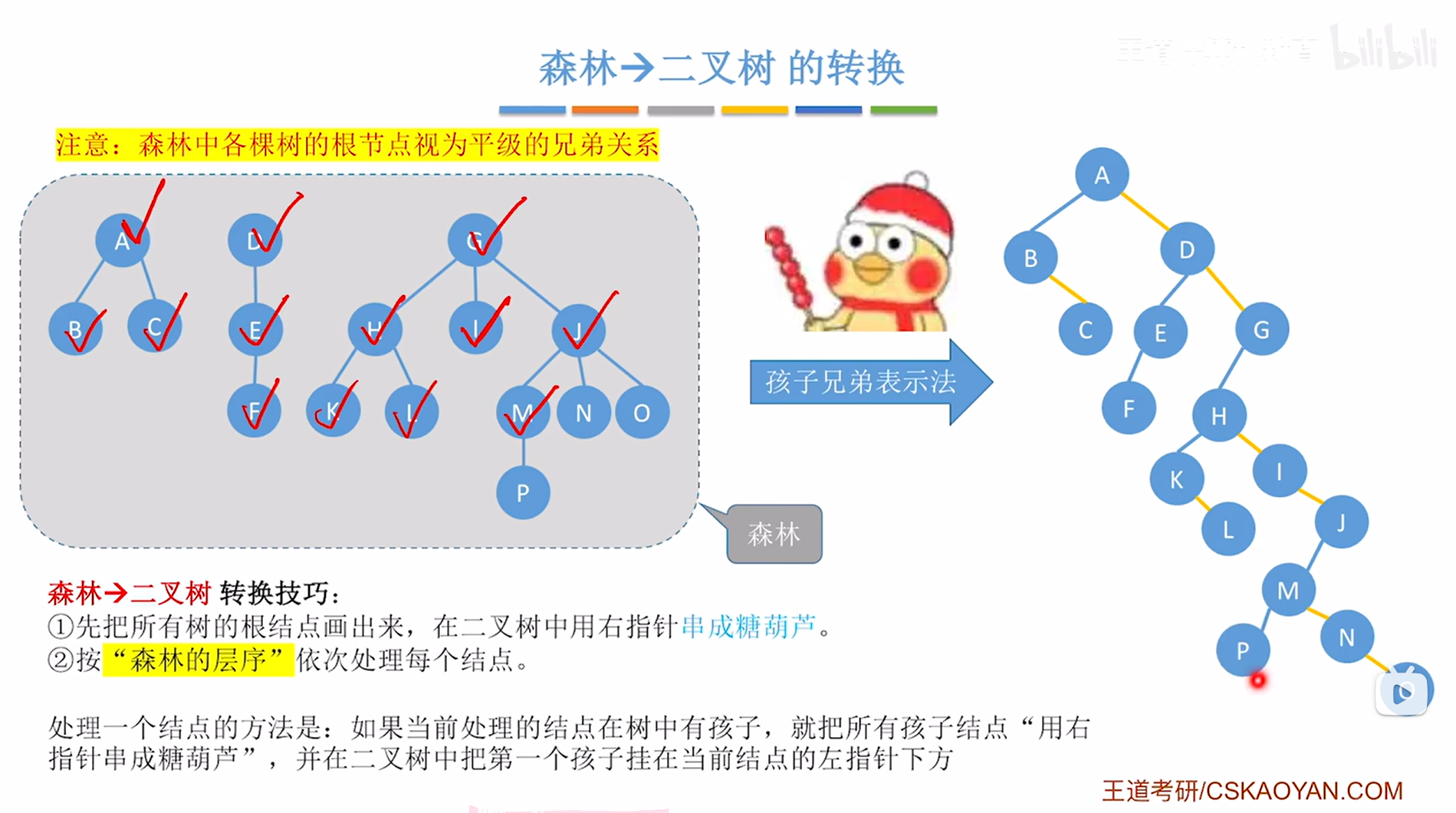
森林中所有的根结点视为平级的兄弟结点,
所以森林转换为二叉树的时候,第一步需要把森林中所有的根结点用右指针"串成糖葫芦",
本例中森林的根结点为A、D、G,
如下图:
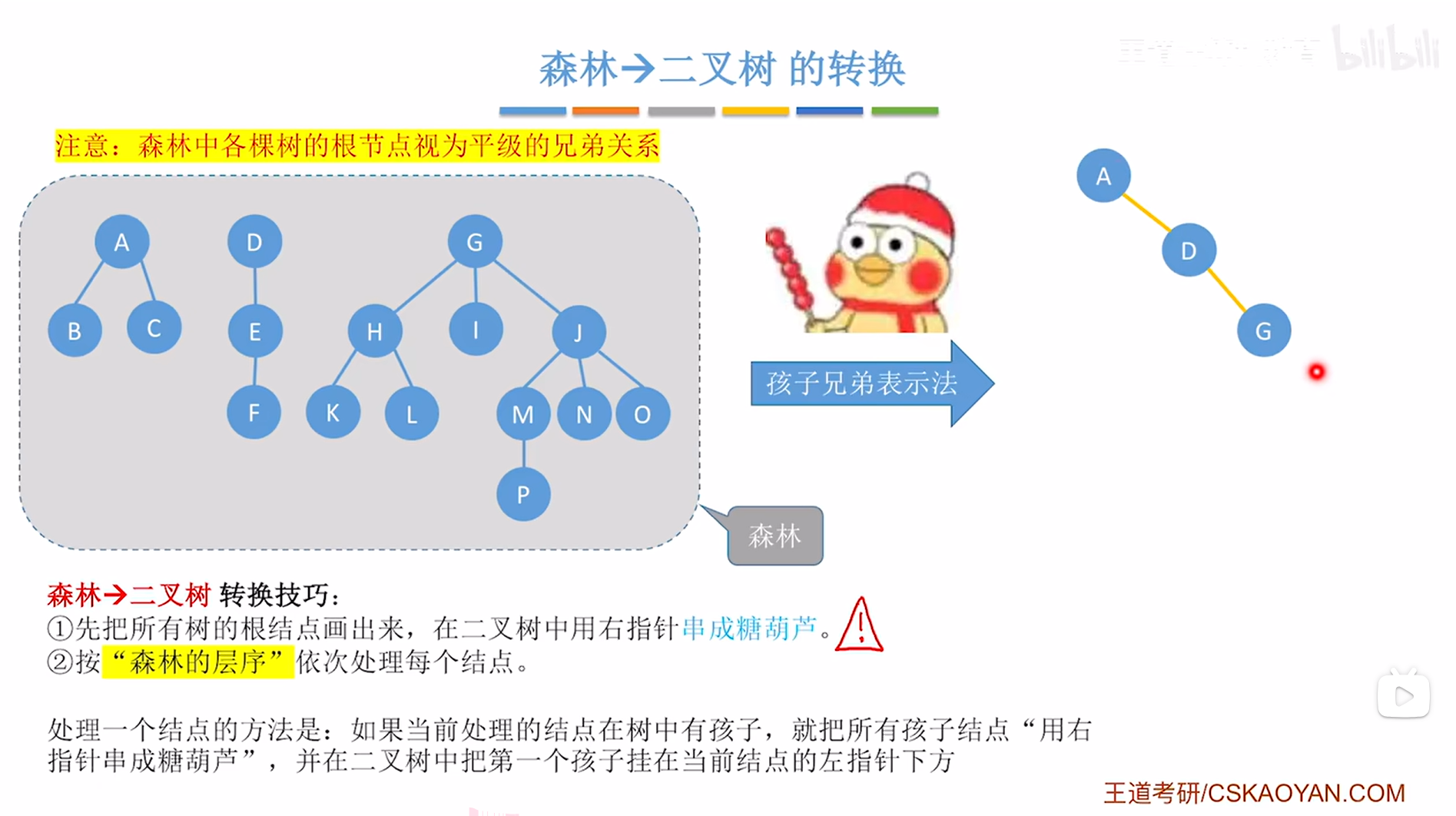
如上图,
接下来按照"森林的层序"依次处理每个结点,"森林的层序"就是指把整个森林看作一个整体,
第一层就是A、D、G,第二层就是B、C、E、H、I、J,第三层就是F、K、L、M、N、O,第四层就是P,因此处理顺序就是A->D->G->B->C->E->H->I->J->F->K->L->M->N->O->P,
首先处理树中第一层的A,处理的方法如下:
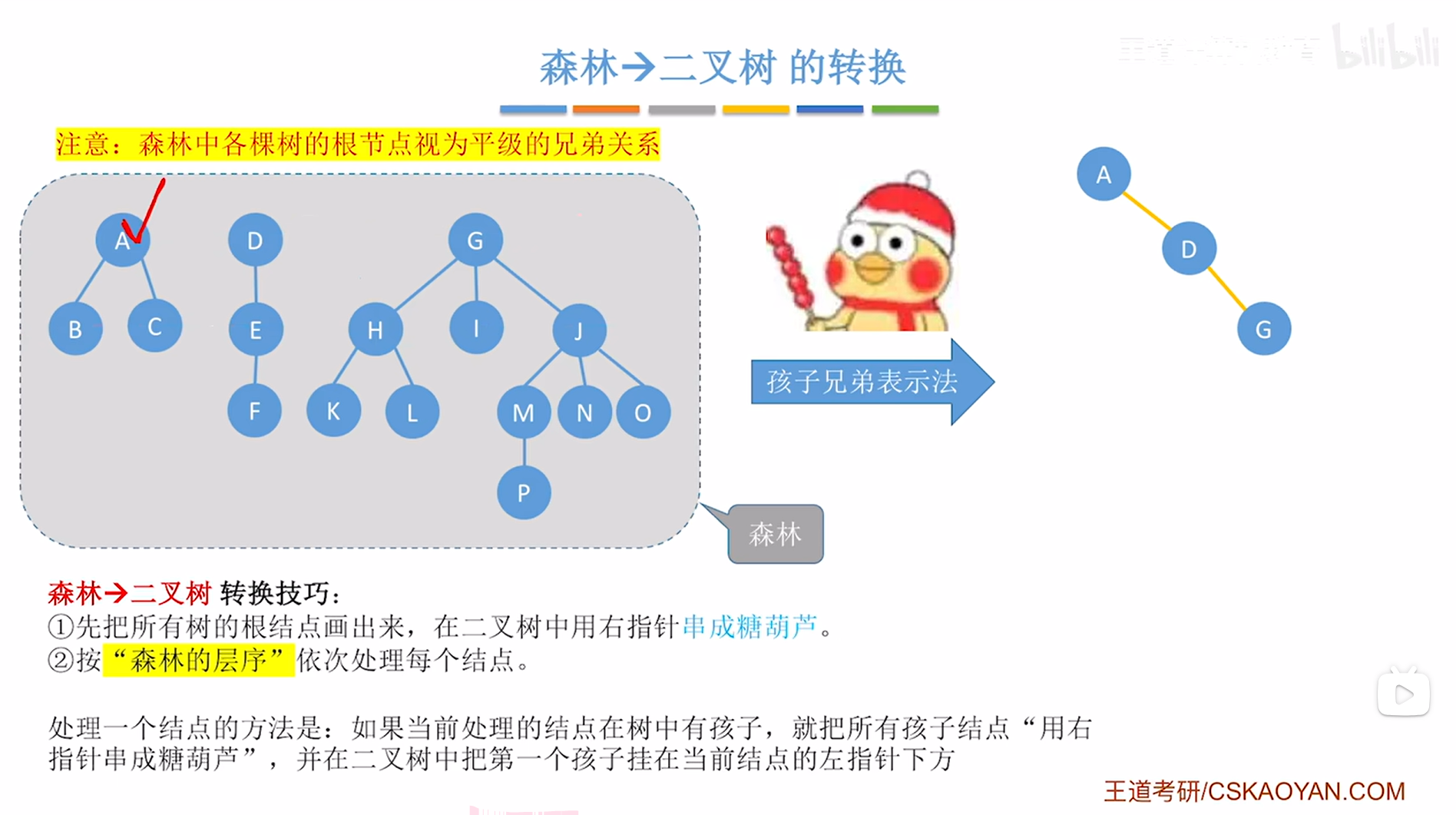
如上图,
首先要观察当前处理的结点即A在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于A结点来说,他有B、C两个孩子,因此需要把B、C用右指针串成一个"冰糖葫芦"的形态,
如下图:
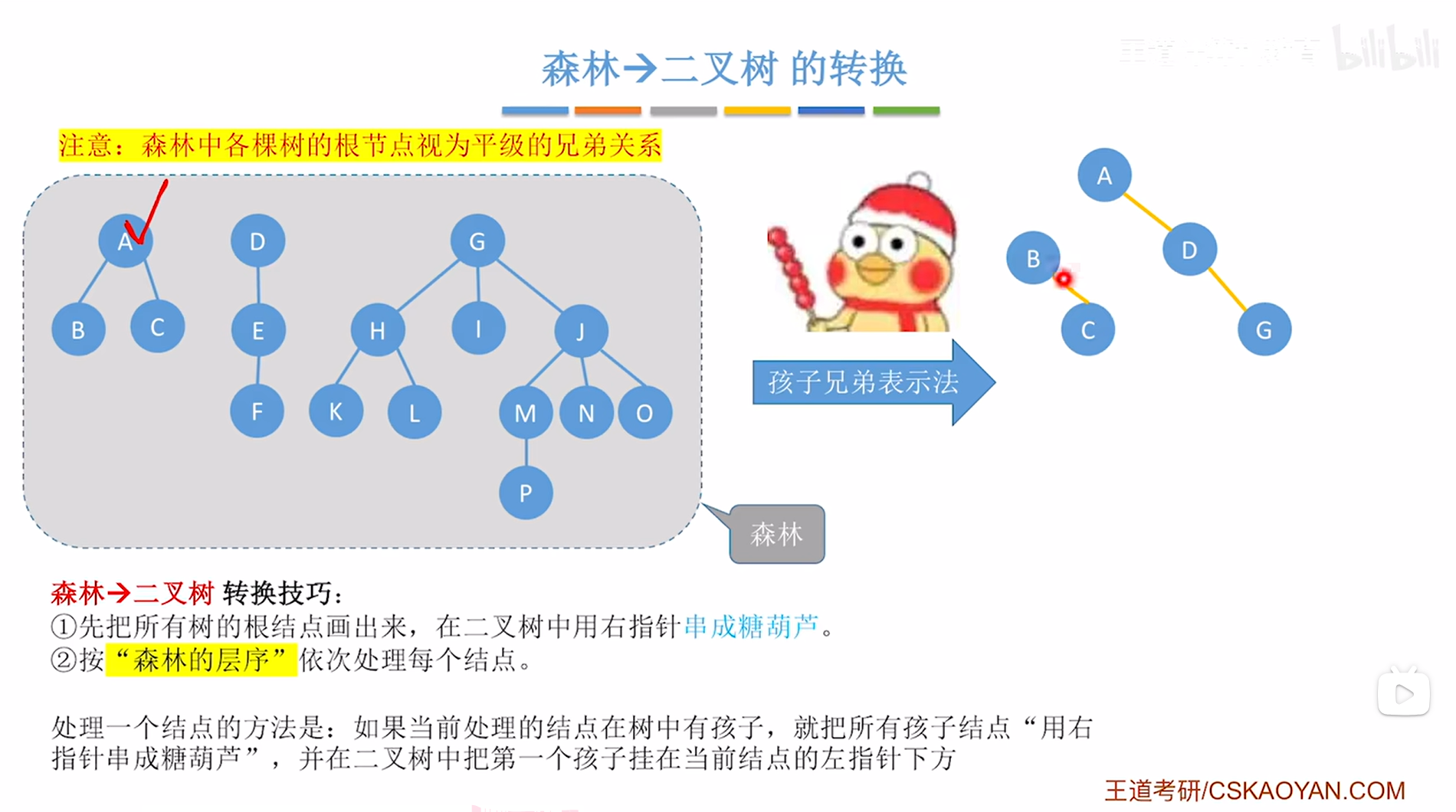
如上图,
接下来要在创建的二叉树中把A结点的第一个孩子即B挂在当前处理的结点即A的左指针上,
如下图:
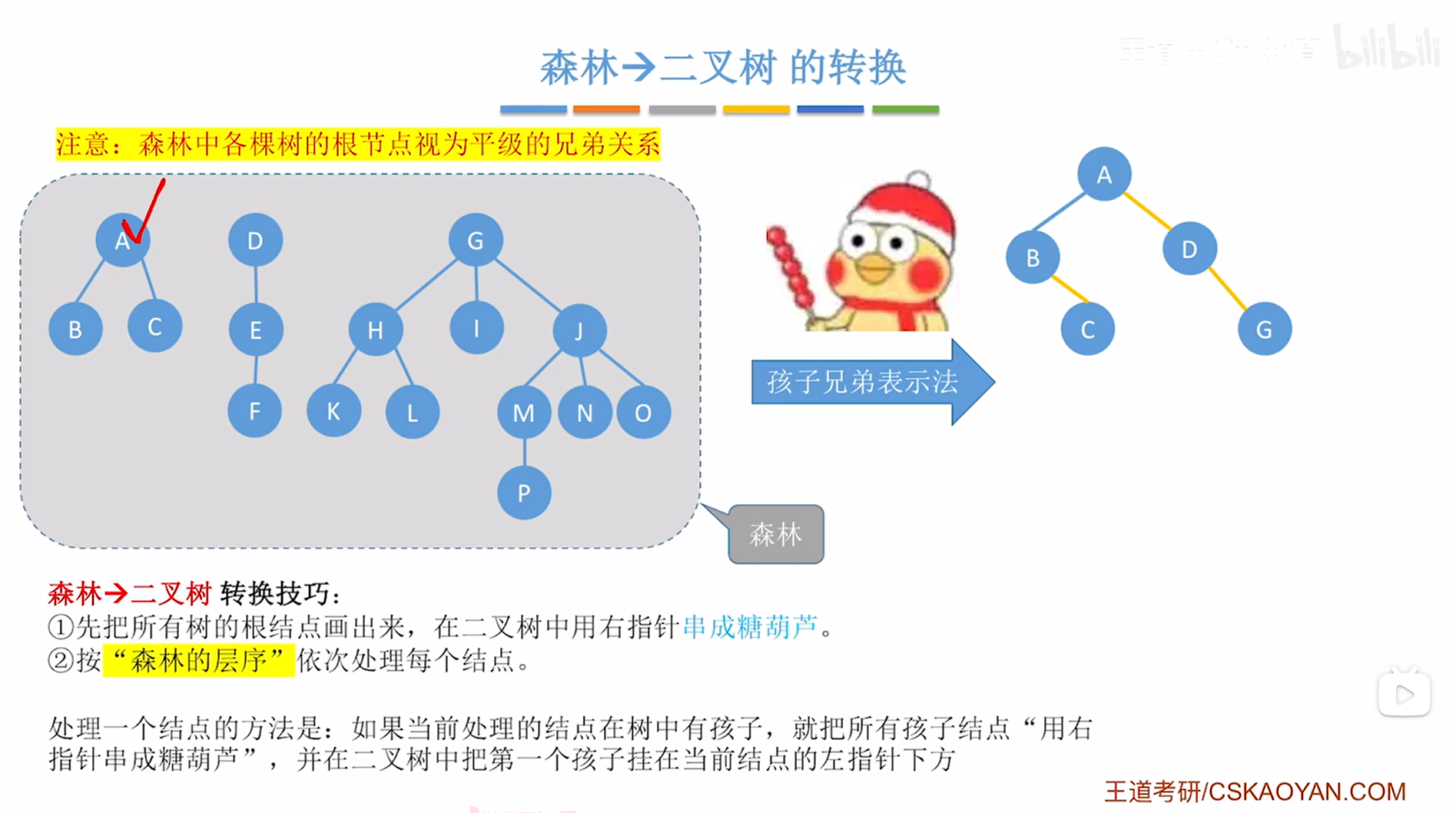
如上图,
A结点处理完毕,接下来需要按"树的层序"依次处理每个结点,因此接下来处理D结点,
首先要观察当前处理的结点即D在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于D结点来说,他只有一个孩子即E结点,
因此接下来要在创建的二叉树中把D结点的第一个孩子即E挂在当前处理的结点即D的左指针上,
如下图:
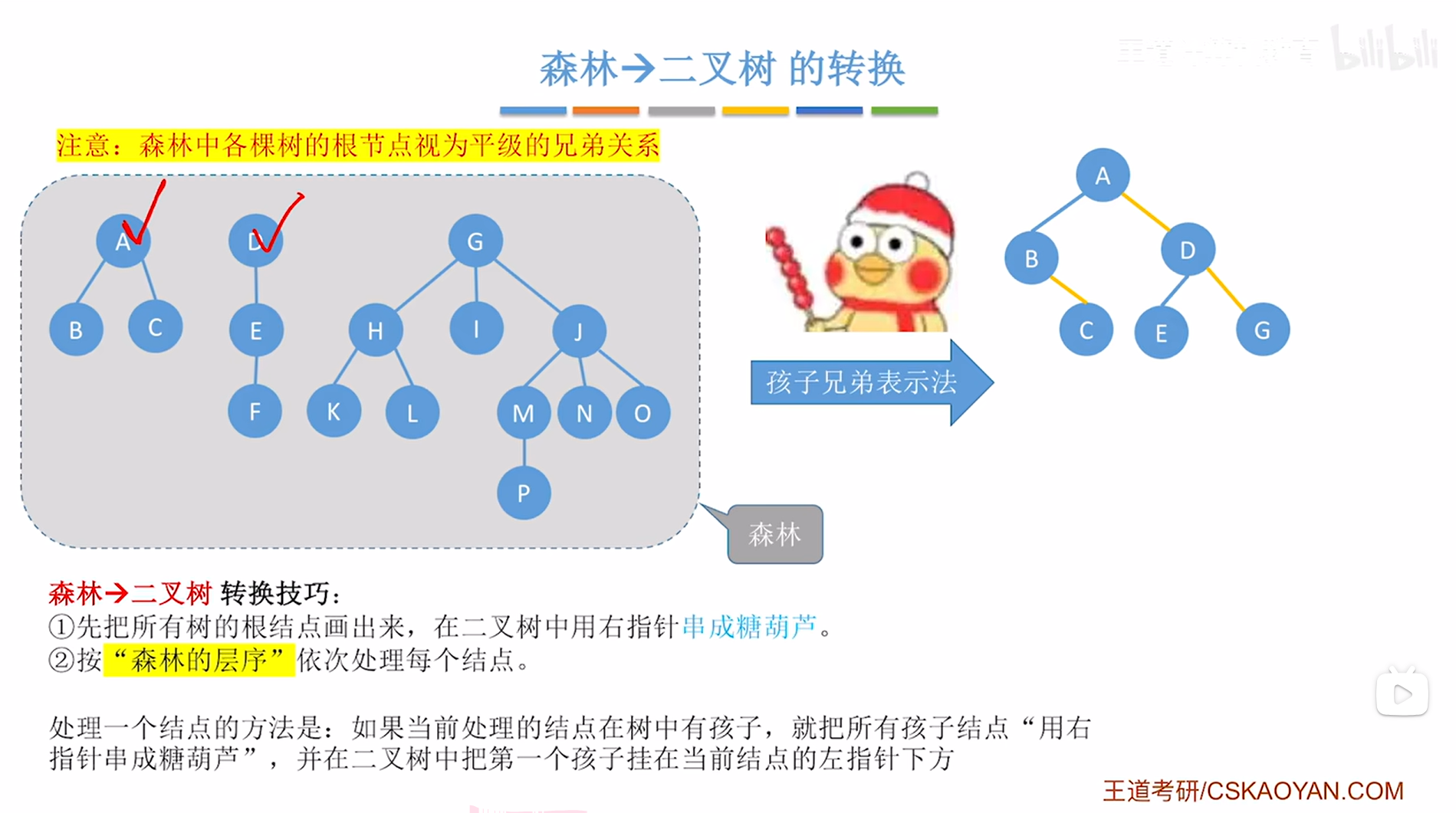
如上图,
D结点处理完毕,接下来需要按"树的层序"依次处理每个结点,因此接下来处理G结点,
首先要观察当前处理的结点即G在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于G结点来说,他有H、I、J三个孩子,因此需要把H、I、J用右指针串成一个"冰糖葫芦"的形态,
如下图:
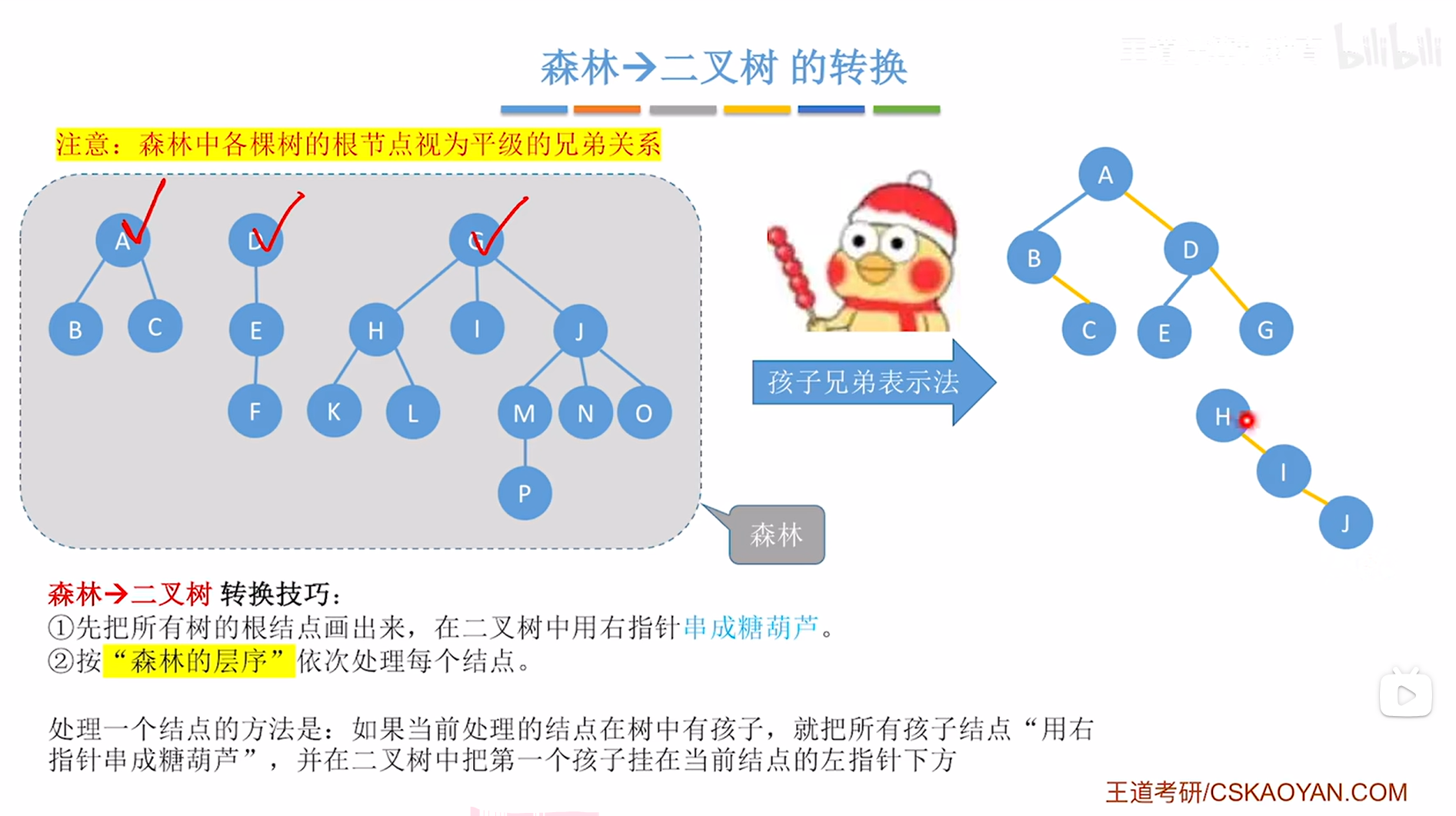
如上图,
接下来要在创建的二叉树中把G结点的第一个孩子即H挂在当前处理的结点即G的左指针上,
如下图:
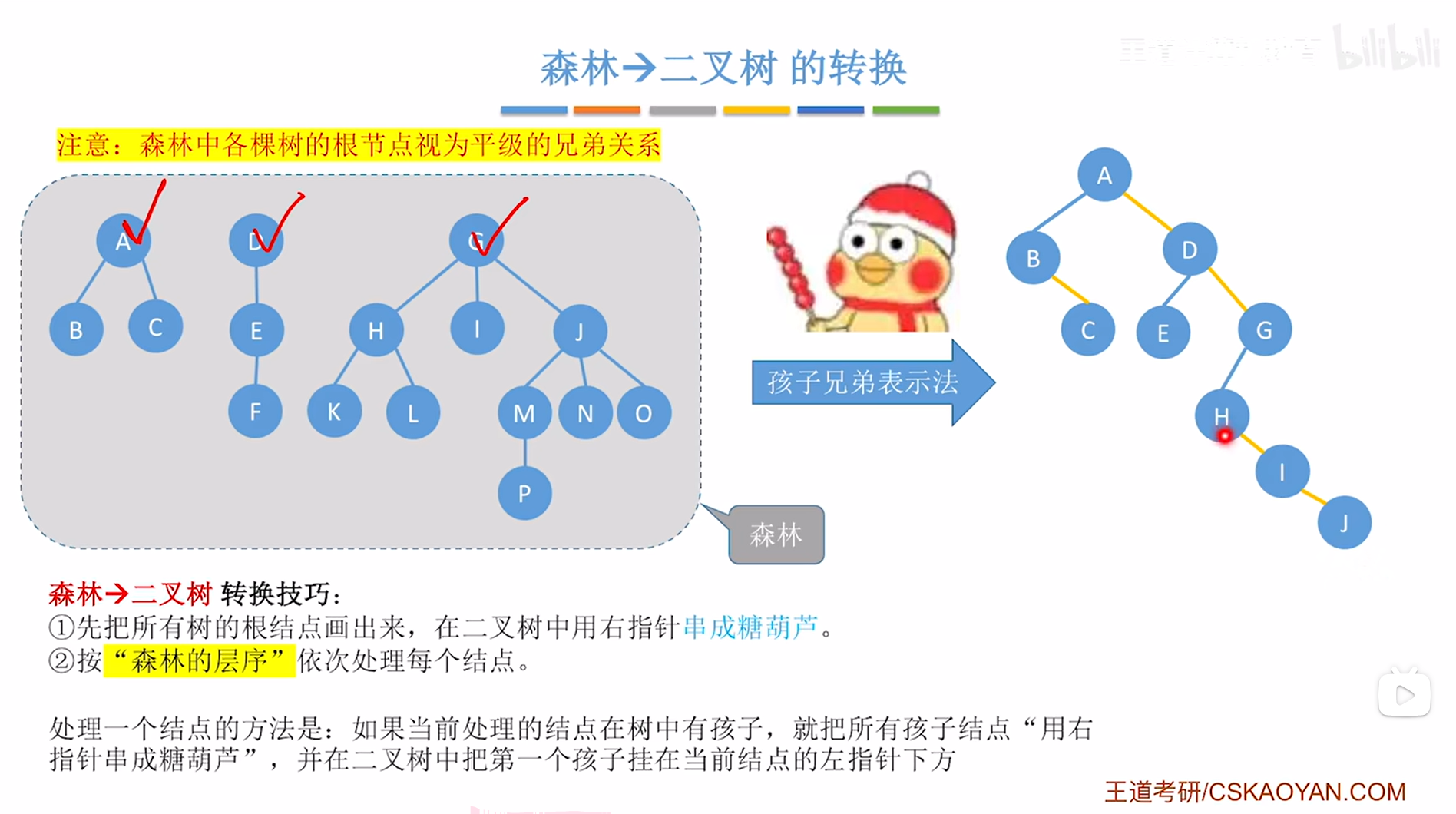
如上图,
G结点处理完毕,接下来按照"树的层序"应该依次处理B、C结点,同理,
首先要观察当前处理的结点在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于B、C结点来说,显然都没有孩子,所以B、C结点都不需要做任何处理;
B、C结点处理完毕,接下来需要按"树的层序"依次处理每个结点,因此接下来处理E结点,
首先要观察当前处理的结点即E在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于E结点来说,他只有一个孩子即F结点,
因此接下来要在创建的二叉树中把E结点的第一个孩子即F挂在当前处理的结点即E的左指针上,
如下图:
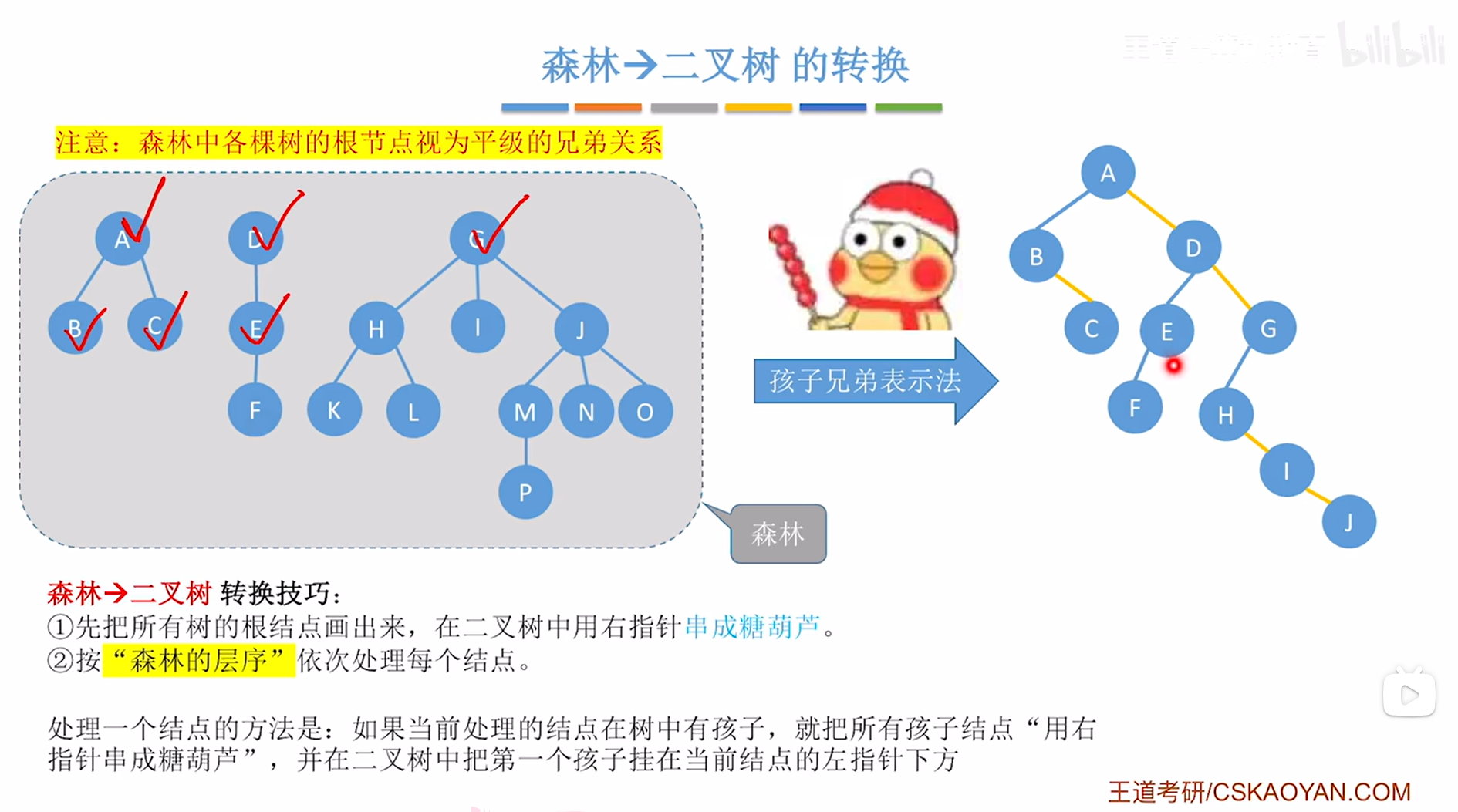
如上图,
E结点处理完毕,接下来需要按"树的层序"依次处理每个结点,因此接下来处理H结点,
首先要观察当前处理的结点即H在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于H结点来说,他有K、L两个孩子,因此需要把K、L用右指针串成一个"冰糖葫芦"的形态,
如下图:
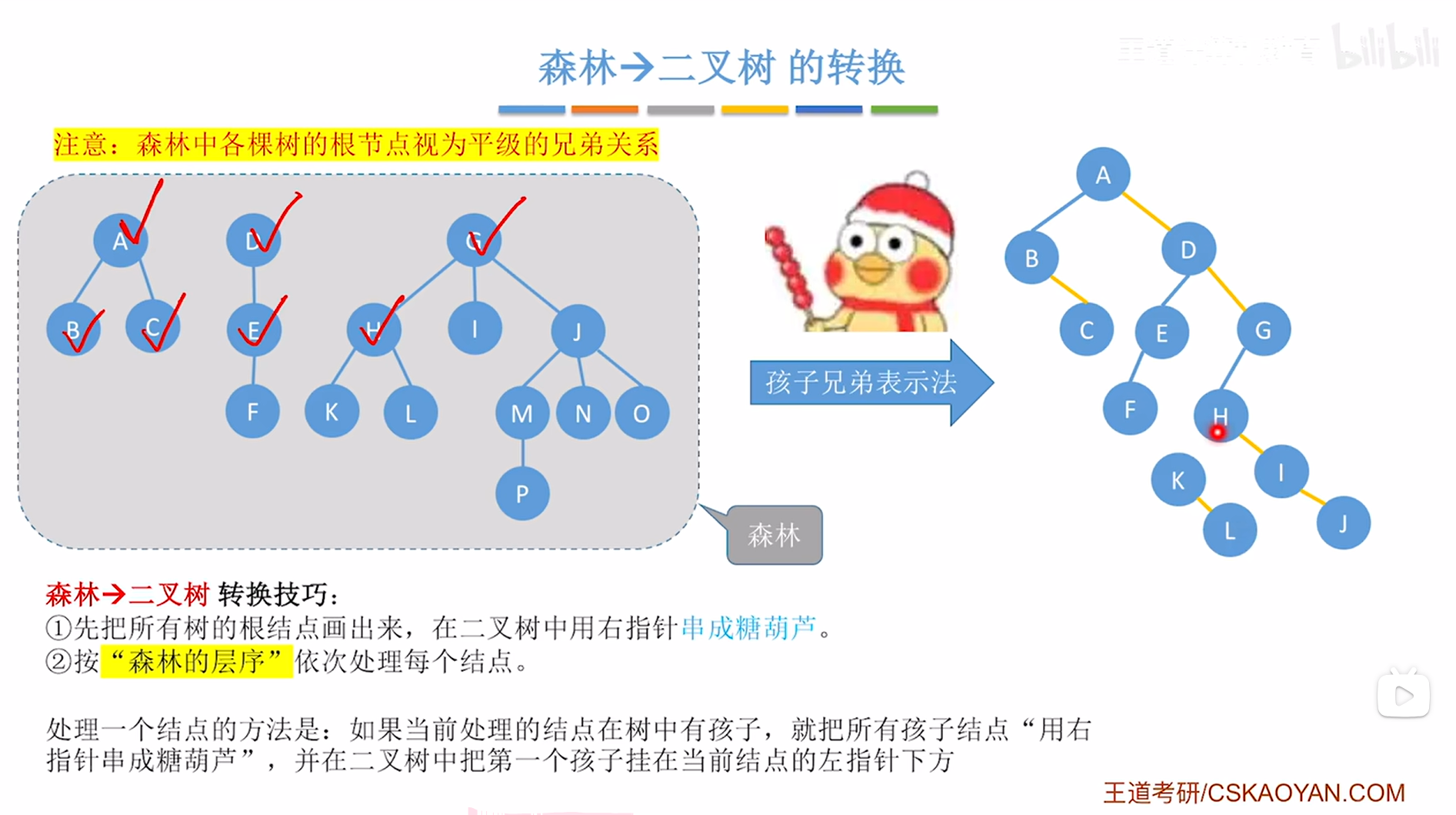
如上图,
接下来要在创建的二叉树中把H结点的第一个孩子即K挂在当前处理的结点即H的左指针上,
如下图:
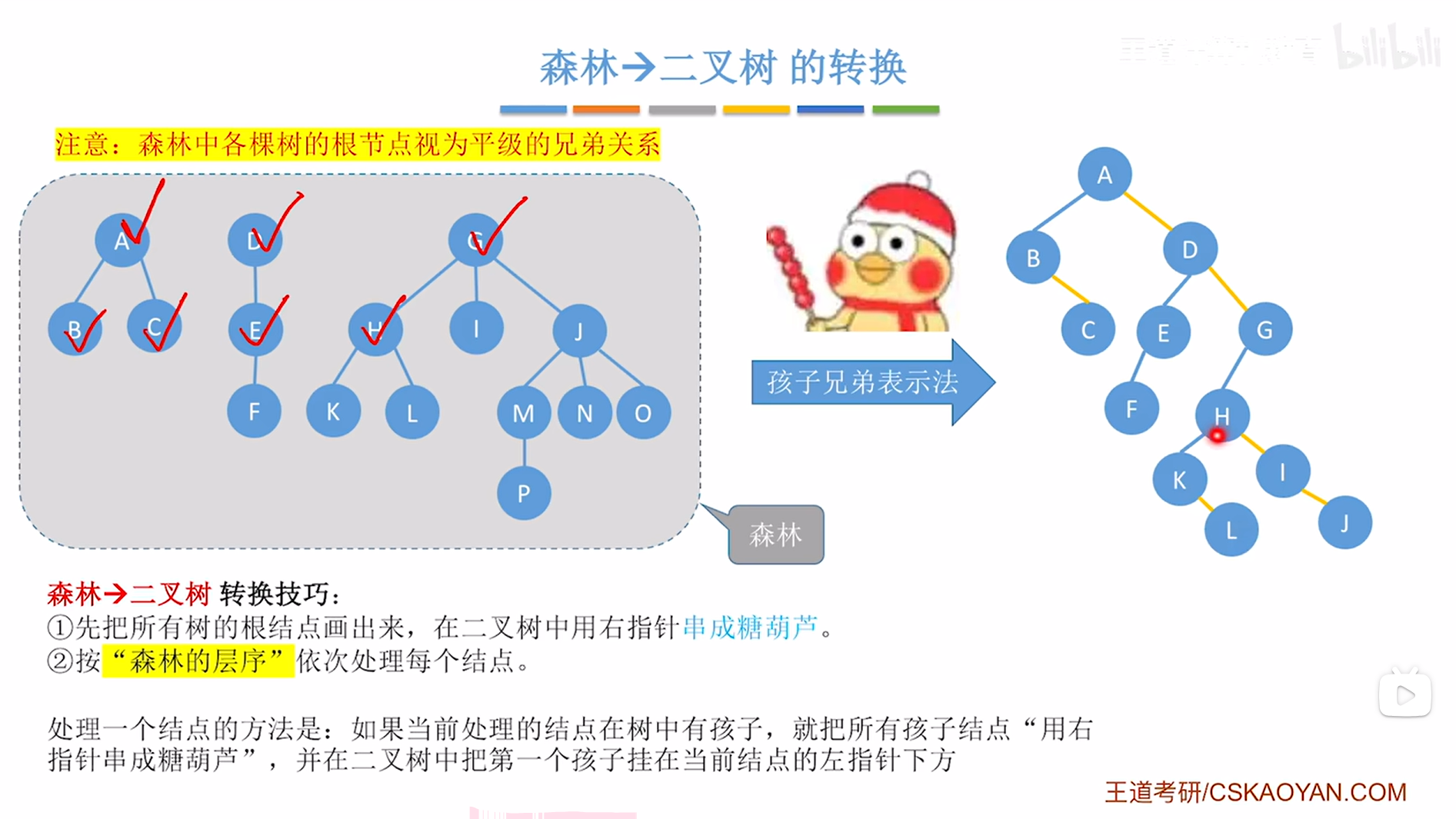
如上图,
H结点处理完毕,接下来按照"树的层序"应该处理I结点,同理,
首先要观察当前处理的结点即I在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于I结点来说,显然都没有孩子,所以I结点都不需要做任何处理;
I结点处理完毕,接下来需要按"树的层序"依次处理每个结点,因此接下来处理J结点,
首先要观察当前处理的结点即J在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于J结点来说,他有M、N、O三个孩子,因此需要把M、N、O用右指针串成一个"冰糖葫芦"的形态,
如下图:
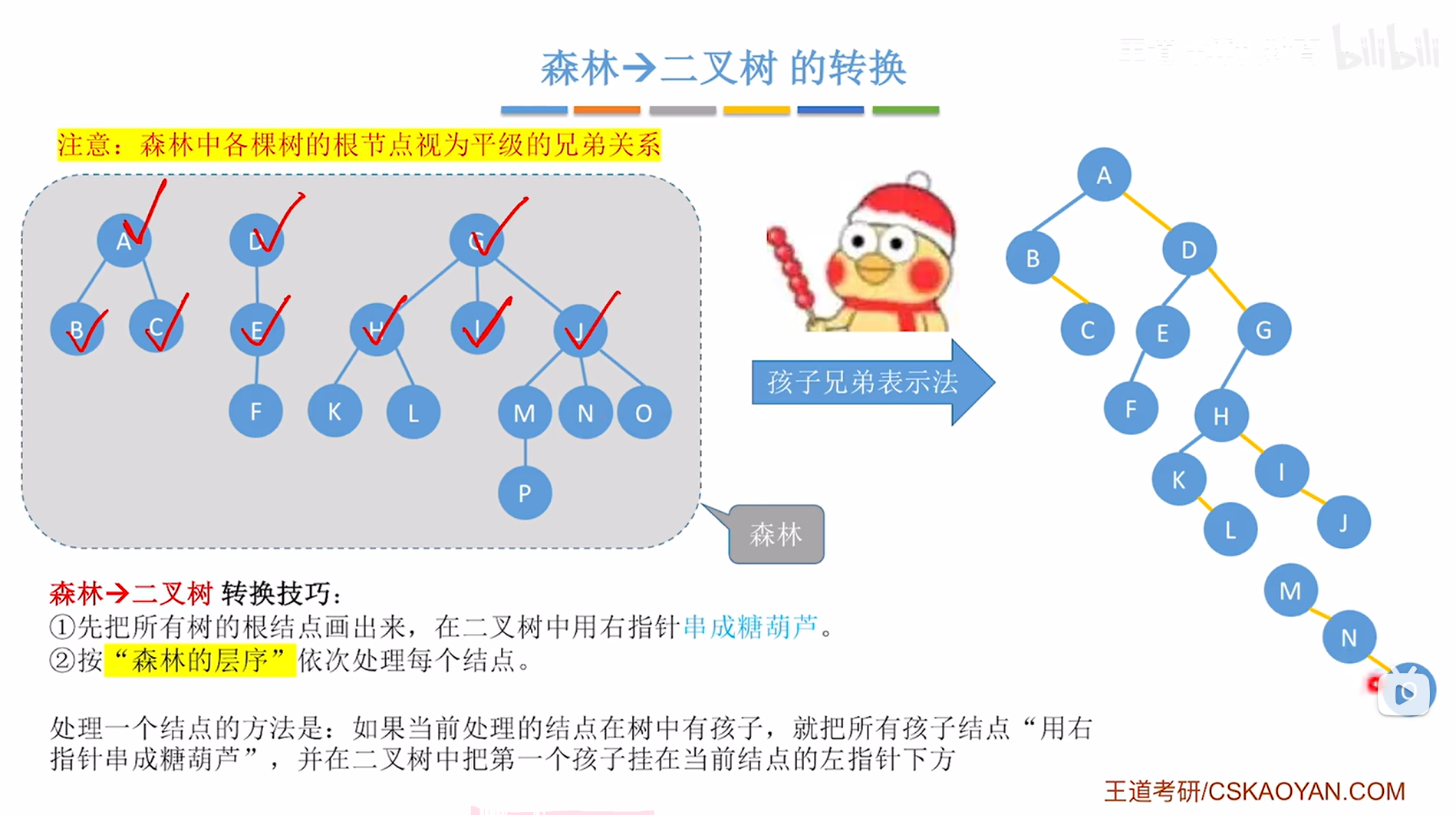
如上图,
接下来要在创建的二叉树中把J结点的第一个孩子即M挂在当前处理的结点即J的左指针上,
如下图:
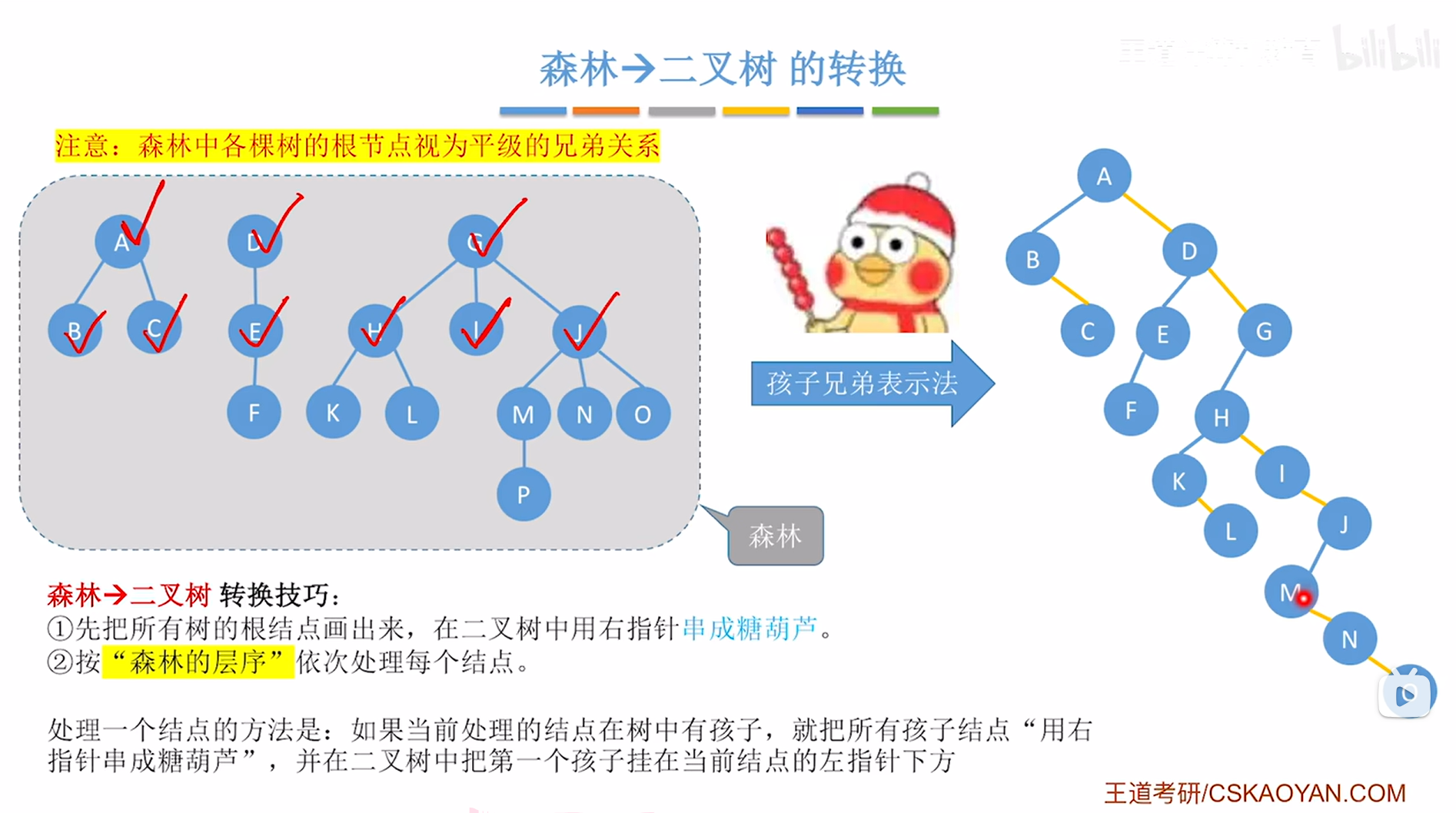
上图,
J结点处理完毕,接下来按照"树的层序"应该依次处理F、K、L结点,同理,
首先要观察当前处理的结点在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于F、K、L结点来说,显然都没有孩子,所以F、K、L结点都不需要做任何处理;
F、K、L结点处理完毕,接下来需要按"树的层序"依次处理每个结点,因此接下来处理M结点,
首先要观察当前处理的结点即M在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于M结点来说,他只有一个孩子即P结点,
因此接下来要在创建的二叉树中把M结点的第一个孩子即P挂在当前处理的结点即M的左指针上,
如下图:
如上图,
M结点处理完毕,接下来按照"树的层序"应该依次处理N、O、P结点,同理,
首先要观察当前处理的结点在树中是否有孩子,如果有孩子,那么就要把它所有的孩子"用右指针串成糖葫芦",
对于N、O、P结点来说,显然都没有孩子,所以N、O、P结点都不需要做任何处理,
至此,就完成了"森林->二叉树"的转换,
如下图:
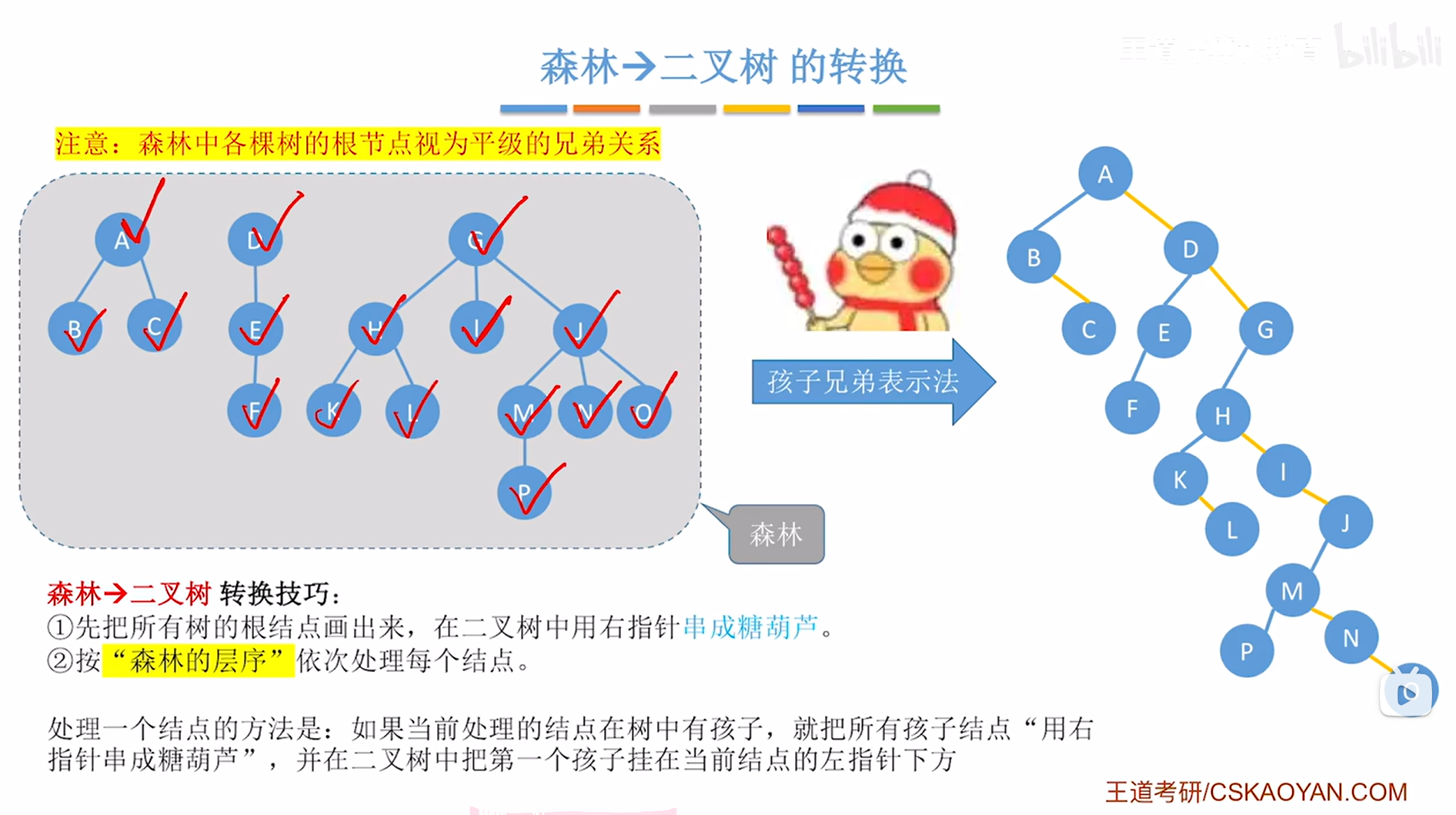
2.例二:原理同例一
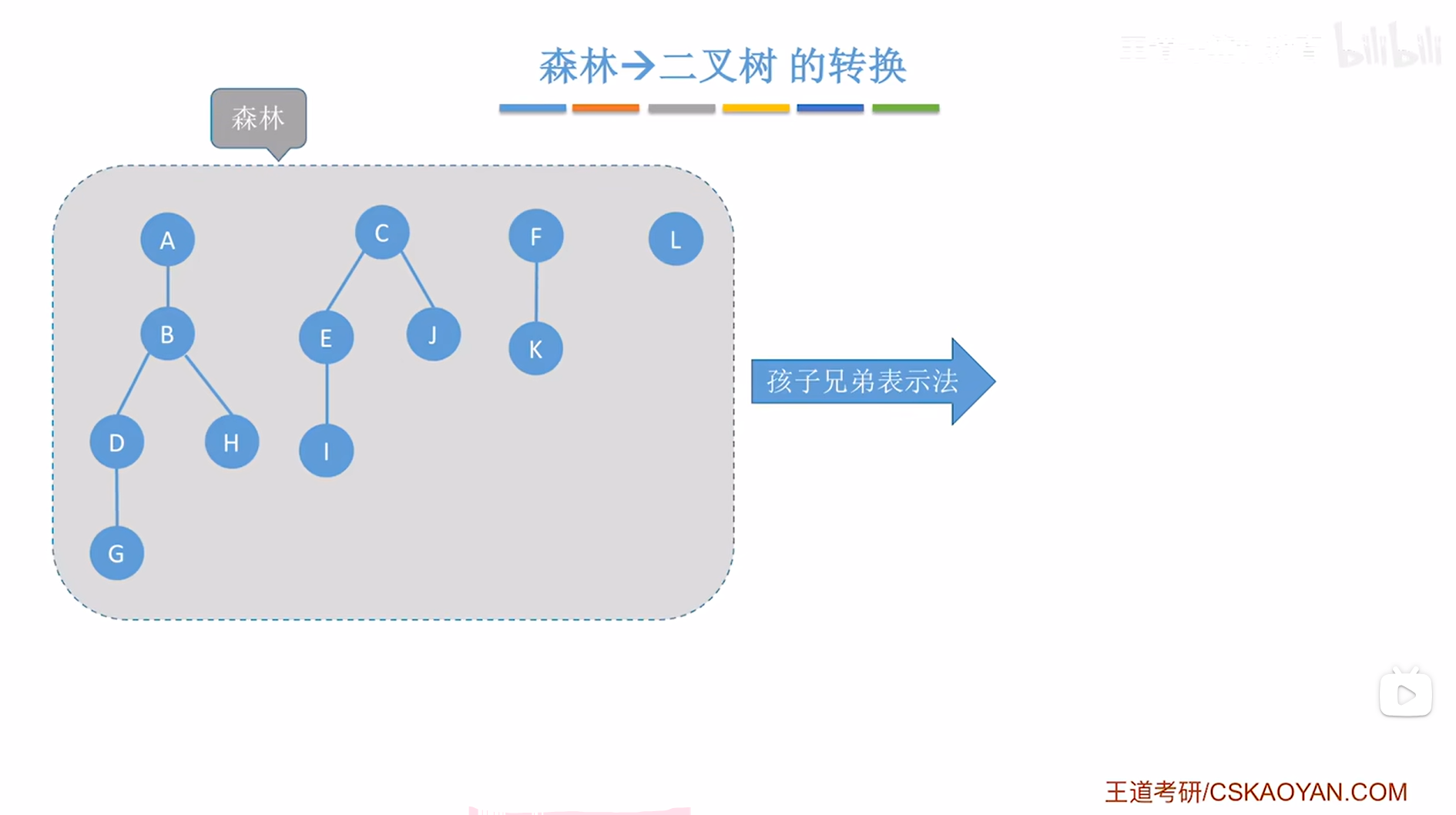
如上图,
"森林->二叉树"的转换思路与"树->二叉树"的转换思路类似,
唯一需要注意的是第一步中树只有1个根结点,而森林至少有2两个平级的根结点,
森林中所有的根结点视为平级的兄弟结点,
所以森林转换为二叉树的时候,第一步需要把森林中所有的根结点用右指针"串成糖葫芦",
本例中森林的根结点为A、C、F、L,
如下图:
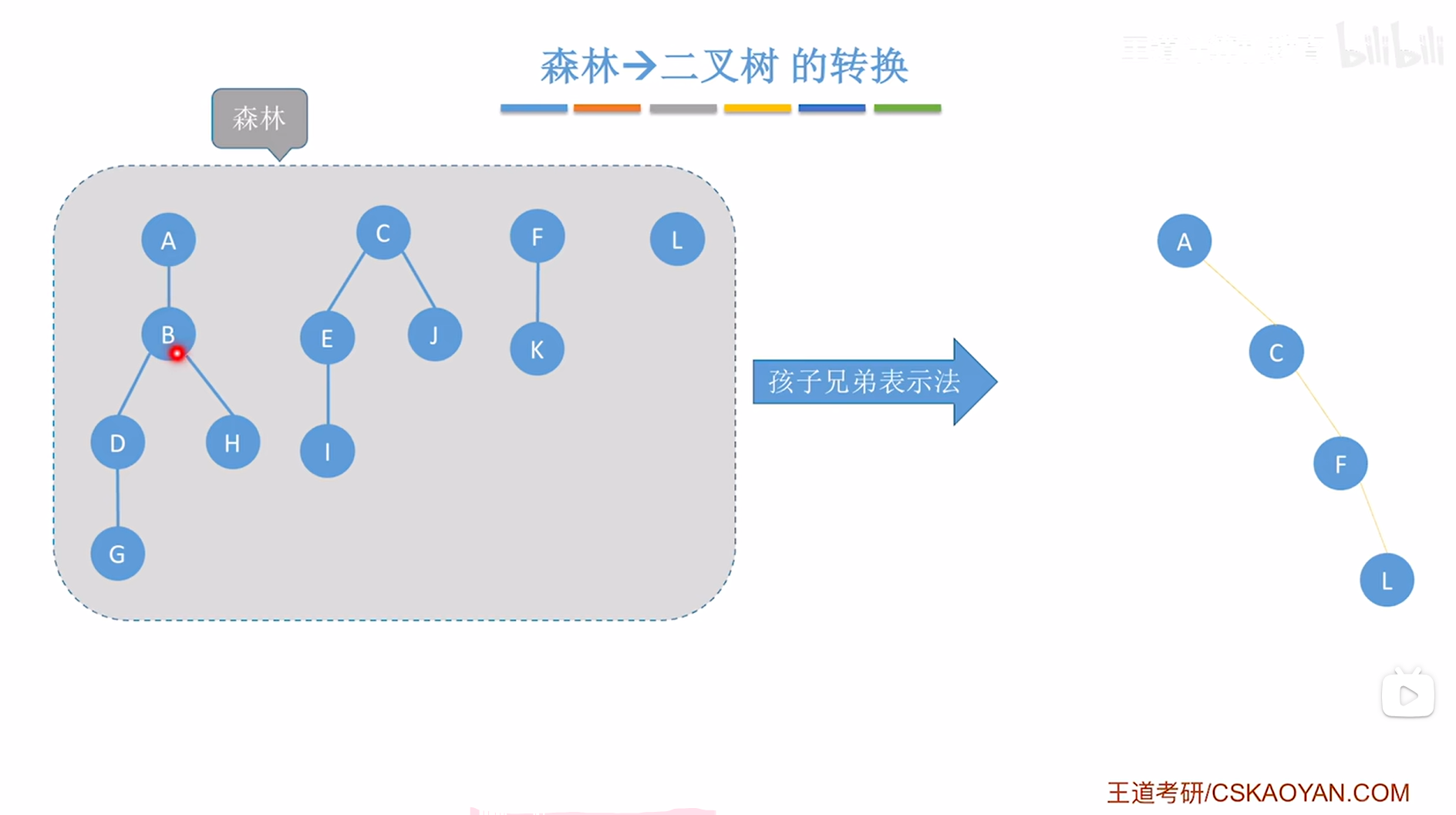
如上图,
接下来按照"森林的层序"依次处理每个结点,"森林的层序"就是指把整个森林看作一个整体,
第一层就是A、C、F、L,第二层就是B、E、J、K,第三层就是D、H、I,第四层就是G,因此处理顺序就是A->C->F->L->B->E->J->K->D->H->I->G,
处理方法同例一,
最终的结果如下图:
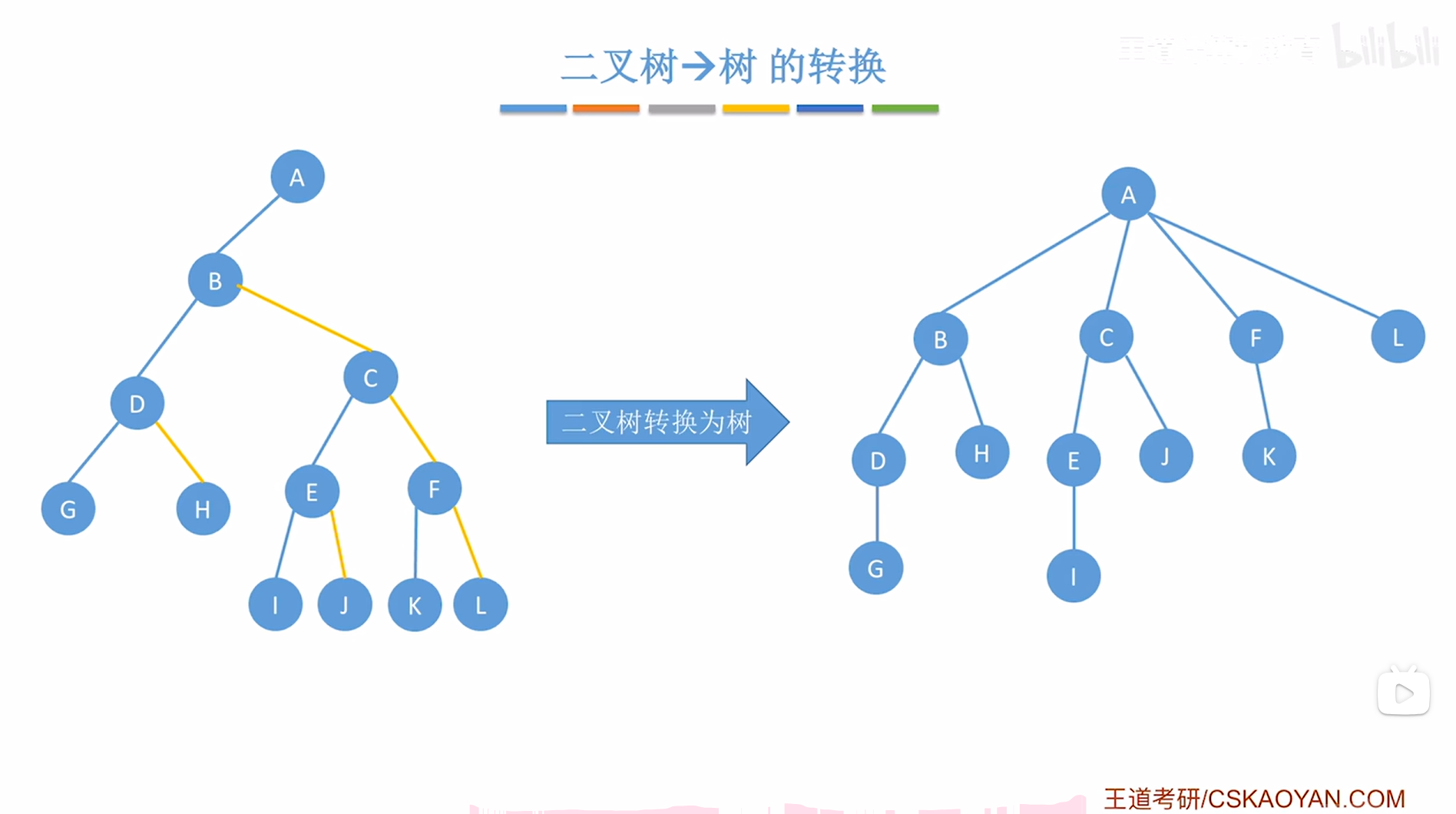
三."二叉树->树"的转换:
1.例一:
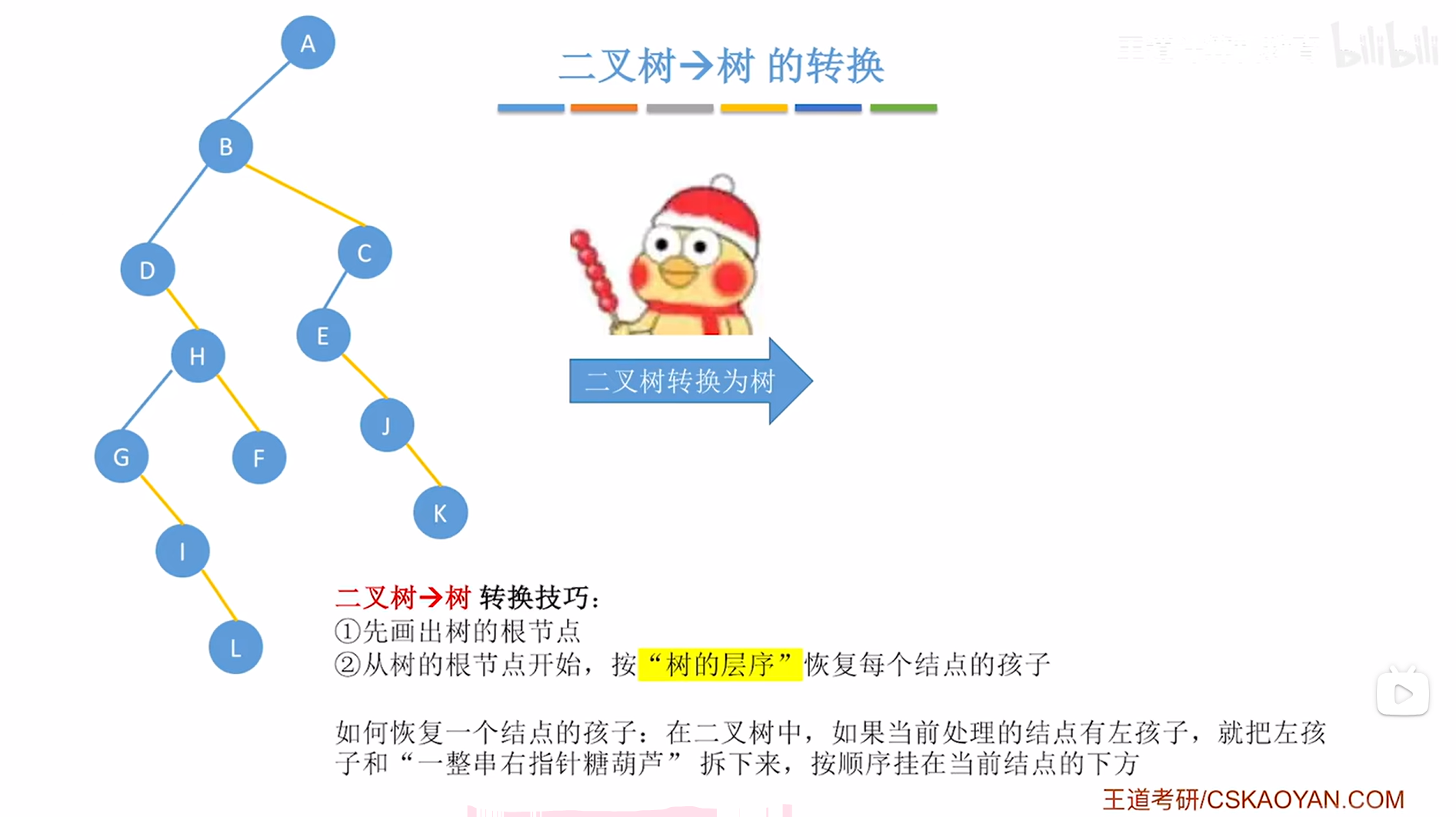
以上述图片左边的二叉树为例,
现在把该二叉树转换为树,
"二叉树->树"的转换技巧:
- 先画出树的根结点
- 从树的根结点开始,按"树的层序"恢复每个结点的孩子
(注:按"树的层序"是为了不容易出错)
上述图片左边的二叉树的根结点为A,因此转换后的树的根结点为A,
如下图:
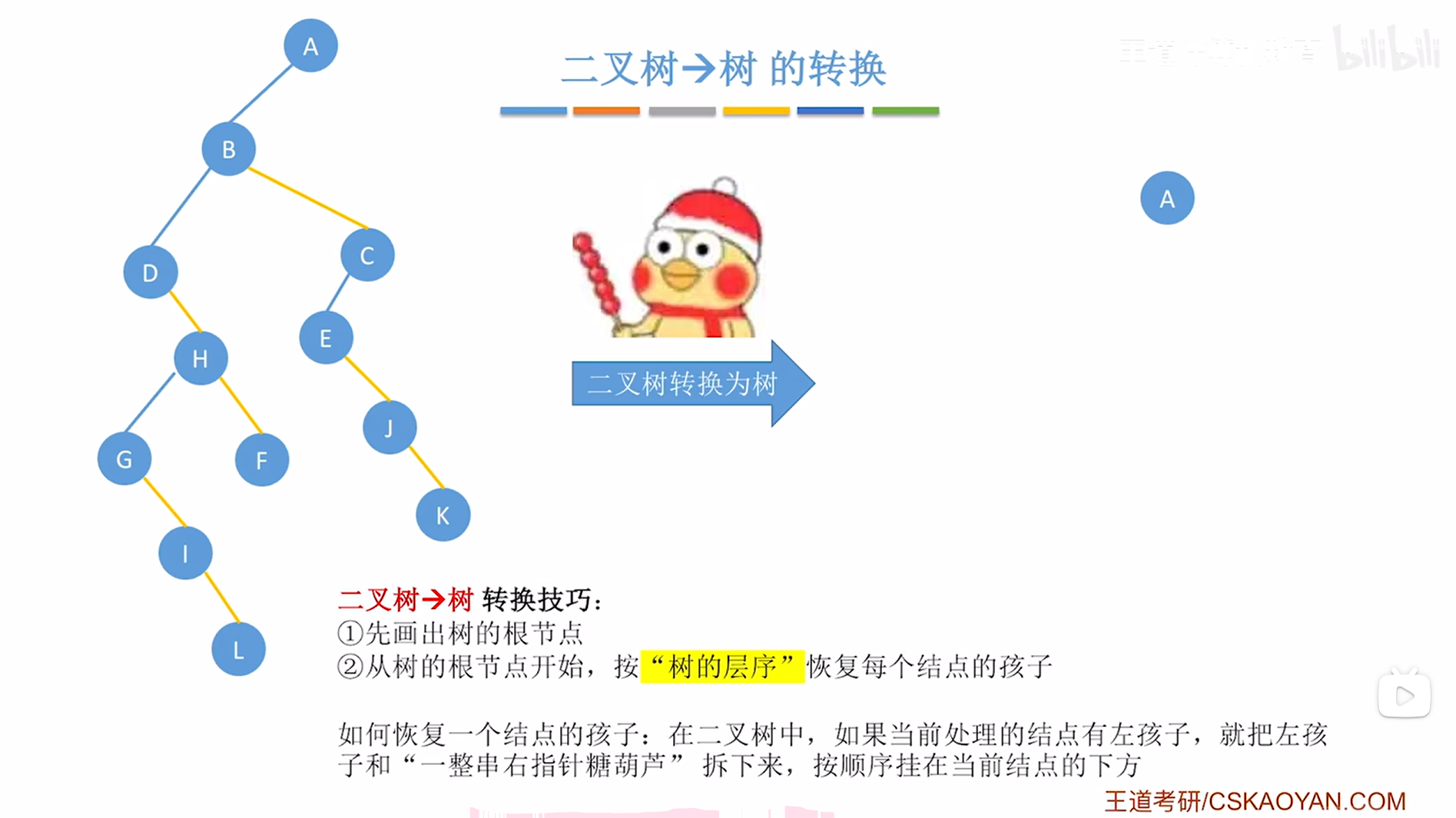
如上图,
接下来从树的根结点A开始,按"树的层序"恢复每个结点的孩子(注意是从树的层序开始恢复,不是二叉树,也就是按照上述图片右边的树的层序恢复,不是上述图片左边的二叉树),
那么如何恢复一个结点的孩子呢?
当前处理的是根结点A,也就是要恢复结点A的孩子,此时就要观察在上述图片内左侧的二叉树中结点A有没有左孩子,如果有左孩子,那么就要把它的左孩子以及"一整串右指针糖葫芦"拆下来(如果没有左孩子,就不需要做恢复孩子的处理;如果有左孩子但没有"一整串右指针糖葫芦",那么只需要把左孩子挂上即可,"一整串右指针糖葫芦"看作NULL)->对于A结点来说,就需要把它的左孩子即B结点以及"一整串右指针糖葫芦"即C结点拆下来,再把B、C分别挂在A结点的下方,
如下图:
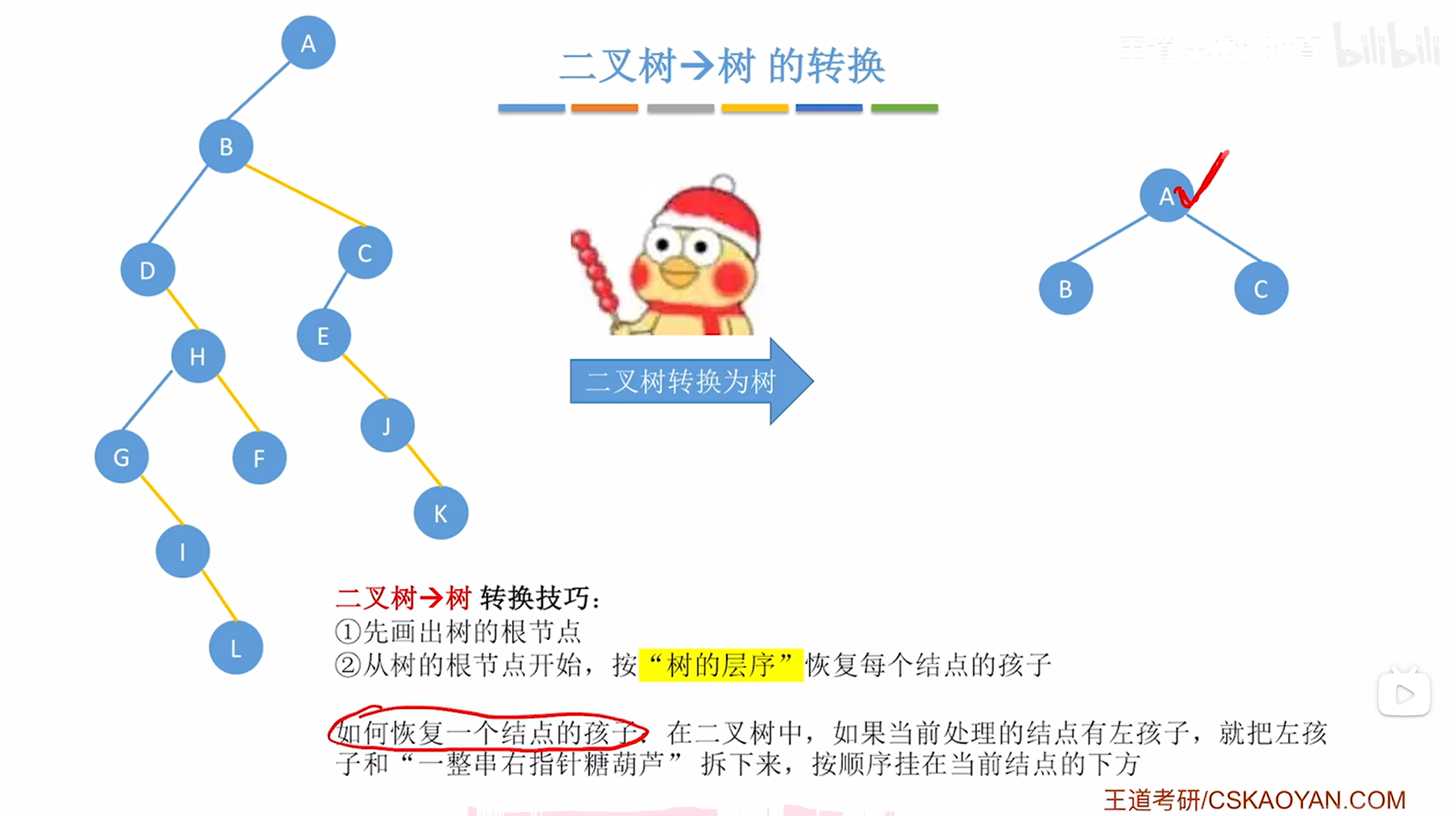
如上图,
至此,A结点的孩子恢复完毕,按照"树的层序",接下来要恢复B结点的孩子(注:是按照树的层序,即按照上述图片右边的树的层序,不是上述图片左边的二叉树),
当前处理的是B结点,此时就要观察在上述图片内左侧的二叉树中结点B有没有左孩子,如果有左孩子,那么就要把它的左孩子以及"一整串右指针糖葫芦"拆下来->对于B结点来说,就需要把它的左孩子即D结点以及"一整串右指针糖葫芦"即H、F结点拆下来,再把D、H、F分别挂在B结点的下方,
如下图:
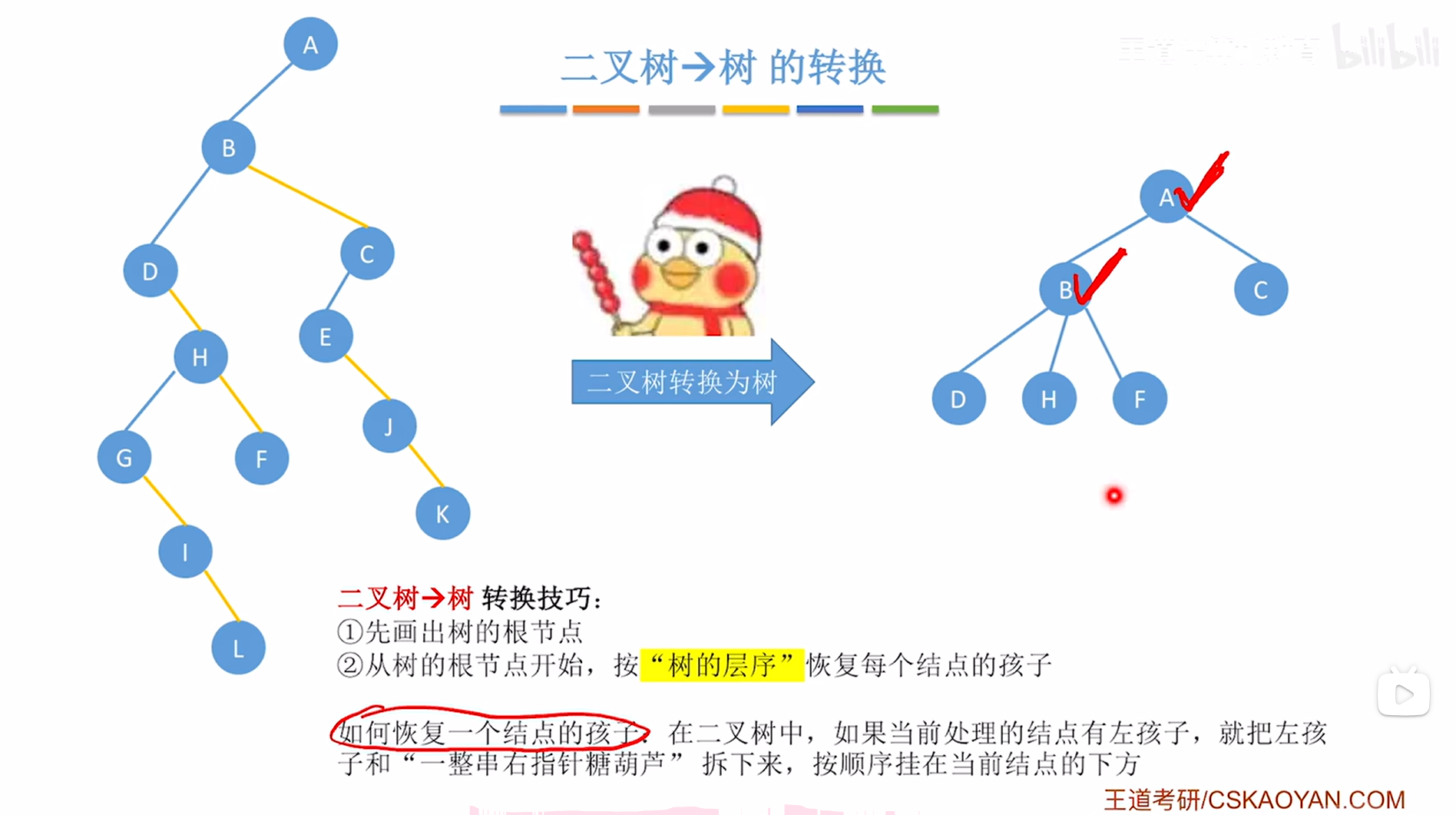
如上图,
至此,B结点的孩子恢复完毕,按照"树的层序",接下来要恢复C结点的孩子(注:是按照树的层序,即按照上述图片右边的树的层序,不是上述图片左边的二叉树),
当前处理的是C结点,此时就要观察在上述图片内左侧的二叉树中结点C有没有左孩子,如果有左孩子,那么就要把它的左孩子以及"一整串右指针糖葫芦"拆下来->对于C结点来说,就需要把它的左孩子即E结点以及"一整串右指针糖葫芦"即J、K结点拆下来,再把E、J、K分别挂在C结点的下方,
如下图:
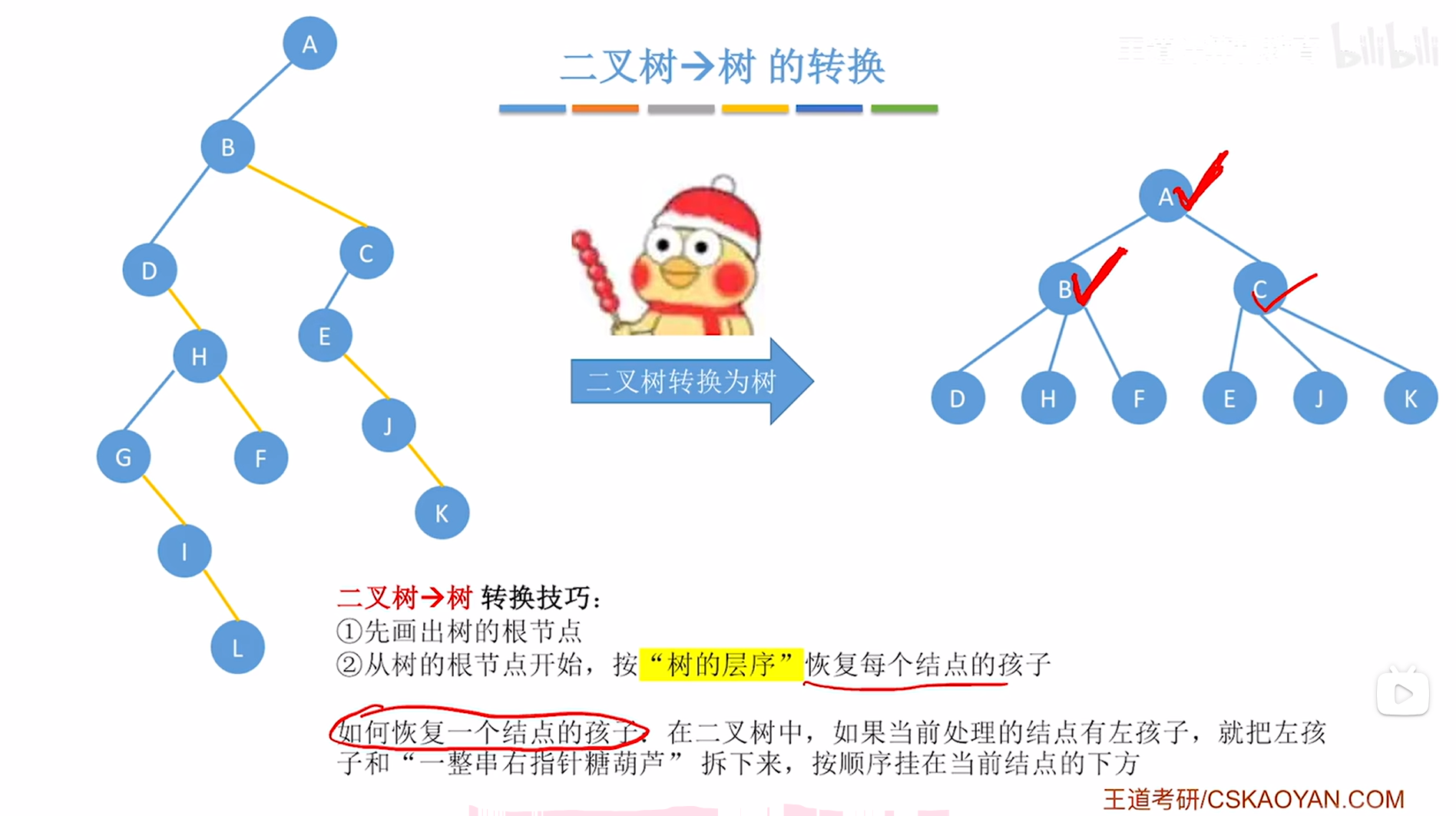
如上图,
至此,C结点的孩子恢复完毕,按照"树的层序",接下来要恢复D结点的孩子(注:是按照树的层序,即按照上述图片右边的树的层序,不是上述图片左边的二叉树),
当前处理的是D结点,此时就要观察在上述图片内左侧的二叉树中结点D有没有左孩子,如果有左孩子,那么就要把它的左孩子以及"一整串右指针糖葫芦"拆下来->对于D结点来说,由于D结点的左指针为空,说明D结点没有左孩子,所以D结点不需要做恢复孩子的处理;
至此,D结点的孩子恢复完毕,按照"树的层序",接下来要恢复H结点的孩子(注:是按照树的层序,即按照上述图片右边的树的层序,不是上述图片左边的二叉树),
当前处理的是H结点,此时就要观察在上述图片内左侧的二叉树中结点H有没有左孩子,如果有左孩子,那么就要把它的左孩子以及"一整串右指针糖葫芦"拆下来->对于H结点来说,就需要把它的左孩子即G结点以及"一整串右指针糖葫芦"即I、L结点拆下来,再把G、I、L分别挂在H结点的下方,
如下图:
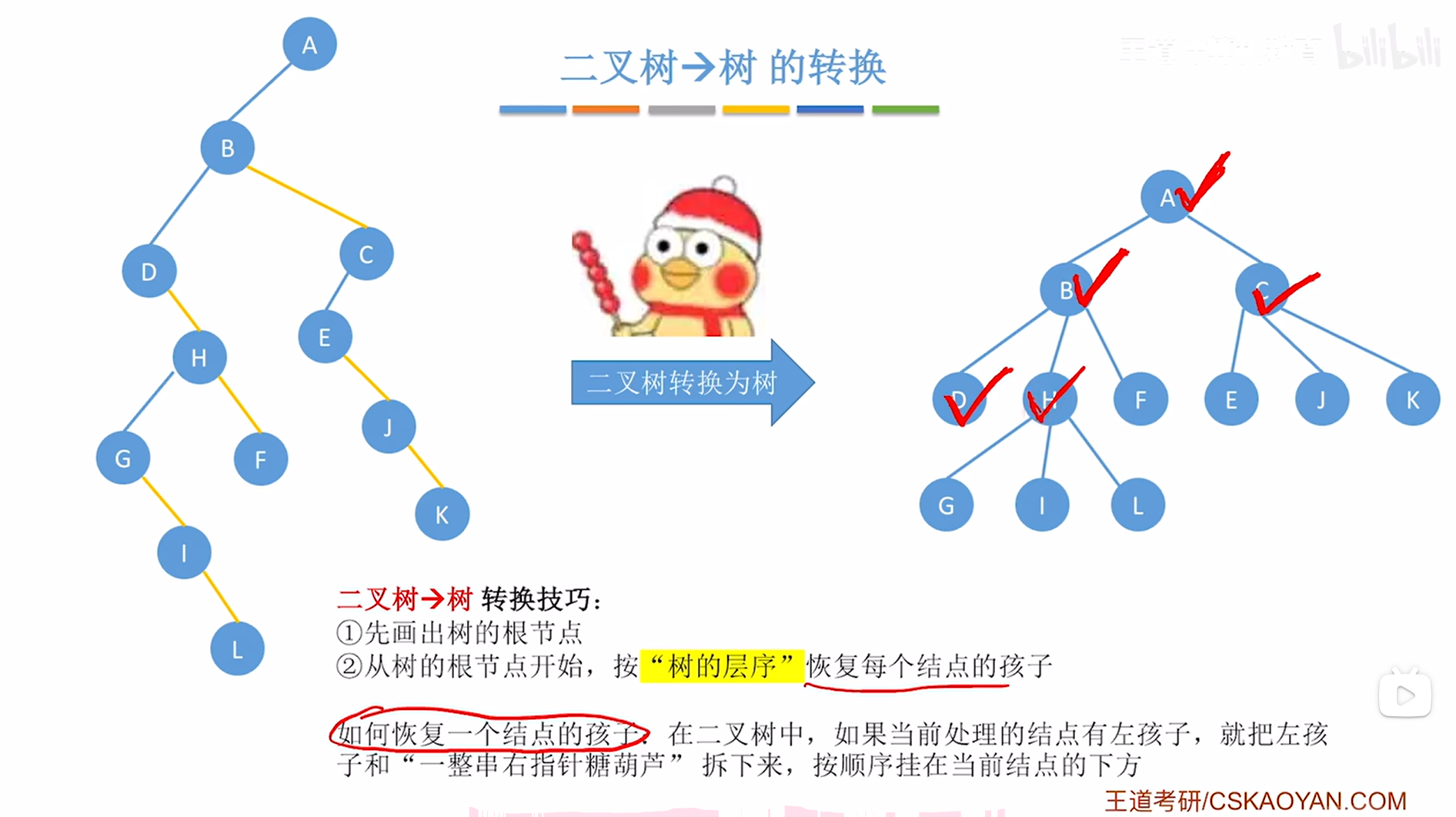
如上图,
至此,H结点的孩子恢复完毕,按照"树的层序",接下来要依次恢复F、E、J、K、G、I、L结点的孩子(注:是按照树的层序,即按照上述图片右边的树的层序,不是上述图片左边的二叉树),
然而对于F、E、J、K、G、I、L结点来说,F、E、J、K、G、I、L结点在上述图片内左侧的二叉树中都没有左孩子,所以F、E、J、K、G、I、L结点都不需要做恢复孩子的处理,
至此,就完成了上述图片中左边的"二叉树->树"的转换,
如下图:
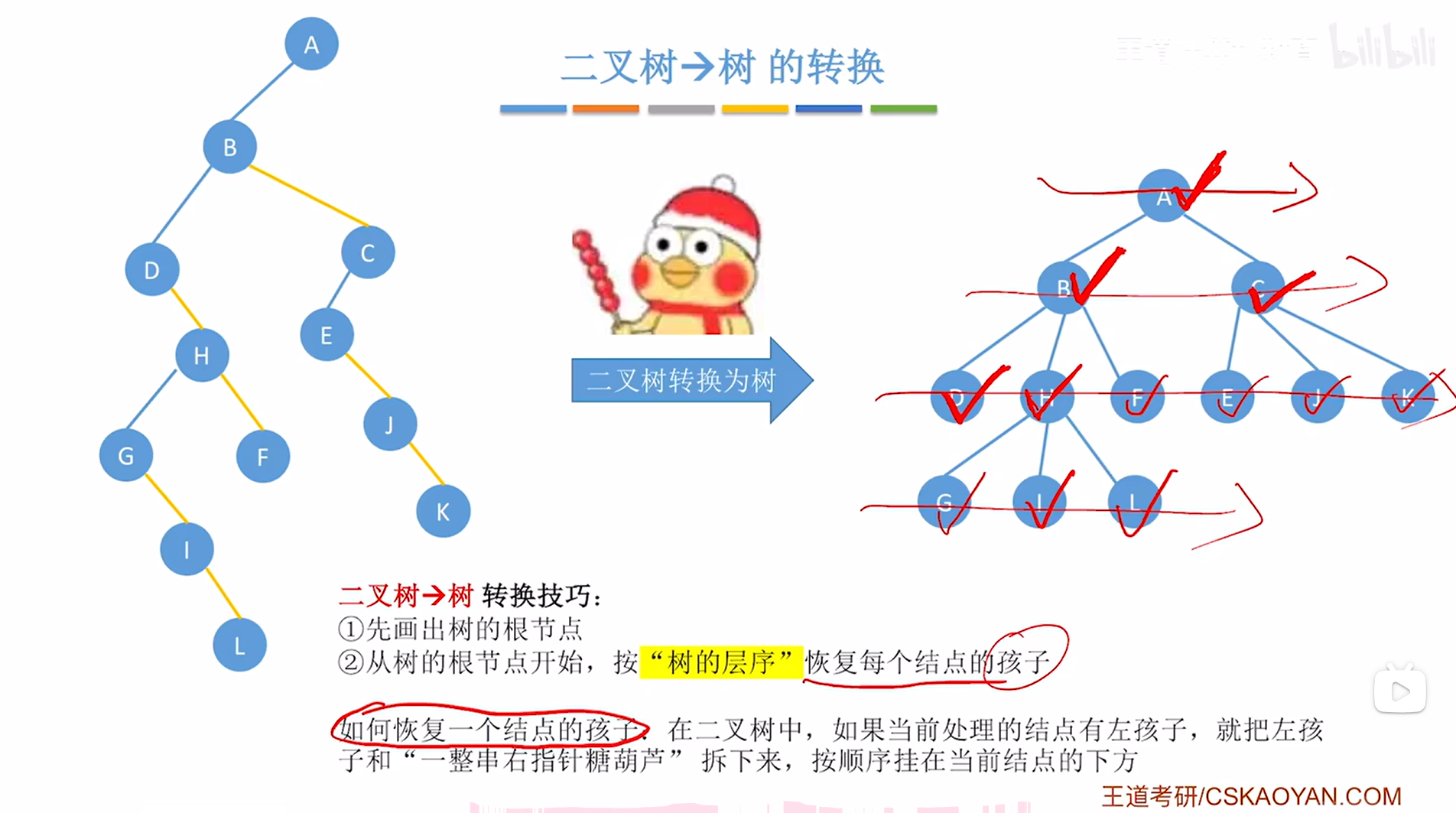
2.例二:原理同例一
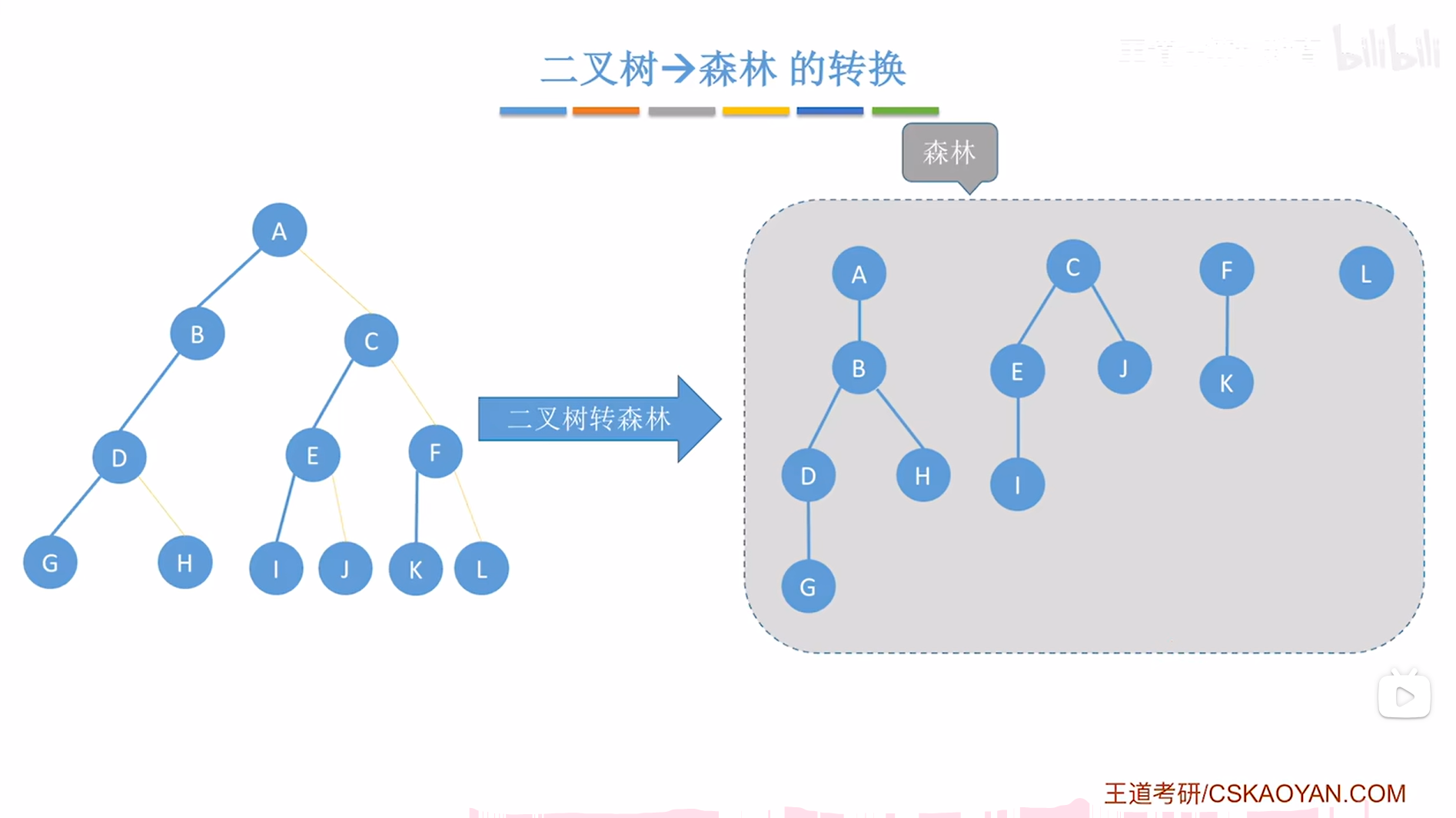
四."二叉树->森林"的转换:
1.例一:
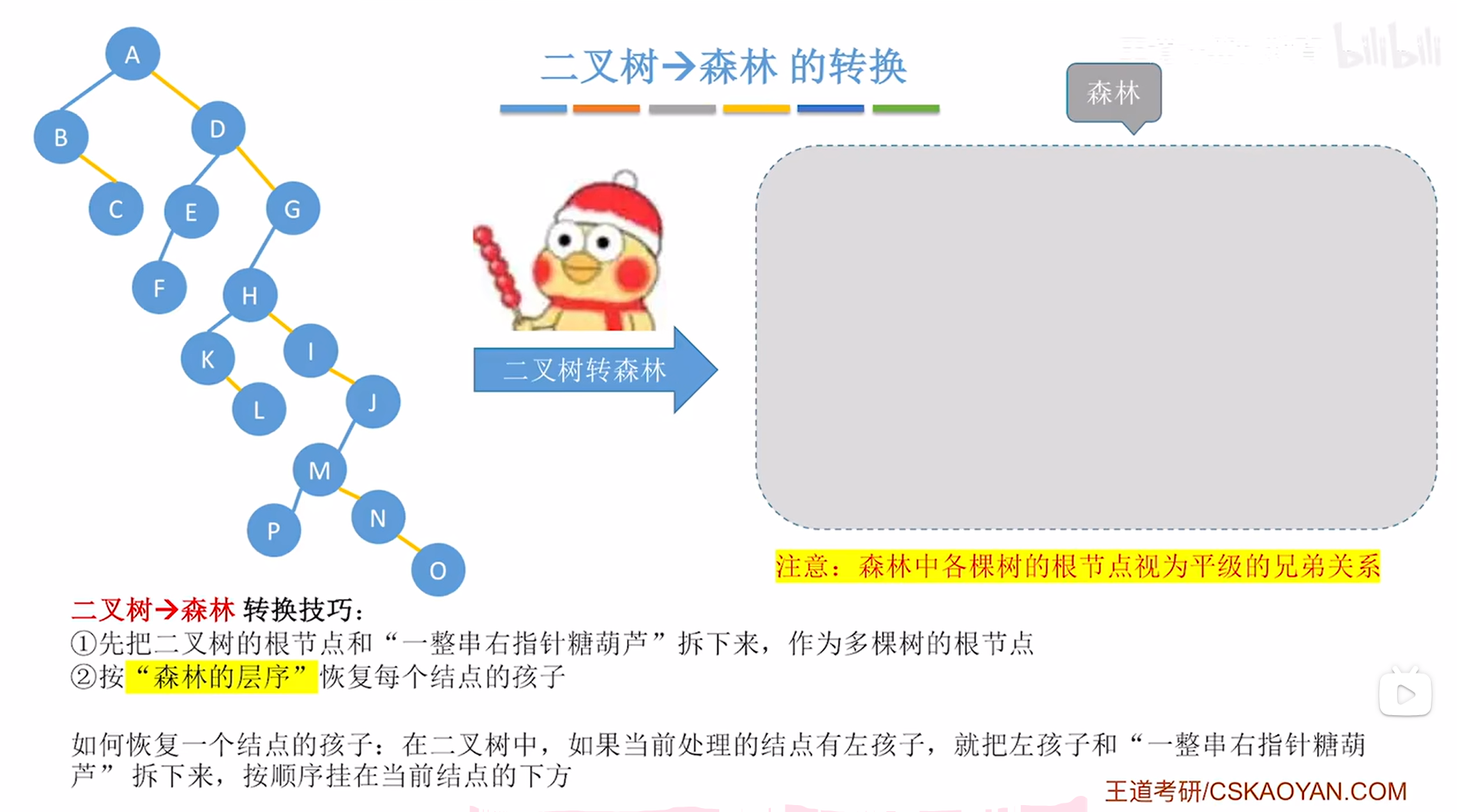
如上图,
"二叉树->森林"的转换思路与"二叉树->树"的转换思路类似,
唯一需要注意的是森林中至少有两棵树,
所以把二叉树转换为森林的时候首先要把二叉树的根结点和根结点右指针上的一整串结点全部拆下来,
上述图片中左边的二叉树的根结点为A,A的右指针上的一整串结点依次为D、G,
因此A、D、G分别是该森林中三棵树的根结点,
如下图:
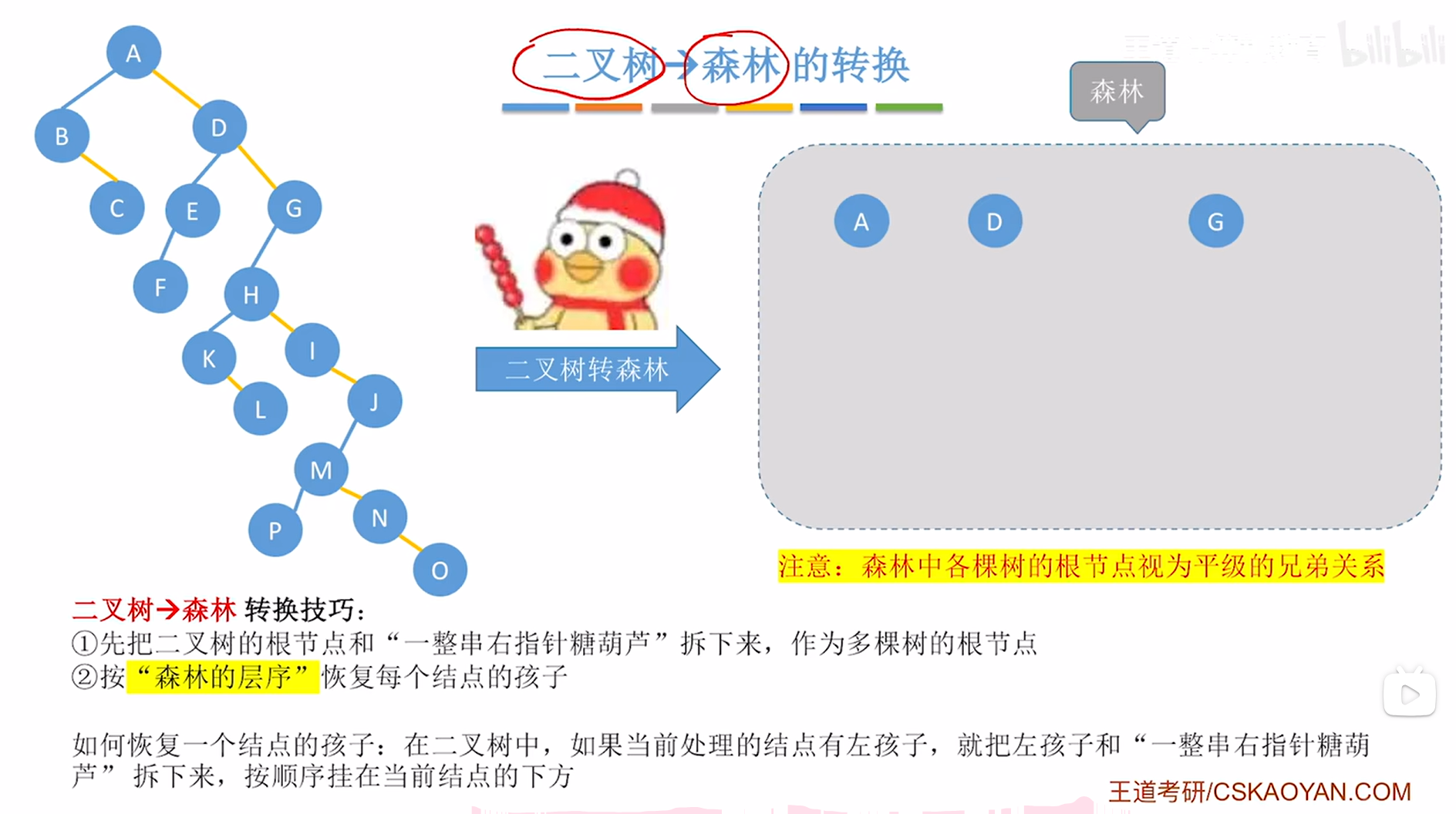
如上图,
接下来按照"森林的层序"依次恢复结点的孩子,
首先需要恢复A结点的孩子,此时就要观察在上述图片内左侧的二叉树中结点A有没有左孩子,如果有左孩子,那么就要把它的左孩子以及"一整串右指针糖葫芦"拆下来->对于A结点来说,就需要把它的左孩子即B结点以及"一整串右指针糖葫芦"即C结点拆下来,再把B、C分别挂在A结点的下方,
如下图:
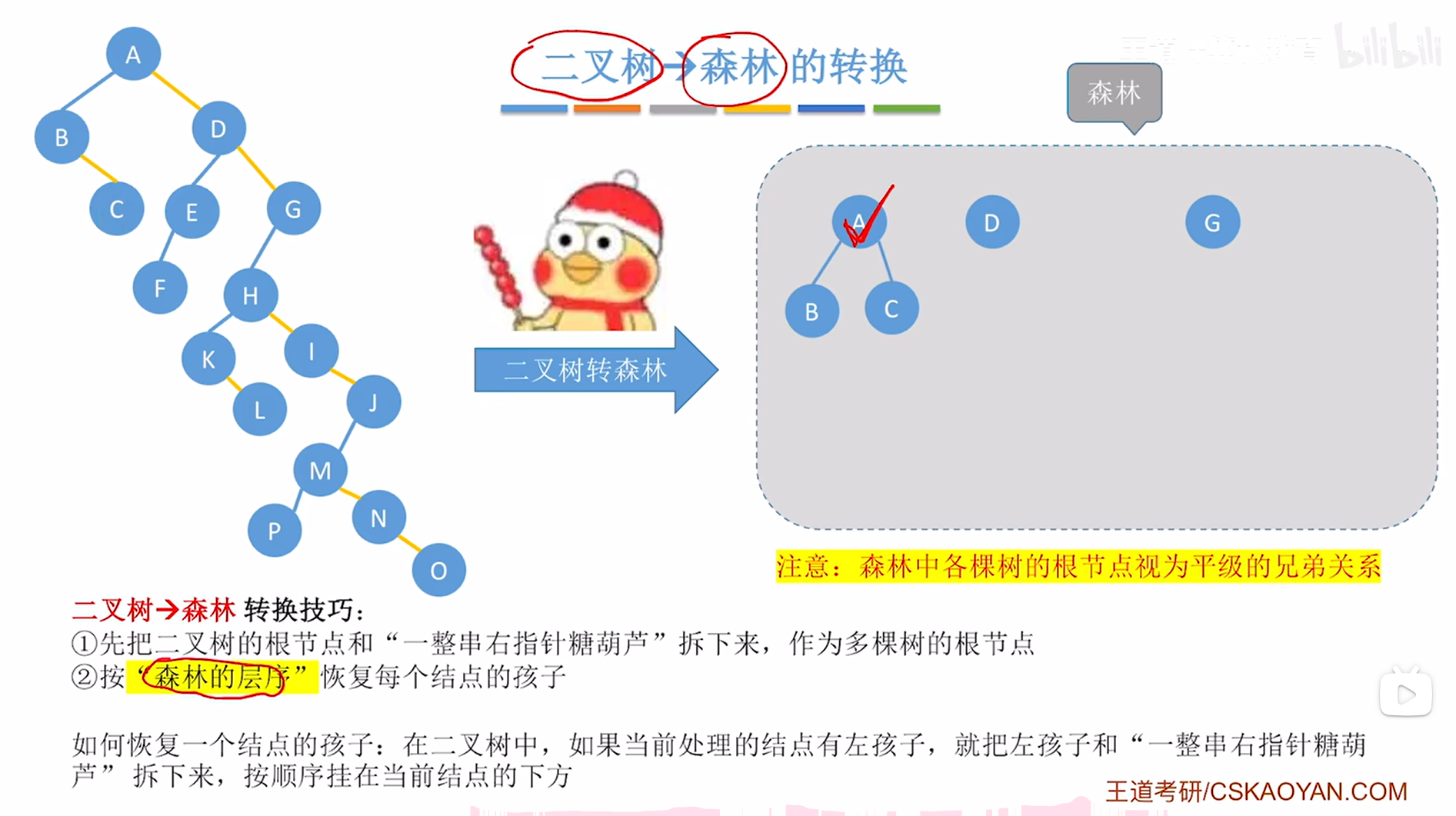
如上图,
至此,A结点的孩子恢复完毕,接下来按照"森林的层序"依次恢复结点的孩子,
因此需要恢复D结点的孩子,此时就要观察在上述图片内左侧的二叉树中结点D有没有左孩子,如果有左孩子,那么就要把它的左孩子以及"一整串右指针糖葫芦"拆下来->对于D结点来说,就需要把它的左孩子即E结点拆下来,由于E结点的"一整串右指针糖葫芦"为空,因此不需要管,所以只需要把E挂在D结点的下方即可,
如下图:
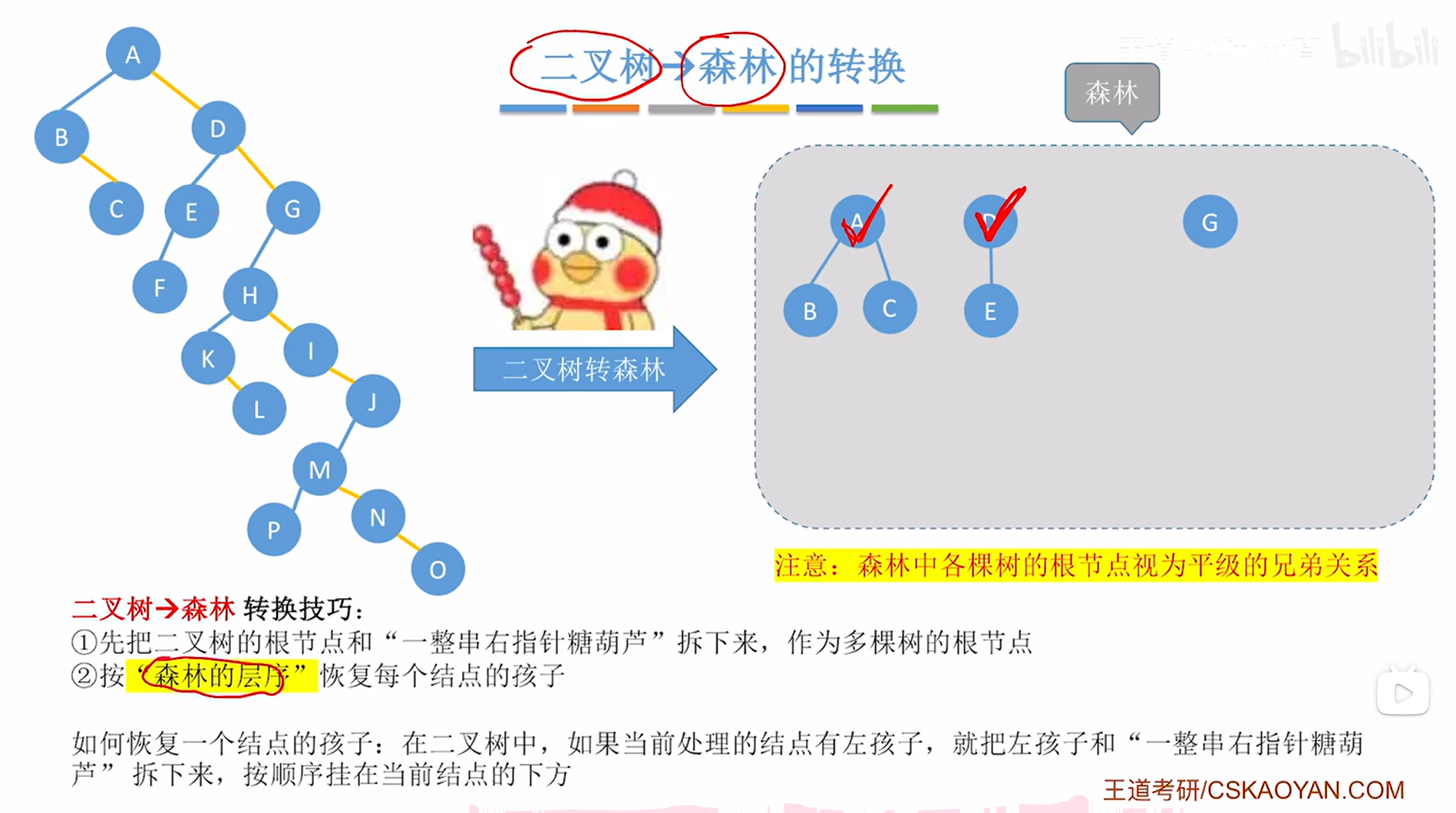
如上图,
至此,D结点的孩子恢复完毕,接下来按照"森林的层序"依次恢复结点的孩子,
因此需要恢复G结点的孩子,此时就要观察在上述图片内左侧的二叉树中结点G有没有左孩子,如果有左孩子,那么就要把它的左孩子以及"一整串右指针糖葫芦"拆下来->对于G结点来说,就需要把它的左孩子即H结点以及"一整串右指针糖葫芦"即I、J结点拆下来,再把H、I、J分别挂在G结点的下方,
如下图:
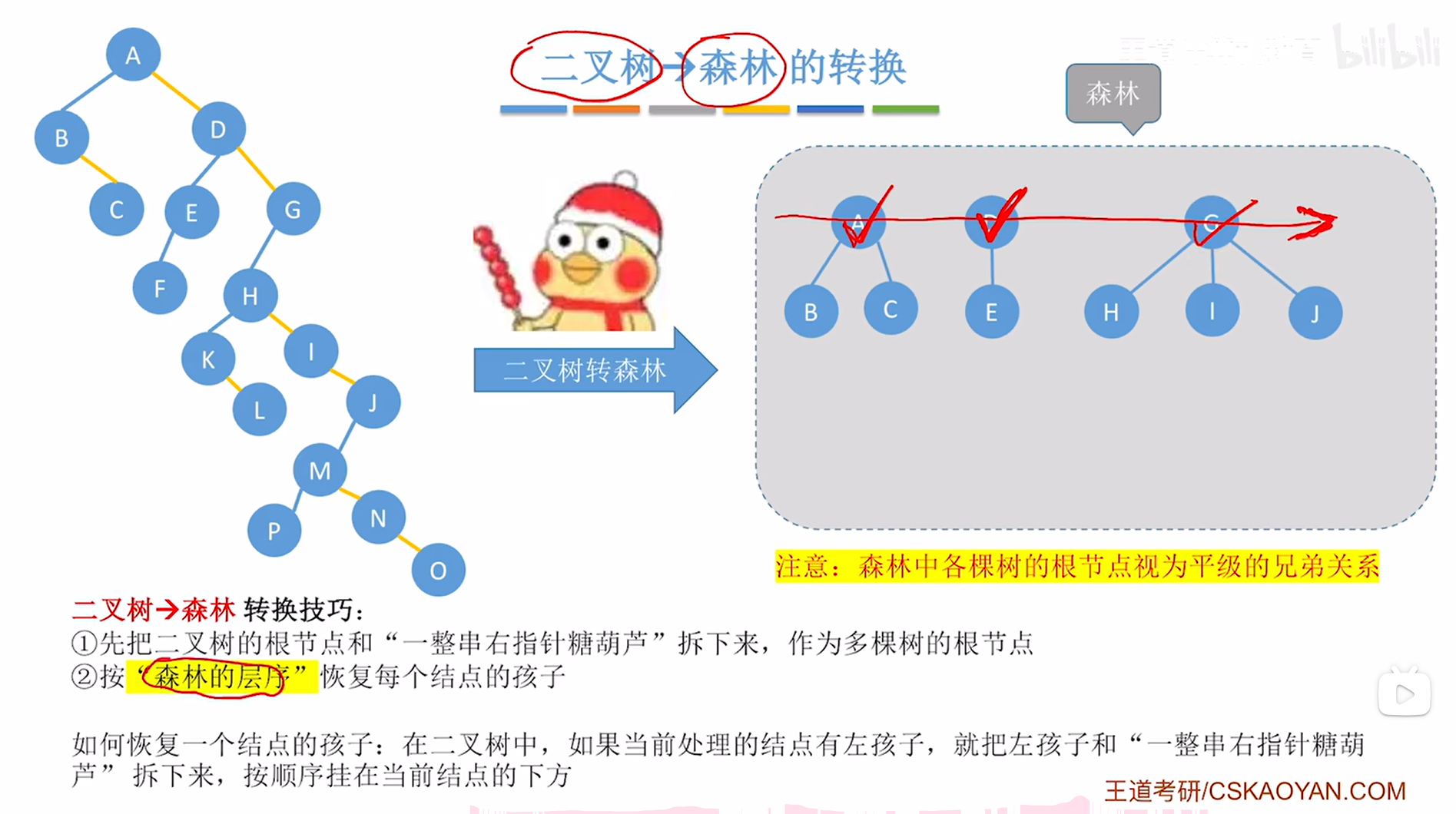
如上图,
至此,G结点的孩子恢复完毕,接下来按照"森林的层序"依次恢复结点的孩子,
因此需要恢复B结点的孩子,此时就要观察在上述图片内左侧的二叉树中结点B有没有左孩子,如果有左孩子,那么就要把它的左孩子以及"一整串右指针糖葫芦"拆下来->对于B结点来说,B结点没有左孩子,因此B结点不需要做恢复孩子的处理,同理按照"森林的层序"接下来需要恢复C结点的孩子,由于C结点在上述图片内左侧的二叉树中没有左孩子,所以也不需要做恢复孩子的处理;
接下来按照"森林的层序"依次恢复结点的孩子,
因此需要恢复E结点的孩子,此时就要观察在上述图片内左侧的二叉树中结点E有没有左孩子,如果有左孩子,那么就要把它的左孩子以及"一整串右指针糖葫芦"拆下来->对于E结点来说,就需要把它的左孩子即F结点拆下来,由于F结点的"一整串右指针糖葫芦"为空,因此不需要管,所以只需要把F挂在E结点的下方即可,
如下图:
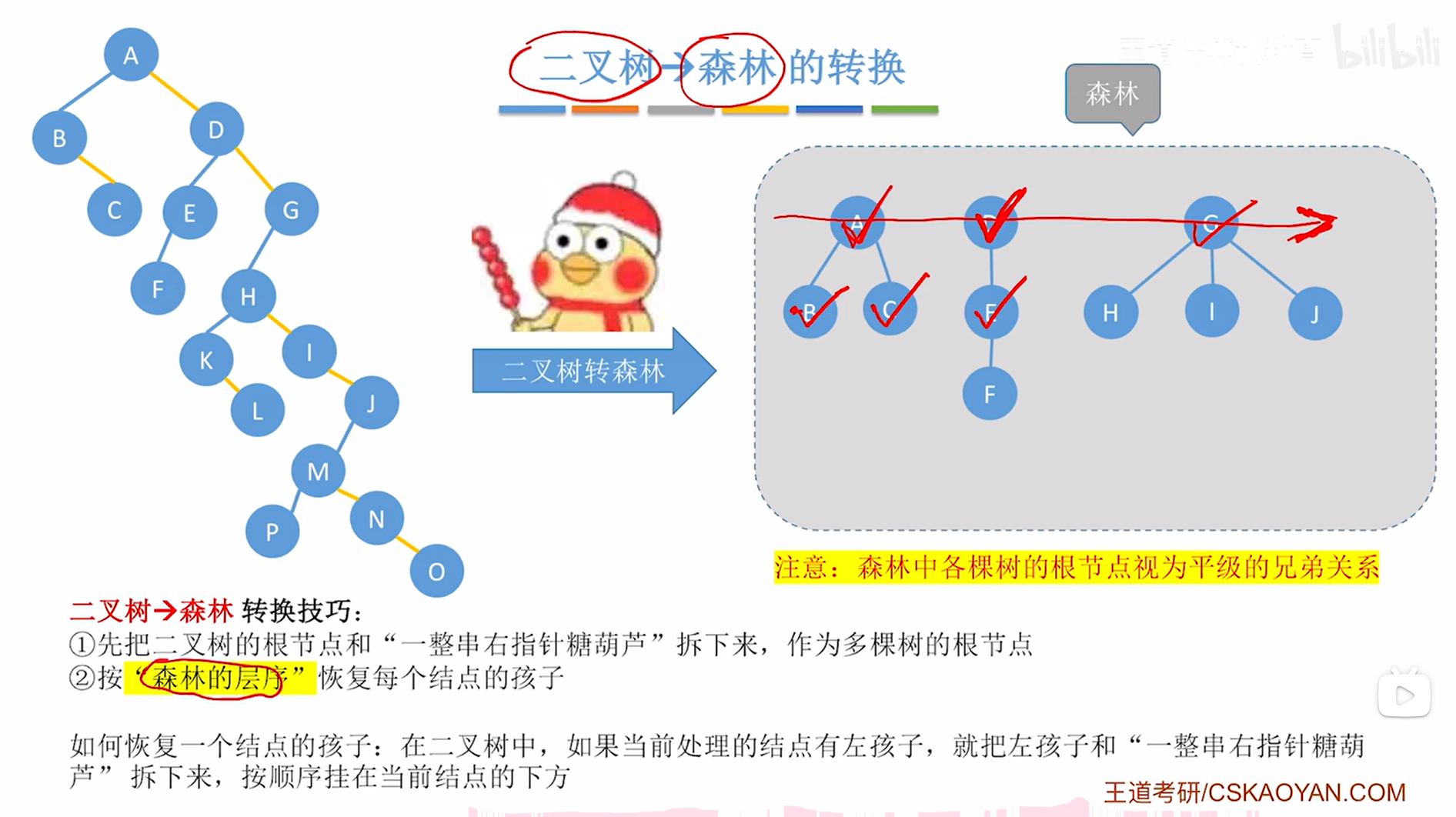
如上图,
至此,E结点的孩子恢复完毕,接下来按照"森林的层序"依次恢复结点的孩子,
因此需要恢复H结点的孩子,此时就要观察在上述图片内左侧的二叉树中结点H有没有左孩子,如果有左孩子,那么就要把它的左孩子以及"一整串右指针糖葫芦"拆下来->对于H结点来说,就需要把它的左孩子即K结点以及"一整串右指针糖葫芦"即L结点拆下来,再把K、L分别挂在H结点的下方,
如下图:
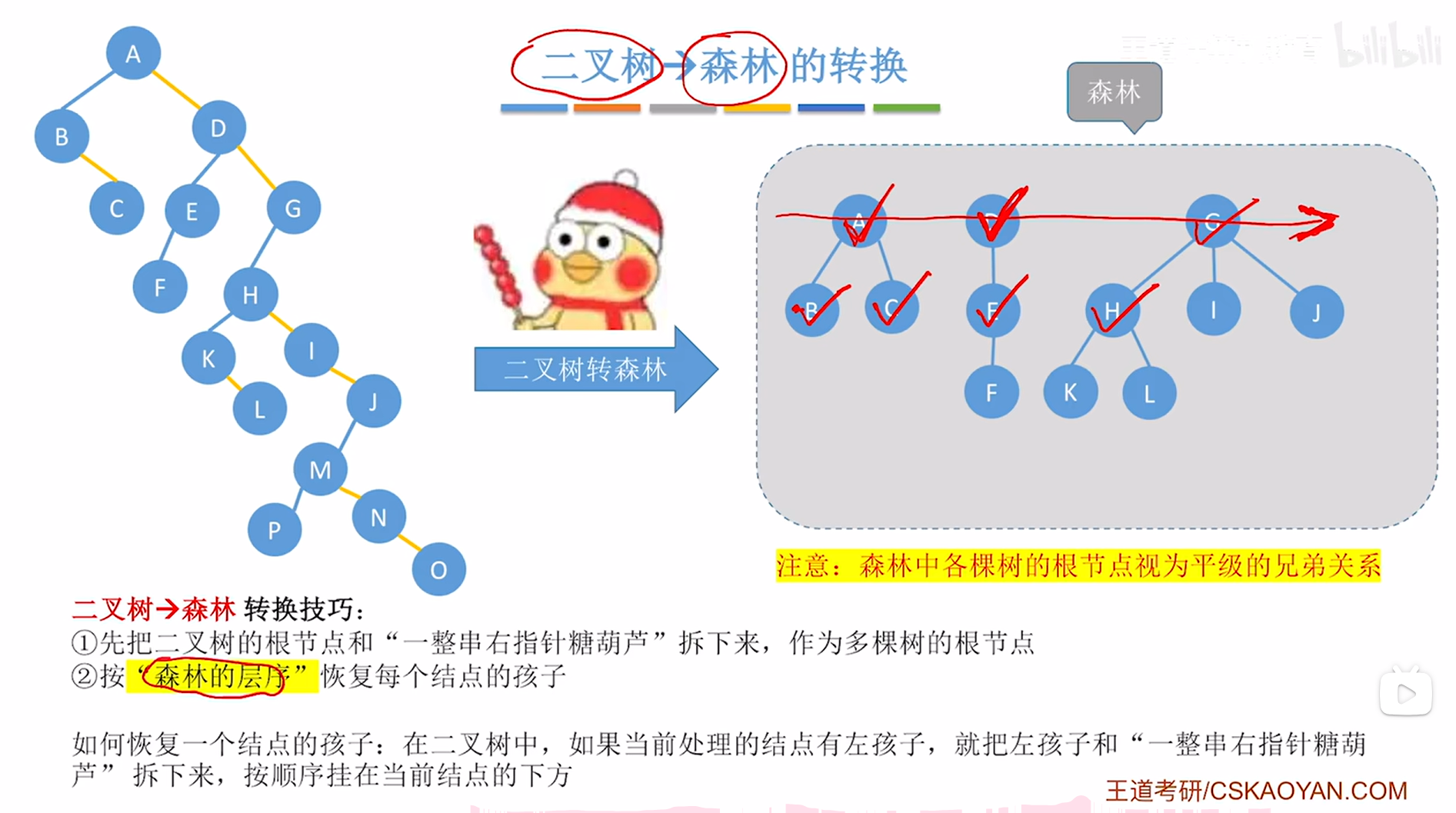
如上图,
至此,H结点的孩子恢复完毕,接下来按照"森林的层序"依次恢复结点的孩子,
因此需要恢复I结点的孩子,此时就要观察在上述图片内左侧的二叉树中结点I有没有左孩子,如果有左孩子,那么就要把它的左孩子以及"一整串右指针糖葫芦"拆下来->对于I结点来说,I结点没有左孩子,因此I结点不需要做恢复孩子的处理;
接下来按照"森林的层序"依次恢复结点的孩子,
因此需要恢复J结点的孩子,此时就要观察在上述图片内左侧的二叉树中结点J有没有左孩子,如果有左孩子,那么就要把它的左孩子以及"一整串右指针糖葫芦"拆下来->对于J结点来说,就需要把它的左孩子即M结点以及"一整串右指针糖葫芦"即N、O结点拆下来,再把M、N、O分别挂在J结点的下方,
如下图:
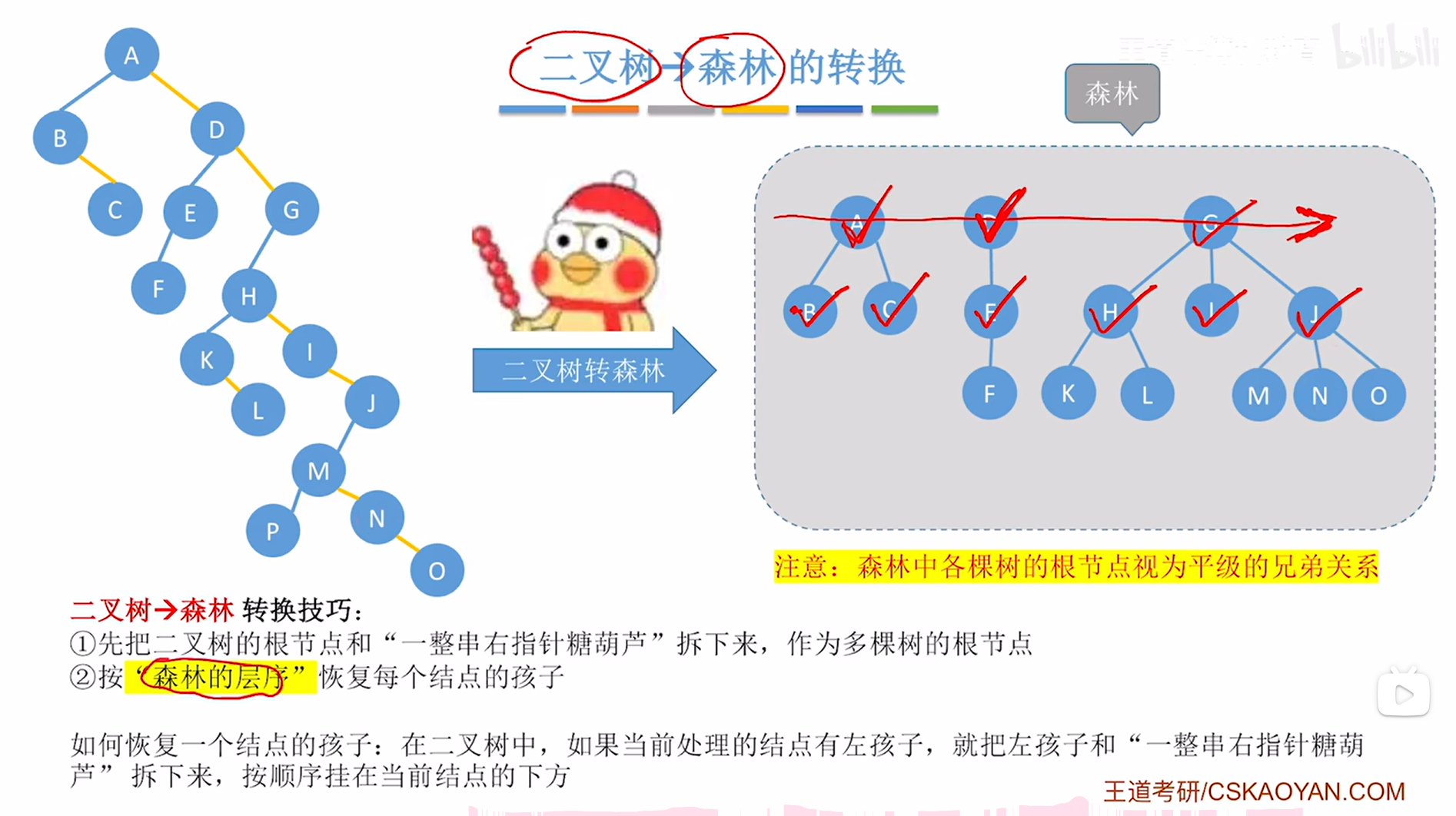
如上图,
至此,J结点的孩子恢复完毕,接下来按照"森林的层序"依次恢复结点的孩子,
因此需要依次恢复F、K、L结点的孩子,此时就要观察在上述图片内左侧的二叉树中结点F、K、L有没有左孩子,如果有左孩子,那么就要把它们的左孩子以及"一整串右指针糖葫芦"拆下来->对于F、K、L结点来说,F、K、L结点都没有左孩子,因此F、K、L结点都不需要做恢复孩子的处理;
接下来按照"森林的层序"依次恢复结点的孩子,
因此需要恢复M结点的孩子,此时就要观察在上述图片内左侧的二叉树中结点M有没有左孩子,如果有左孩子,那么就要把它的左孩子以及"一整串右指针糖葫芦"拆下来->对于M结点来说,就需要把它的左孩子即P结点拆下来,由于P结点的"一整串右指针糖葫芦"为空,因此不需要管,所以只需要把P挂在M结点的下方即可,
如下图:
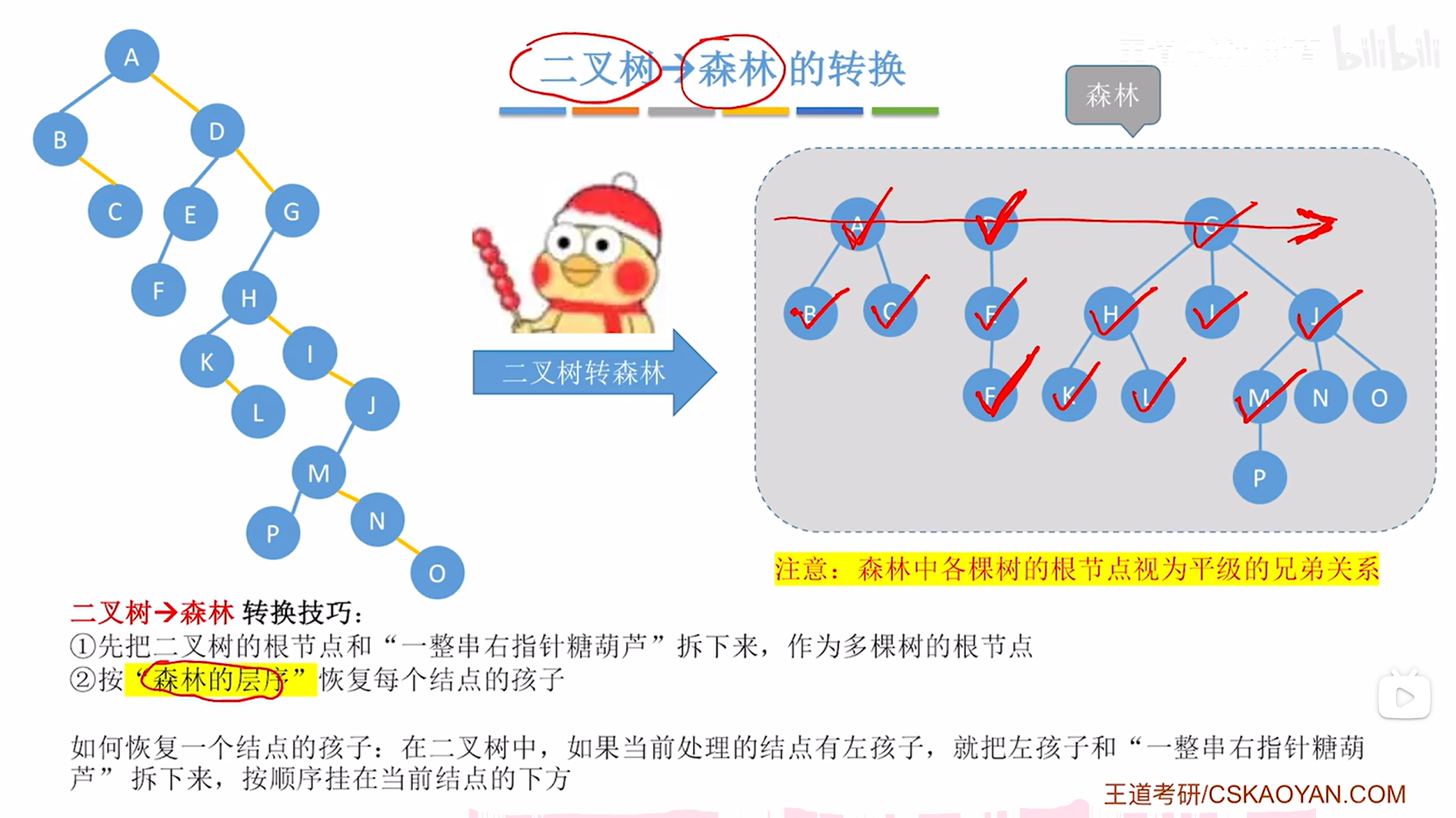
如上图,
至此,M结点的孩子恢复完毕,接下来按照"森林的层序"依次恢复结点的孩子,
因此需要依次恢复N、O、P结点的孩子,此时就要观察在上述图片内左侧的二叉树中结点N、O、P有没有左孩子,如果有左孩子,那么就要把它们的左孩子以及"一整串右指针糖葫芦"拆下来->对于N、O、P结点来说,N、O、P结点都没有左孩子,因此N、O、P结点都不需要做恢复孩子的处理,
至此,就完成了上述图片左边的"二叉树->森林"的转换,
如下图:
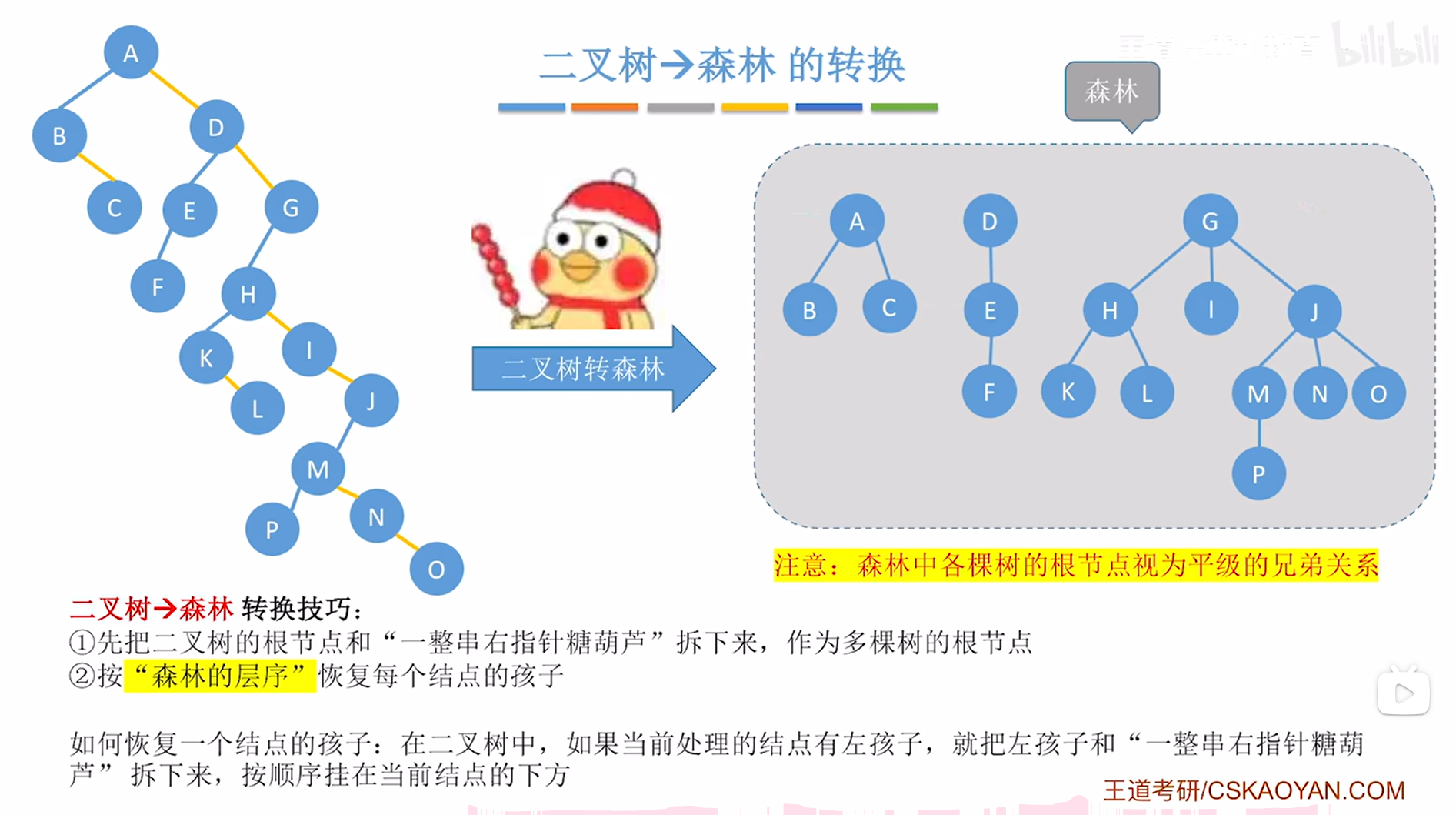
2.例二:原理同例一
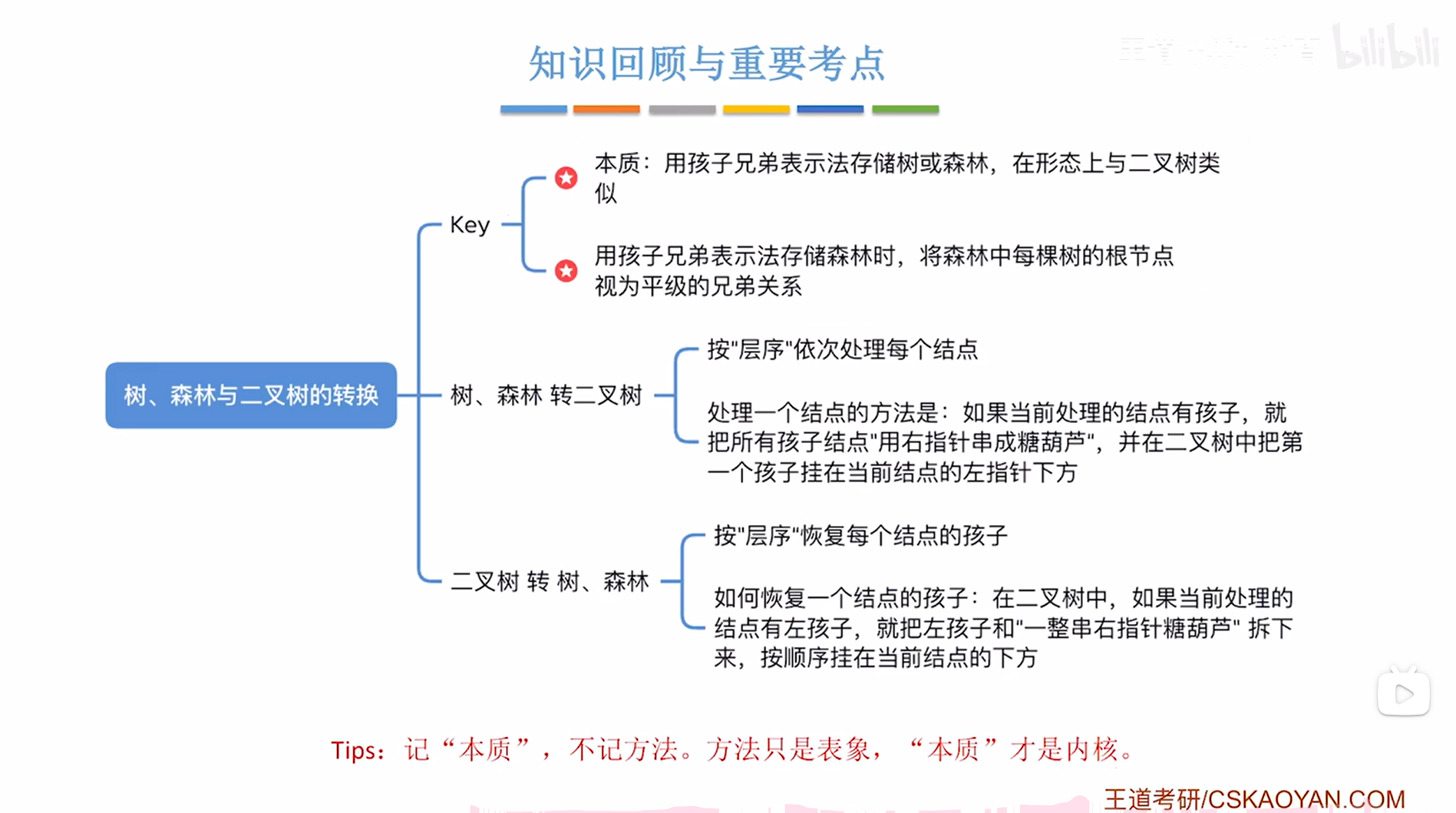
五.总结:









:Pandas 与数据库交互)
)
Ubuntu24.04下RTX5090配置IsaacSim与IsaacLab)
软件安装包下载及详细安装教程|附带安装文件)



的SVM多分类预测)

)
