随着对物理实相认识的深入，这个问题被一再提出，一再解决，但是从直觉上来说，始终没有达到一个令人满意的水平。问题是什么？既然一切皆是振动，那么这些振动是如何构造我们的物理实相的，比如如何构造了空间，如何构造了物质等等。

显然，首先得先定一个基本假设，也可以认为它不是一种假设，只是不得不这么说。这个基本假设就是，是我们自己的结构决定了我们的世界成为这个样子。至于什么决定了我们的结构，可以有很多解释，无论进化论还是神创论，还是各种能想到不能想到的，都没有差别。因为我们可以将这些可能的认识，都归结为本体自然发展的结果。也就是说，即便神创，仍然可以认为是本体发展过程的一种理解。基于这个基本假设，我们就可以把世界为什么是这个样子的，以人择原理来解释：因为我们是这样的。

但这仍然是哲学，不是可以应用到现实中的物理理论和方法。这里需要一个桥梁。这个桥梁可以帮助我们看懂，我们所看到的世界。

回来说物理，以及前置的数学。

在关于无限的讨论中，我们意识到，所谓无限，并不需要有多大，只是多大都可以。通常来说，指的是超过观察者的观察能力。比如数量极大以至于超过观察者可计数的极限，或者数量极其微小以至于超过观察者可辨析的极限。但是正如可计数性对应的周期性，即便是数量极大极小，仍然会出现周期性，以及周期归零的现象。这不是因为数量所描述的世界如此，而是因为我们使用数这种描述世界的工具必然如此。而我们使用这种工具，其实也是我们自身正是如此。如维特根斯坦所说，语言即世界，他说的是语言是人类以语言方式认知世界能够达到的边界。实际上数学基于人类的计数能力，则是人类以数量方式认知世界能够达到的边界。换句话说，包括周期性和可计数性，都是人类自身认知世界的边界。这也意味着，超于这个边界，就是人类能力之外的事情，而那个状态是大多数情况下都不知道的。

既然以数学方式认知世界，就必然导致基于周期性的可计数性。那么归零就成为必然，而周期的对应物就是比0小一个单位的-1，而若用这套系统作为度量系统，则必须还有一个“刻度”，这个刻度按照1和-1的几何平均数来说，就是虚数单位，

若-1意味着无限周期的大小，则它的平方根，则是这个无限周期的平方根，它显然也是无限的。于是我们就可以用这个平方根作为基本刻度，扩展出各种其它刻度来描述无限，也就是那个可以很大也可以很小的数量。

有了这个认识，让我们回到对空间的理解。我们知道万有皆是振动，振动就有频率，频率是对振动快慢的度量。而振动频率可大可小，正好就符合了不可被限制的前提条件。也就是说，我们可以用虚数单位来描述振动的快慢，以至于我们不需要知道振动到底有多快多慢。

但是我们毕竟是有限的观察者，即便不需要知道，但是仍然可以知道。我们可以知道我们自身在某个前提下，观察到振动快慢的极限。比如对于空间来说，从狭义相对论由电磁学导出可以意识到，空间振动的快慢虽然是无限的，但是可感知可用于理解构造的快慢的极限，决定于电子的振动频率，换句话说，这个无限是一个很大的数（以米秒制而言），但它仍然是有限的。根据对电磁波的进一步分析，可知它就是光速（对应的实际频率），而这个光速，对应的就是在这个前提下所谓无限频率的平方根。也就是说，对于时空而言，我们的感知极限用物理学的常数来描述，就是，

常规加速方式使得我们无法实现光速，但若能真的实现呢？这是狭义相对论要回答的问题。我们不看这个，我们看方程的右侧，就是虚数单位 ，到底和时空有啥关系。

我们知道空间是三维的，相继两个维数之间的关系是正交关系，或者说，两个维数之间相互投影为0。1和无限（体现为-1）之间显然符合相互投影为0，1在无限上的投影为0，无限在1上的投影为周期，而周期以其回环形式表现仍然为0。但若我们用1和-1相互投影，得到的却是数量上的-1。这样的两者相互投影，至多只能构成二维空间，而且这个空间是不可度量的（没有细分能力）。

可度量的至少要引入虚数单位。这时候，相互垂直的就是1和 ,1和 ，以及 和 ，其元组形式为，

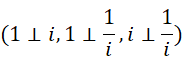
前面两个容易理解，第三个 ，难道不是 和 相反吗？因为 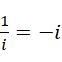，但这个时候，

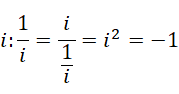
这个-1的关系，和1与-1的相互投影为0，是一样的。所以

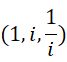
三者相互垂直。如果我们用具体的数量来描述，就更容易理解，比如我们认为

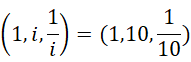
在这个三元组之中，三者互相垂直。

那么它的几何图像是什么样的呢？

我们认为这三个数值意味着三个方向的单位。比如空间有一个屏幕，按照空间笛卡尔坐标系来说， 平面，这个平面显然有两个面向，一个和 同向，一个和 反向，我们按照逆时针原则定方向，

就可以获得如下指向，

现在，我们按照从小到大的顺序，分别把三个轴的单位定为，

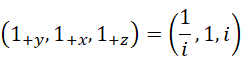
如果带入数值，就更清楚了。由此得到如下元组（tuple），

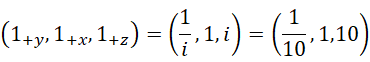
但是我们发现，这三个单位都比较大，不像是常规意义上的单位1，相反是把整个方向当作一个单位。我们暂时称其为整体单位。没关系，我们做一下比例缩放，用更小的单位来描述即可，比如我们把三个单位都缩小到一百分之一，之所以选择100，是因为本来也没有别的选择，我们把这个单位称为常规单位。

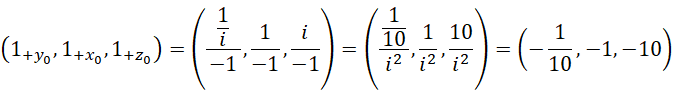
可见，用这种方法获得的单位，三个轴上正向的常规单位，正好是负向上的整体单位。也就是是说，负向上的全部，才是正向上的一个单位。

现在让我们把方向想象成一个面的面向，那么一个不小心，我们就用，

构造了三个面，如果这三个面都是边长为1的正方形，那么我们就构造了变长为1的立方体的连续三个面。而同时，用，

构造了另外三个面。有了这六个面，一个立方体就构造成了。

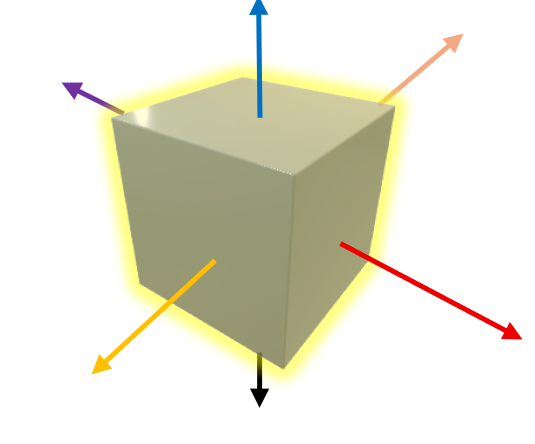
正如你所见的，观察者最多能同时看到一个立方体的三个面，这也是物体总是体现为三维的原因。这里的面并不重要，重要的是面向，或者方向。所以我们可以把这个立方体向着无限的方向缩小，就变成了只有坐标轴的空间坐标系。

下面我们可以具体的对颜色和数量进行一下对应。比如红色对应 ，那么紫色就对应于 ，以此类推。现实的空间，这个三个方向，不是绑定在具体的数量上的。而是每一个以颜色表示的方向，都同时对应于六种可能性，

所以现实的立方体中的任何一个面向，都是6个频率中心的复合。如果再考虑这个立方体的“里面”，那就是9个频率中心的复合，

如果“里外倒置”也成立，则是12个频率中心的复合，

我们应当按照最开始的做法，把这些频率中心用虚数单位的幂次进行排列（可能连续的两个幂次的方向并不连续），

其中0次幂重复，就剩下11个频率中心，

这就构成了一个三维空间中每个面都有里外两个面向，一共六个面的立方体。它由11个连续的频率中心构成。若考虑频率中心也可以连续或者不连续偏移，我们就可以得到，

如果考虑首尾闭合，则是10个连续的频率中心，此时，

不难看出，当每个面向只对应于一个单一的频率，如果r是代表频率的实数，那么随着r的增大，这个立方体就会体现出旋转并变小的过程；而旋转并变小的过程，也就意味着频率的提升，同理旋转并变大的过程，则意味着频率的下降。而这种旋转，是绝对的（参考火车和地面的相对运动，火车的运动是需要消耗能量的，而地面的相对运动不需要消耗能量，至少火车运动的相对结果）。

回到常规几何和物理空间，为什么我们的世界是三维的，因为我们没法同时看到三个以上的方向（其它平行方向上的，两个指向后面，一个藏在里面）。更根本上来说，虚数单位（10）只能把无限分成两段，而同一个单位（1）向上一段（10）向下一段（1/10）就是三个单位层次而向上和向下的极限构成的就是这个无限空间本身（100）。

有了这个标架之后，你可以考虑基于这个基础，略微做一点变化。比如x方向上，增加一丁点，因为频率的中心点移动了，频率上下范围不变，那么y方向上也会跟着变一丁点，同理z方向上也会跟着变一丁点。但是三个方向上的权重不同，比如x方向上增加0.1，y方向上就相当于增加了一个周期，而z方向上几乎没有变化。如果增加的是0.05，y方向上就相当于增加了半个周期，而z方向上增加的更少。这就是上面所说的提升（下降）导致旋转的解释。

那么其它对这个立方体的操作应当如何实现呢？比如说让它平移。在任何一个整方向上的非旋转性平移，实际上都是要求”里外里外”四个面的协同操作。比如让正方向的里外两个面的单位小于负方向的里外两个面的单位。或者让四个面的单位大小来回交替。形成在特定方向上的蠕动。大多数时候并不需要对整体进行提频或者降频。当最低的层面或者最高的层面对应的频率中心移出环境的频率中心上下限构成的范围，这个立方体就不再存在于当前环境中了。

所以总的来说，就是这11根“琴弦”，要怎么弹奏，就决定了这个正方体或者座标架，与其环境的相对位置和相对运动的状态。

去掉重复的0次，我们得到了11个维数。这似乎已经足够了。但是实际上r的偏移范围并不受到限制，也就是说，我们可以考虑两个连续的11个维数，重复中间6个维数（12的一半），总共就是，

个维数，而这正是广义相对论的二阶偏微分方程的个数（本来一阶就够了，二阶是因为需要度量的基准）。

并不是说，只有11个维数就够了，而是11个维数，重复一半的话，至少能够保持座标架的连续可变，以至于能够符合广义相对论所描述的“在弯曲空间中自动运动”的要求。

这个立方体其实是可以具有任意维数的。

由于频率复合的普遍存在，r是可以趋向无穷的。也就是说，向着更高频率的方向，所有一切振动频率最终都会在极高频率复合。也就是说，在更高的频率上，低频的两点实际上是一点在低频上的投射。由于这种里外里的方式总可以有“更里面”，所以可以认为，量子纠缠中相距甚远的超距作用，本质就是在“更里面”的频段上的共振效应。

而根据频率假说，所有一切都在至高的频率上合为一体。

所以地平学说并不是没有半点道理的胡说八道，而是另一个视角之下的对世界构成的认识。而这个认识的极限，阐述为“我心即世界”，也是可自然导出的结果。时空中的任意一点，按照频率向上溯源，都会到达同一个地方，就是至高的振动频率。当然这个频率也是无法被限制的。

现在让我们考虑导线中运动的电流。电流的运动构成一个维数，比如x轴的单位1，它是一个方向。那么这个方向就构成一个面向。在这个面向上就可以构造结构。比如说这个单位1是不断增大的，那么这个结构就是旋转的。就像x轴的单增导致y和z的同时单增。现在假定x是单位1，y是1/10，z是10，那么对于x的微小单增就会导致y方向的旋转，以及z方向上的不变。

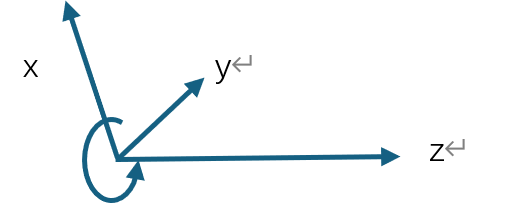
这里说的的y方向的旋转是y本身的旋转，不是绕着y的旋转。是xoy平面绕着z轴发生旋转。此时y的尺度是x的1/0，是z的1/100，但也意味着它的频率是x的10倍，z的100倍。这里的x并不需要画出，只当作是运动电荷的频率逐渐变化的体现，而不是时空长度变化的体现。有了这个理解，实际上我们就可以认为，由电荷频率单增（或者单减）导致的空间旋转，就是磁场。其单位长度为电荷长度的 倍，频率为电荷频率的 倍。有了这个认识，现在让我们看看磁场同极相斥的情况，

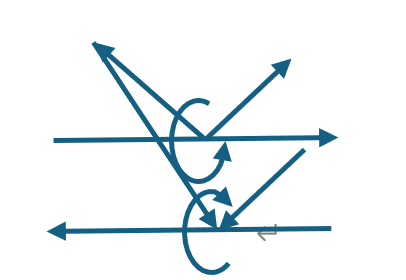
由于x方向相反，导致y和z的方向都相反。z的方向相反不影响磁场，y的方向相反也并不影响磁场，因为y的方向本来就是旋转的。但是从数量上看，y的方向相反意味着旋向也相反，这就导致了同一个频率中心x，对于特定点上的频率到底是提升还是下降出现了冲突。这个冲突反过来影响两个x，一个提升的，一个下降的，就造成了无法提升也无法下降。这就消灭了电流的方向。但是电流的方向是由各自的电源决定的。所以那个点必须提升或者下降，结果就是那些可以提升可以下降的成为了两个电流各自选择的新的频率的振动，而那些新的振动必定远离这个交汇点。反过来这个远离的效果又反向影响了两个电流，使得它们的中心彼此远离，这就形成了相斥的效果。这里远离的概率大于平行的概率。

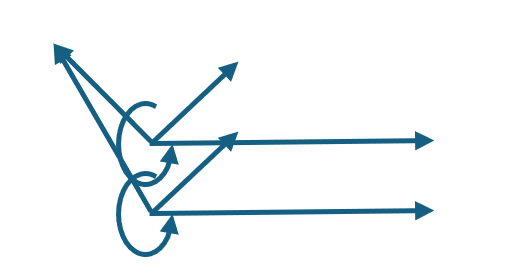
反过来说，两个电流x，同增同减，则产生相同方向的z，以及y在交汇点上同增同减。无论同增同减都是没有矛盾的。都可以选择一个更高或者更低频率的振动。并且两者更为靠近，也都是成立的。而且靠近的概率大于平行的概率。

相吸或者相斥，并不需要x的增减。但是若x没有增减，y轴不会旋转，两个存在于不同层面上的x也不会在y上相遇。这也隐含了两个x可能根本上就具有不同的基础，比如一个是100基础上的1，一个是200基础 上的1。因为在只有频率这个度量的前提下，两个不同的电子，只能具有两个不同的频段。而具有相同频段的，都是同一个电子。

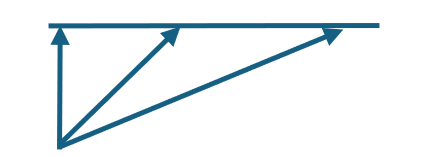
当单位变大的时候，就产生旋转效应，如图所示。若观察者认为起点相同，那么更长的整体单位只能在倾斜的情况下，才能和原来的单位对齐。而如果单位缩小，则若以缩小的一方为基准，原来未变的一方则会显得增大，也同样产生旋转效应。如果某个转动，是一切都围绕这个惯性系转动，那么它必然是缩小的一方。或者说，频率提升的一方。所以不难导出，地球的频率是提升的，太阳的频率是提升的，一切星体星云的频率都是提升的。因为在它们的视角来看，一切都是围绕它们转的。如果它们的频率下降，直到看一切都不旋转，它们就成了宇宙的背景，但这不叫熵增或者热寂。