前言

在这里插入图片描述

题解

睿抗机器人开发者大赛CAIP-编程技能赛-历年真题汇总

2021 RoboCom 世界机器人开发者大赛-本科组（复赛）解题报告

感觉这个T1特别有意思，非典型题，着重推演下结论。

T2是一道玄学题，但是涉及一些优化技巧。

T3这类题，vp的价值并不大，但是符合睿抗的出题风格。

T4是睿抗特别喜欢的最短路径题，但是一来题目有坑点，二来真的太耗时间了，T_T。

7-1 冒险者分队

分值： 20分

思路：解方程组 + 中位数定律

题意省流：

三个数a, b, c 通过如下操作变为 d, e, f

选择某个数+40，其余两数-20
选择某个数-40，其余两数+20

求最小的操作步骤数，如不存在则返回-1

这类贪心题挺难，如何证明，以及写对挺难得。

前置论点:

某个数不可能同时存在+40，又-40的操作，因为两两抵消属于无用功，要满足最小步骤，必然只有一个操作方向
a + b + c = d + e + f

$令x1，x2，x3分别为a,b,c对应40的操作次数,(x1,x2,x3∈Z){令x_1，x_2，x_3分别为a, b, c 对应40的操作次数, (x_1, x_2, x_3 \in Z) }$

${若 x_k > 0, 说明 +40操作 x_k次}$
${若 x_k < 0, 说明 -40操作 |x_k|次}$

构建对应的三元一次方程组,

${40x1−20x2−20x3=d−a=y1−20x1+40x2−20x3=e−b=y2−20x1−20x2+40x3=f−c=y3\left\{\begin{matrix} 40x_1 - 20x_2 - 20x_3 = d - a = y_1\\ -20x_1 + 40x_2 - 20x_3 = e - b = y_2\\ -20x_1 - 20x_2 + 40x_3 = f - c = y_3 \end{matrix}\right.$

$求 f(x_1, x_2, x_3) = |x_1| + |x_2| + |x_3| 最小$

该方程组的秩为2，没法解, 但是可以把 $x_1, x_2表示为x_3的形态$

方程组进行变换为，可求得

${x1=(2y1+y2)/60+x3x2=(2y2+y1)/60+x3\left\{\begin{matrix} x_1 = (2y_1 + y_2) / 60 + x_3 \\ x_2 = (2y_2+y_1) / 60 + x_3 \end{matrix}\right.$

进而
$f(x_1,x_2, x_3) = |x_1| + |x_2| + |x_3|$
$⇒f(x1,x2,x3)=∣x3+(2y1+y2)/60∣+∣x3+(2y2+y1)/60∣+∣x3∣\Rightarrow f(x_1,x_2, x_3) = |x_3+(2y_1 + y_2) / 60| + |x_3 + (2y_2+y_1) / 60| + |x_3|$
$⇒f(x1,x2,x3)=∣x3−z1∣+∣x3−z2∣+∣x3−z3∣\Rightarrow f(x_1,x_2, x_3) = |x_3- z_1| + |x_3 - z_2| + |x_3 - z_3|$

求这个得最小值，不就是 中位数定律 吗？

取 ${ z_1=-(2y_1 + y_2) / 60 , z_2=-(2y_2+y_1) / 60, z_3=0 } 三个数的中间值，带入f(x_1, x_2, x_3) 即可$

当然这边的额外条件是

保证 $2y_1 + y_2) / 60 , -(2y_2+y_1) / 60$ 需为整数

#include <bits/stdc++.h>using namespace std;int64_t median(int64_t a, int64_t b, int64_t c, int64_t x) {return abs(x - a) + abs(x - b) + abs(x - c);
}int main() {int t;cin >> t;while (t-- > 0) {int64_t a, b, c;int64_t d, e, f;cin >> a >> b >> c;cin >> d >> e >> f;if (a + b + c != d + e + f) {cout << -1 << "\n";continue;}int64_t y1 = d - a;int64_t y2 = e - b;if ((2*y1 + y2) % 60 != 0 || (2 * y2 + y1) % 60 != 0) {cout << -1 << "\n";continue;}// 方程组求解int64_t z1 = (2 * y1 + y2) / 60;int64_t z2 = (2 * y2 + y1) / 60;vector<int64_t> tmp = {-z1, -z2, 0};sort(tmp.begin(), tmp.end());// 中位数定律int64_t res = median(-z1, -z2, 0, tmp[1]); // tmp[1]为中点cout << res << "\n";}return 0;
}

7-2 拼题A打卡奖励

思路： 0-1背包

时间复杂度 $O(N*M)=O(365*24*60*1000)=O(5*10^8)$

#include <bits/stdc++.h>using namespace std;int main() {int n, M;cin >> n >> M;vector<int> arr(n), brr(n);for (int &x: arr) cin >> x;for (int &x: brr) cin >> x;vector<int> dp(M + 1);for (int i = 0; i < n; i++) {for (int j = M - arr[i]; j >= 0; j--) {dp[j+arr[i]] = max(dp[j+arr[i]], dp[j] + brr[i]);}}cout << *max_element(dp.begin(), dp.end()) << "\n";return 0;
}

纯数组的0-1背包，其实是可以直接冲的。

这题的玄就在玄在:

g++提交，tle
clang++提交， ac

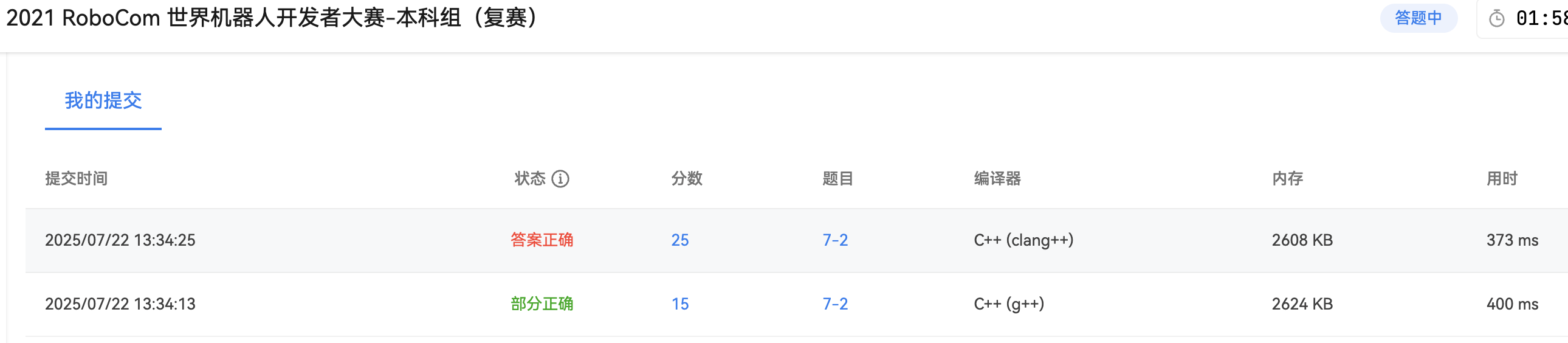
在这里插入图片描述
那这题关键点在于什么呢？

每次打卡花费的时间为 $mi≤600m_i \le 600$

即总的容量为： ${Q = min(n*600, M)}$ ，时间复杂度变为 $O (n * Q)$ ，存在收益

压缩容量遍历（尤其是早期）

可以对打卡时间从小到大排序，然后容量上限逐步提高

#include <bits/stdc++.h>using namespace std;int main() {int n, M;cin >> n >> M;vector<array<int,2>> cards(n);for (int i = 0; i < n; i++) {cin >> cards[i][0];}for (int i = 0; i < n; i++) {cin >> cards[i][1];}// 第一个优化点int Q = min(n * 600, M);vector<int> dp(Q + 1);// 第二个优化点, 按时间从小到大排序sort(cards.begin(), cards.end(), [](auto &a, auto &b) {return a[0] < b[0];});int tot = 0;for (int i = 0; i < n; i++) {int v = cards[i][0], w = cards[i][1];// 逐步放大范围tot = min(tot + v, Q);for (int j = tot - v; j >= 0; j--) {dp[j+v] = max(dp[j+v], dp[j] + w);}}cout << *max_element(dp.begin(), dp.end()) << "\n";return 0;
}

结果对比：
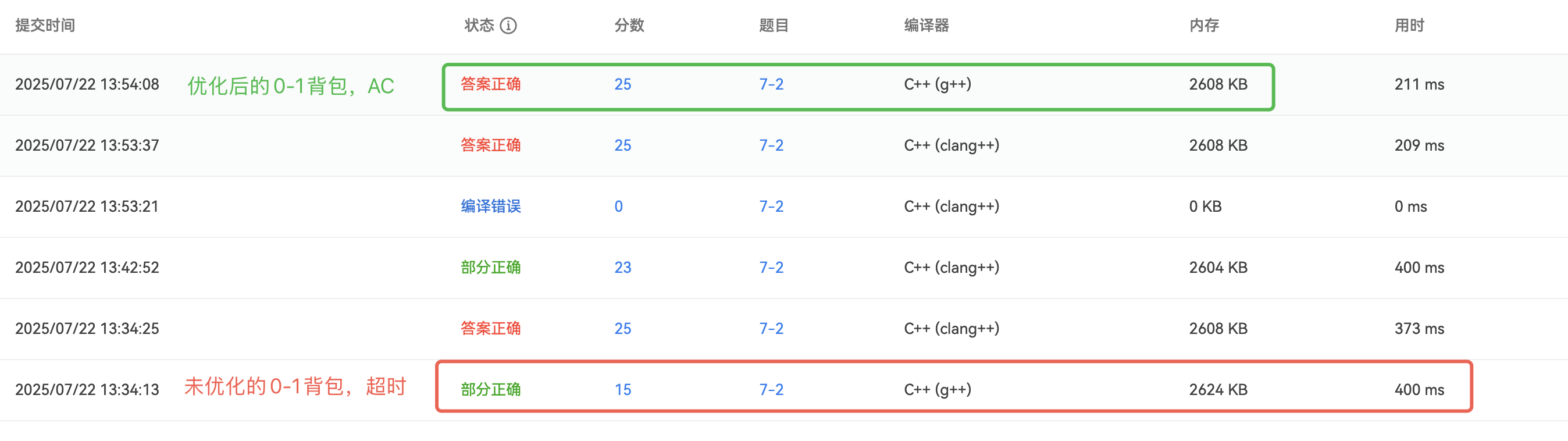
在这里插入图片描述

7-3 快递装箱

分值: 25分
思路：建模+模拟
知识点：双端队列
前置的知识点：

一个数组，整体右移一位，其实是需要借助一个临时变量来实现，这边也借助了这个技巧

根据题意，A，B，C，D点只能存一个包裹，但是A额外配置一个等待队里

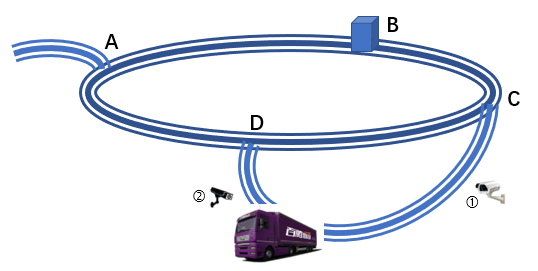
在这里插入图片描述
包裹定义

struct Pack {int w = 0; // 快递/快递包的质量bool boxed = false; // 是否打包
};

这里面有歧义的地方

D点位在已经没有货物过来了，则停止当前的装箱工作，做自检

如何解读这个呢？

从D点的角度出发，C点没有货物过来
所有快递都在传输带上了，最后一个新快递刚到A点，激活该策略
所有快递都在传输带上了，其最后一个快递要么出列，要么重新回到A点，激活该策略

这题，完全没说明这点，而且有case解说，但是没有消除歧义。

目前按2,3去解释，能完全AC，但是两者在特定case下，结果又不一样。


#include <bits/stdc++.h>using namespace std;struct Pack {int w = 0;bool boxed = false; // boxed
};int main() {int n, wmax, w1, w2;cin >> n >> wmax >> w1 >> w2;vector<int> arr(n);for (int &x: arr) cin >> x;int ans1 = 0, ans2 = 0;deque<Pack> A;Pack a, b, c, d;bool ae = false, be = false, ce = false, de = false;auto loop_event = [&](bool flag, int x) -> bool {bool update = false;Pack tmpA;bool tmpAe = false;if (flag) {if (!A.empty()) {Pack top = A.front();if (top.w + x <= wmax) {top.w += x;tmpA = top;tmpAe = true;A.pop_front();} else {tmpA = {x, false}; tmpAe = true;}} else {tmpA = {x, false}; tmpAe = true;}} else {if (!A.empty()) {tmpA = A.front(); A.pop_front();tmpAe = true;}}if (de) {if (ce) {if (!c.boxed && d.w + c.w <= wmax) {d.w += c.w;} else {if (d.w > w2) {ans2++;} else {A.push_back(d);}d = c;d.boxed = true;}ce = false;} else {if (!flag) {// 如果没有新货源，则需要自检并打包/推进，不允许等待if (d.w > w2) {ans2++;update = true;} else {A.push_back(d);}de = false;}}} else {if (ce) {d = c;de = true;d.boxed = true;ce = false;} else {de = false;}}if (be) {if (b.w > w2) {ans1++;update = true;ce = false;} else {c = b;ce = true;}be = false;} else {ce = false;}if (ae) {b = a;be = true;if (b.w > w1) {b.boxed = true;}ae = false;} else {be = false;}a = tmpA;ae = tmpAe;return update;};for (int x: arr) {loop_event(true, x);}int loop = n - ans1 - ans2 + 4;while (loop-- > 0) {if (loop_event(false, -1)) {loop = n - ans1 - ans2 + 4;}}vector<int> left;while (!A.empty()) {left.push_back(A.front().w);A.pop_front();}if (ae) left.push_back(a.w);if (be) left.push_back(b.w);if (ce) left.push_back(c.w);if (de) left.push_back(d.w);sort(left.begin(), left.end());cout << ans1 << " " << ans2 << " " << left.size() << "\n";int mz = left.size();if (mz == 0) cout << "None\n";else {for (int i = 0; i < mz; i++) {cout << left[i] << " \n"[i == mz - 1];}}return 0;
}

期间参考了 小哈里 博客：
2021 RoboCom 世界机器人开发者大赛-本科组（复赛）-T3代码

感觉用四个队列，代码更简洁些，两者另一个差异：规则解读上D点，没有新货物来时, D点的货物该怎么操作。

构造一个特定的case
输入：

5 100 50 80
60 88 88 20 61

输出(按2解释)

2 0 3
20 60 61

输出(按3解释)

2 0 2
61 80

两份代码都能AC，但是特定case输出不一样，睿抗数据还是弱了。

毫无疑问，这是一道好题，但是睿抗的出题，总会整一些歧义点，然后让你拿不了满分，同时使得你陷入到处找茬/猜猜乐的窘境。

7-4 塔防游戏

分值: 30分
思路: dijkstra 板子题

需要逆向从目标点出发，到达僵尸所在地，然后在按时间模拟

注意点:

只要击毁大本营就是胜利，不需要达到大本营地
只要击毁堡垒，才能到达该格子，前后顺序不能相反
当3个僵尸同时攻打某个防御值为2的堡垒，该堡垒消失的同时，3个僵尸都会被扣1滴血 出处参考
每个僵尸军团不能合并，需要维护其独立性

路径规划

单纯的dijkstra板子即可

时间复杂度为 $O (n * m * l o g (n * m))$

路线模拟

每个军团按单位时间挪动一个位子

时间复杂度为 $O (T * 2 * (n + m))$


#include <bits/stdc++.h>using namespace std;const int inf = 1e8;struct ST {int w = inf;int s = 0;bool operator<(const ST &o) const {if (w != o.w) return w < o.w;return s < o.s;}
};struct Step {int y, x;ST st;bool operator<(const Step& o) const {return o.st < st;}
};int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int n, m, T;cin >> n >> m >> T;vector<vector<int>> g(n + 2, vector<int>(m + 2));vector<array<int, 3>> js;int ty = -1, tx = -1;for (int i = 0; i <= n + 1; i++) {for (int j = 0; j <= m + 1; j++) {cin >> g[i][j];if (g[i][j] < 0) {ty = i; tx = j;g[i][j] = -g[i][j];} else if ((i == 0 || i == n + 1) && j != 0 && j != m + 1 && g[i][j] > 0) {js.push_back({i, j, g[i][j]});g[i][j] = 0;} else if (i != 0 && i != n + 1 && (j == 0 || j == m + 1) && g[i][j] > 0) {js.push_back({i, j, g[i][j]});g[i][j] = 0;} else if (i == 0 || j == 0 || i == n + 1 || j == m + 1) {g[i][j] = inf;}}}// 逆向dijkstravector<vector<ST>> dp(n + 2, vector<ST>(m + 2));vector<vector<int>> source(n + 2, vector<int>(m + 2, -1));priority_queue<Step, vector<Step>> pq;pq.push({ty, tx, {0, 0}});dp[ty][tx] = {0, 0};int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};while (!pq.empty()) {Step step = pq.top(); pq.pop();int y = step.y, x = step.x;if (dp[y][x] < step.st) continue;for (int i = 0; i < 4; i++) {int ny = y + dirs[i][0];int nx = x + dirs[i][1];if (ny >= 0 && ny <= n + 1 && nx >= 0 && nx <= m + 1) {ST tmp = {dp[y][x].w + g[ny][nx], dp[y][x].s + 1 + g[ny][nx]};if (tmp < dp[ny][nx]) {dp[ny][nx] = tmp;if (ny != 0 && ny != n + 1 && nx != 0 && nx != m + 1) pq.push(Step{ny, nx, tmp});source[ny][nx] = y * (m + 2) + x;}}}}while (T-- > 0) {set<array<int, 2>> hash;vector<array<int, 3>> njs;for (auto &[y, x, w]: js) {int d = source[y][x];int ny = d / (m + 2), nx = d % (m + 2);if (g[ny][nx] > 0) {g[ny][nx]--;hash.insert({ny, nx});if (w > 1) njs.push_back({y, x, w - 1});} else if (hash.count({ny, nx}) != 0) {if (w > 1) njs.push_back({y, x, w - 1});} else {njs.push_back({ny, nx, w});}}if (g[ty][tx] <= 0) break;js.swap(njs);}for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {if (i == ty && j == tx) {cout << min(0, -g[i][j]) << " \n"[j == m];} else {cout << g[i][j] << " \n"[j == m];}}}if (g[ty][tx] <= 0) {cout << "Game Over\n";}return 0;
}