二叉搜索树（Binary Search Tree，简称 BST）是一种特殊的二叉树，因其高效的查找、插入和删除操作，成为计算机科学中最重要的数据结构之一。BST 的核心特性是 “左小右大”，这一特性使其在数据检索、排序和索引等场景中发挥着关键作用。

二叉搜索树的定义与核心性质

定义

二叉搜索树是一种二叉树，其中每个节点的左子树中所有节点的值小于该节点的值，右子树中所有节点的值大于该节点的值。这一性质被称为 “左小右大” 原则，且该原则对所有子树都成立。

形式化定义：

对于 BST 中的任意节点node，满足：

左子树中所有节点的值 < node.val

右子树中所有节点的值 > node.val

左子树和右子树本身也是二叉搜索树

核心性质

中序遍历特性：BST 的中序遍历（左→根→右）结果是严格升序的。这是 BST 最核心的性质，也是解决多数 BST 问题的关键。
查找效率：在平衡的 BST 中，查找、插入、删除操作的时间复杂度为O(logn)；在最坏情况下（如退化为链表），时间复杂度为O(n)。
唯一性：给定一组数据，可能存在多个 BST 结构，但中序遍历结果唯一（即数据的升序序列）。

结构图示

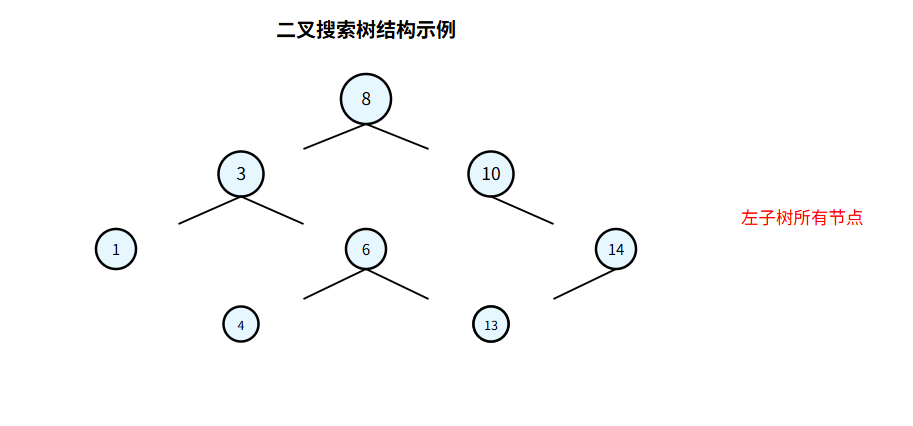
`二叉搜索树的基本操作`

`查找操作`

思路

利用BST“左小右大”的性质，从根节点开始：
- 若目标值等于当前节点值，返回该节点。
- 若目标值小于当前节点值，递归查找左子树。
- 若目标值大于当前节点值，递归查找右子树。
- 若遍历到空节点，返回`null`（未找到）。

`实现代码`

class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) {val = x;}}public TreeNode searchBST(TreeNode root, int val) {if (root == null || root.val == val) {return root;}return val < root.val ? searchBST(root.left, val) : searchBST(root.right, val);}

插入操作

思路：插入过程类似查找，找到合适的空位置插入新节点：

若当前节点为空，创建新节点返回。

若插入值小于当前节点值，递归插入左子树。

若插入值大于当前节点值，递归插入右子树。

（BST 通常不允许重复值，若需处理重复值，可约定插入右子树）

插入过程图示

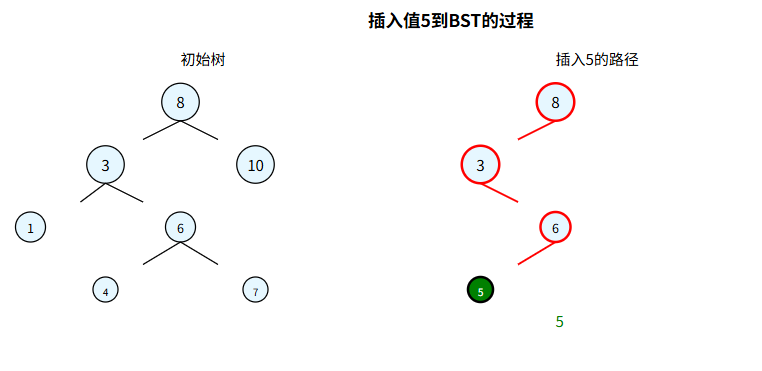
实现代码

public TreeNode insertIntoBST(TreeNode root, int val) {if (root == null) {return new TreeNode(val); // 找到插入位置}if (val < root.val) {root.left = insertIntoBST(root.left, val); // 插入左子树} else {root.right = insertIntoBST(root.right, val); // 插入右子树}return root;}

删除操作

删除操作是 BST 中最复杂的操作，需根据节点的子树情况分三种处理：

叶子节点（无左右子树）：直接删除，返回null。
单子树节点（只有左或右子树）：删除节点，用子树替代其位置。
双子树节点（有左右子树）：
找到该节点的前驱（左子树中最大节点）或后继（右子树中最小节点）。
用前驱（或后继）的值替换当前节点的值。
递归删除前驱（或后继）节点。

删除过程图示

（删除节点 6）：

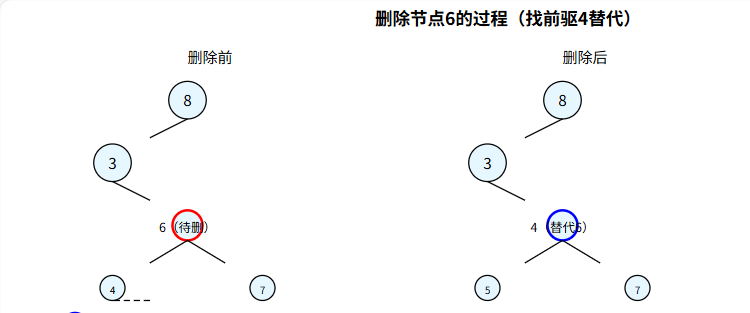
实现代码：

public TreeNode deleteNode(TreeNode root, int key) {if (root == null) {return null; // 未找到待删节点}if (key < root.val) {root.left = deleteNode(root.left, key); // 递归删除左子树} else if (key > root.val) {root.right = deleteNode(root.right, key); // 递归删除右子树} else {// 找到待删节点，分三种情况if (root.left == null) {return root.right; // 无左子树，用右子树替代} else if (root.right == null) {return root.left; // 无右子树，用左子树替代} else {// 有左右子树，找左子树最大节点（前驱）TreeNode predecessor = findMax(root.left);root.val = predecessor.val; // 替换值root.left = deleteNode(root.left, predecessor.val); // 删除前驱}}return root;}// 查找左子树最大节点（最右节点）private TreeNode findMax(TreeNode node) {while (node.right != null) {node = node.right;}return node;}

LeetCode 例题实战

例题 1：98. 验证二叉搜索树（中等）

题目描述：给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。有效 BST 定义为：
节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例：

输入：root = [2,1,3]

输出：true（1<2<3，符合BST）

输入：root = [5,1,4,null,null,3,6]

输出：false（4的左子树有3<4，但4<5不成立）

解题思路

利用 BST 中序遍历为升序的特性，或递归检查每个节点的左右边界：

中序遍历法：中序遍历 BST，若结果非严格升序，则不是有效 BST。
递归边界法：为每个节点设置上下边界（low和high）：
根节点的边界为(-∞, +∞)。
左子树节点的边界为(low, root.val)。
右子树节点的边界为(root.val, high)。
若节点值超出边界，则无效。

方法 2（递归边界法）Java 代码

class Solution {public boolean isValidBST(TreeNode root) {return isValid(root, Long.MIN_VALUE, Long.MAX_VALUE);}private boolean isValid(TreeNode node, long low, long high) {if (node == null) {return true; // 空树是有效BST}// 节点值必须在(low, high)范围内if (node.val <= low || node.val >= high) {return false;}// 左子树边界：(low, node.val)，右子树边界：(node.val, high)return isValid(node.left, low, node.val) && isValid(node.right, node.val, high);}}

复杂度分析

时间复杂度：O (n)，遍历所有节点一次。

空间复杂度：O (n)，递归栈深度最坏为 n（退化为链表）。

例题 2：108. 将有序数组转换为二叉搜索树（简单）

题目描述：给你一个整数数组 nums ，其中元素已经按升序排列，请你将其转换为一棵高度平衡的二叉搜索树。高度平衡的二叉树是指每个节点的左右两个子树的高度差的绝对值不超过 1。

示例：

输入：nums = [-10,-3,0,5,9]

输出：[0,-3,9,-10,null,5]（或其他平衡BST结构）

解题思路

利用 BST 中序遍历为升序的逆过程：

选中间元素为根：平衡 BST 的根应是数组中间元素，确保左右子树大小均衡。
递归构建：
左子树由数组左半部分构建。
右子树由数组右半部分构建。
递归终止条件：数组为空时返回null。

构建过程图示

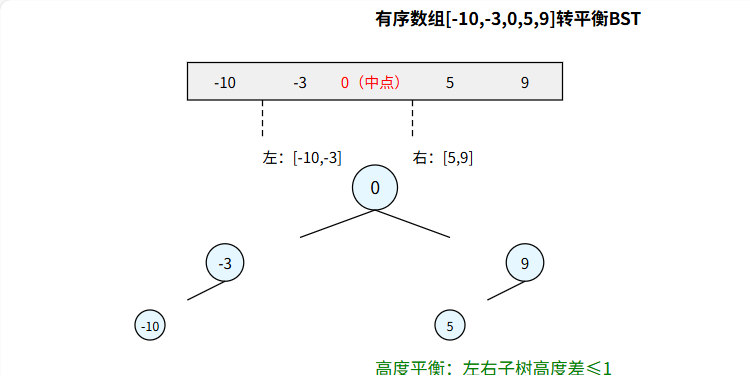
代码实现

class Solution {public TreeNode sortedArrayToBST(int[] nums) {return build(nums, 0, nums.length - 1);}private TreeNode build(int[] nums, int left, int right) {if (left > right) {return null; // 递归终止}// 选择中间元素作为根（平衡关键）int mid = left + (right - left) / 2;TreeNode root = new TreeNode(nums[mid]);// 递归构建左右子树root.left = build(nums, left, mid - 1);root.right = build(nums, mid + 1, right);return root;}}

复杂度分析

时间复杂度：O (n)，每个元素构建一个节点。

空间复杂度：O (logn)，递归栈深度为平衡树的高度 logn。

考研 408 例题解析

例题 1：概念辨析题（选择题）

题目：下列关于二叉搜索树的叙述中，正确的是（）。
A. 二叉搜索树的中序遍历序列一定是递增的
B. 二叉搜索树中任意节点的左子树高度一定小于右子树高度
C. 对二叉搜索树进行前序遍历，再根据前序遍历序列可以唯一重构该 BST
D. 在二叉搜索树中查找某元素的时间复杂度一定是 O (logn)

答案：A

解析：

A 正确：BST 的核心性质就是中序遍历为严格递增序列。

B 错误：BST 不要求左右子树高度平衡（平衡 BST 如 AVL 树才要求）。

C 错误：前序遍历序列无法唯一重构 BST（如前序 [2,1,3] 和 [2,3,1] 可能对应不同 BST）。

D 错误：在最坏情况下（退化为链表），查找时间复杂度为 O (n)。

例题 2：算法设计题（408 高频考点）

题目：设计一个算法，在二叉搜索树中找出第 k 小的元素，并分析算法的时间复杂度。

解题思路

利用 BST 中序遍历为升序的特性，中序遍历的第 k 个元素即为第 k 小元素：

递归中序遍历：记录遍历顺序，当计数达到 k 时返回当前节点值。
迭代中序遍历：用栈模拟中序遍历，弹出第 k 个节点时返回其值。

方法 2（迭代法）实现代码

public int kthSmallest(TreeNode root, int k) {Deque<TreeNode> stack = new ArrayDeque<>();TreeNode curr = root;int count = 0;while (curr != null || !stack.isEmpty()) {// 左子树入栈while (curr != null) {stack.push(curr);curr = curr.left;}// 弹出栈顶（中序遍历的当前节点）curr = stack.pop();count++;if (count == k) {return curr.val; // 找到第k小元素}// 处理右子树curr = curr.right;}return -1; // 无效输入（k超出范围）}

复杂度分析

时间复杂度：O (h + k)，h 为 BST 高度，最坏为 O (n + k)（链表），平均为 O (logn + k)。

空间复杂度：O (h)，栈存储的节点数为树的高度。

二叉搜索树的扩展与应用

实际应用场景

数据库索引：MySQL 的 B + 树索引基于 BST 扩展，支持高效范围查询。

有序映射 / 集合：Java 中的TreeMap和TreeSet底层为红黑树（一种平衡 BST）。

排序与检索：利用 BST 的插入和中序遍历实现排序，时间复杂度 O (nlogn)。

与其他树结构的关系

树结构	特点	适用场景
二叉搜索树（BST）	左小右大，中序升序	基础检索、排序
AVL 树	平衡 BST，左右高差≤1	需严格平衡的场景
红黑树	近似平衡 BST，黑高一致	插入删除频繁的场景（如集合）
B + 树	多路 BST，叶子节点成链表	数据库索引

考研 408 备考要点

核心考点：BST 的定义与性质、中序遍历特性、插入 / 删除 / 查找操作。

重点掌握：

利用中序遍历解决 BST 相关问题（如验证 BST、找第 k 小元素）。
插入和删除操作的递归实现，尤其是删除时的节点替换逻辑。
BST 与平衡树的区别，以及时间复杂度分析。

常见错误：
- 忽略 BST 中 “严格大于 / 小于” 的约束（允许等于时需明确约定）。

- 删除节点时未正确处理双子树情况，导致 BST 性质被破坏。

总结

二叉搜索树作为一种基础且重要的数据结构，其 “左小右大” 的特性和中序遍历升序的性质，使其在数据检索和排序中有着广泛应用。本文通过 LeetCode 例题（验证 BST、有序数组转 BST）展示了 BST 的核心应用，通过考研 408 例题解析了概念辨析和算法设计思路，结合 SVG 图示直观呈现了 BST 的结构及操作过程。

掌握 BST 的关键在于：