一、初始化
不同于NSGA-II,MOEA/D在进行迭代之前需要先进行初始化,初始化的主要内容是计算个体向量权重之间的欧氏距离,并得出其邻域集合。
# 计算T个邻居
def cpt_W_Bi_T(moead):# 设置的邻居个数错误(自己不能是自己的邻居)if moead.T_size < 1:return -1# 计算权重的T_size 个邻居for bi in range(moead.W.shape[0]):Bi = moead.W[bi]# 计算欧氏距离DIS = np.sum((moead.W - Bi) ** 2, axis=1)# 根据欧氏距离排序B_T = np.argsort(DIS)# 选取T_size+1个邻居,+1是因为自己永远是和自己欧氏距离最小的B_T = B_T[1:moead.T_size + 1]# 添加到集合moead.W_Bi_T.append(B_T)除了计算邻域,还需要使用目标函数计算种群的适应度,如下:
def Creat_Pop(moead):# 创建moead.Pop_size个种群Pop = []Pop_FV = []# 合法性检查if moead.Pop_size < 1:print('error in creat_Pop')return -1# 构建集合while len(Pop) != moead.Pop_size:X = Creat_child(moead) # 创建一个个体Pop.append(X) # 将这个个体放入集合Pop_FV.append(moead.Test_fun.Func(X)) # 使用目标函数计算适应度moead.Pop, moead.Pop_FV = Pop, Pop_FV # 初始化主函数容器return Pop, Pop_FV二、迭代
在循环迭代中,对于个体pi的迭代主要分为三步:获取邻居;生成新解;更新种群。其具体流程如下面伪代码所示:
for pi in range(0,len(moead.Pop)) # 遍历集合Bi = moead.W_Bi_T[pi] # 加载pi号个体的邻居集# 随机抽取两个邻居个体ik = Bi[np.random.randint(moead.T_size)]il = Bi[np.random.randint(moead.T_size)]# 获取x,xl,xk三个个体的值(目标个体本身和随机抽取的两个邻居)Xi = moead.Pop[pi]Xk = moead.Pop[ik]xl = moead.Pop[il]# 使用上述三个个体生成新的解Y = generate_next(moead, gen, pi, Xi, Xk, Xl)cbxf_i = MOEAD_Utils.cpt_tchbycheff(moead, pi, Xi) # 计算进化前的切比雪夫距离cbxf_y = MOEAD_Utils.cpt_tchbycheff(moead, pi, Y) # 计算进化后的切比雪夫距离# 若进化后切比雪夫距离缩小就更新,否则保持原状if cbxf_y < cbxf_i:F_Y = moead.Test_Fun.Func(Y)[:] # 计算进化后个体的适应度MOEAD_Utils.update_EP_By_ID(moead, pi, F_Y) # 更新pi号个体的值为YMOEAD_Utils.update_Z(moead, Y) # 更新理想点if abs(cbxf_y - cbxf_i) > d: # 进化幅度大于阈值MOEAD_Utils.update_EP_By_Y(moead, pi) # 更新支配前沿MOEAD_Utils.update_BTX(moead, Bi, Y) # 更新邻域三、效果展示
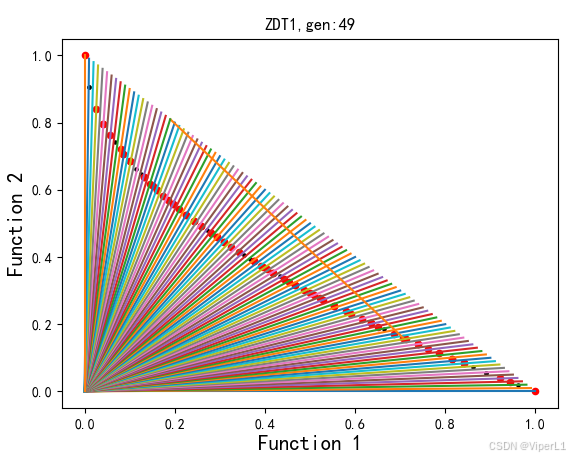


)









系统上安装 MuJoCo)


——变分自编码器详解与实现)



![[AI-video] 数据模型与架构 | LLM集成](http://pic.xiahunao.cn/[AI-video] 数据模型与架构 | LLM集成)