1冒泡排序

void BubbleSort(int* a, int n)
{int exchange = 0;for (int i = 0; i < n; i++){for (int j = 0; j < n - i - 1; j++){if (a[j] > a[j + 1]){exchange = 1;swap(&a[j], &a[j + 1]);}}if (exchange == 0){break;}}
}

每次循环都会找到最大的元素放到最后一个位置上，以此往复完成排序。
如果在某一次循环exchange变成0，说明数组已然有序，直接退出循环即可。
时间复杂度：O(N^2 )
空间复杂度：O(1)

2.快速排序

快速排序是Hoare于1962年提出的⼀种⼆叉树结构的交换排序⽅法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两⼦序列，左⼦序列中所有元素均⼩于基准值，右⼦序列中所有元素均⼤于基准值，然后最左右⼦序列重复该过程，直到所有元素都排列在相应位置上为⽌。
快速排序实现主框架：

void QuickSort(int* a, int left, int right)
{if (left >= right) {return;}//_QuickSort⽤于按照基准值将区间[left,right)中的元素进⾏划分 int meet = _QuickSort(a, left, right);QuickSort(a, left, meet - 1);QuickSort(a, meet + 1, right);
}

_QuickSort这个函数应该怎么设计呢？

2.1hoare版本找基准值

int _QuickSort(int* a, int left, int right)
{int keyi = left;left++;while (left <= right){//right:从右往左找比基准值小的while (left <= right && a[right] > a[keyi]){right--;}//left:从左往右找比基准值大的while (left <= right && a[left] < a[keyi]){left++;}if (left <= right){Swap(&a[left++], &a[right--]);}}Swap(&a[keyi], &a[right]);//与小于基准值的交换return right;
}

2.2lomuto前后指针

设计两个指针，cur指针负责遍历整个数组并找见比基准值小的并于prev指向的交换，每次两个指针都++,如果cur遇见比基准值大的prev就不动，直到遇到小于基准值的就另++prev指向的数据与cur指向的交换
在这里插入图片描述

int _QuickSort(int* a, int left, int right)
{int prev = left, cur = left + 1;int key = left;while (cur <= right){if (a[cur] < a[key] && ++prev != cur){swap(&a[cur], &a[prev]);}++cur;}swap(&a[key], &a[prev]);return prev;
}

时间复杂度：O(nlogn)
空间复杂度：O(logn)

3.非递归版本快速排序

这里就用到了我们前面实现的栈了。
我们知道，在快速排序中，数组中元素的交换是发生在找基准值这个过程中的，所以我们可以在栈中不断放入left与right.直到栈为空。

void QuickSortNorR(int* arr, int left, int right)
{ST st;STInit(&st);STPush(&st,right);STPush(&st,left);while (!STEmpty(&st)){//取栈顶两次int begini = STTop(&st);STPop(&st);int endi = STTop(&st);STPop(&st);//找基准值int keyi = _QuickSort(arr, begini, endi);if (keyi+1 < endi)//右序列[keyi+1,endi]{STPush(&st，endi);STPush(&st，keyi+1);}if (keyi -1> begini)//左序列[begini,keyi-1]{STPush(&st，keyi-1);STPush(&st，begini);}}Destroy(&st);
}

我们可以看到，这个版本中的逻辑其实也跟递归类似，都是一条路走到黑，直到序列中的left与rihgt不符合找基准值的条件。

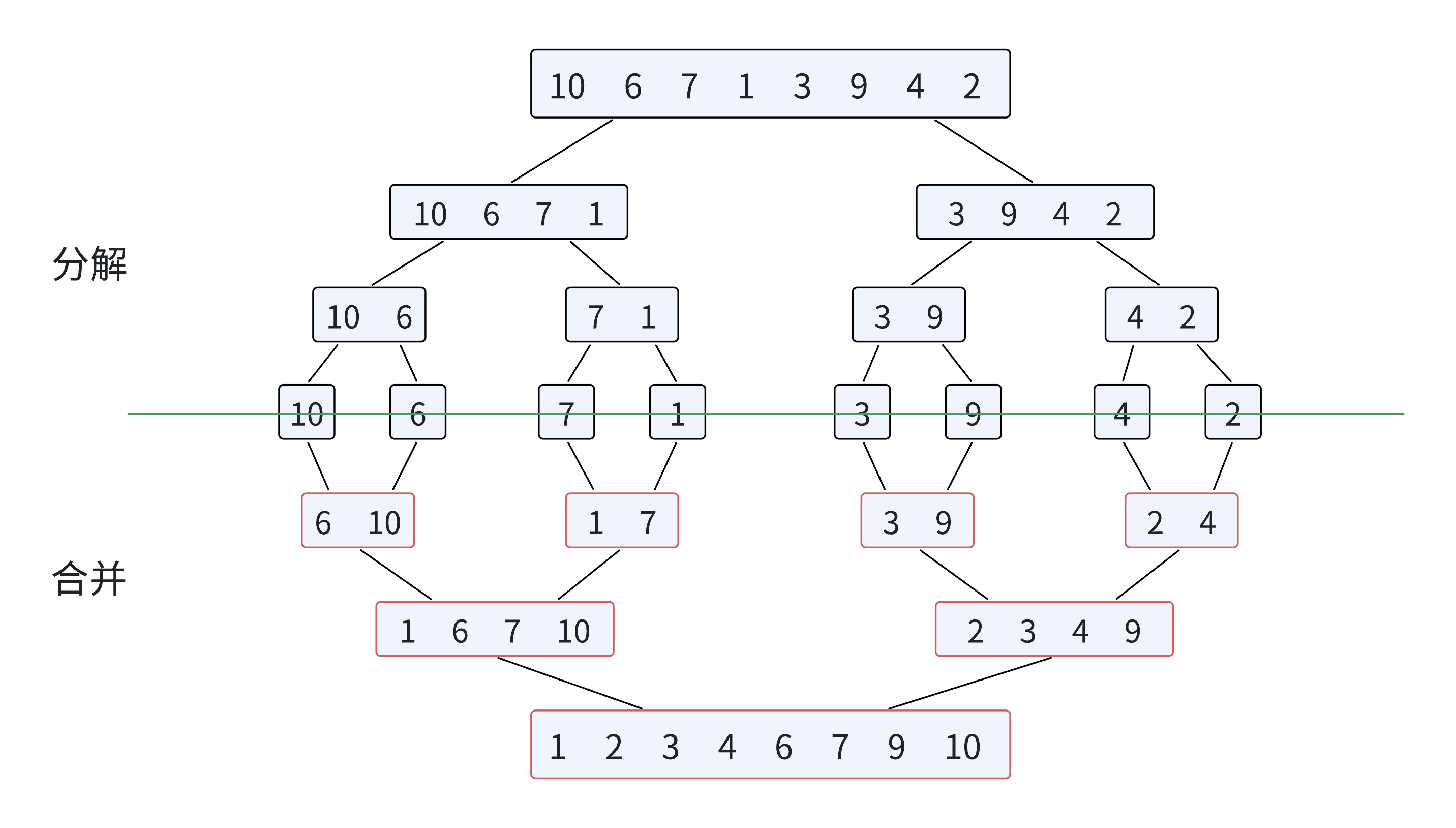
4.递归排序

这张图可以很好解释归并排序的思想，我们想要将数组拆分成多个子数组，将这多个子数组都变成有序，合并
在这里插入图片描述

void _MergrSort(int* arr, int left, int right,int*tmp)
{//分解if (left >= right){return;}int mid = (left + right) / 2;_MergrSort(arr, left, mid,tmp);_MergeSort(arr, mid + 1, right,tmp);//当程序走到这里时，[left,mid],[mid+1,right]已经变成两个有序数组//合并两个有序数组int begin1 = left;int end1 = mid;int begin2 = mid + 1;int end2 = right;int index = left;while (begin1 <= end1 && begin2 <= end2){if (arr[begin1] < arr[begin2]){tmp[index++] = arr[begin1++];}else{tmp[index++] = arr[begin2++];}}for (int i = left;i <= right;i++){arr[i] = tmp[i];}}
void MergeSort(int* arr, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);_MergeSort(arr, 0, n - 1,tmp);free(tmp);
}

时间复杂度：O(nlogn)
空间复杂度：O(n)

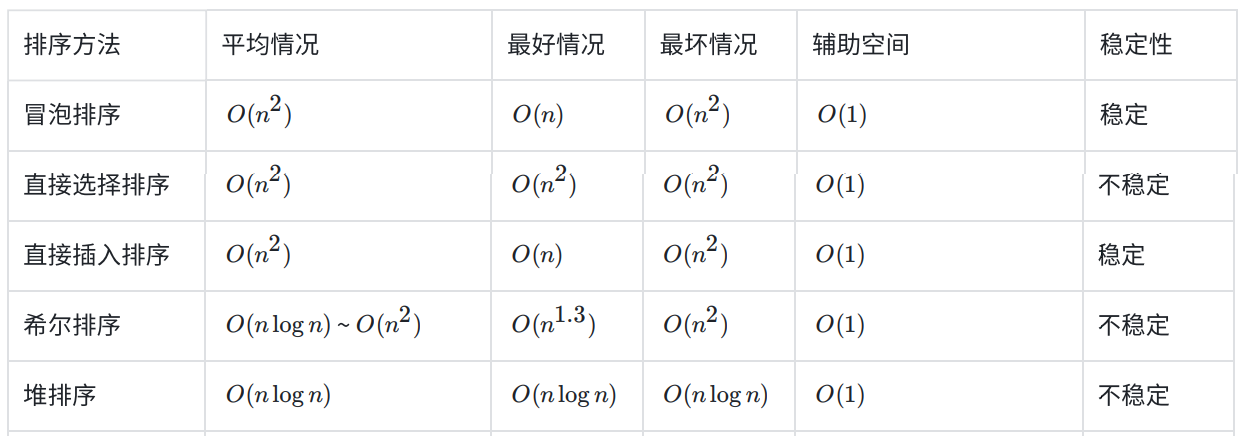
5.排序算法复杂度及稳定性分析

稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，⽽在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。
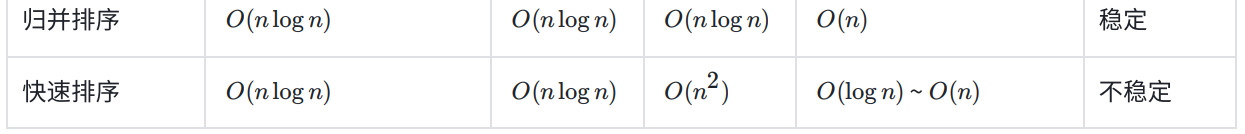
在这里插入图片描述

完
如果发现错误，欢迎打在评论区。
主页还有更多优质内容OvO