1.向量

1.1 点积（Dot Product）

1.1.1 定义

点积是在求一个标量，点积结果没有方向。
对于两个向量$\mathbf{u}=(u_1,u_2,u_3),\mathbf{v}=(v_1,v_2,v_3)$
点积定义为：$\mathbf{u}\cdot \mathbf{v}=u_1{v}_1+u_2{v}_2+u_3{v}_3$

1.1.2 几何意义

点积也可以写成：$\mathbf{u}\cdot \mathbf{v}=\Vert \mathbf{u}\Vert \Vert \mathbf{v}\Vert cos\theta$
其中$\theta$是向量$u,v$之间的夹角。

• 如果$\theta <90^{\circ }：$点积$>0$
• 如果$\theta =90^{\circ }：$点积$=0$(正交)
• 如果$\theta >90^{\circ }：$点积<0

直观：点积 = 一个向量在另一个向量方向上的投影 × 另一个向量的长度。

1.1.3 主要应用

• 判断向量是否垂直（点积=0）
• 机器学习里：相似度度量（余弦相似度）

1.2 叉积（Cross Product）

1.2.1 定义（仅在三维空间有意义）

对于两个三维向量$\mathbf{u}=(u_1,u_2,u_3),\mathbf{v}=(v_1,v_2,v_3)$
叉积定义为：
$\mathbf{u}\times \mathbf{v}=\left|\begin{array}{ccc}\mathbf{i}& \mathbf{j}& \mathbf{k}\\ u_1& u_2& u_3\\ v_1& v_2& v_3\end{array}\right|=(u_2{v}_3-u_3{v}_2,u_3{v}_1-u_1{v}_3,u_1{v}_2-u_2{v}_1)$

1.2.2 几何意义

• 方向：$\mathbf{u}\times \mathbf{v}$垂直于$\mathbf{u}$和$\mathbf{v}$所在的平面（右手定则，四指并拢，拇指竖起，四指指向$\mathbf{u}$的方向，手掌旋转，从$\mathbf{u}$旋转到$\mathbf{v}$,拇指竖直指向叉积的方向。）
• 长度：$\Vert \mathbf{u}\times \mathbf{v}\Vert =\Vert \mathbf{u}\Vert \Vert \mathbf{v}\Vert sin\theta$，等于“以$\mathbf{u},\mathbf{v}$为边的平行四边形面积”。
  
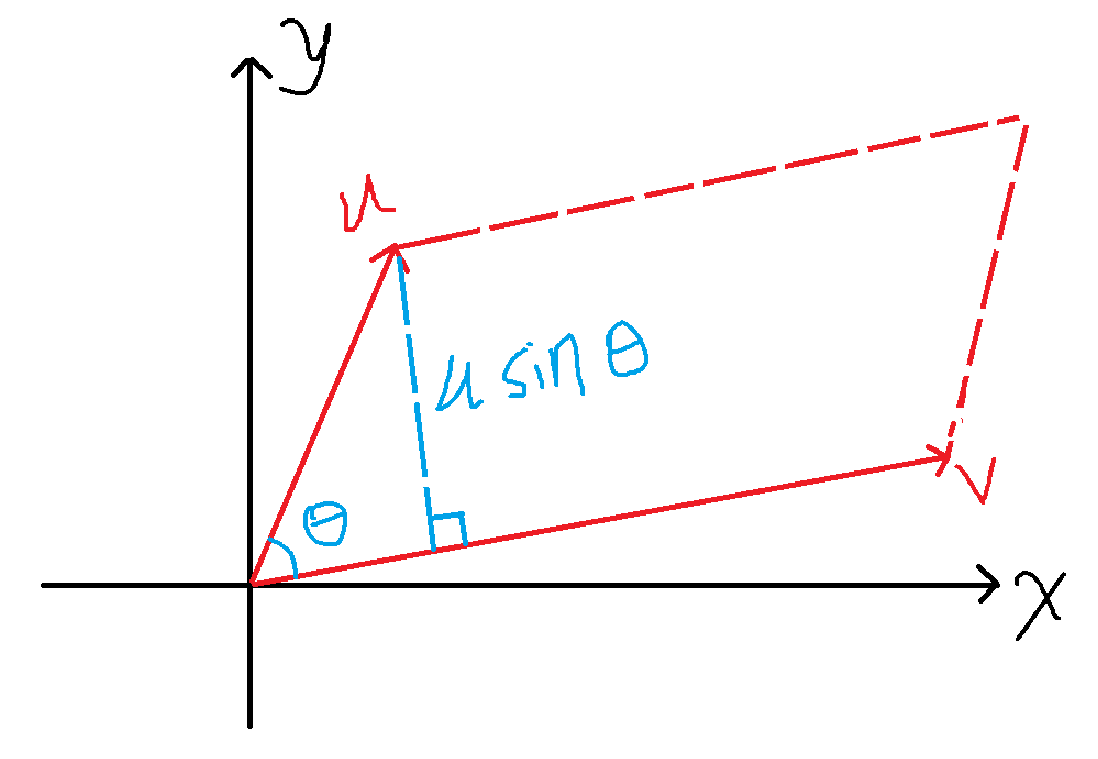
  直观：叉积 = 给出“垂直方向 + 面积大小”的向量。

1.2.3 主要应用

• 计算面积：$|\mathbf{u}\times \mathbf{v}|=$平行四边形面积
• 计算体积：$|\mathbf{u}\cdot (\mathbf{v}\times \mathbf{w})|=$平行六面体体积

1.3 向量减法

1.3.1 定义

给定两个向量：
$\mathbf{a}=(a_1,a_2,\cdots ,a_n)，\mathbf{b}=(b_1,b_2,\cdots ,b_n)$
它们的差定义为：
$\mathbf{a}-\mathbf{b}=(a_1-b_1,a_2-b_2,\cdots ,a_n-b_n)$
逐分量相减。

1.3.2 几何意义

在平面/空间里，$\mathbf{a}-\mathbf{b}$ 表示从 点 b 指向点 a 的向量。

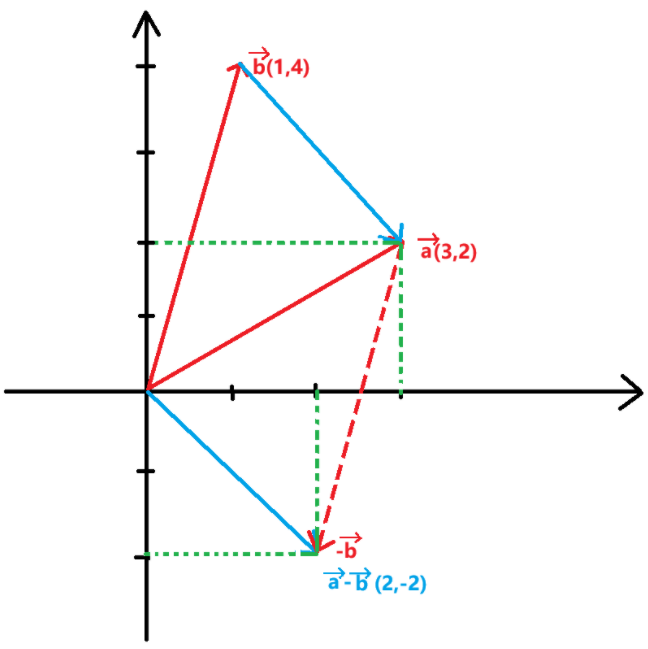
例子
在二维中：
$\mathbf{a}=(3,2)，\mathbf{b}=(1,4)$
则：$\mathbf{a}-\mathbf{b}=(3-1,2-4)=(2,-2)$
几何上，这就是从点 (1,4) 指向点 (3,2) 的向量。

1.4 向量加法

1.4.1 定义

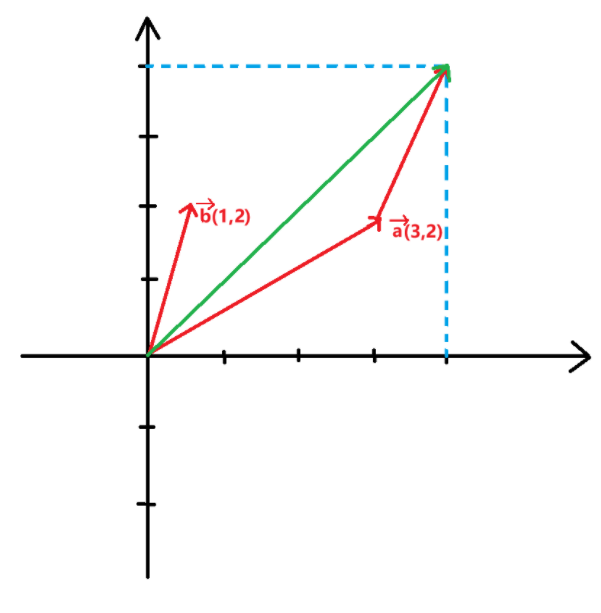
1.4.2

2.矩阵

2.1 基础内容

1.矩阵映射
$A:{\mathbb{R}}^p\to {\mathbb{R}}^m$代表矩阵$A$是$m\times p$，它接受一个$p$维的向量，输出一个$m$维的向量，也可表示为：$A\in {\mathbb{R}}^{m\times p}$
输入所需向量数为矩阵列数，输出向量数为矩阵行数。
2.各类表示
$det(A)：$矩阵$A$的行列式（只有方阵，即接受的向量和输出的向量数一致。）
$rank(A)：$矩阵$A$的秩

2.1 矩阵行列式

2.1.1 从二维出发（面积）

考虑二维矩阵：$A=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]$
它把单位正方形的两个基向量：$e_1=\left[\begin{array}{c}1\\ 0\end{array}\right],e_2=\left[\begin{array}{c}0\\ 1\end{array}\right]$
变换为：$A{e}_1=\left[\begin{array}{c}a\\ c\end{array}\right],A{e}_2=\left[\begin{array}{c}b\\ d\end{array}\right]$
所以正方形变成了一个平行四边形，它的面积是：$Area=|ad-bc|$，也就是$A{e}_1，A{e}_2$两个向量做叉积的绝对值，即$Area=|A{e}_1\times A{e}_2|$
这正好是$|det(A)|,A$的行列式的绝对值。
在二维，行列式就是单位正方形被矩阵变换后的面积缩放因子。

2.1.2 三维情况（体积）

三维矩阵：$A=\left[\begin{array}{ccc}a& b& c\\ d& e& f\\ g& h& i\end{array}\right]$
把单位立方体的三个基向量映射到新的三个向量：$v_1=(a,d,g{)}^T,v_2=(b,e,h{)}^T,v_3=(c,f,i{)}^T$
这三个向量张成一个平行六面体，它的体积由三重积给出：
$V=|v_1\cdot (v_2\times v_3)|=|(a,d,g)\cdot ((b,e,h)\times (c,f,i))|$
这个结果恰好就是$|det(A)|$

证明：
$v_2\times v_3=\left[\begin{array}{ccc}\mathbf{i}& \mathbf{j}& \mathbf{k}\\ b& e& h\\ c& f& i\end{array}\right]=(ei-hf,hc-bi,bf-ec)$
$$\begin{gathered} v_1\cdot (v_2\times v_3)=a(ei-hf)+d(hc-bi)+g(bf-ec) \\ =aei-ahf+dhc-dbi+gbf-gec \\ =a(ei-hf)-b(di-fg)+c(dh-eg) \end{gathered}$$
$\therefore |v_1\cdot (v_2\times v_3)|=|det(A)|$
在三维，行列式就是体积的伸缩因子。

$V=v_2\times v_3$，其中$V$的长度为$v_2，v_3$两个向量组成的平行四边形面积，这在叉积中有图作说明，而$V$的方向垂直于$v_2，v_3$所构成的平面。
$v_1\cdot V=|v_1||V|cos\theta ，|v_1|cos\theta$代表在向量$V$上的投影，即可看作以$v_2,v_3$构成平面为底的平行六面体的高，而|V|代表$v_2,v_3$为底的平行六面体的底面积。
故$|v_1\cdot (v_2\times v_3)|$为该平行六面体相对于三个基向量构成的基六面体变换的体积大小。

2.1.3 高维情况（推广）

在n维空间里，矩阵A把单位立方体（体积=1）映射到一个平行多面体。
行列式的绝对值$|det(A)|$就是这个新多面体的体积。
这是由行列式的代数性质决定的：
1.行列式在列向量线性相关时为 0（体积=0，空间被压扁，下一节细讲）；
2.行列式在交换两列时变号（体积方向翻转）；
证明：
$$\begin{gathered} A=\left[\begin{array}{ccc}a& b& c\\ d& e& f\\ g& h& i\end{array}\right]det(A)=a(ei-fh)-b(di-fg)+c(dh-eg) \\ B=\left[\begin{array}{ccc}a& b& c\\ g& h& i\\ d& e& f\end{array}\right]det(B)=a(fh-ei)-b(fg-di)+c(eg-dh)=-det(A) \end{gathered}$$
3.行列式在一列乘以常数时，结果也乘以这个常数（体积缩放）。
证明：
$$\begin{gathered} A=\left[\begin{array}{ccc}a& b& c\\ d& e& f\\ g& h& i\end{array}\right]det(A)=a(ei-fh)-b(di-fg)+c(dh-eg) \\ B=\left[\begin{array}{ccc}a& b& c\\ kd& ke& kf\\ g& h& i\end{array}\right] \\ det(B)=a(kei-kfh)-b(kdi-kfg)+c(kdh-keg) \\ =ka(ei-fh)-kb(di-fg)+kc(dh-eg)=kdet(A) \end{gathered}$$
这些正好与体积的几何性质一致，于是行列式就是“体积缩放因子”的唯一合理定义。

只有方阵有行列式。
行列式$det(A)$的本质作用是：

• 代数上：判断一个方阵是否可逆（$det(A)\ne 0\iff$可逆。
• 几何上：描述线性变换对应的提及缩放因子（带方向）。

这些性质都要求“输入空间维数 = 输出空间维数”，也就是：
$A：{\mathbb{R}}^n\to {\mathbb{R}}^n$
$\to$这只有在 𝐴 是方阵时才成立。
如果是非方阵，比如$3\times 4:$
$A：{\mathbb{R}}^4\to {\mathbb{R}}^3$

• 它把四维压到三维，体积一定被压成 0
• 没有“体积缩放”这个说法
• 所以行列式就没有定义

2.2 线性相关与线性无关

2.2.1 定义

设有一组向量$v_1,v_2,\cdots ,v_k$(在同一个向量空间里)
如果存在一组不全为零的系数$a_1,a_2,\cdots ,a_k$，使得$a_1{v}_1+a_2{v}_2+\cdots +a_k{v}_k=0$
那么这组向量就叫做 线性相关。
否则（只有当所有系数都等于 0 时，上式才成立），就叫做 线性无关。

2.2.2 几何直观

二维空间

• 如果两个向量在同一条直线上（共线），它们线性相关。
• 如果不共线，就线性无关。

三维空间

• 三个向量如果在同一个平面里（共面），它们线性相关。
• 如果能撑起整个三维空间，就线性无关。

一句话：一个向量可以由其它向量“拼出来”（线性组合），那它们就是相关的。

2.2.3 代数上的判定

把向量作为矩阵的列：$A=\left[\begin{array}{cccc}{v}_1& v_2& \cdots & v_k\end{array}\right]$

• 如果$det(A)=0$(方阵情况)，说明列向量线性相关
• 一般情况：秩$rank(A)<$列数$\to$列向量线性相关

秩$rank(A)<$列数的话对应$det(A)=0$，证明：
$A=\left[\begin{array}{ccc}a& b& c\\ d& e& f\\ a+2d& b+2e& c+2f\end{array}\right]$
这个$A$矩阵的列数就小于秩数，及
$$A=\left[\begin{array}{ccc}a& b& c\\ d& e& f\\ a+2d& b+2e& c+2f\end{array}\right]\to A=\left[\begin{array}{ccc}a& b& c\\ d& e& f\\ 0& 0& 0\end{array}\right]$$
$$\begin{gathered} det(A)=a(e(c+2f)-f(b+2e))-b(d(c+2f)-f(a+2d))+c(d(b+2e)-e(a+2d)) \\ =aec+2aef-afb-2afe-bdc-2bdf+bfa+2bfd+cdb+2cde-cea-2ced \\ =0 \end{gathered}$$

$det(A)=0$的几何体积说明：
$det(A)=0$说明在对应几维的空间里，体积为0。一般用每行代表特定维度（如第一行代表x轴），有多少行就有多少个维度。而有多少列说明有多少个向量。
比如如果两个二维列向量组成的矩阵$A$它的行列式$det(A)=0$，就说明其中一个列向量可以用另一个列向量表示出来。这两个列向量组成的平行四边形面积为0（面积相当于二维中的体积。）；
三个三维列向量组成的矩阵$B$它的行列式$det(B)=0$，就说明至少其中一个列向量可以用其他两个列向量表示出来，这三个列向量组成的三维体积为0（但二维面积并不一定为0。）；
类似的可以推广至四维，行列式为0，四维体积一定为0，但三维体积却不一定。因此有可以使用降维的方式获取线性不相关的向量，在机器学习中，或者叫获取线性不相关的特征。

2.2.4 线性相关和线性无关为什么重要？

• 线性无关的向量：可以当作“基底”，张成一个空间。
• 线性相关的向量：含有冗余信息，多余的那个能被其它的表示。

在机器学习/数据分析中:

• 如果特征（变量）线性相关，就会出现多重共线性问题 → 回归系数不稳定。
• 在 PCA（主成分分析）中，我们寻找线性无关的方向来表示数据。

总结：
线性相关 = 存在冗余，一个向量能用其它的拼出来。
线性无关 = 没冗余，它们是“独立的方向”，能作为基底。

2.3 矩阵的秩

2.3.1 定义

对于一个矩阵$A$，它的秩定义为：
$rank(A)$=列空间的维数=行空间的维数
常用同义表述：

• $rank(A)$ = 「最多能选出多少个线性无关的列向量」
• $rank(A)$ = 「最多能选出多少个线性无关的行向量」
• 对方阵：$rank(A)=n\iff A$可逆 $\iff det(A)\ne 0\iff$ 列/行向量线性无关 $\iff$ 特征值$\ne 0\iff$所有特征值非零。

2.3.2 列空间/行空间是什么？

• 列向量$Col(A)$：$A$ 的所有列向量的线性组合集合，位于 $R^m$ 中。 维数 = $rank(A)$。
• 行空间 $Row(A)$：$A$ 的所有行向量的线性组合集合，位于 $R^n$ 中。维数 = $rank(A)$。

直观地说：列空间就是 $Ax$ 能到达的所有输出方向；行空间是 $A^{t}y$ 能到达的所有方向。

2.3.3 秩的计算

最常用：行变换到行最简形（RREF）
变换到行最简形后就知道选出最大多少线性无关的行向量数，即秩的数量。

• 用初等行变换把 A 化为 RREF，数主元个数即为 rank(A)。
• 行变换不会改变秩。

小例子（行简化）：
$$\begin{gathered} A=\left[\begin{array}{ccc}1& 2& 3\\ 2& 3& 1\\ 4& 7& 7\end{array}\right] \\ ①R2\leftarrow R2-2R1A=\left[\begin{array}{ccc}1& 2& 3\\ 0& -1& 5\\ 4& 7& 7\end{array}\right] \\ ②R3\leftarrow R3-4R1A=\left[\begin{array}{ccc}1& 2& 3\\ 0& -1& 5\\ 0& -1& 5\end{array}\right] \\ R2\leftarrow R2-2R1A=\left[\begin{array}{ccc}1& 2& 3\\ 0& -1& 5\\ 0& 0& 0\end{array}\right] \end{gathered}$$
$\therefore rank(A)=2$

2.3.4 常用不等式与不变性

1.$rank(AB)\le min(rank(A),rank(B))$

2.4 可逆与不可逆

2.4.1 可逆的定义

矩阵 𝐴 可逆（invertible），是指：存在一个矩阵 $A^{-1}$，使得 $A{A}^{-1}=A^{-1}A=I$
其中 𝐼 是单位矩阵。

• 如果存在这样的逆矩阵，称 可逆矩阵。
• 如果不存在这样的逆矩阵，称 不可逆矩阵（奇异矩阵 singular matrix）。

可逆矩阵一定是方阵，证明：
如果$A$是$m\times n$，$A^{-1}$是$n\times m$，则$A{A}^{-1}$为$m\times m$，$A^{-1}A$为$n\times n$。$A{A}^{-1}\ne A^{-1}A$

2.4.2 代数意义

可逆矩阵：
线性方程组 $Ax=b$ 有唯一解 $x$。

不可逆矩阵：
线性方程组 $Ax=b$ 没有解 或 有无穷多个解。
特别地，$Ax=0$ 的唯一解不再是 $x=0$，还可能有非零解（这就是“非零解”的来源）。

为啥可逆矩阵有唯一解？不可逆矩阵没有解或者无穷多个解？
1.假设$A$为可逆矩阵，$A\in {\mathbb{R}}^{n\times n}$，$x\in {\mathbb{R}}^{n\times 1}$，$A$可以和$x$列出$n$个方程，方程的右边等于$b$，$n$个方程解$x$的$n$个未知数，确定唯一解。
2.假设$A$为不可逆矩阵，$A\in {\mathbb{R}}^{n\times n}$，$x\in {\mathbb{R}}^{n\times 1}$，$rank(A)<n$。

在方程少于$n$个时，又分为两种情况。
①$b$属于$A$的列空间。
②$b$不属于$A$的列空间。