马尔科夫链（Markov Chain）是一种经典的随机过程模型，因俄国数学家安德烈・马尔科夫（Andrey Markov）而得名。它的核心特点是 “无后效性”—— 未来状态的概率仅取决于当前状态，与过去的状态无关。这种特性使其在预测、决策、随机模拟等领域具有广泛应用，是数学建模中解决 “动态随机问题” 的重要工具。​

马尔科夫链广泛应用于诸如人口迁移、用户行为预测、气象模拟、文本生成、设备寿命分析等离散状态建模场景中，尤其适用于状态数量有限、状态转移具有统计规律的建模问题。

一、马尔可夫链的定义

要理解马尔科夫链，需先明确三个核心概念：状态空间、转移概率和无后效性，这三者共同构成了模型的理论基石。

1. 状态与状态空间

状态：系统在某一时刻的 “处境” 或 “特征”，用离散的符号表示。例如：​
天气模型中，状态可定义为 “晴（S₁）、阴（S₂）、雨（S₃）”；​
股票走势中，状态可定义为 “上涨（S₁）、持平（S₂）、下跌（S₃）”。​
状态空间（记为 I）：所有可能状态的集合，通常是有限离散集合，即 $I=S_1,S_2,...,S_n$（n 为状态总数）。

2. 无后效性（马尔科夫性）​

这是马尔科夫链的核心性质，用概率语言可严格表述为：​

这是马尔科夫链的核心性质，用概率语言可严格表述为：​
对于任意时刻 $t_1<t_2<...<t_k<t$，以及任意状态，有：
$P(X_t=S_m\mid X_{t_k}=S_j,X_{t_{k-1}}=S_{i_{k-1}},...,X_{t_1}=S_{i_1})=P(X_t=S_m\mid X_{t_k}=S_j)$

通俗理解：只要知道系统 “现在” 的状态，就能预测 “未来”，无需关心 “过去” 是如何到达当前状态的。例如，预测明天的天气，只需知道今天的天气，无需知道昨天或上周的天气。

3. 转移概率与转移概率矩阵

（1）一步转移概率

设系统在时刻 t 处于状态 $S_i$，在时刻 t+1 转移到状态 $S_j$的概率，称为一步转移概率，记为：
​$p_{ij}=P(X_{t+1}=S_j\mid X_t=S_i)(i,j=1,2,...,n)$

其满足两个基本性质：​

1. 非负性：$p_{ij}\ge 0$（概率不可能为负）；​
2. 行和为 1：${\sum }_{j=1}^n{p}_{ij}=1$（从状态 $S_i$ 出发，必然转移到某个状态）。

假设连续记录 10 天天气，状态序列如下（数字对应状态）：​
第 1 天：1（晴）、第 2 天：1（晴）、第 3 天：2（阴）、第 4 天：2（阴）、第 5 天：1（晴）、​第 6 天：1（晴）、第 7 天：1（晴）、第 8 天：2（阴）、第 9 天：1（晴）、第 10 天：1（晴）

一步转移描述 “当日状态→次日状态”，10 天数据对应9 个转移对（从第 1→2 天到第 9→10 天），手动列出所有转移对：​
第 1→2 天：1→1（晴→晴）​
第 2→3 天：1→2（晴→阴）​
第 3→4 天：2→2（阴→阴）​
第 4→5 天：2→1（阴→晴）​
第 5→6 天：1→1（晴→晴）​
第 6→7 天：1→1（晴→晴）​
第 7→8 天：1→2（晴→阴）​
第 8→9 天：2→1（阴→晴）​
第 9→10 天：1→1（晴→晴）

按 “初始状态（当日）” 分类，统计转移到 “目标状态（次日）” 的次数（记为$i$= 初始状态，​$j$= 目标状态），手动计数即可：

1. 初始状态为$S_1$（晴天）的转移次数

先筛选 “初始状态 = 1” 的转移对：共 6 个（第 1、2、5、6、7、9 对），再统计目标状态：​

• 1→1（晴→晴）：第 1、5、6、9 对 → 4 次
• 1→2（晴→阴）：第 2、7 对 → 2 次

从$S_1$出发的总转移次数：4+2=6 次（与筛选出的转移对数量一致，计数正确）

2. 初始状态为$S_2$（阴天）的转移次数

初始状态为$S_2$筛选 “初始状态 = 2” 的转移对：共 3 个（第 3、4、8 对），统计目标状态：​

• 2→1（阴→晴）：第 4、8 对 → 2 次​
• 2→2（阴→阴）：第 3 对 → 1 次​

从$S_2$出发的总转移次数：2+1=3 次（与筛选出的转移对数量一致，计数正确）

整理转移次数表

初始状态 \ 目标状态	$S_1$（晴）	$S_2$（晴）
​$S_1$（晴）	4	2
$S_2$（晴）	2	1

验证总转移次数：6+3=9 次（与 10 天数据对应 9 个转移对完全匹配，无计数错误）。​

根据定义，一步转移概率$p_{ij}=\frac{\text{从}{S}_i\text{到}{S}_j\text{的转移次数}}{\text{从}{S}_i\text{出发的总转移次数}}$,

$p_{11}$（晴→晴）： $\frac{4}{6}\approx 0.667$

$p_{12}$（晴→阴）：$\frac{2}{6}\approx 0.333$

$p_{21}$（阴→晴）： $\frac{2}{3}\approx 0.667$

$p_{22}$（阴→阴）：$\frac{1}{3}\approx 0.333$

验证概率性质

非负性：所有$p_{i}j$（0.667、0.333、0.667、0.333）均≥0，符合要求；

行和为 1：​

第 1 行（晴）：0.667+0.333=1
第 2 行（阴）：0.667+0.333=1

（2）转移概率矩阵

将所有一步转移概率按行（当前状态）和列（下一状态）排列，得到一步转移概率矩阵，记为

$P=\left(\begin{array}{cccc}{p}_{11}& p_{12}& ...& p_{1n}\\ p_{21}& p_{22}& ...& p_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ p_{n1}& p_{n2}& ...& p_{nn}\end{array}\right)$

例如，天气模型（3 个状态：晴 S₁、阴 S₂）的转移矩阵可能为：

$P=\left(\begin{array}{cc}{p}_{11}& p_{12}\\ p_{21}& p_{22}\end{array}\right)=\left(\begin{array}{cc}\frac{2}{3}& \frac{1}{3}\\ \frac{2}{3}& \frac{1}{3}\end{array}\right)$

（3）k 步转移概率矩阵​

若要预测 “k 步后” 的状态（如后天的天气，即 2 步转移），需用到k 步转移概率矩阵，记为 $P^{(k)}$
。根据 “Chapman-Kolmogorov 方程”，k 步转移矩阵可由一步转移矩阵的 k 次幂得到：$P^{(k)}=P^k$

例如，2 步转移矩阵 $P^{(2)}=P\times P$，其元素 $p_{ij}^{(2)}$ 表示 “从状态 $S_i$出发，经过 2 步转移到 $S_j$ 的概率”。

二、马尔科夫链的关键性质（平稳性与遍历性）​

在数学建模中，我们常关注 “长期稳定状态”，这需要通过马尔科夫链的平稳性和遍历性来分析。​

2.1 平稳分布（极限分布）

若存在一个概率向量 $\pi =({\pi }_1,{\pi }_2,...,{\pi }_n)$ （满足 ${\pi }_j\ge 0$且 ${\sum }_{j=1}^n{\pi }_j=1$ ），使得：$\pi =\pi P$

则称 $\pi$ 为马尔科夫链的平稳分布。​

通俗理解：当系统达到平稳分布时，状态的概率分布不再随时间变化。例如，长期观察天气后发现，晴、阴、雨的概率稳定在（0.3, 0.4, 0.3），此时无论初始天气如何，最终都会趋近于这个分布。

2.2 遍历性​

若马尔科夫链满足：​

1. 从任意初始状态出发，经过足够多步后，能到达所有状态（即 “不可约”）；​
2. 不存在 “周期性循环”（即 “非周期”）；

则称该马尔科夫链具有遍历性，且满足：${\lim }_{k\to \infty }{P}^{(k)}=\left(\begin{array}{cccc}{\pi }_1& {\pi }_2& ...& {\pi }_n\\ {\pi }_1& {\pi }_2& ...& {\pi }_n\\ ⋮& ⋮& \ddots & ⋮\\ {\pi }_1& {\pi }_2& ...& {\pi }_n\end{array}\right)$

即 k 步转移矩阵的所有行都趋近于平稳分布 $\pi$。这意味着：无论初始状态如何，长期后系统的状态分布都会收敛到平稳分布—— 这是马尔科夫链用于 “长期预测” 的核心依据。​

三、马尔科夫链模型的建模步骤（附实例）​

以 “预测某地区未来天气分布” 为例，完整建模流程如下：​
步骤 1：确定状态空间​
根据问题定义离散状态。此处定义：

状态 1（S₁）：晴天；​
状态 2（S₂）：阴天；​
状态 3（S₃）：雨天；​
状态空间 $S_1,S_2,S_3$

步骤 2：收集数据，估计转移概率矩阵​
通过历史数据（如过去 30 天的天气记录）计算转移频率，近似作为转移概率。例如，

假设研究者连续记录 30 天天气，得到如下状态序列（数字 1 = 晴天、2 = 阴天、3 = 雨天）：​
第 1 天：1（晴）、第 2 天：1（晴）、第 3 天：1（晴）、第 4 天：2（阴）、第 5 天：2（阴）、​
第 6 天：1（晴）、第 7 天：3（雨）、第 8 天：3（雨）、第 9 天：1（晴）、第 10 天：1（晴）、​
第 11 天：1（晴）、第 12 天：1（晴）、第 13 天：1（晴）、第 14 天：1（晴）、第 15 天：2（阴）、​
第 16 天：2（阴）、第 17 天：3（雨）、第 18 天：1（晴）、第 19 天：1（晴）、第 20 天：1（晴）、​
第 21 天：2（阴）、第 22 天：1（晴）、第 23 天：3（雨）、第 24 天：3（雨）、第 25 天：3（雨）、​
第 26 天：2（阴）、第 27 天：2（阴）、第 28 天：2（阴）、第 29 天：3（雨）、第 30 天：3（雨）

统计得：

• 晴天（S₁）后：18 次转晴天、9 次转阴天、3 次转雨天 → 频率（0.6, 0.3, 0.1）→ 转移概率 $p_{11}=0.6,p_{12}=0.3,p_{13}=0.1$；​
• 阴天（S₂）后：6 次转晴天、15 次转阴天、9 次转雨天 → 频率（0.2, 0.5, 0.3）→ 转移概率$p_{21}=0.2,p_{22}=0.5,p_{23}=0.3$ ；​
• 雨天（S₃）后：3 次转晴天、12 次转阴天、15 次转雨天 → 频率（0.1, 0.4, 0.5）→ 转移概率 $p_{31}=0.1,p_{32}=0.4,p_{33}=0.5$

​
最终得到转移矩阵 $P=\left(\begin{array}{ccc}0.6& 0.3& 0.1\\ 0.2& 0.5& 0.3\\ 0.1& 0.4& 0.5\end{array}\right)$

步骤 3：分析模型的遍历性（验证长期预测可行性）​

需验证两点：​
不可约性：从任意状态出发能到达所有状态。例如，S₁→S₂→S₃→S₁，存在路径，故不可约；​
非周期性：不存在正整数 d>1，使得所有转移步数都是 d 的倍数。例如，从 S₁出发，1 步可回 S₁（d 不整除 1），故非周期；​
因此，该马尔科夫链具有遍历性，可求平稳分布。

步骤 4：求解平稳分布（长期预测）​

根据平稳分布定义 $\pi =\pi P$，结合${\pi }_1+{\pi }_2+{\pi }_3=1$，建立方程组：

$\{\begin{array}{l}{\pi }_1=0.6{\pi }_1+0.2{\pi }_2+0.1{\pi }_3\\ {\pi }_2=0.3{\pi }_1+0.5{\pi }_2+0.4{\pi }_3\\ {\pi }_3=0.1{\pi }_1+0.3{\pi }_2+0.5{\pi }_3\\ {\pi }_1+{\pi }_2+{\pi }_3=1\end{array}$

解方程组得：$\pi =(0.25,0.4,0.35)$

步骤 5：短期预测（利用 k 步转移矩阵）​

若今天是晴天（初始状态向量 ${\pi }^{(0)}=(1,0,0)$，预测明天（1 步后）和后天（2 步后）的天气分布：​

• 明天（1 步）：${\pi }^{(1)}={\pi }^{(0)}P=(1\tilde{A}—0.6+0\tilde{A}—0.2+0\tilde{A}—0.1,...)=(0.6,0.3,0.1)$
• 后天（2 步）：${\pi }^{(2)}={\pi }^{(1)}P=(0.6\tilde{A}—0.6+0.3\tilde{A}—0.2+0.1\tilde{A}—0.1,...)=(0.43,0.35,0.22)$

即后天晴天概率 43%，阴天 35%，雨天 22%。​

四、马尔科夫链的常见应用场景​

应用马尔可夫链的计算方法进行马尔可夫分析，主要目的是根据某些变量现在的情况及其变动趋向，来预测它在未来某特定区间可能产生的变动，作为提供某种决策的依据。

除天气预测外，马尔科夫链在数学建模中还有大量应用，核心是 “状态离散、无后效性” 的问题：

• 经济领域：股票走势预测（状态：涨 / 平 / 跌）、市场占有率预测（状态：各品牌）；
• 生物领域：种群状态转移（状态：健康 / 患病 / 死亡）、DNA 序列分析；
• 工程领域：设备故障预测（状态：正常 / 维修 / 故障）、交通流量控制（状态：畅通 / 拥堵）；
• 社会领域：人口迁移预测（状态：农村 / 城市）、用户行为分析（状态：活跃 / 沉睡）。

五、建模注意事项​

1. 状态定义需合理：状态需离散、互斥，且能完整描述系统（如天气若加 “多云”，需补充为 4 状态）；​
2. 转移概率需可靠：尽量用足够多的历史数据估计，避免主观赋值；若数据不足，可结合专家经验修正；​
3. 遍历性验证不可少：若模型不满足遍历性（如存在 “吸收态”，如 “死亡” 状态无法转移），则无平稳分布，需调整模型（如定义 “吸收马尔科夫链”）。

六、常见扩展模型

高阶马尔科夫链：引入更多历史状态影响

隐马尔科夫模型 HMM：用于观测数据不可直接看到状态的情形（如语音识别）

马尔科夫决策过程 MDP：引入“动作”和“奖励”，用于强化学习建模

七：代码

python版

import numpy as np
import matplotlib.pyplot as plt# 原始天气状态序列：1=晴（sunny），2=阴（cloudy），3=雨（rainy）
weather_seq = [1, 1, 1, 2, 2, 1, 3, 3, 1, 1, 1, 1, 1, 1,2, 2, 3, 1, 1, 1, 2, 1, 3, 3, 3, 2, 2, 2, 3, 3]n_states = 3  # 3种状态：sunny(1)、cloudy(2)、rainy(3)
count_matrix = np.zeros((n_states, n_states))  # 初始化转移计数矩阵# 构建转移计数矩阵（统计从当前状态到下一状态的次数）
for i in range(len(weather_seq) - 1):current = weather_seq[i] - 1  # 状态索引从0开始（对应原1/2/3）next_ = weather_seq[i + 1] - 1count_matrix[current, next_] += 1# 归一化为转移概率矩阵 P（每行和为1，满足概率性质）
P = count_matrix / count_matrix.sum(axis=1, keepdims=True)
print("State Transition Probability Matrix P：\n", np.round(P, 3))  # 输出概率矩阵（保留3位小数）# 初始状态（已知第1天是晴天：Day1 is sunny）
pi_0 = np.zeros(n_states)
pi_0[weather_seq[0] - 1] = 1  # 初始状态向量：晴天概率=1，其他为0# 生成30天的状态分布（马尔科夫链演化：Markov Chain Evolution）
def simulate_markov(P, pi_0, steps=30):history = [pi_0]  # 存储每天的状态概率分布pi = pi_0.copy()  # 当前状态分布for _ in range(steps):pi = pi @ P  # 矩阵乘法：计算下一天的状态分布history.append(pi)return np.array(history)  # 返回31天的分布（初始+30天）history = simulate_markov(P, pi_0, steps=30)  # 执行模拟# 输出前5天结果示意（Show first 5 days for demonstration）
print("\nFirst 5 Days' State Distribution:")
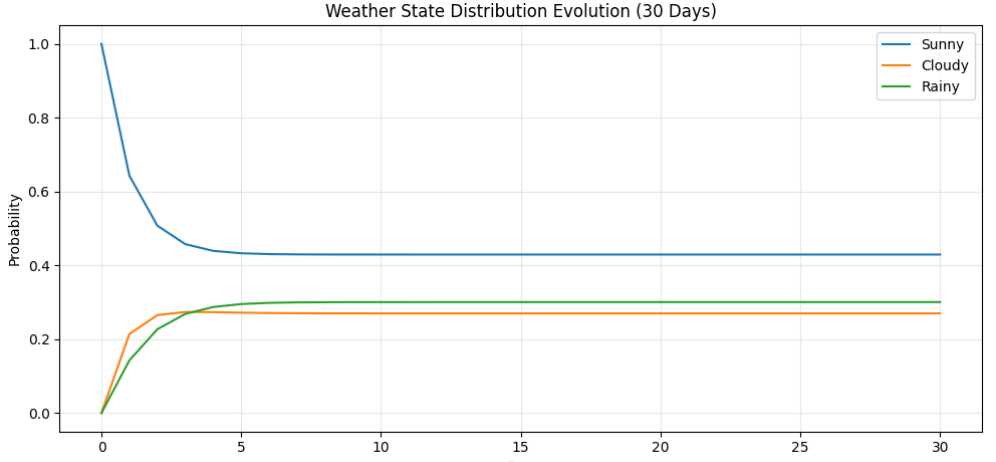
for i in range(5):print(f"Day {i}: Sunny={history[i][0]:.3f}, Cloudy={history[i][1]:.3f}, Rainy={history[i][2]:.3f}")# 可视化：天气状态分布演化（Visualization: Weather State Distribution Evolution）
plt.figure(figsize=(10, 5))  # 设置图大小
plt.plot(history[:, 0], label="Sunny")  # 晴天概率曲线
plt.plot(history[:, 1], label="Cloudy")  # 阴天概率曲线
plt.plot(history[:, 2], label="Rainy")  # 雨天概率曲线
plt.title("Weather State Distribution Evolution (30 Days)")  # 图标题
plt.xlabel("Day")  # x轴标签（天数）
plt.ylabel("Probability")  # y轴标签（概率）
plt.xticks(np.arange(0, 31, 5))  # x轴刻度：每5天显示1个
plt.grid(True, alpha=0.3)  # 显示网格（透明度0.3，避免遮挡曲线）
plt.legend(loc="best")  # 图例：自动放在最佳位置
plt.tight_layout()  # 自动调整布局，避免标签被截断
plt.show()  # 显示图像

输出结果：

State Transition Probability Matrix P：[[0.643 0.214 0.143][0.25  0.5   0.25 ][0.286 0.143 0.571]]First 5 Days' State Distribution:
Day 0: Sunny=1.000, Cloudy=0.000, Rainy=0.000
Day 1: Sunny=0.643, Cloudy=0.214, Rainy=0.143
Day 2: Sunny=0.508, Cloudy=0.265, Rainy=0.227
Day 3: Sunny=0.458, Cloudy=0.274, Rainy=0.269
Day 4: Sunny=0.439, Cloudy=0.273, Rainy=0.287

matlab版

% 原始天气序列（1=晴，2=阴，3=雨）
weather_seq = [1 1 1 2 2 1 3 3 1 1 1 1 1 1 ...2 2 3 1 1 1 2 1 3 3 3 2 2 2 3 3];n_states = 3;
count_matrix = zeros(n_states);% 构建转移计数矩阵
for i = 1:(length(weather_seq) - 1)current = weather_seq(i);next = weather_seq(i+1);count_matrix(current, next) = count_matrix(current, next) + 1;
end% 转移概率矩阵 P
P = count_matrix ./ sum(count_matrix, 2);
disp('状态转移概率矩阵 P:');
disp(round(P, 3));% 初始状态分布（Day 1 是“晴”）
pi_0 = zeros(1, n_states);
pi_0(weather_seq(1)) = 1;% 演化30天
steps = 30;
pi_t = zeros(steps+1, n_states);
pi_t(1, :) = pi_0;
for t = 2:(steps+1)pi_t(t, :) = pi_t(t-1, :) * P;
enddisp('前5天状态分布：');
disp(round(pi_t(1:5, :), 3));% 可视化（如需要）
figure;
plot(0:steps, pi_t(:, 1), '-o', 'DisplayName', '晴 (sunny)');
hold on;
plot(0:steps, pi_t(:, 2), '-o', 'DisplayName', '阴 (cloudy)');
plot(0:steps, pi_t(:, 3), '-o', 'DisplayName', '雨 (rainy)');
xlabel('天数');
ylabel('概率');
title('天气状态分布演化（30天）');
legend;
grid on;