软件构建（拓扑排序）

题目描述：

某个大型软件项目的构建系统拥有 N 个文件，文件编号从 0 到 N - 1，在这些文件中，某些文件依赖于其他文件的内容，这意味着如果文件 A 依赖于文件 B，则必须在处理文件 A 之前处理文件 B （0 <= A, B <= N - 1）。请编写一个算法，用于确定文件处理的顺序。

输入描述：

第一行输入两个正整数 N, M。表示 N 个文件之间拥有 M 条依赖关系。

后续 M 行，每行两个正整数 S 和 T，表示 T 文件依赖于 S 文件。

输出描述：

输出共一行，如果能处理成功，则输出文件顺序，用空格隔开。

如果不能成功处理（相互依赖），则输出 -1。

输入示例：

5 4
0 1
0 2
1 3
2 4

输出示例：

0 1 2 3 4

提示信息：

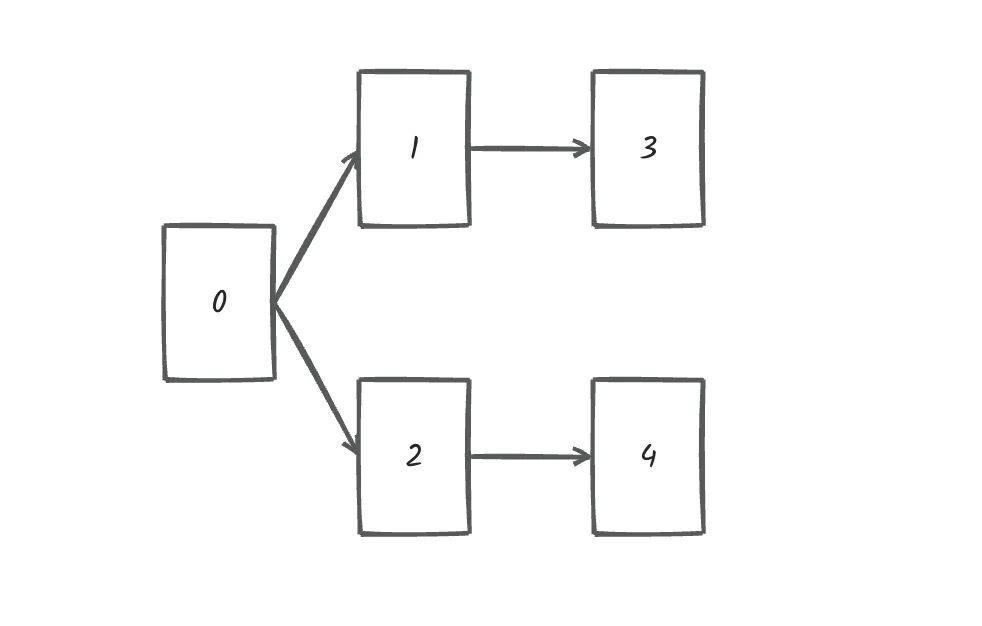
文件依赖关系如下：

所以，文件处理的顺序除了示例中的顺序，还存在

0 2 4 1 3

0 2 1 3 4

等等合法的顺序。

数据范围：

0 <= N <= 10 ^ 5

1 <= M <= 10 ^ 9

每行末尾无空格。

思路：

其实就两步：

1.找到入度为0的节点，加入结果集；

2.将该节点从图中移除。

用本题给出的示例来模拟这一过程：

1.找到入度为0的节点0，加入结果集：

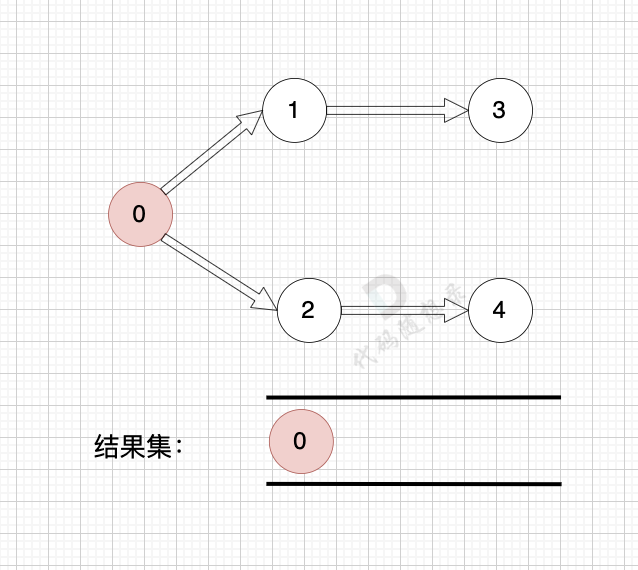
2.将该节点从图中移除：

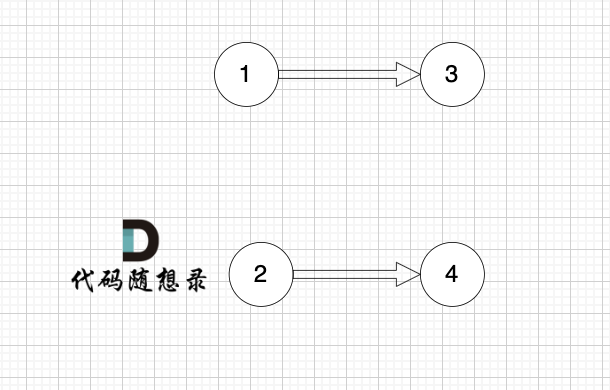
3.找到入度为0的节点1，加入结果集：（注意这里选1或者选2都可以）

4.将节点1从图中移除：

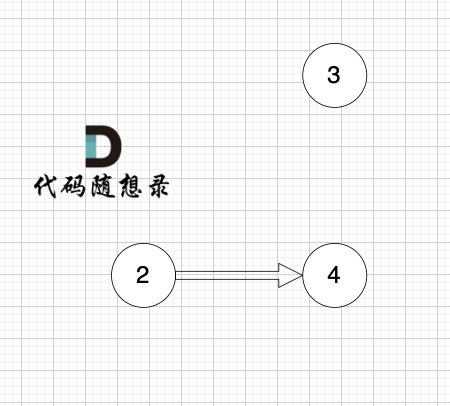
之后的过程以此类推。

知道了过程，代码就好写了：

import java.util.*;public class Main{private static List<List<Integer>> list=new ArrayList<>();public static void main(String[] args){Scanner in=new Scanner(System.in);int n=in.nextInt();int m=in.nextInt();for(int i=0;i<n;i++){list.add(new ArrayList<>());}int[] indegree=new int[n];for(int i=0;i<m;i++){int u=in.nextInt();int v=in.nextInt();indegree[v]++;list.get(u).add(v);}Queue<Integer> q=new LinkedList<>();for(int i=0;i<n;i++){if(indegree[i]==0)q.offer(i);}List<Integer> res=new ArrayList<>();while(!q.isEmpty()){int cur=q.poll();res.add(cur);for(Integer node:list.get(cur)){indegree[node]--;if(indegree[node]==0)q.offer(node);}}if(res.size()!=n){System.out.println(-1);return;}for(int i=0;i<res.size()-1;i++){System.out.print(res.get(i)+" ");}System.out.print(res.get(res.size()-1));}
}

参加科学大会（dijkstra算法朴素版）

【题目描述】

小明是一位科学家，他需要参加一场重要的国际科学大会，以展示自己的最新研究成果。

小明的起点是第一个车站，终点是最后一个车站。然而，途中的各个车站之间的道路状况、交通拥堵程度以及可能的自然因素（如天气变化）等不同，这些因素都会影响每条路径的通行时间。

小明希望能选择一条花费时间最少的路线，以确保他能够尽快到达目的地。

【输入描述】

第一行包含两个正整数，第一个正整数 N 表示一共有 N 个公共汽车站，第二个正整数 M 表示有 M 条公路。

接下来为 M 行，每行包括三个整数，S、E 和 V，代表了从 S 车站可以单向直达 E 车站，并且需要花费 V 单位的时间。

【输出描述】

输出一个整数，代表小明从起点到终点所花费的最小时间。

输入示例

7 9
1 2 1
1 3 4
2 3 2
2 4 5
3 4 2
4 5 3
2 6 4
5 7 4
6 7 9

输出示例

12

提示信息

能够到达的情况：

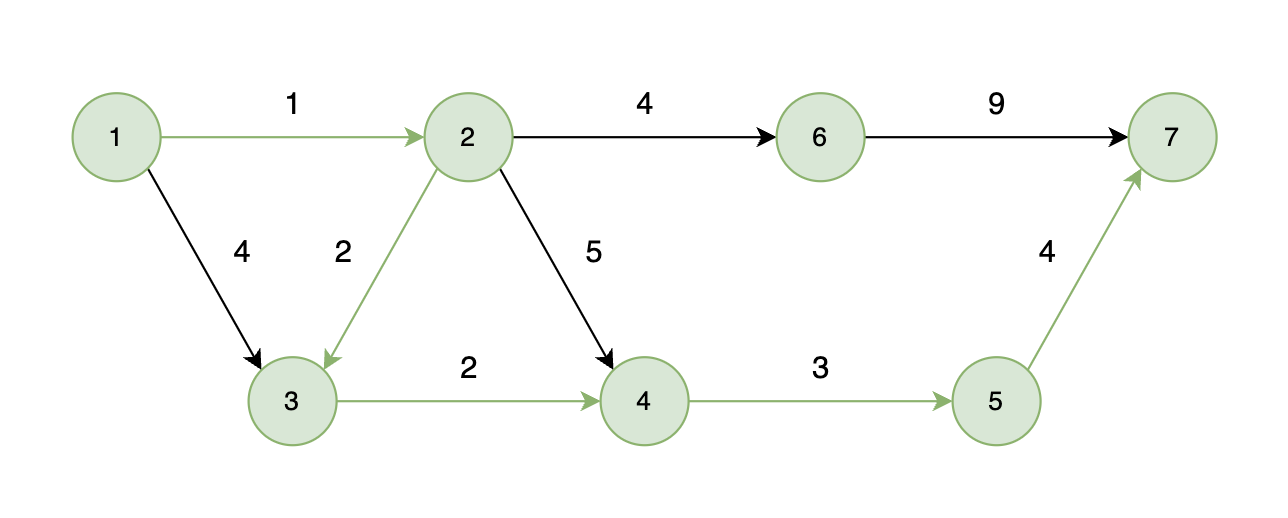
如下图所示，起始车站为 1 号车站，终点车站为 7 号车站，绿色路线为最短的路线，路线总长度为 12，则输出 12。

不能到达的情况：

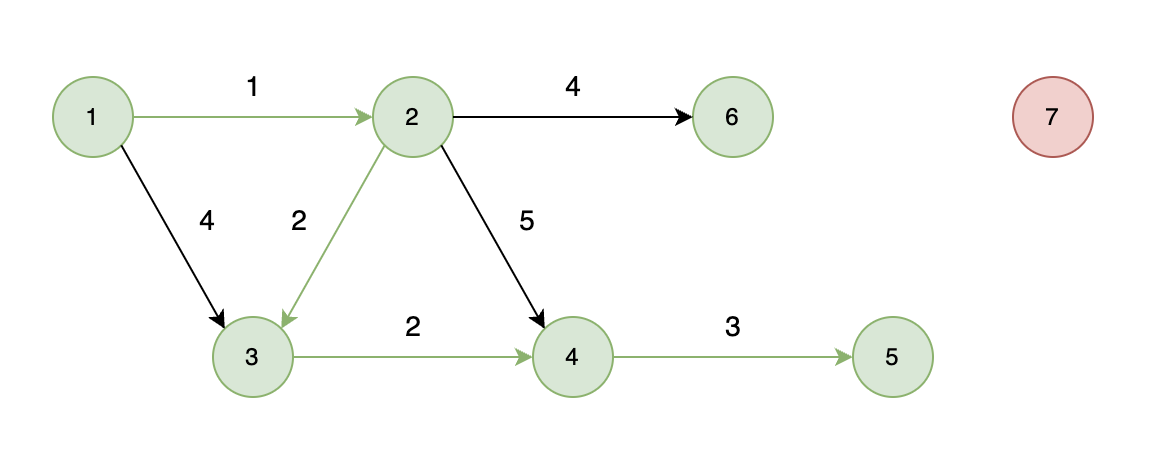
如下图所示，当从起始车站不能到达终点车站时，则输出 -1。

数据范围：

1 <= N <= 500;
1 <= M <= 5000;

dijkstra算法步骤：

1.选源点到哪个节点近且该节点未被访问过；

2.该最近节点被标记访问过；

3.更新非访问节点到源点的距离（也就是minDist数组）。

其实和prim算法是和相似的，只不过prim算法是在不形成环的情况下判断访问每一个节点需要的最小花费；而dijkstra算法不一定需要访问每一个节点，它求的是源节点到其他节点的最小花费，不需要考虑成环这种情况。所以在代码上会有差异。（prim算法的代码见我的上一篇文章）

这是prim算法更新minDist数组的写法：

for (int j = 1; j <= v; j++) {if (!isInTree[j] && grid[cur][j] < minDist[j]) {minDist[j] = grid[cur][j];}
}

这是dijkstra算法更新minDist数组的写法：

for (int v = 1; v <= n; v++) {if (!visited[v] && grid[cur][v] != INT_MAX && minDist[cur] + grid[cur][v] < minDist[v]) {minDist[v] = minDist[cur] + grid[cur][v];}
}

完整代码如下：

import java.util.*;public class Main{public static void main(String[] args){Scanner in=new Scanner(System.in);int n=in.nextInt();int[] minDist=new int[n+1];minDist[1]=0;for(int i=2;i<=n;i++)minDist[i]=Integer.MAX_VALUE;boolean[] visited=new boolean[n+1];int m=in.nextInt();int[][] graph=new int[n+1][n+1];for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){graph[i][j]=Integer.MAX_VALUE;}}for(int i=0;i<m;i++){int s=in.nextInt();int e=in.nextInt();int v=in.nextInt();graph[s][e]=v;}for(int i=1;i<=n;i++){int Min=Integer.MAX_VALUE;int cur=1;for(int j=1;j<=n;j++){if(visited[j]==false&&minDist[j]<Min){Min=minDist[j];cur=j;}}visited[cur]=true;for(int j=1;j<=n;j++){if(visited[j]==false&&graph[cur][j]!=Integer.MAX_VALUE&&Min+graph[cur][j]<minDist[j]){minDist[j]=Min+graph[cur][j];}}}if(minDist[n]!=Integer.MAX_VALUE)System.out.println(minDist[n]);else System.out.println(-1);}
}