一、分析赛题核心意义

收集近 11 年的赛题并非简单的 “题目存档”，而是为了从历史规律、能力匹配、实战准备三个维度为参赛者或研究者提供价值。

1.1把握竞赛命题趋势，降低选题盲目性

赛题命题往往紧扣当年社会热点、科技前沿与行业痛点（如 2024 年 E 题 “交通流量管控” 对应城市旅游拥堵治理，2021 年 A 题 “FAST 主动反射面调节” 关联国家重大科技工程）。通过纵向梳理，可清晰发现命题从 “纯理论建模” 向 “实际问题解决” 倾斜（如近年赛题普遍增加 “数据预处理”“多约束优化” 要求），也能总结高频命题领域（如交通优化、生产决策、环境分析、科技工程类题目占比超 60%），帮助参赛者提前聚焦优势领域，避免临赛时因不熟悉题型而选错题目。

1.2构建 “问题 - 模型” 对应思维，提升建模效率

数学建模的核心是 “用合适的模型解决特定问题”，而历史赛题是 “问题与模型匹配” 的最佳案例库。例如：

遇到 “资源分配 / 成本优化” 类问题（如 2024 年 B 题生产决策、2020 年 C 题信贷决策），可关联 “线性规划 / 整数规划模型”；
遇到 “概率预测 / 风险评估” 类问题（如 2024 年 D 题深弹命中概率、2019 年 E 题薄利多销分析），可关联 “概率论 / 马尔可夫链模型”。

收集赛题能帮助使用者建立 “看到问题→联想对应模型” 的条件反射，减少建模初期的思路混乱。

1.3 积累实战数据与边界条件处理经验

赛题并非 “理想化数学题”，而是包含大量 “实际约束”（如 2023 年 E 题黄河水沙分析需处理 “数据缺失”，2022 年 D 题气象传输需考虑 “误码率限制”）。收集赛题时，可同步关注题目中 “隐含的边界条件”（如时间限制、成本上限、数据误差范围），这些细节是建模能否落地的关键 —— 而历史赛题的 “约束设置规律”（如工业类题目常含 “生产周期约束”，环境类题目常含 “自然变量波动约束”），能为后续实战提供参考，避免因忽略实际约束导致模型 “纸上谈兵”。

1.4 为团队分工与能力补全提供依据

数学建模需 3 人团队分工（建模、编程、写作），不同赛题对团队能力的要求差异显著：

科技工程类题目（如 2024 年 A 题板凳龙、2014 年 A 题嫦娥三号）需较强的 “物理建模 + 编程实现” 能力（如用 MATLAB 仿真运动轨迹）；
数据分析类题目（如 2023 年 C 题蔬菜定价、2018 年 C 题会员画像）需较强的 “数据处理 + 统计学” 能力（如用 Python 做回归分析）。

收集赛题后，可根据团队成员特长（如 “擅长编程者适合工业类题，擅长统计者适合数据分析类题”）提前规划分工，避免临赛时因能力不匹配导致效率低下。

年份	赛题	题目	简介
2024 年	A 题	“板凳龙” 闹元宵	需对动态系统建模，模拟舞龙队伍在螺旋路径中的行进过程，求解队伍每秒的位置、速度，进行碰撞检测与路径优化等
2024 年	B 题	生产过程中的决策问题	企业生产电子产品，需购买两种零配件进行装配。要为企业设计抽样检测零配件的方案，在已知零配件和成品次品率等情况下，对生产各阶段（零配件检测、成品检测、不合格成品处理、用户退回不合格品处理）作出决策；还要考虑多工序、多零配件的复杂生产过程的决策
2024 年	C 题	农作物的中值策略	需考虑农作物种植面积、成本、收益、作物间的替代性与互补性，以及价格、气候等不确定性因素，通过建立动态种植模型研究农作物种植的最优策略
2024 年	D 题	反潜航空深弹命中概率问题	基于反潜战术中的深弹投射场景，运用军事知识和概率论原理，对相关情况合理简化，构建数学模型计算深弹命中潜艇的概率
2024 年	E 题	交通流量管控	以小镇道路为例，聚焦城市交通拥堵问题，特别是黄金周期间旅游车流的应对，通过数据预处理和条件假设，构建数学模型寻求解决方案
2023 年	A 题	定日镜场的优化设计	围绕定日镜场，从光学、力学等多方面考虑，对定日镜的布局、角度等进行优化设计，以提高太阳能的收集和利用效率
2023 年	B 题	多波束测线问题	在多波束测量场景下，针对测线的规划、测量数据的处理和分析等方面展开研究，以实现更高效、准确的海洋测量
2023 年	C 题	蔬菜类商品的自动定价与补货决策	结合蔬菜市场的需求变化、成本波动等因素，建立数学模型实现蔬菜类商品的自动定价，并制定合理的补货决策，以平衡收益和库存成本
2023 年	D 题	圈养湖羊的空间利用率	从圈养湖羊的养殖环境出发，考虑湖羊的生长习性、活动空间需求等，对养殖场地的布局和利用进行优化，提高空间利用率
2023 年	E 题	黄河水沙监测数据分析	对黄河水沙监测所获得的数据进行深入分析，挖掘数据背后的规律，为黄河的治理、水资源利用和生态保护提供数据支持和决策依据
2022 年	A 题	波浪能最大输出功率设计	针对波浪能的特点，通过物理建模和数学计算，设计相关装置或系统，以实现波浪能的高效捕获和转化，获得最大输出功率
2022 年	B 题	无人机遂行编队飞行中的纯方位无源定位	研究无人机在编队飞行时，仅依靠方位信息进行无源定位的方法，涉及信号处理、空间几何计算等多方面知识，以实现无人机的精准定位和编队控制
2022 年	C 题	古代玻璃制品的成分分析与鉴别	运用化学分析、统计学等方法，对古代玻璃制品的成分数据进行处理和分析，建立鉴别模型，判断玻璃制品的产地、年代等信息
2022 年	D 题	气象报文信息卫星通信传输	考虑气象报文信息在卫星通信传输过程中的特点和问题，如数据量、传输速率、误码率等，优化传输方案，保障气象信息的准确、快速传输
2022 年	E 题	小批量物料的生产安排	针对小批量物料生产场景，综合考虑生产流程、成本、交货期等因素，制定合理的生产计划和调度方案，提高生产效率和经济效益
2021 年	A 题	“FAST” 主动反射面的形状调节	基于 “FAST”（中国天眼）主动反射面的工作原理和结构特点，通过建立数学模型，研究如何对反射面的形状进行精确调节，以实现更好的信号接收效果
2021 年	B 题	乙醇耦合制备 C4 烯烃	围绕乙醇耦合制备 C4 烯烃的化学工艺过程，考虑反应条件、原料转化率、产物选择性等因素，建立数学模型优化反应过程，提高生产效率和产品质量
2021 年	C 题	生产企业原材料的订购与运输	生产企业需要对原材料进行订购和运输，要综合考虑原材料价格波动、运输成本、库存成本、生产需求等因素，建立模型制定最优的订购与运输策略
2021 年	D 题	连铸切割的在线优化	在连铸生产过程中，针对铸坯的切割环节，考虑铸坯的质量、切割速度、切割损耗等因素，通过数学模型实现切割过程的在线优化，提高生产效益
2021 年	E 题	中药材的鉴别	利用化学、生物学、统计学等多学科知识，对中药材的特征数据进行分析处理，建立鉴别模型，实现对中药材真伪、品质的准确鉴别
2020 年	A 题	炉温曲线	研究在特定工艺要求下，炉温随时间的变化规律，通过建立数学模型优化炉温控制策略，以满足生产过程中对炉温的精确要求
2020 年	B 题	穿越沙漠	给定穿越沙漠的相关条件，如沙漠长度、车辆载油量、加油站位置等，建立数学模型规划最优的穿越方案，包括行车路线、加油策略等
2020 年	C 题	中小微企业的信贷决策	综合考虑中小微企业的财务状况、信用记录、市场环境等因素，建立数学模型为金融机构提供信贷决策依据，评估贷款风险和收益
2020 年	D 题	接触式轮廓仪的自动标注	针对接触式轮廓仪获取的数据，研究如何通过算法实现自动标注，提高数据处理效率和准确性，涉及图像处理、模式识别等技术
2020 年	E 题	校园供水系统智能管理	结合校园用水需求的变化规律、供水设备的运行成本等因素，建立数学模型实现校园供水系统的智能管理，优化供水方案，节约水资源和成本
2019 年	A 题	高压油管的压力控制	围绕高压油管内的压力变化情况，通过建立物理和数学模型，研究压力控制方法，确保高压油管在安全和高效的状态下工作
2019 年	B 题	“同心协力” 策略研究	探索团队合作中 “同心协力” 的策略问题，可能涉及到博弈论、协同优化等知识，通过建立模型分析不同策略下团队的表现和收益
2019 年	C 题	机场的出租车问题	针对机场出租车的调度、乘客等待时间、出租车运营效率等问题，综合考虑机场客流量、出租车数量、交通状况等因素，建立数学模型优化出租车运营方案
2019 年	D 题	空气质量数据的校准	对空气质量监测所获得的数据，考虑监测设备误差、环境因素干扰等情况，通过数学方法对数据进行校准处理，提高数据的准确性和可靠性
2019 年	E 题	“薄利多销” 分析	从经济学角度出发，研究商品价格、销量、成本和利润之间的关系，建立数学模型分析 “薄利多销” 策略在不同市场环境下的可行性和效果
2018 年	A 题	高温作业专用服装设计	结合高温作业环境的特点和人体生理需求，从材料选择、服装结构设计等方面建立数学模型，设计出更适合高温作业人员的专用服装
2018 年	B 题	智能 RGV 的动态调度策略	针对智能 RGV（轨道式自动导引车）在生产线上的作业情况，考虑任务分配、运行路径规划、设备等待时间等因素，建立数学模型制定动态调度策略，提高生产效率
2018 年	C 题	大型百货商场会员画像描绘	利用大数据分析技术和数学统计方法，对大型百货商场会员的消费行为、偏好等数据进行处理和分析，构建会员画像，为商场精准营销提供支持
2018 年	D 题	汽车总装线的配置问题	在汽车总装生产线上，综合考虑零部件供应、装配工艺、生产效率、成本等因素，建立数学模型对总装线的设备、人员、生产流程等进行优化配置
2017 年	A 题	CT 系统参数标定及成像	研究 CT 系统的工作原理，通过建立数学模型对 CT 系统的参数进行标定，并利用标定后的参数实现更准确的成像，提高 CT 检测的精度
2017 年	B 题	“拍照赚钱” 的任务定价	针对 “拍照赚钱” 这种众包任务平台的任务定价问题，考虑任务难度、地理位置、市场需求、参与者收益等因素，建立数学模型制定合理的任务定价策略
2017 年	C 题	颜色与物质浓度辨识	运用光学、化学和数学知识，研究颜色与物质浓度之间的关系，通过建立模型实现对物质浓度的准确辨识，可应用于化学分析、质量检测等领域
2017 年	D 题	巡检线路的排班	在巡检工作场景下，考虑巡检人员数量、工作时间限制、巡检地点分布、设备重要性等因素，建立数学模型制定合理的巡检线路排班计划，提高巡检效率和质量
2016 年	A 题	系泊系统的设计	围绕海洋工程中的系泊系统，考虑海洋环境因素（如风浪流）、船舶或海洋结构物的运动特性等，通过建立数学模型设计安全、可靠且经济的系泊系统
2016 年	B 题	小区开放对道路通行的影响	研究小区开放这一城市规划措施对周边道路通行能力、交通流量分布、居民出行时间等方面的影响，通过建立数学模型进行定量分析和评估
2016 年	C 题	电池剩余放电时间预测	利用电池的充放电特性、历史数据、当前状态等信息，建立数学模型对电池剩余放电时间进行准确预测，为电池管理和设备使用提供参考
2016 年	D 题	风电场运行状况分析及优化	针对风电场的运行情况，考虑风力资源的变化、风机的性能、设备维护成本等因素，建立数学模型分析风电场的运行效率，并提出优化策略提高发电效益
2015 年	A 题	太阳影子定位	根据太阳的位置和物体影子的变化规律，通过建立数学模型，利用影子长度和方向等信息确定物体的地理位置或时间等参数
2015 年	B 题	互联网 + 时代出租车的资源配置	在 “互联网 +” 背景下，考虑出租车市场的供需关系、乘客出行需求分布、车辆调度成本等因素，建立数学模型优化出租车资源配置，提高运营效率和服务质量
2015 年	C 题	月上柳梢头	题目可能围绕月亮与柳树在特定场景下的光学、几何关系展开，通过建立数学模型研究相关现象，如月亮在树梢位置的时间、角度等问题
2015 年	D 题	众筹筑屋规划方案设计	结合众筹的特点和筑屋的需求、成本、收益等因素，建立数学模型制定众筹筑屋的规划方案，包括资金筹集、房屋设计、利益分配等方面
2014 年	A 题	嫦娥三号软着陆轨道设计与控制策略	依据嫦娥三号的任务要求和月球的引力场等环境因素，建立数学模型设计软着陆轨道，并制定相应的控制策略，确保嫦娥三号安全、准确地软着陆在月球表面
2014 年	B 题	创意平板折叠桌	从平板折叠桌的功能需求、结构设计、材料选择等方面出发，建立数学模型进行优化设计，使折叠桌在满足使用功能的同时，具备更好的便携性和美观性
2014 年	C 题	生猪养殖场的经营管理	综合考虑生猪养殖过程中的饲料成本、市场价格波动、养殖规模、疾病防控等因素，建立数学模型为生猪养殖场制定经营管理策略，实现经济效益最大化
2014 年	D 题	储药柜的设计	根据储药的种类、数量、储存条件、取药便捷性等要求，建立数学模型对储药柜的结构、布局进行优化设计，提高储药效率和药品管理水平

二、总结归纳赛题核心事项

总结解决方法需围绕 “分类归纳→模型拆解→细节优化→实战复用” 展开，具体可分为 5 个步骤，确保总结内容 “可落地、可迁移”：

2.1 先按 “题目类型” 分类，建立 “问题 - 方法” 对应框架

第一步需打破 “按年份排序” 的惯性，按 “题目核心需求” 对赛题分类（避免按 “A/B/C/D 题” 标签分类，因每年标签对应的题型可能变化），建议分为 6 大类，每类对应典型方法：

题目类型	典型赛题案例（年份 + 题号）	核心解决方法（模型 / 工具）	关键注意事项
资源优化 / 决策类	2024B、2023C、2020C、2014C	线性规划 / 整数规划（Lingo/Excel Solver）、动态规划	需明确 “目标函数”（如 “成本最小”“收益最大”）和 “约束条件”（如产能、预算）
概率预测 / 风险评估类	2024D、2019E、2016C、2015A	概率论、马尔可夫链、蒙特卡洛模拟（Python/MATLAB）	需验证 “概率分布假设”（如是否符合正态分布），处理 “小概率事件”
动态系统 / 物理建模类	2024A、2023A、2022A、2014A	微分方程（如牛顿运动方程）、仿真工具（MATLAB/Simulink）	需简化 “物理模型”（如忽略次要变量），避免模型过于复杂无法求解
数据分析 / 模式识别类	2023E、2022C、2018C、2017C	回归分析、聚类算法（K-Means）、机器学习（如随机森林）	需处理 “异常数据”（如用箱线图剔除 outliers），验证模型拟合度（R²/MAE）
交通 / 路径优化类	2024E、2023B、2019C、2017D	图论（Dijkstra 算法）、遗传算法（解决复杂路径问题）	需考虑 “动态变量”（如交通流量实时变化、巡检人员工作时长限制）
工业过程 / 流程优化类	2022E、2021D、2020A、2018B	排队论（处理生产等待问题）、离散事件仿真（AnyLogic）	需匹配 “工业实际流程”（如连铸切割需考虑 “生产节拍”，RGV 调度需考虑 “设备切换时间”）

2.2 对每类题目拆解 “标准解决流程”，明确步骤分工

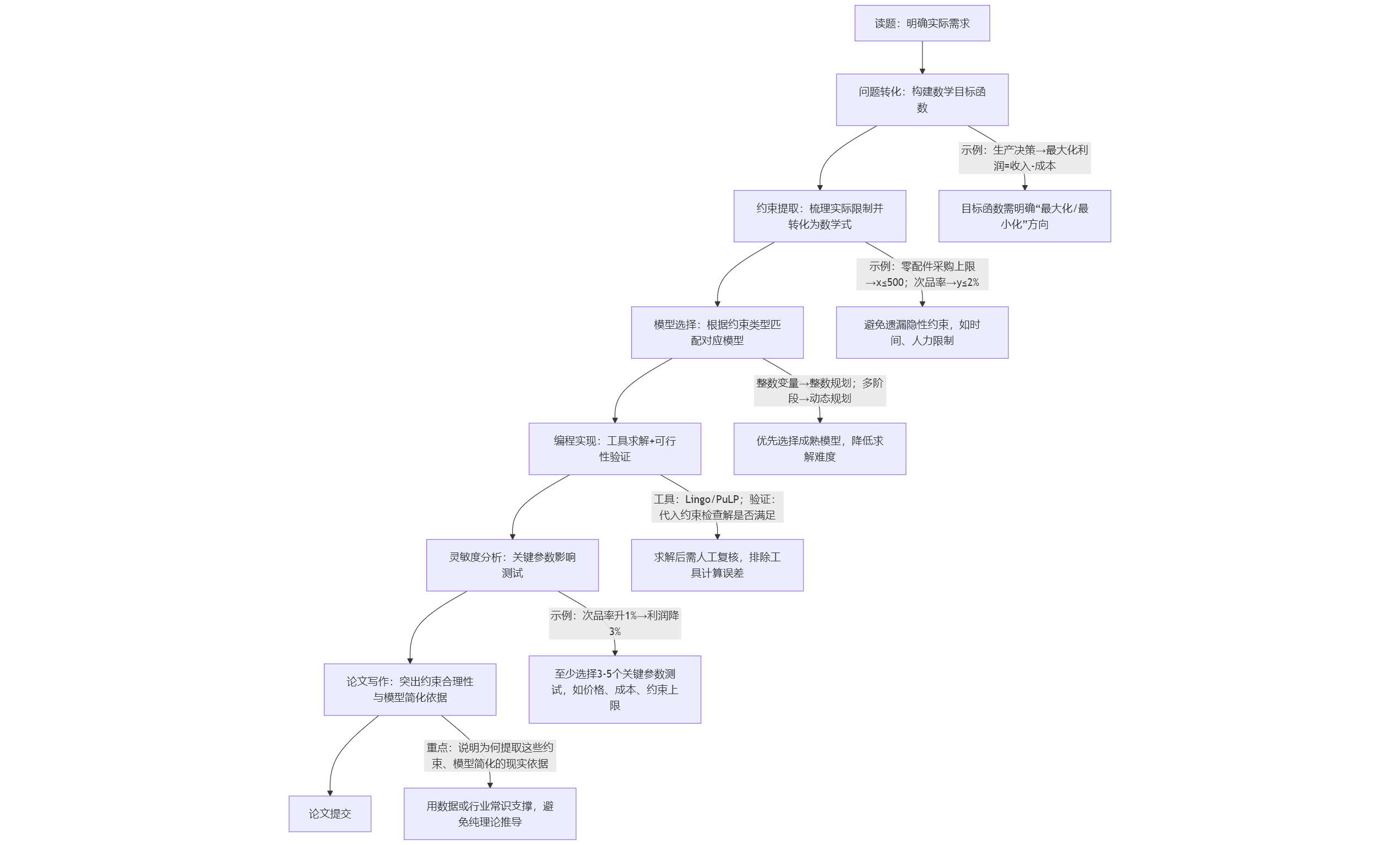
针对每类题目，总结 “从读题到论文提交” 的标准流程，避免实战时步骤混乱。以 “资源优化类题目” 为例，标准流程可拆解为：

问题转化：将题目中的 “实际需求” 转化为 “数学目标函数”（如 “生产决策”→“最大化利润 = 收入 - 成本”）；
约束提取：列出所有 “实际限制”（如零配件采购量上限、成品次品率限制），转化为 “数学不等式 / 等式”；
模型选择：根据约束类型选择模型（如 “整数变量”→整数规划，“多阶段决策”→动态规划）；
编程实现：用工具求解（如 Lingo 写规划方程，Python 用 PuLP 库求解），验证解的可行性（如是否满足所有约束）；
灵敏度分析：分析 “关键参数变化对结果的影响”（如 “零配件次品率上升 1%，利润下降多少”），增强模型鲁棒性；
论文写作：重点说明 “约束提取的合理性” 和 “模型简化的依据”（避免评委认为模型脱离实际）。

2.3 聚焦 “模型细节优化”，总结 “避坑点”

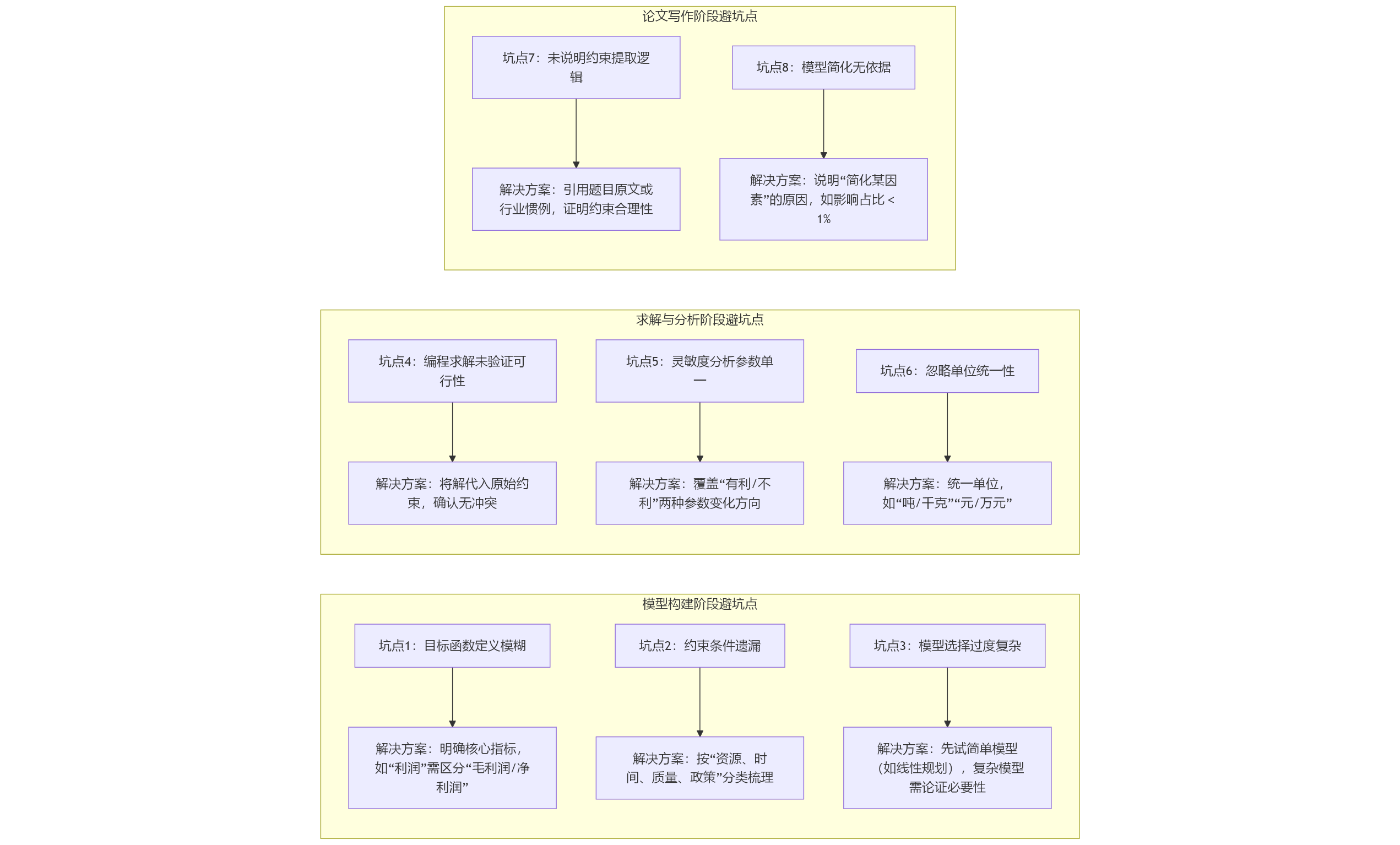
同一模型在不同赛题中的 “细节处理” 差异，是区分建模水平的关键。需总结每类模型的 “常见误区” 和 “优化技巧”，例如：

线性规划模型：若题目含 “模糊约束”（如 “成本尽可能低”），需补充 “模糊线性规划” 优化，避免用 “硬约束” 导致解不可行；
蒙特卡洛模拟：需注意 “抽样次数”（如 2024 年 D 题深弹命中概率，抽样次数过少会导致结果波动大，建议至少 10000 次）；
回归分析：若数据存在 “多重共线性”（如 2023 年 C 题蔬菜定价中 “销量与价格高度相关”），需用 “岭回归” 替代普通线性回归，避免系数估计偏差。
整理 “工具与代码模板”，提升实战效率

建模的核心是 “用工具实现思路”，而非重复编写基础代码。总结时可按 “模型类型” 整理工具和模板：

规划类模型：整理 Lingo/PuLP 的 “线性规划模板”（含目标函数、约束条件的固定语法）；
仿真类模型：整理 MATLAB 的 “动态系统仿真模板”（如运动轨迹仿真的微分方程求解代码）；
数据分析类模型：整理 Python 的 “数据预处理模板”（含缺失值填充、异常值剔除、特征工程的基础代码）。

模板需标注 “适用场景”（如 “此回归模板适用于‘销量 - 价格’线性关系分析”），避免盲目复用。

2.4. 结合 “优秀论文” 验证方法有效性，补充 “非模型因素”

赛题的 “解决方法” 不仅包括模型，还包括 “论文写作逻辑”“结果可视化” 等非模型因素 —— 这些是拿奖的关键。后续总结时，可结合全国一等奖论文（可从竞赛官网或高校建模协会获取）补充：

写作逻辑：优秀论文如何 “从实际问题切入→引出模型→验证结果→提出建议”（如 2023 年 E 题黄河水沙分析，优秀论文会先说明 “水沙数据的实际意义”，再讲模型，避免纯数学推导）；
结果可视化：如何用图表呈现复杂结果（如用热力图展示交通流量分布，用折线图展示利润随参数的变化）；
模型局限性与改进方向：优秀论文会主动说明 “模型的不足”（如 “未考虑极端天气对生产的影响”），并提出改进思路 —— 这能体现建模的严谨性，需纳入总结。

通过以上步骤，总结出的 “解决方法” 将不再是 “零散的模型列表”，而是 “从题目分类到实战落地” 的完整体系，既能帮助新手快速入门，也能为有经验的参赛者提供 “优化思路”，真正实现 “以史为鉴，提升实战能力”。