1. 题意

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

2. 题解

这个题不会做，全部是看得题解捏。

不过能看懂题解感觉自己也很棒了！

看完题解后感觉最难的是如何求出有多少积水，

答案直接给的是当前位置的积水量是它左右两边两个最大值的最小值

减去当前的高度。

灵茶山艾府的题解中解释了为什么？如果比两端最高的高积水肯定会

从一侧流出去。

不过我肯定是想不到的。

有了这个结论之后，其实就可以做一下了。

对于每个高度，求出它左右两侧的最高高度，从而计算积水的高度。

2.1 前后缀最大值

算出前后缀的最高高度。

再遍历一次计算积水量。

class Solution {
public:int trap(vector<int>& height) {int n = height.size();int ans = 0;vector<int> left_max(n, 0);vector<int> right_max(n, 0);for (int i = 1; i < n; ++i) {left_max[i] = max(left_max[i - 1], height[i - 1]);}for (int i = n - 2; ~i; --i) {right_max[i] = max(right_max[i + 1], height[i + 1]);}for (int i = 1; i < n - 1; ++i) {ans += max(0, min(left_max[i], right_max[i]) - height[i] );}return ans;}
};

当然可以稍微优化下空间，不过差别不大。

class Solution {
public:int trap(vector<int>& height) {int n = height.size();int ans = 0;vector<int> rightMx(n + 1, -1);for (int i = n - 1; ~i; --i) {rightMx[i] = max(height[i], rightMx[i + 1]);}int leftMx = height[0];for (int i = 1; i < n - 1; ++i) {ans += max( 0, min(leftMx, rightMx[i + 1]) - height[i]);leftMx = max(height[i], leftMx);}return ans;}
};

时间复杂度$O(n)$

空间复杂度$O(n)$

2.2 双指针

双指针的解法确实比较巧妙，先说下做法，再证明为什么正确，最后给出代码。

思路是，左指针$l$指向左端，右指针$r$指向右端，同时维护两个变量：

$leftMax$表示$l$左端的最大值，

$rightMax$表示$r$右端的最大值。

当$leftMax<rightMax$时，

左指针元素积水高度为$leftMax-height[l]$，左指针右移。

当$leftMax\ge rightMax$时，

右指针元素积水高度为$rightMax-height[r]$，右指针左移。

为什么这个策略正确呢? 下面简要证明。

我们令lmx(i)=max⁡{height[k],0≤k≤i}lmx(i) = \max\{height[k] , 0 \le k \le i\}lmx(i)=max{height[k],0≤k≤i}，

也就是$lmx(i)$表示下标$i$左端的最大值。

我们令rmx(i)=max⁡{height[k],i≤k≤n−1}rmx(i)=\max\{ height[k],i \le k \le n-1\}rmx(i)=max{height[k],i≤k≤n−1},

也就是$rmx(i)$表示下标$i$右端的最大值。

我们令$w[i]$表示位置$i$的积水高度，

那么$w[i]=\min (lmx(i),rmx(i))-height[i]$。

当$l\le r$时，我们很容易得到

$$\begin{gathered} lmx(l)\le lmx(r) \\ rmx(l)\ge rmx(r) \end{gathered}$$

上面的$leftMax$相当于$lmx(l)$，$rightMax$相当于$rmx(r)$。

当$lmx(l)<rmx(r)$时，必然有$lmx(l)<rmx(r)\le rmx(l)$，

因此$\min (lmx(l),rmx(l))=lmx(l)$。

同理$lmx(l)\ge rmx(r)$时，必然有$rmx(r)\le lmx(l)\le lmx(r)$，

因此$\min (lmx(r),rmx(r))=rmx(r)$。

综上，这个策略是正确的。

下面给出不那么重要的代码：

class Solution {
public:int trap(vector<int>& height) {int n = height.size();int ans = 0;int l = 0;int r = n - 1;int leftMax = 0;int rightMax = 0;while (l <= r) {leftMax = max( leftMax, height[l]);rightMax = max( rightMax, height[r]);if ( height[l] < height[r]) {ans += leftMax - height[l];++l;}else {ans += rightMax - height[r];--r;}}return ans;}
};

时间复杂度$O(n)$

空间复杂度$O(1)$

2.3 单调栈

说实话不是很明白单调栈的做法怎么想到的，

它比前后缀的做法要难理解的多，也不知道怎么来的，纯纯为了

用一下这个数据结构？

核心思想是逐步填充积水高度。

当栈顶元素大于新元素时，直接将新元素入栈。

否则，将栈顶元素出栈，令为$k$，

将积水高度填充到与新栈顶$left$或新元素$height[i]$的最小值，

即$\min (height[i],height[left])-height[k]$

填充的宽度就是$i-left-1$

不断重复这个过程直到栈空或者栈顶大于新元素，再将新元素入栈。

叙述起来很复杂，还是看下图吧，像个一步步填坑的过程。

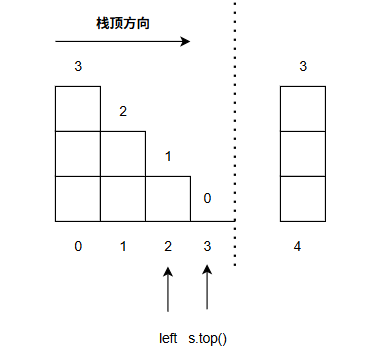
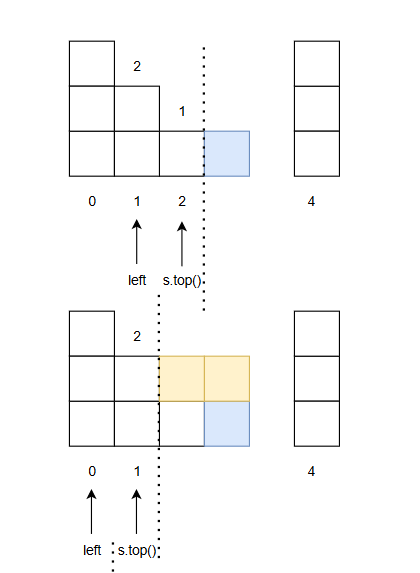
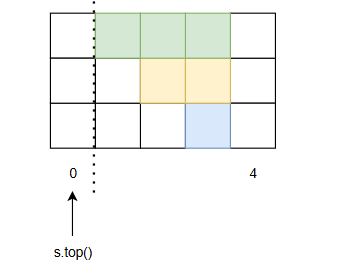
下面给出代码

class Solution {
public:int trap(vector<int>& height) {int n = height.size();stack<int> s;int ans = 0;for (int i = 0; i < n; ++i) { while (!s.empty() && height[s.top()] <= height[i]) {int k = s.top();s.pop();if (!s.empty()) {int left = s.top();ans += ( i - left - 1 ) * (min(height[i], height[left]) - height[k] );}}s.push( i );}return ans;}
};

时间复杂度$O(n)$，空间复杂度$O(n)$

3. 参考

leetcode
0x3f