题目描述

现给出一棵N个结点二叉树，问这棵二叉树中最长链的长度为多少，保证了1号结点为二叉树的根。

输入

第1行为包含了一个正整数N，为这棵二叉树的结点数，结点标号由1至N。
接下来N行，这N行中的第i行包含两个正整数l[i], r[i]，表示了结点i的左儿子与右儿子编号。如果l[i]为0，表示结点i没有左儿子，同样地，如果r[i]为0则表示没有右儿子。

输出

包括1个正整数，为这棵二叉树的最长链长度。

样例输入

样例输出

提示

样例解释
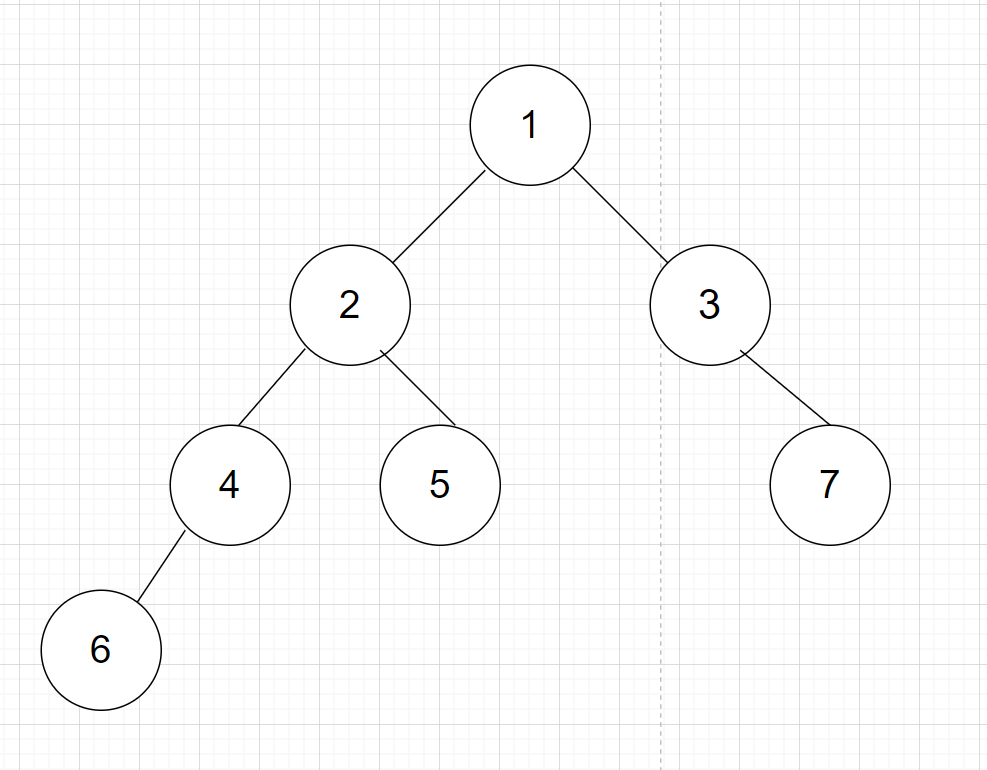
4-2-1-3-6为这棵二叉树中的一条最长链。

对于100%的数据，有N≤100000，且保证了树的深度不超过32768。

思路分析

使用深度优先搜索(DFS)计算每个节点的深度，然后遍历所有节点，计算通过每个节点的最长链（左右子树深度之和），取最大值作为结果。
二叉树的深度是指从根节点到叶子结点时，最多经过了几层。
在如上图所示的二叉树中，我们令：
节点5、6、7的深度为1；
节点3、4的深度为2；
节点2的深度是3；
节点1的深度是4。
采用深度优先搜索计算每个节点u的深度depth[u]。初始化depth数组N个元素的值为0。如果u=0，说明该节点不存在，直接返回。深搜节点u的左子节点和右子节点，节点u的深度为其左右子节点深度的最大值加一。
void dfs(int u){if(u==0)return;dfs(left_child[u]);dfs(right_child[u]);depth[u]=max(depth[left_child[u]],depth[right_child[u]])+1;
}
遍历n个节点（1-based indexing），计算通过该节点的最长链（即左子树深度+右子树深度），并更新最大值。
for(int i=1;i<=n;i++){int len=0;if(left_child[i]){len+=depth[left_child[i]];}if(right_child[i]){len+=depth[right_child[i]];}ans=max(ans,len);
}

代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e5+5;
int n,l,r,ans;
vector<int>left_child(N+1);
vector<int>right_child(N+1);
vector<int>depth(N+1,0);
void dfs(int u){if(u==0)return;dfs(left_child[u]);dfs(right_child[u]);depth[u]=max(depth[left_child[u]],depth[right_child[u]])+1;
}
int main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>n;for(int i=1;i<=n;i++){cin>>l>>r;left_child[i]=l;right_child[i]=r;}dfs(1);for(int i=1;i<=n;i++){int len=0;if(left_child[i]){len+=depth[left_child[i]];}if(right_child[i]){len+=depth[right_child[i]];}ans=max(ans,len);}cout<<ans;return 0;
}