排序

排序就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作

排序的稳定性

假若有以下数组，数组中存在两个5，这里区分标记

如果排序之后，红色的5仍然在蓝色的5前面，我们就认为该排序是稳定的

稳定

反之如果打乱了原本红色5在前的顺序，我们就认为该排序是不稳定的排序

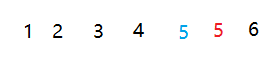 不稳定

常见的排序

插入排序

把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列。在生活中我们玩斗地主的时候，洗牌就是用到了插入排序。

具体流程如下

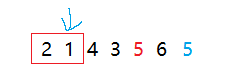第一个数据本身不用排序，从第二个数据开始，把前面两个数据看成一组，然后让1和该组的每一个元素进行比较如果找到合适的位置就插入

然后到第三个数据，这里发现已经有序则不进行改动

然后是第四个数据，一样的，把第四个数据和该组内的所有数据比较，然后找到合适的位置插入

后面也同理

对数组排序完成之后我们发现，插入排序是一种稳定的排序

插入排序的特性

1. 元素集合越接近有序，直接插入排序算法的时间效率越高

2. 时间复杂度：O(N^2)（此篇幅里说到时间复杂度代表平均复杂度）

3. 空间复杂度：O(1)

4. 稳定性：稳定

代码实现

 public static void insertSort(int[] array){for (int i = 1; i < array.length; i++) {int temp = array[i];int j = i-1;for (; j >= 0; j--) {if(array[j]>temp){array[j+1] =array[j];}else{break;}}array[j+1]=temp;}}

希尔排序

希尔排序法也叫做，缩小增量法。体现在排序当中就是对待排序列进行分组，每一组内分别排序，然后减少组数，直至减少到为一组，然后整体再进行排序，这样做的好处是，在缩小为一整组之前，带排序列的数据会基本趋近于有序的，这样就可以减小复杂度。

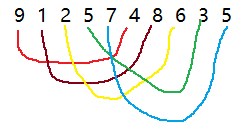这里有一组待排的数组，我们把数组分为五组，组内数据的间隔为5，然后进行分组排序。

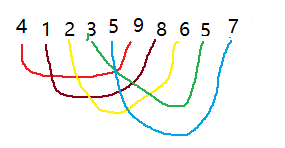
然后再分为两组，组内数据的间隔为2，然后再进行分组排序

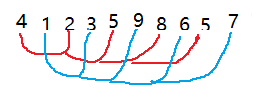
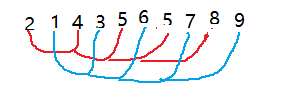
可以发现当分量缩小为2的时候，数组内的数据已经基本趋于有序了，这个时候再缩小增量，就是一整组进行排序

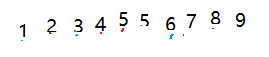
代码实现

 public static void shellSort(int[] array){int gap = array.length;while(gap>1){gap/=2;Shell(array,gap);}}private static void Shell(int[] array,int gap){for (int i = gap; i < array.length; i++) {int temp = array[i];int j = i-gap;for (; j >= 0; j-=gap) {if(array[j]>temp){array[j+gap] =array[j];}else{break;}}array[j+gap]=temp;}}

希尔排序的特性

1. 希尔排序是对直接插入排序的优化，当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序的了，这样就会很 快。这样整体而言，可以达到优化的效果。

2. 时间复杂度：

最好情况：O(N)

平均情况：O(N^1.3) 希尔排序的时间复杂度并不是稳定的，N的1.3次方是Knuth在进行大量的实验和测试得出了结论，所以我们认为希尔排序的时间复杂度是O(N^1.3)

最坏情况：O(N^2)

3. 空间复杂度：O(1)

4. 稳定性：不稳定

选择排序

每一次从待排序的数据元素中选出最小的一个元素，存放在序列的起始位置，放完之后，然后再从第二个元素开始找到后面最小的元素，以此循环，直到全部待排序的数据元素排完。

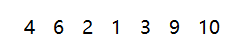
我们要对这组数据进行选择排序，先找第一个最小的数据，这里最小的数据为1，然后我们交换1 和 4

然后从第二个位置往后，再找最小的数据，最小数据为2，2 和 6交换

以此往复，得到结果

代码实现

这里的selectSort2是另一种选择排序的思路

 public static void selectSort(int[] array){for (int i = 0; i < array.length; i++) {int minIndex = i;for (int j = i+1; j < array.length; j++) {if(array[j]<array[minIndex]){minIndex = j;}}swap(array,i,minIndex);}}public static void selectSort2(int[] array){int left = 0 ;int right = array.length-1;while(left<right){int minIndex = left;int maxIndex = left;for (int i = left+1; i <=right; i++) {if(array[i]<array[minIndex]){minIndex = i;}if(array[i]>array[maxIndex]){maxIndex = i;}}swap(array,left,minIndex);if(maxIndex==left){maxIndex = minIndex;}swap(array,right,maxIndex);left++;right--;}}private static void swap(int[] array,int a,int b){int temp = array[a];array[a] = array[b];array[b] = temp;}

选择排序的特性

1. 直接选择排序思考非常好理解，但是效率不是很好，实际中很少使用

2. 时间复杂度：O(N^2)

3. 空间复杂度：O(1)

4. 稳定性：不稳定

堆排序

前面了解堆这种数据结构的时候提到过堆分为大根堆和小根堆，这里要说到的堆排序就是基于大根堆和小根堆的特性来实现的。如果要求数据从小到大排序就建立大根堆，反之小根堆。

流程为：将一组数据建堆，这里以从小到大的排序为目标，建立一个大根堆，然后把堆顶元素和最后的元素进行交换，交换完成之后对堆顶进行向下调整，然后缩小调整的范围，这样堆的最后一个元素就是最大的元素了。

这里画图举例，假若有一组数据为 1  6  2  4  10  9  3，对这组数据建立大根堆

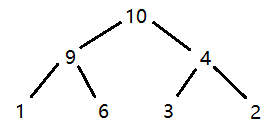
然后交换堆顶元素和数组的最后一个元素

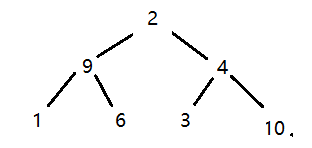
交换完成之后我们缩小调整的范围，这样10就不会受到后面调整的影响了，这里用红圈标起来

调整为大根堆

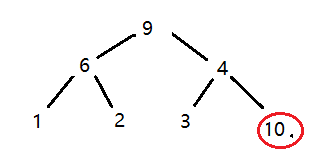
然后再交换堆顶元素和最后一个元素

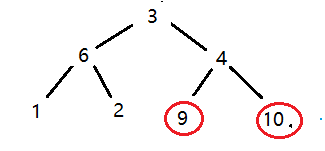
再对堆进行调整

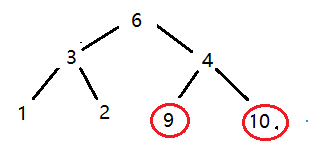
以此往复

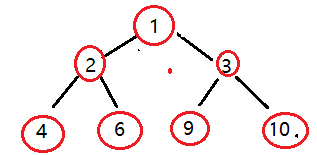
代码实现

public static void heapSort(int[] array){createBigHeap(array);int end = array.length-1;while(end>0){swap(array,0,end);siftDown(array,0,end);end--;}}private static void createBigHeap(int[] array){for(int parent = (array.length-1-1)/2;parent>=0;parent--){siftDown(array,parent,array.length);}}private static void siftDown(int[] array,int parent,int end){int child=parent*2+1;while(child<end){if(child+1<end&&array[child+1]>array[child]){child++;}if(array[child]>array[parent]){swap(array,child,parent);parent = child;child= parent*2 +1;}else{break;}}}

堆排序的特性

1. 堆排序使用堆来选数，效率就高了很多。

2. 时间复杂度：O(N*logN)

3. 空间复杂度：O(1)

4. 稳定性：不稳定

冒泡排序

冒泡排序很简单，这里不细细展开

代码实现

这里进行了一点优化，可以减小复杂度

 public static void bubbleSort(int[] array) {for (int i = 0; i < array.length; i++) {boolean flag = false;//标记for (int j = 0; j < array.length-i-1; j++) {if(array[j]>array[j+1]){swap(array,j+1,j);flag=true;//如果走不到这一步}}if(flag==false){//说明已经有序，则从这里退出方法return ;}}}

冒泡排序的特性

1. 冒泡排序是一种非常容易理解的排序

2. 时间复杂度：O(N^2)

3. 空间复杂度：O(1)

4. 稳定性：稳定

快速排序

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元 素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有 元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

快速排序的核心围绕着定基准来进行

先说说第一种方法：Hoare法

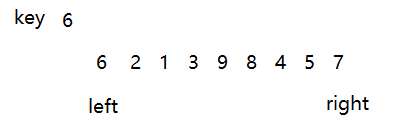
以第一个数据为基准，然后定义两个下标，先移动右下标，找到比key小的元素就停止，然后到左下标，移动左下标，找到比key大的元素就停止。

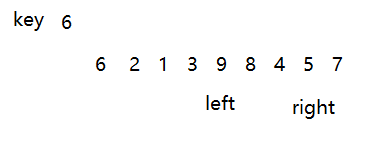
这里找到了9比6大，5比6小，然后交换两个元素。

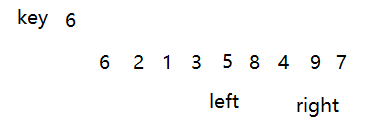
继续移动，先右再左，找到目标

然后交换，先移动右下标

当左右下标相遇时停止，让left或者right下标元素和最左边的元素交换

此时发现以6为基准，6的左边所有的元素都小于6，6右边的所有元素都大于6

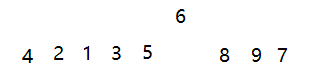
然后在把数组分为两个部分，左边的一组再以4为基准来定基准，右边的一组再以8为基准来定基准以此循环，最终达到排序的效果。

第二种方法：挖坑法

同样的顺序，先移动右边，遇到比key小的元素停下

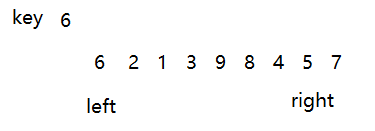
然后把5挖起来盖住左下标的位置

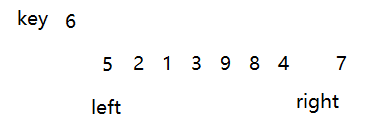
然后再移动左下标，找到比6大的元素

然后挖起来放到右下标的位置

然后右下标

然后左下标

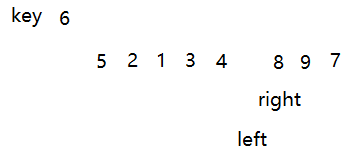
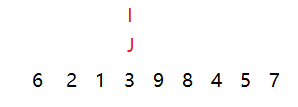
然后右下标

当左右下标相遇时，把key放入相遇的位置

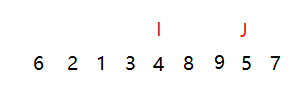
第三种方法：前后指针法

定义两个下标，

然后按照以下规则移动和交换

取左边下标为key，这里是6，如果J下标的元素小于key，移动I下标，如果I下标和J下标重合，则继续移动J下标，直至不满足条件位置，最后I下标和左边的元素交换即可。

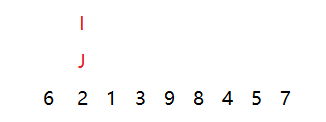
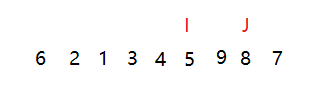
可以发现三种方法定基准的左右数据都把一样，这里更加推荐使用挖坑法进行定基准

代码实现

 private static int partition2(int[] array,int left ,int right) {//Hoare交换法求基准int key = array[left];//选left下标的数作为基准int i = left;//记录下左边下标while(left<right){while(left<right && array[right]>=key){//多加个判断防止越界right--;//没遇到比key小的就往前走}while(left<right && array[left]<=key){left++;//没遇到比key大的就往后走}swap(array,left,right);//遇到大的在前，小的再后，此时就可以交换两个下标的值}swap(array,i,right);//相遇之后交换基准和相遇的地方return left;//返回基准，这样就可以做到，调整顺序，和找基准}private static int partition(int[] array,int left ,int right) {//挖坑法int key = array[left];//选left下标的数作为基准while(left<right){while(left<right&&array[right]>key){right--;}array[left] = array[right];while(left<right&&array[left]<key){left++;}array[right] = array[left];}array[left]=key;return left;//挖坑法的优先度更高，因为会省去交换的操作，从而达到减小复杂度的效果}private static int partition3(int[] array,int left,int right){//前后指针法int front = left;int rear = left +1;while(rear<=right){if(array[rear]<array[left]&&array[++front]!=array[rear]){swap(array,rear,front);}rear++;}swap(array,front,left) ;return front;}

这里有一种特殊的情况，如果一组数据为 1 2 3 4 5 6 7  这样有序或者趋于有序的数据，此时还将左边的第一个数据作为基准，就会使数据变成一颗单分支的二叉树结构，此时的时间复杂度会增大，所以我们为了避免这样的情况，这里需要尽可能的使基准定到数组中间的位置。

public static void quickSort(int[] array) {quick(array,0,array.length-1);}private static void quick(int[] array,int start,int end ){if(start>=end){return ;}int index = midOfThree(array,start,end);swap(array,index,start);int pivot = partition(array,start,end);quick(array,start,pivot-1);quick(array,pivot+1,end);}private static int midOfThree(int[] array, int left , int right){//三数取中，优化基准的位置int mid = (left+right)/2;if (array[left] < array[right]) {if(array[mid]<array[left]){return left;}else if(array[mid]>array[right]){return right;}else{return mid;}}else{if(array[mid]>array[left]){return left;}else if(array[mid]<array[right]){return right;}else{return mid;}}}

快速排序的特性

1. 快速排序整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序

2. 时间复杂度：O(N*logN)

3. 空间复杂度：O(logN)

4. 稳定性：不稳定

归并排序

归并排序是一种二叉树结构的排序，核心思想就是把一组数据分成多分，然后再合并成有序的数组

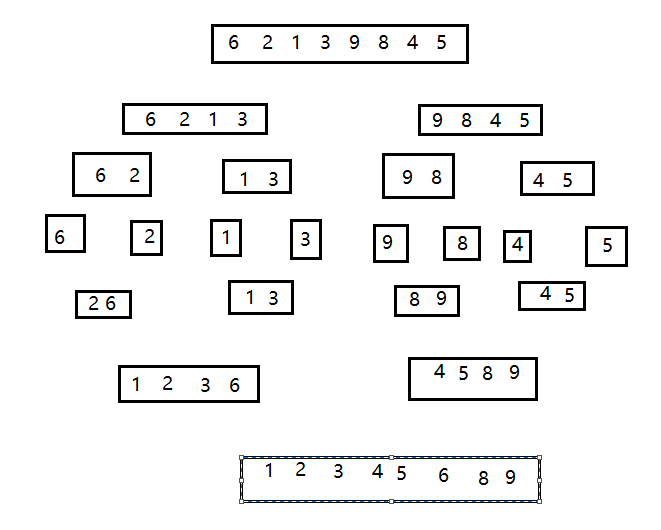
代码实现

public static void mergeSort(int[] array) {mergeSortFunction(array,0,array.length-1);}private static void mergeSortFunction(int[] array , int left ,int right) {if(left >=right){return ;}int mid = (left + right )/2;mergeSortFunction(array,left,mid);mergeSortFunction(array,mid+1,right);merge(array,left,right,mid);}private static void merge(int[] array,int left , int right , int mid) {int[] tempArray = new int[right-left+1];int s1 = left;int s2 = mid +1 ;int i = 0 ;while(s1<=mid&&s2<=right){if(array[s1]>=array[s2]){tempArray[i] = array[s2];i++;s2++;}else{tempArray[i] = array[s1];i++;s1++;}}while (s1<=mid){tempArray[i]=array[s1];i++;s1++;}while (s2<=right){tempArray[i]=array[s2];i++;s2++;}for (int j = 0; j < tempArray.length; j++) {array[j+left] = tempArray[j];}}

归并排序的特性

1. 归并的缺点在于需要O(N)的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序问题。

2. 时间复杂度：O(N*logN)

3. 空间复杂度：O(N)

4. 稳定性：稳定