一、摘要

尽管卷积神经网络（CNN）在视觉识别任务上取得巨大成功，但其固有的固定几何结构（固定卷积采样网格、固定池化窗口、固定 RoI 划分）严重限制了对未知几何变换（尺度、姿态、形变、视角变化）的建模能力。
本文提出可变形卷积网络（Deformable ConvNets），通过两个轻量级模块——可变形卷积（Deformable Convolution）与可变形 RoI 池化（Deformable RoI Pooling）——在无额外监督的前提下，为卷积/池化的空间采样位置施加可学习的偏移量，使网络可自适应地、密集地、端到端地建模复杂几何变换。
实验表明，Deformable ConvNets 在 PASCAL VOC 语义分割、Cityscapes 语义分割、PASCAL VOC 与 COCO 目标检测任务上均取得显著增益：

在 ResNet-101 主干上，DeepLab VOC mIoU 从 69.7 提升到 75.2；
COCO R-FCN mAP@[0.5:0.95] 从 30.8 提升到 34.5；
仅增加 <1% 参数与 <5% 计算量。

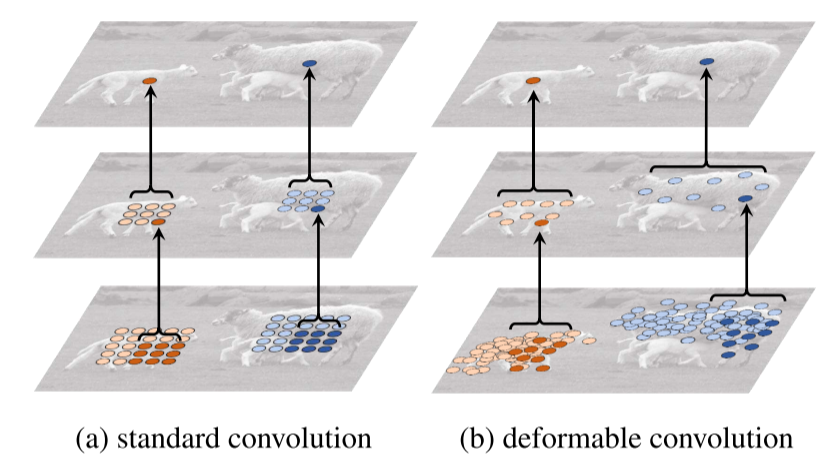
二、先前背景

在视觉识别中，如何适应几何变化或建模物体尺度、姿态、视角和部件变形等几何变换是核心挑战。

近年来，卷积神经网络（CNNs）在图像分类、语义分割和目标检测等视觉识别任务中取得显著成功。但其几何变换建模能力主要依赖大量数据增强、大模型容量以及一些简单的手工设计模块（如用于小平移不变性的最大池化），仍存在一些缺陷。

类别	具体内容
传统方法	1. 构建具有足够所需变化的训练数据集：通过仿射变换等数据增强方式实现，虽能从数据中学习鲁棒表示，但需付出高昂训练成本和复杂模型参数的代价。 2. 手工不变特征：SIFT、HOG、ORB 等依赖先验参数化变换，难以应对复杂或非参数化形变。
基于 CNN 的方法	AlexNet、VGG、ResNet 等通过堆叠卷积、池化获得层级特征。但所有采样位置固定，依然依赖原始边界框的特征提取，这并非最优，尤其面对非刚性物体
CNN 的局限	卷积核采样网格固定（如 3×3 网格），池化窗口固定（如 2×2），RoI 池化将任意形状区域强行划分为 k×k 固定 bin，无法适应物体尺度、姿态、部件形变。

类别

具体内容

传统方法

1. 构建具有足够所需变化的训练数据集：通过仿射变换等数据增强方式实现，虽能从数据中学习鲁棒表示，但需付出高昂训练成本和复杂模型参数的代价。

2. 手工不变特征：SIFT、HOG、ORB 等依赖先验参数化变换，难以应对复杂或非参数化形变。

基于 CNN 的方法

AlexNet、VGG、ResNet 等通过堆叠卷积、池化获得层级特征。

但所有采样位置固定，依然依赖原始边界框的特征提取，这并非最优，尤其面对非刚性物体

CNN 的局限

卷积核采样网格固定（如 3×3 网格），池化窗口固定（如 2×2），RoI 池化将任意形状区域强行划分为 k×k 固定 bin，无法适应物体尺度、姿态、部件形变。

相关的改进尝试：

方法名称	核心思想	与本文的差异
Spatial Transformer Networks (STN)	通过全局参数化（仿射/薄板样条）对整张特征图做一次性 warping	全局变换，无法对不同空间位置分别建模
Active Convolution	在卷积核采样点上增加可学习偏移，但偏移量为静态参数（训练完成后固定），且所有位置共享	偏移量不随输入变化，缺乏内容自适应性
Atrous / Dilated Convolution	通过固定膨胀率（dilation）扩大感受野	采样模式人工设定
Deformable Part Models (DPM)	用部件形变建模物体（如 HOG+DPM）	浅层模型，表达能力有限
Spatial Pyramid Pooling (SPP)	手工设计多尺度、多区域池化	区域划分人工设定
Transformation-Invariant Features	设计对特定变换不变的特征（如 SIFT、ORB、TI-pooling、Harmonic Networks 等）	变换类型需先验已知

上述 6 类方法均试图解决 CNN 的几何不变性，但要么全局/手工/静态，要么局限于已知变换。
本文的可变形卷积/可变形 RoI 池化首次实现了局部、密集、可学习、端到端的几何建模，可直接替换现有模块，无需额外监督。

三、先前存在的问题

问题类别	具体描述
固定几何结构	卷积核采样点集合 R 始终为规则网格，无法适应局部几何变化。
全局参数化限制	STN 仅支持全局、单一变换，无法对不同空间位置施加不同形变。
手工规则	空洞卷积的膨胀率需预先设定，且在所有位置共享。
非刚性对齐缺失	RoI Pooling 将任意形状物体强行划分为 k×k 固定 bin，导致特征与部件错位。
端到端学习缺失	传统可变形部件模型（DPM）需启发式训练，无法与 CNN 联合优化。

四、本文技术

4.1 可变形卷积（Deformable Convolution）

输入：特征图 $\boldsymbol{x} \in \mathbb{R}^{C \times H \times W}$ 。
标准卷积
2D 卷积包含两步，一是在输入特征图 x 上使用规则网格 R 采样，二是对采样值与权重 w 加权求和。对于输出特征图 y 上的每个位置 $p_0$ ，公式为：
$\mathbf{y}(\mathbf{p}_0) = \underset{\mathbf{p}_n \in \mathcal{R}}{\sum_{} }\mathbf{w}(\mathbf{p}_n) \cdot \mathbf{x}(\mathbf{p}_0 + \mathbf{p}_n)$
其中 R 为规则网格（如 $\mathcal{R}=\{(-1,-1),(-1,0), ...,(0,1),(1,1)\}$ 定义了一个 3×3、 dilation 为 1 的核。）
可变形卷积：
- 为规则网格 R 增加偏移量 $\{\Delta p_n | n=1,...,N\}$ ，偏移量由附加卷积层生成：
  $\displaystyle \mathrm{offset} = \mathrm{Conv}_{3 \times 3}(\mathbf{x}) \in \mathbb{R}^{2N \times H \times W}, \quad N = |\mathcal{R}|$
- 分数坐标处理：由于偏移量 $\Delta p_n$ 通常为分数，通过双线性插值实现：
  
  $x(p)=\underset{q}{\sum} G(q, p) \cdot x(q)$
  其中， $p$ 为任意（分数）位置（如式中的 $p_0 + p_n+\Delta p_n$ ）， $q$ 枚举特征图 x 中的所有整数空间位置， $G(\cdot, \cdot)$ 为双线性插值核，且可分离为两个一维核：
  $G(\mathbf{q}, \mathbf{p}) = g(q_x, p_x) \cdot g(q_y, p_y), \quad g(a, b) = \max(0, 1 - |a - b|)$
  
  后者的本质是 “线性权重”—— 两个坐标的距离越近，权重越大。

关于偏移量获取：通过对同一输入特征图应用卷积层获得偏移量，该卷积核与当前卷积层具有相同的空间分辨率和 dilation，输出偏移场与输入特征图空间分辨率相同，通道维度为 2N（对应 N 个 2D 偏移）。
偏移量并非手动设计，而是通过一个额外的卷积层从输入特征图中学习得到（对应图 2 中 “conv offset field” 模块）。
这个用于生成偏移量的卷积核，与当前可变形卷积层的卷积核具有相同的空间分辨率（如 3×3）和 dilation 系数（如 dilation=1）。例如，若当前可变形卷积使用 3×3 kernel、dilation=1，则生成偏移量的卷积层也采用 3×3 kernel、dilation=1。
这一设计确保偏移量的学习与特征提取的 “感受野范围” 匹配，使偏移量能精准捕捉局部几何变形。

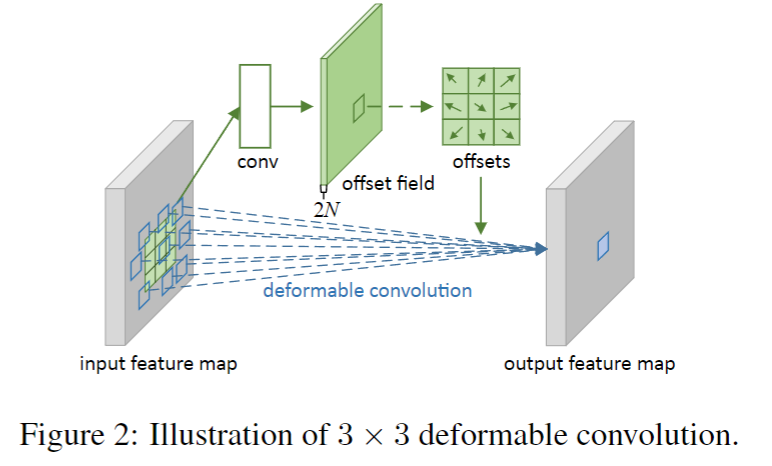
关于枚举q：实际上，为了提高计算效率，q枚举的通常仅仅是其整数邻域的空间位置，而不是所有整数空间位置。例如，假设在输入特征图上，需要计算非整数位置 $p = (1.2, 2.7)$ 的特征值 $x(p)$ ：
确定周围 4 个整数点： $q_1=(1,2)$ 、 $q_2=(1,3)$ 、 $q_3=(2,2)$ 、 $q_4=(2,3)$ 。
计算 x 方向权重：
$g(q_{x}=1, p_x=1.2) = 1 - |1 - 1.2| = 0.8$ ；
$g(q_{x}=2, p_x=1.2) = 1 - |2 - 1.2| = 0.2$ 。
计算 y 方向权重：
$g(q_{y}=2, p_y=2.7) = 1 - |2 - 2.7| = 0.3$ ；
$g(q_{y}=3, p_y=2.7) = 1 - |3 - 2.7| = 0.7$ 。
计算二维权重：
$G(q_1, p) = 0.8 \times 0.3 = 0.24$ ；
$G(q_2, p) = 0.8 \times 0.7 = 0.56$ ；
$G(q_3, p) = 0.2 \times 0.3 = 0.06$ ；
$G(q_4, p) = 0.2 \times 0.7 = 0.14$ 。
最终插值结果： $x(p) = 0.24x(1,2) + 0.56x(1,3) + 0.06x(2,2) + 0.14x(2,3)$

4.2 可变形 RoI 池化（Deformable RoI Pooling）

输入：特征图 $x$ 、RoI 参数 $(\mathbf{p}_0, w, h)$ 。
标准 RoI 池化
- $bin(i,j)$ 为第 $(i,j)$ 个 bin 在输入特征图 x 上对应的像素集合
  对于第 $(i,j)$ 个 bin：该 bin 的范围为：
  $\left\lfloor \frac{i \cdot w}{k} \right\rfloor \leq p_x < \left\lceil \frac{(i + 1) \cdot w}{k} \right\rceil$ 和 $\left\lfloor \frac{j \cdot h}{k} \right\rfloor \leq p_y < \left\lceil \frac{(j + 1) \cdot h}{k} \right\rceil$ 。
- P₀ 是 RoI 的左上角坐标（原点在特征图左上角）。
- p 是相对坐标，表示在 RoI 内部的位置（从 (0, 0) 到 (w-1, h-1)）。
- $n_{ij}$ 为 bin 中的像素数量。
- RoI 池化将其分为 $k\times k$ 个 bin，输出 $k\times k$ 特征图
  - 假设：RoI 宽 w=5，高 h=3，划分为 2×2 bins。则：
  - Bin(0,0) 的 x 范围：[0, 2)，y 范围：[0, 1)。
  - Bin(1,1) 的 x 范围：[2, 5)，y 范围：[1, 3)。
可变形 RoI 池化
- 先通过标准 RoI 池化，把任意 RoI 变成 $k\times k$ 特征图。
- 把 $k\times k$ 特征图拉平 → 全连接层 → 输出 $k\times k\times2$ 个归一化偏移 $\Delta \hat{\mathbf{p}}_{ij}$ （2代表x和y）；
- 将归一化偏移映射到实际像素偏移： $\gamma = 0.1$ ， $\Delta \mathbf{p}_{ij} = \gamma \cdot \Delta \hat{\mathbf{p}}_{ij} \odot (w, h)$
- 每个 bin 的位置平移 $\Delta \mathbf{p}_{ij}$ 后，用双线性插值取像素值，再做平均池化得到 y(i, j)。

4.3 位置敏感可变形 RoI 池化（Deformable PS RoI pooling）

标准 PS RoI 池化
- 目的：把任意 RoI 变成固定 $k\times k$ 特征，同时保持“位置敏感”——每个 bin 只响应特定空间位置。
- 基本步骤：
  - 用 1×1 卷积 把特征图变成 $k^2(C+1)$ 张 位置敏感得分图
  - 对 每个 bin(i,j)，只在 对应的那张得分图 X_{i,j,c} 上做 平均池化，得到该 bin 的值。
可变形 PS RoI 池化
- 基本步骤：
  - 用 1×1 卷积 把特征图变成 $k^2(C+1)$ 张 位置敏感得分图
  - 使用全卷积生成全分辨率偏移场，如使用 $3\times 3$ 卷积会变成 $2k^2(C+1)$
  - 从偏移场提取 RoI 对应的归一化偏移
  - 还原实际偏移并采样

可变形PS Rol池化与可变形 RoI 池化类似，但输入替换为特定的位置敏感得分图 $x_{i,j}$ 。偏移学习遵循全卷积思想，通过卷积层生成全空间分辨率偏移场，对每个 RoI（及每个类别）应用 PS RoI 池化获得归一化偏移，再转换为实际偏移。
简单说，可变形 PS RoI Pooling =
“先全卷积生成 k²(C+1) 张位置敏感得分图 + 2k²(C+1) 张全图偏移场，再用 PS Pooling 把每个 RoI 对应的偏移裁剪出来，还原后做可变形采样”，
既保留 位置敏感 又实现 部件级自适应对齐，全程 全卷积，无需逐 RoI 跑 fc。

4.4 可变形卷积网络构建

可变形卷积和 RoI 池化模块与对应普通版本的输入输出相同，可直接替换。训练时，用于偏移学习的新增卷积和全连接层初始化为零权重，学习率设为现有层的 β 倍（默认 β=1，Faster R-CNN 中的全连接层 β=0.01），通过上述插值操作的反向传播进行训练，形成可变形卷积网络（deformable ConvNets）。

在特征提取方面，采用 ResNet-101 和改进的 Aligned-Inception-ResNet 架构，移除平均池化和全连接层，添加 1×1 卷积降低通道维度至 1024，调整最后卷积块的步长和 dilation 以提高特征图分辨率，并在最后几个卷积层（ kernel size>1）应用可变形卷积（实验发现 3 层为不同任务的良好权衡）。

在分割和检测网络方面，基于特征提取网络的输出特征图构建任务特定网络，如 DeepLab 用于语义分割，Category-Aware RPN、Faster R-CNN 和 R-FCN 用于目标检测，且 Faster R-CNN 和 R-FCN 中的 RoI 池化层可替换为可变形 RoI 池化。

五、创新点

创新维度	具体贡献
可变形卷积	首次在卷积内部引入逐位置可学习的偏移量，实现局部、密集、内容自适应的几何变换建模，且端到端训练。
可变形 RoI 池化	首次在 RoI 池化中引入逐 bin 可学习的偏移量，实现部件级自适应对齐，显著提升非刚性物体检测。
轻量级	仅增加 2N 个通道（卷积）或 2k² 个通道（PS RoI），参数增量 <1%，计算量增量 <5%。
通用性	可直接替换现有 CNN 中的标准卷积/RoI 池化，无需改动网络整体结构。
首次验证	首次在密集预测任务（语义分割、目标检测）上验证可学习密集几何变换的有效性。

六、本文技术的潜在问题

问题类别	具体描述
偏移量学习稳定性	偏移量初始化为 0，若学习率设置不当，可能导致训练初期梯度消失或爆炸。
计算开销	虽然整体开销小，但在极端大分辨率输入（如 4K）下，2N 额外通道仍会带来显存压力。
可解释性	偏移量分布缺乏显式约束，可能学习到不符合物理意义的采样模式（如采样到图像外）。
任务依赖性	偏移量完全由目标任务驱动，对新任务或跨域场景可能需重新训练。
稀疏监督风险	在目标检测中，若标注框质量差，偏移量可能学到噪声，导致性能下降。
小目标和细节处理能力有限	虽然可变形卷积能自适应调整感受野，但在处理小目标或精细结构时，偏移量的学习可能受限于特征图分辨率和感受野大小，导致定位精度不足。

七、未来可改善的方向

方向类别	具体建议
增强对小目标和细节的处理	结合特征金字塔网络等技术，提高小目标和精细结构区域的特征图分辨率；设计针对小目标的专用可变形卷积模块，调整感受野大小和偏移量学习策略，提升定位精度。
跨域泛化	引入元学习或域自适应，使偏移量快速适应新任务或新场景。
结构搜索	用 NAS（Neural Architecture Search）自动搜索最佳偏移量生成网络结构。
多模态融合	将偏移量与深度、光流、边缘等额外模态联合学习，提升几何建模能力。
更大尺度	将可变形思想扩展到 3D 卷积、Transformer 自注意力机制，处理视频或点云。