二叉搜索树的数据结构

手写实现二叉搜索树

树节点定义

插入节点

源码

流程图

二叉树插入步骤图解

第一步: 插入 20

第二步: 插入 10

第三步: 插入 30

第四步: 插入 5

查找节点

源码

场景一: 查找成功 (search for 25)

第一步: 从根节点开始

第二步: 移动到右子树

第三步: 找到目标

场景二: 查找失败 (search for 12)

第一步: 从根节点开始

第二步: 移动到左子树

第三步: 继续向右查找

删除节点

源码

核心删除逻辑: delete(Node delNode)

BST 删除节点实例图解

场景一: 删除叶子节点 (Delete 5)

场景二: 删除只有一个孩子的节点 (Delete 15)

场景三: 删除有两个孩子的节点 (Delete 20)

第 1 步: 识别目标 (delNode) 与后继 (miniNode)

第 2 步: 处理后继节点的子树 (第一次 transplant)

第 3 步: 连接后继节点与待删节点的右子树

第 4 步: 将后继节点换到待删位置 (第二次 transplant)

第 5 步: 连接后继节点与待删节点的左子树 (最终状态)

常见问题

二叉搜索树结构简述&变T的可能也让手写

二叉搜索树的插入、删除、索引的时间复杂度

二叉搜索树删除含有双子节点的元素过程叙述

二叉搜索树的节点都包括了哪些信息

为什么Java HashMap 中说过红黑树而不使用二叉搜索树

二叉搜索树的数据结构

二叉搜索树（Binary Search Tree），也称二叉查找树。如果你看见有序二叉树（Ordered Binary tree）、排序二叉树（Sorted Binary Tree）那么说的都是一个东西。

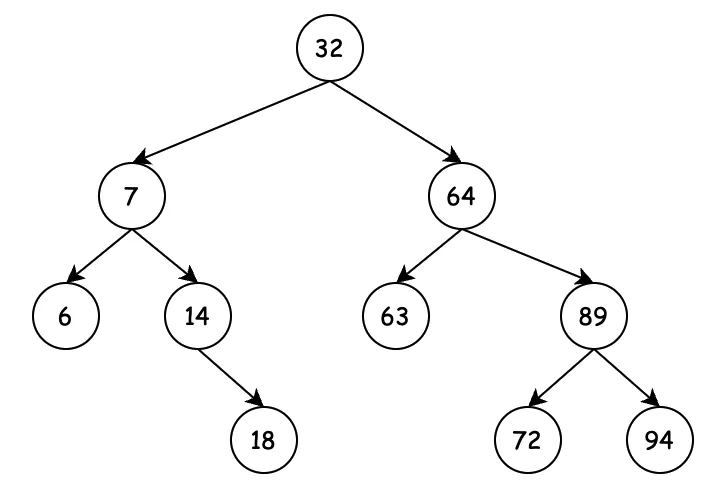
若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
任意节点的左、右子树也分别为二叉查找树；

手写实现二叉搜索树

树节点定义

public class Node {public Class<?> clazz;public Integer value;public Node parent;public Node left;public Node right;public Node(Class<?> clazz, Integer value, Node parent, Node left, Node right) {this.clazz = clazz;this.value = value;this.parent = parent;this.left = left;this.right = right;}@Overridepublic int hashCode() {final int prime = 31;int result = 1;result = prime * result + ((value == null) ? 0 : value.hashCode());return result;}@Overridepublic boolean equals(Object obj) {if (this == obj) return true;if (null == obj) return false;if (getClass() != obj.getClass()) return false;Node node = (Node) obj;if (null == value) {return node.value == null;} else {return node.value.equals(value);}}
}

插入节点

源码

public Node insert(int e) {if (null == root) {root = new Node(e, null, null, null);size++;return root;}// 索引出待插入元素位置，也就是插入到哪个父元素下Node parent = root;Node search = root;while (search != null && search.value != null) {parent = search;if (e < search.value) {search = search.left;} else {search = search.right;}}// 插入元素Node newNode = new Node(e, parent, null, null);if (parent.value > newNode.value) {parent.left = newNode;} else {parent.right = newNode;}size++;return newNode;
}

流程图

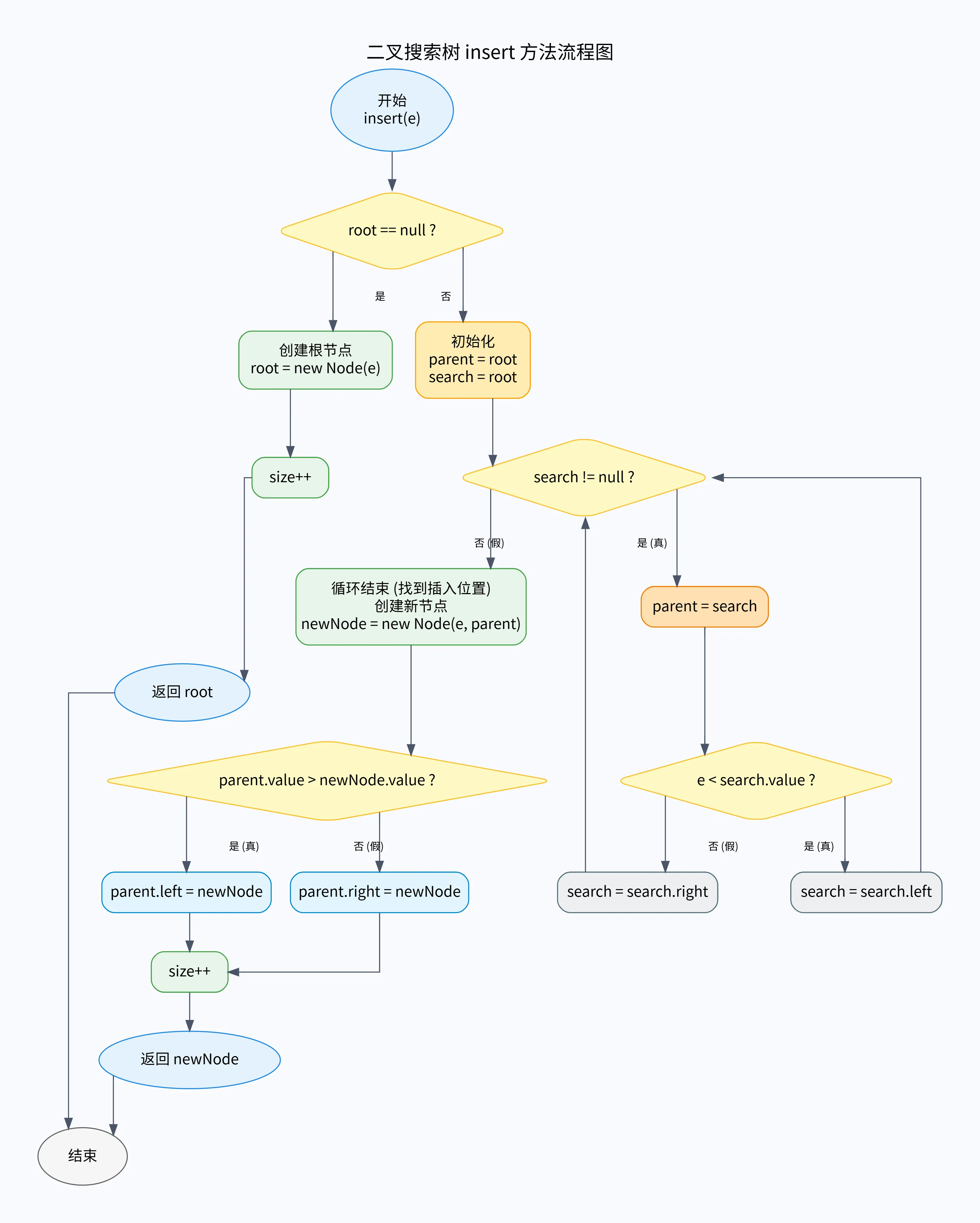
二叉树插入步骤图解

以一个简单的例子，依次插入数组 [20, 10, 30, 5] 中的四个数字，并画出每一步操作后树的结构变化。

第一步: 插入 20

执行操作: 调用 insert(20)。
代码路径: 此时树是空的，root 为 null。代码执行第一个 if 分支，创建一个新的根节点，其值为20。

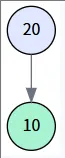
第二步: 插入 10

执行操作: 调用 insert(10)。
代码路径: root (20) 不为 null。进入 while 循环：

将 10 与根节点 20 比较，因为 10 < 20，所以 search 指针移动到左子节点 (当前为 null)。
search 变为 null，循环结束。此时的 parent 仍然是节点 20。
创建一个值为 10 的新节点，并将其作为 parent (节点20) 的左孩子。

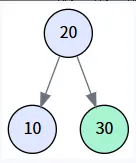
第三步: 插入 30

执行操作: 调用 insert(30)。
代码路径: root (20) 不为 null。进入 while 循环：

将 30 与根节点 20 比较，因为 30 > 20，所以 search 指针移动到右子节点 (当前为 null)。
search 变为 null，循环结束。此时的 parent 仍然是节点 20。
创建一个值为 30 的新节点，并将其作为 parent (节点20) 的右孩子

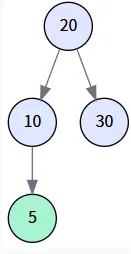
第四步: 插入 5

执行操作: 调用 insert(5)。
代码路径: root (20) 不为 null。进入 while 循环：

第1轮循环: 5 < 20，search 移动到左孩子 (节点10)。parent 更新为节点 20。
第2轮循环: 5 < 10，search 移动到左孩子 (当前为 null)。parent 更新为节点 10。
search 变为 null，循环结束。此时的 parent 是节点 10。
创建一个值为 5 的新节点，并将其作为 parent (节点10) 的左孩子。

查找节点

源码

public Node search(int e) {Node node = root;while (node != null && node.value != null && node.value != e) {if (e < node.value) {node = node.left;} else {node = node.right;}}return node;
}

初始树结构
假设我们的树通过依次插入 `[20, 10, 30, 5, 15, 25, 35]` 构建而成。

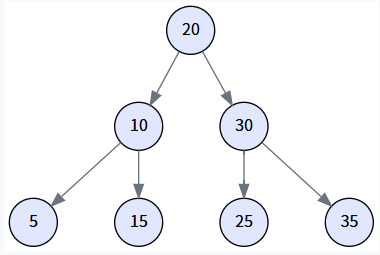
场景一: 查找成功 (search for 25)

我们来查找一个存在于树中的值：`25`。

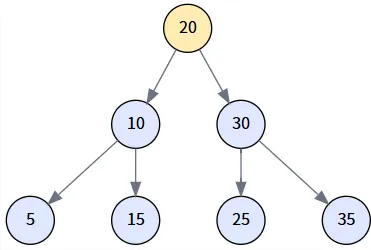
第一步: 从根节点开始

当前节点 node: 20
比较: `25 < 20` 为假。
操作: 进入 `else` 分支，将 node 更新为其右孩子。node = node.right。

第二步: 移动到右子树

当前节点 node: 30
比较: `25 < 30` 为真。
操作: 进入 `if` 分支，将 node 更新为其左孩子。node = node.left。

第三步: 找到目标

当前节点 node: 25
循环条件检查: `node.value != e` (即 `25 != 25`) 为假。
操作: 循环条件不满足，退出 while 循环。

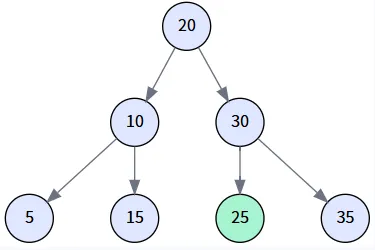
结果: 方法返回值为 25 的 Node 对象。

场景二: 查找失败 (search for 12)

现在，我们查找一个不存在于树中的值：`12`。

第一步: 从根节点开始

当前节点 node: 20
比较: `12 < 20` 为真，node 移动到左孩子 (10)。

第二步: 移动到左子树

当前节点 node: 10
比较: `12 < 10` 为假。
操作: 进入 `else` 分支，node 更新为其右孩子。node = node.right。

第三步: 继续向右查找

当前节点 node: 15
比较: `12 < 15` 为真。
操作: 进入 `if` 分支，node 更新为其左孩子。

第四步: 到达叶节点末端

当前节点 node: `null` (因为节点 15 没有左孩子)。
循环条件检查: `node != null` 为假。
操作: 循环条件不满足，退出 while 循环。

树的结构保持不变，但我们的 node 指针现在是 null。

结果: 方法返回 null，表示未找到值为 12 的节点。

删除节点

源码

public Node delete(int e) {Node delNode = search(e);if (null == delNode) return null;return delete(delNode);
}private Node delete(Node delNode) {if (delNode == null) return null;Node result = null;if (delNode.left == null) {result = transplant(delNode, delNode.right);} else if (delNode.right == null) {result = transplant(delNode, delNode.left);} else {// 因为删除的节点，有2个孩子节点，这个时候找到这条分支下，最左侧做小的节点。用它来替换删除的节点Node miniNode = getMiniNode(delNode.right);if (miniNode.parent != delNode) {// 交换位置，用miniNode右节点，替换miniNodetransplant(miniNode, miniNode.right);// 把miniNode 提升父节点，设置右子树并进行挂链。替代待删节点miniNode.right = delNode.right;miniNode.right.parent = miniNode;}// 交换位置，删除节点和miniNode 可打印测试观察；System.out.println(this);transplant(delNode, miniNode);// 把miniNode 提升到父节点，设置左子树并挂链miniNode.left = delNode.left;miniNode.left.parent = miniNode;result = miniNode;}size--;return result;
}
private Node getMinimum(Node node) {while (node.left != null) {node = node.left;}return node;
}private Node transplant(Node delNode, Node addNode) {if (delNode.parent == null) {this.root = addNode;}// 判断删除元素是左/右节点else if (delNode.parent.left == delNode) {delNode.parent.left = addNode;} else {delNode.parent.right = addNode;}// 设置父节点if (null != addNode) {addNode.parent = delNode.parent;}return addNode;
}

核心删除逻辑: delete(Node delNode)

这是处理删除操作的核心方法。它分为三个主要分支：

情况1: 要删除的节点没有左孩子。
情况2: 要删除的节点有左孩子，但没有右孩子。
情况3: 要删除的节点有两个孩子（最复杂的情况）。

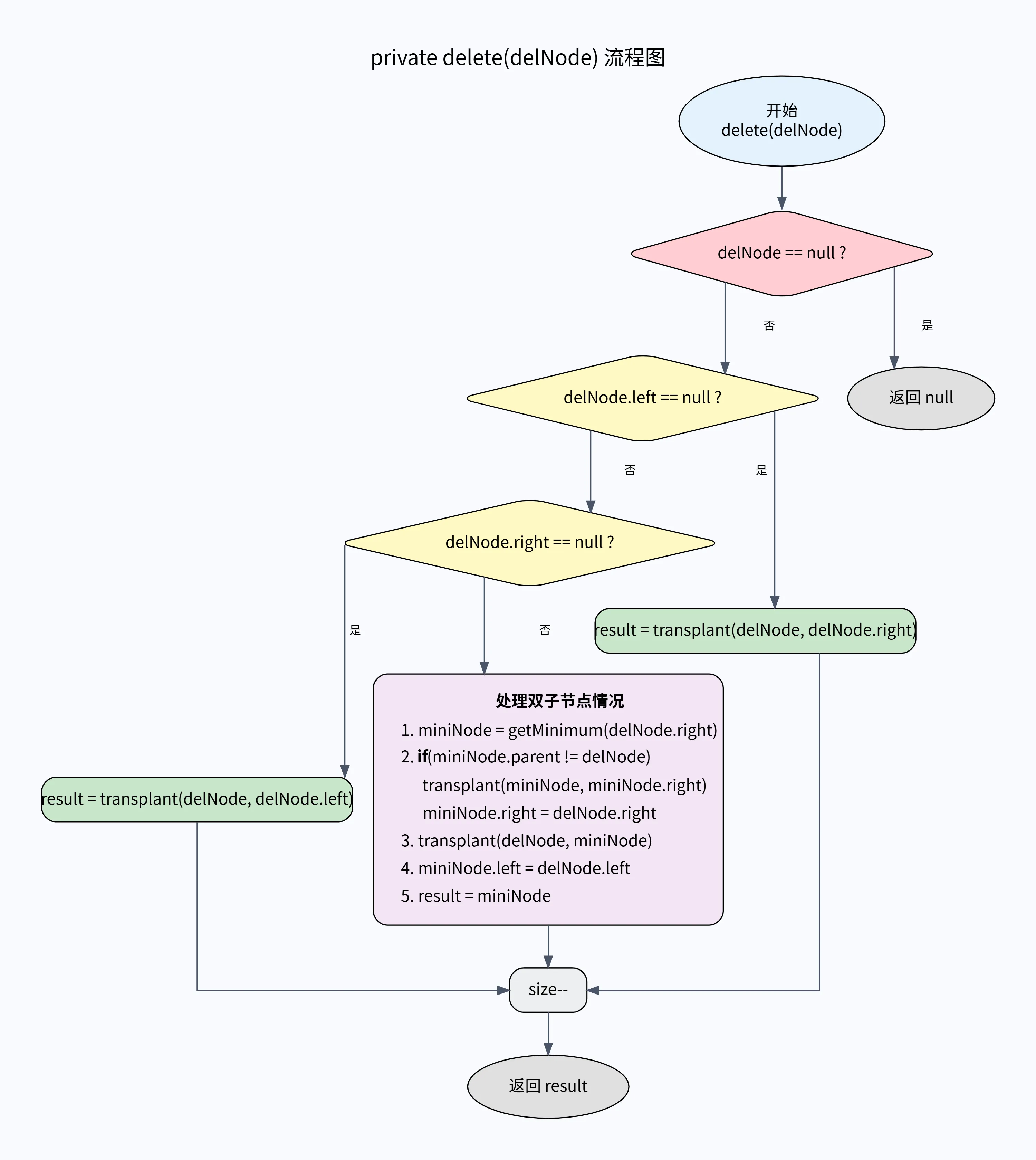transplant 方法是实现删除的核心。它的作用是在树中用一个节点 (addNode) 替换另一个节点 (delNode)，并正确地维护父节点的链接关系。它本身并不处理子节点的链接，这由 delete 方法完成。
getMinimum 是一个简单的辅助方法，用于在给定的子树中找到值最小的节点。它通过不断地沿着左子节点向下遍历直到末端来实现。

BST 删除节点实例图解

我们将使用一个具体的二叉搜索树来逐步演示删除操作的三个场景。在图示中：

红色节点: 将要被删除的目标节点 (delNode)。
黄色节点: 用于替换的后继节点 (miniNode)。
紫色边: 表示正在发生改变的父子链接。

初始树结构
我们的示例树通过依次插入 `[20, 10, 30, 5, 15, 25, 35]` 构建而成。

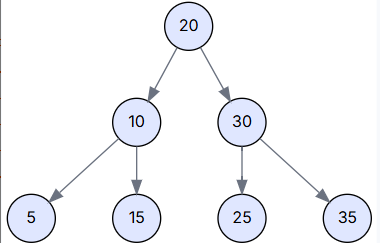
场景一: 删除叶子节点 (Delete 5)

执行步骤

delete(5) 调用 search(5) 找到节点 5。
进入 delete(Node delNode) 方法，delNode 是节点 5。
检查 delNode.left == null 为真。
调用 transplant(delNode, delNode.right)，即 transplant(5, null)。
在 transplant 中，delNode 的父节点 (10) 的左孩子 (left) 被设置为 null。
删除完成。

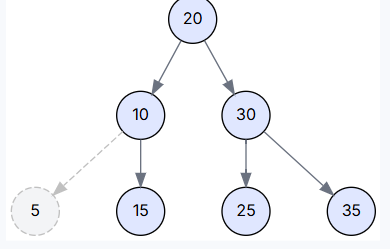
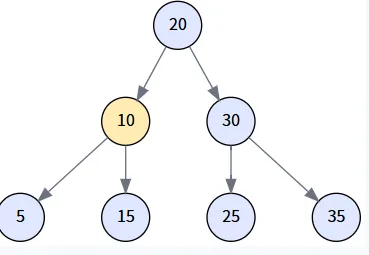
场景二: 删除只有一个孩子的节点 (Delete 15)

注: 为演示此场景，我们创建一棵新树 `[20, 10, 30, 5, 15, 35]`，其中节点 15 只有一个左孩子 5。我们会用它的子节点替换它。

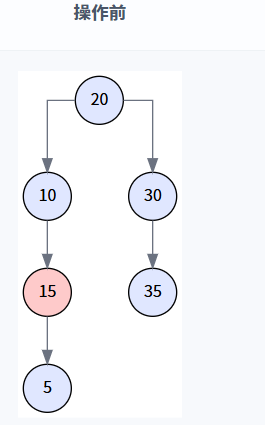
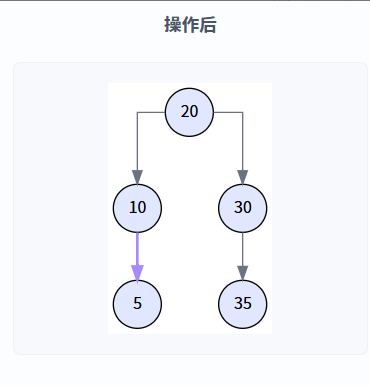
执行逻辑: transplant(15, 5) 被调用，节点 10 的右孩子指针直接指向了节点 5，同时更新了节点 5 的父指针。

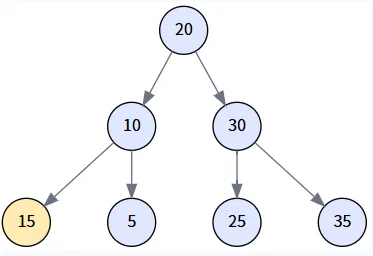
场景三: 删除有两个孩子的节点 (Delete 20)

这是最复杂的情况，我们将删除根节点 20。这会触发代码中最完整的逻辑：寻找后继节点 (右子树的最小值)，并用它来替换被删除的节点。

第 1 步: 识别目标 (delNode) 与后继 (miniNode)

我们想删除 20。因为它有两个孩子，我们必须找到它的后继节点。通过 `getMinimum(delNode.right)`，我们找到其右子树 (以30为根) 的最小值，即 25。

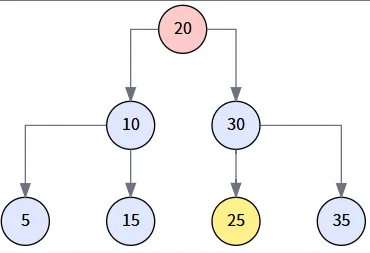
第 2 步: 处理后继节点的子树 (第一次 transplant)

代码检查 `miniNode.parent != delNode` (即 30 != 20)，这个条件为真。因此，我们需要先将 `miniNode` (25) 提拔上来。我们调用 transplant(miniNode, miniNode.right)，即 transplant(25, null)，将 25 原来的父节点 (30) 的左孩子指向 25 的右孩子 (null)。

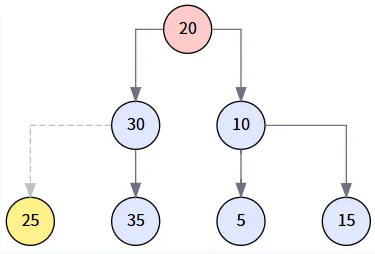
第 3 步: 连接后继节点与待删节点的右子树

执行 miniNode.right = delNode.right。我们将 20 的右子树 (以 30 为根) 变成 25 的右子树。

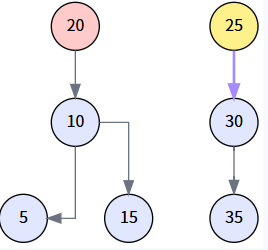
第 4 步: 将后继节点换到待删位置 (第二次 transplant)

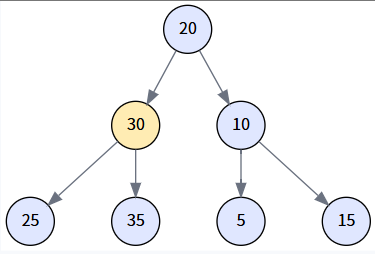
调用 transplant(delNode, miniNode)，即 transplant(20, 25)。因为 20 是根节点，这会将树的 root 指针更新为 25。

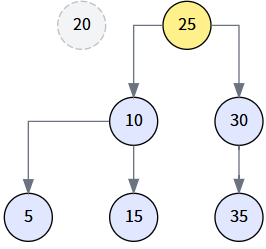
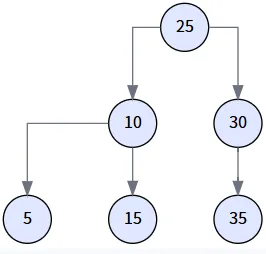
第 5 步: 连接后继节点与待删节点的左子树 (最终状态)

最后，执行 miniNode.left = delNode.left，将 20 的左子树 (以 10 为根) 挂到 25 的左边，完成整个删除操作。

常见问题

二叉搜索树结构简述&变T的可能也让手写

某个节点的左子树所有值都小于该节点，右子树中所有值都大于该节点

二叉搜索树的插入、删除、索引的时间复杂度

插入、删除、查找的时间复杂度取决于树的高度

理想情况下是 O(log n), 但最坏情况下会退化为 O(n)

二叉搜索树删除含有双子节点的元素过程叙述

删除一个有两个子节点的节点时，不能直接删除掉它，而是从它的右子树中找一个最小的节点（刚好比他大一点点），用这个节点来顶替他的位置。
例如：删除节点 delNode 他有两个子节点 delNode.left、delNode.right

从它的右子树中找一个合适的节点来替代它 addNode
因为要用 addNode 节点来替换 delNode，所以需要先把 addNode 原来的位置清理干净，最多只有一个右孩子（没有左孩子），用右孩子来替换 addNode的位置
把delNode的父节点指向 addNode 、把delNode的左右子树接到 addNode上面