简介：Bezier曲线是计算机图形学中用于创建平滑曲线的重要工具，广泛应用于图形设计、游戏开发、CAD系统等领域。本文深入探讨了Bezier曲线的基础知识，并详细说明了如何在Visual Basic中使用 Graphics 对象的 DrawBezier 方法绘制曲线。通过理论学习和实践操作，读者将掌握调整控制点以实现曲线平滑的技巧，增强在图形编程方面的能力。

1. Bezier曲线概念与应用

在现代计算机图形学中，Bezier曲线作为一项基础且强大的工具，在各个领域中扮演着极其重要的角色。不论是网页设计、图形设计、游戏开发还是CAD系统，Bezier曲线都以其实现路径平滑、形状编辑简便的特点获得了广泛的应用。简单来说，Bezier曲线是一种通过控制点来定义路径的数学模型。通过增加控制点的数量和位置，我们可以创建从直线到复杂曲线的各种图形。在下一章节中，我们将深入探索Bezier曲线的数学原理，以及如何在实际应用中利用这些原理来实现更加丰富的视觉效果。

2. Bezier曲线的数学原理

2.1 Bezier曲线的定义和特性

2.1.1 Bezier曲线的几何解释

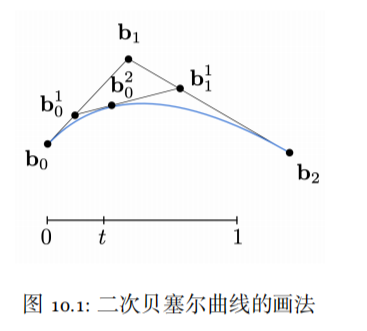
Bezier曲线是一种参数曲线，它通过一组称为“控制点”的点来定义。这条曲线最显著的特性之一是它不一定会穿过每一个控制点，而是由这些点来“引导”曲线的形状。在几何解释上，可以将Bezier曲线看作是控制点定义的多边形边缘的“平滑化”。

让我们来看一个二次Bezier曲线的例子。一个二次Bezier曲线由三个控制点定义：

P0（起点）
P1（控制点）
P2（终点）

这个二次Bezier曲线可以被解释为P0和P2之间的线段按照P1的位置进行弯曲的结果。随着参数t从0变化到1，曲线上的点依次通过点P0、P1和P2，定义了一个平滑的过渡路径。通过调整P1的位置，可以控制曲线的弯曲程度和方向。

2.1.2 Bezier曲线的代数形式

从代数的角度来说，Bezier曲线可以用基函数和控制点坐标来表达。对于二次Bezier曲线，其数学表达式如下：

[ B(t) = (1 - t)^2 \cdot P0 + 2 \cdot (1 - t) \cdot t \cdot P1 + t^2 \cdot P2 ]

其中，( B(t) ) 表示曲线上在参数t处的点，( P0, P1, P2 )是控制点坐标，t是参数，取值范围在[0, 1]之间。这个公式可以用来计算曲线上任何点的位置。

在实际应用中，参数t常常被看作是时间或者迭代步长，使得我们可以沿着曲线插值计算出一系列的点，这些点可以用来绘制整个曲线的形状。

2.2 Bezier曲线的数学基础

2.2.1 参数方程和向量表示

Bezier曲线的参数方程使用向量形式表示，这种表示方式使得计算更为直观和方便。例如，一个三次Bezier曲线可以用四个控制点( P_0, P_1, P_2, P_3 )和参数( t )定义如下：

[ B(t) = (1 - t)^3 \cdot P_0 + 3 \cdot (1 - t)^2 \cdot t \cdot P_1 + 3 \cdot (1 - t) \cdot t^2 \cdot P_2 + t^3 \cdot P_3 ]

其中，( t )是一个在区间[0, 1]内的参数，( B(t) )是在参数t时刻曲线上点的向量表示。

2.2.2 控制点和基函数的作用

控制点是定义Bezier曲线形状的关键。每一个控制点都对曲线的形状有影响，而这种影响的大小由基函数决定。基函数，也称为Bernstein多项式，在Bezier曲线的方程中起到了分配参数t所代表的权重的作用。

对于二次Bezier曲线，其基函数是( (1 - t)^2, 2 \cdot (1 - t) \cdot t, t^2 )。
对于三次Bezier曲线，则是( (1 - t)^3, 3 \cdot (1 - t)^2 \cdot t, 3 \cdot (1 - t) \cdot t^2, t^3 )。

每个基函数随着参数t的变化，在0到1之间变化，这些变化对应了在曲线形状中不同控制点的“权重”。因此，通过调整控制点的位置，我们可以控制曲线在不同区段的弯曲程度。

2.3 Bezier曲线的构建和计算方法

2.3.1 递归细分算法

递归细分算法（也称为De Boor-Cox算法）是一种计算Bezier曲线的常用方法。这个算法的基本思想是将一条Bezier曲线分割成两条新的Bezier曲线，并递归地应用这一过程，直到曲线足够接近直线，或者达到所需的精度。

首先，将曲线等分为两部分，找到曲线的中点。
然后，将两部分继续细分，直至达到预定的分割深度。
在每次分割时，都会生成新的控制点。

这个过程可以用递归函数来实现，递归的基本步骤就是基于当前控制点计算新的控制点，然后对新控制点重复此过程。递归细分算法的伪代码如下：

function DeBoorCox(controlPoints, t, depth)if depth < threshold thenreturn CalculatePoint(controlPoints, t)end if// 分割控制点newControlPoints = SplitControlPoints(controlPoints)// 递归计算左半部分曲线leftCurve = DeBoorCox(newControlPoints.left, t, depth - 1)// 递归计算右半部分曲线rightCurve = DeBoorCox(newControlPoints.right, t, depth - 1)// 合并曲线return MergeCurves(leftCurve, rightCurve)
end function

2.3.2 De Casteljau算法详解

De Casteljau算法是另一种计算Bezier曲线的数值方法，它具有数值稳定性和几何不变性的优点，特别适合用于计算和绘制复杂度较高的Bezier曲线。算法基于一种称为仿射组合的概念，通过一系列的线性插值操作来计算曲线上的点。

De Casteljau算法的基本步骤如下：

在控制点上，进行线性插值以获得新的点集。
使用新的点集重复上述线性插值过程，直到只剩下一个点。
这个最终得到的点就是参数t对应的Bezier曲线上的一点。

function DeCasteljau(controlPoints, t)points = controlPointswhile length(points) > 1 donewPoints = []for i = 0 to length(points) - 2 donewPoints.append((1 - t) * points[i] + t * points[i + 1])end forpoints = newPointsend whilereturn points[0]
end function

这个算法的一个关键特点是，由于它的计算过程是基于线性插值的，所以可以直观地表示为控制点上的向量操作。De Casteljau算法的几何解释是，通过在控制点之间进行线性插值来逼近曲线，这为理解Bezier曲线提供了直观的几何理解。

3. Visual Basic中DrawBezier方法的使用

Visual Basic（简称VB）作为一种简单易用的编程语言，它提供了一些用于绘制图形和曲线的内置方法，其中 DrawBezier 方法允许用户绘制贝塞尔曲线。本章节将深入探讨如何在Visual Basic中使用 DrawBezier 方法来绘制贝塞尔曲线，包括其基础介绍、高级应用以及优化技巧。

3.1 DrawBezier方法基础介绍

3.1.1 方法的语法结构

DrawBezier 方法是 Graphics 类中的一个成员函数，用于绘制贝塞尔曲线。它接受四个点作为参数，分别为起点、两个控制点以及终点。下面展示的是 DrawBezier 方法的基本语法结构：

Public Sub DrawBezier(ByVal pen As Pen, ByVal pt1 As Point, ByVal pt2 As Point, ByVal pt3 As Point, ByVal pt4 As Point)

AI写代码vb

pen ：定义曲线颜色、宽度和其他样式属性的 Pen 对象。
pt1 、 pt2 、 pt3 、 pt4 ：分别是贝塞尔曲线的起点、第一个控制点、第二个控制点和终点。

3.1.2 参数详解和实例演示

在这部分，我们将通过一个实例演示来更深入地理解 DrawBezier 方法的使用。

Private Sub Form1_Paint(sender As Object, e As PaintEventArgs) Handles Me.PaintDim g As Graphics = e.Graphics' 创建一个Pen对象，用于定义绘制的样式Dim pen As New Pen(Color.Black, 2)' 定义贝塞尔曲线的起点、两个控制点和终点Dim pt1 As New Point(50, 50)Dim pt2 As New Point(100, 10)Dim pt3 As New Point(200, 190)Dim pt4 As New Point(250, 250)' 调用DrawBezier方法绘制贝塞尔曲线g.DrawBezier(pen, pt1, pt2, pt3, pt4)
End Sub

在这个示例中，我们创建了一个窗体应用程序，并在窗体的 Paint 事件处理程序中使用 DrawBezier 方法绘制了一条贝塞尔曲线。通过定义四个点，我们可以看到曲线从起点开始，经过第一个控制点和第二个控制点的"拉动"，最终到达终点。

3.2 DrawBezier方法的高级应用

3.2.1 结合图形用户界面的应用

在图形用户界面中， DrawBezier 方法可以用于绘制自定义的图形和动画效果。要结合GUI应用，通常需要将绘图代码放置在特定的事件处理程序中，例如按钮点击事件、定时器事件等。

在以下示例中，我们将创建一个按钮，点击该按钮时，在窗体上绘制一条新的贝塞尔曲线：

Private Sub Button1_Click(sender As Object, e As EventArgs) Handles Button1.Click' 调用绘制贝塞尔曲线的过程DrawBezierCurveOnForm()
End SubPrivate Sub DrawBezierCurveOnForm()Dim g As Graphics = Me.CreateGraphics()' 创建一个蓝色的Pen对象Dim pen As New Pen(Color.Blue, 3)' 定义新的贝塞尔曲线的点Dim pt1 As New Point(30, 30)Dim pt2 As New Point(150, 20)Dim pt3 As New Point(220, 200)Dim pt4 As New Point(300, 250)' 绘制贝塞尔曲线g.DrawBezier(pen, pt1, pt2, pt3, pt4)' 释放资源g.Dispose()
End Sub

3.2.2 与其他绘图方法的结合

为了创建更加丰富的视觉效果， DrawBezier 方法可以与其他绘图方法如 DrawLine 、 DrawRectangle 等结合使用。例如，可以先绘制一系列贝塞尔曲线来构建物体的轮廓，再利用其他绘图方法填充颜色和细节。

' 绘制物体轮廓的贝塞尔曲线
g.DrawBezier(pen, pt1, pt2, pt3, pt4)' 使用FillEllipse方法填充物体的某些部分
Dim brush As New SolidBrush(Color.Green)
g.FillEllipse(brush, x, y, width, height)' 使用DrawRectangle方法绘制物体的边缘
g.DrawRectangle(pen, x, y, width, height)

3.3 DrawBezier方法的优化技巧

3.3.1 性能优化策略

在使用 DrawBezier 方法绘制复杂图形或大量曲线时，性能可能成为关注点。优化策略包括减少不必要的绘图调用、缓存复杂图形的位图以及使用双缓冲技术。

例如，可以使用 Graphics 对象的 DrawCachedBitmap 方法来绘制预先缓存的位图，而不是每次都重新绘制整个图形。

3.3.2 错误处理和调试技巧

在复杂的绘图应用中，正确处理异常和进行调试是非常关键的。在使用 DrawBezier 方法时，必须确保所有使用的参数都是有效的，否则可能会抛出异常。

例如：

Tryg.DrawBezier(pen, pt1, pt2, pt3, pt4)
Catch ex As ExceptionMessageBox.Show("绘制失败: " & ex.Message)
End Try

这样可以捕获并处理绘图过程中可能出现的任何异常，并向用户显示错误消息。

通过上述章节内容的详细介绍，我们了解了 DrawBezier 方法在Visual Basic中的应用，以及如何结合GUI进行高级应用，以及一些常用的优化策略。下一章节将会详细探讨贝塞尔曲线控制点的调整与平滑技术，进一步深入理解贝塞尔曲线的高级操作。

4. Bezier曲线控制点的调整与平滑技术

4.1 控制点的作用和影响

4.1.1 控制点的直观理解

Bezier曲线通过控制点来定义曲线的形状和路径。这些控制点是构成Bezier曲线的几何基础，决定了曲线的整体形态和流线。直观上，我们可以将控制点看作是"拉力点"，它们通过"拉扯"曲线来影响其弯曲程度和方向。当移动一个控制点时，与之相关的曲线部分就会相应地弯曲或者拉直，从而产生新的形状。

4.1.2 如何影响曲线的形状

控制点影响曲线的形状遵循一定的数学规则。在二次和三次Bezier曲线中，曲线的起点和终点由首尾两个控制点确定。中间的控制点则决定了曲线的弯曲程度和曲线的"方向"。对于二次Bezier曲线，仅有一个中间控制点；而对于三次Bezier曲线，有两个中间控制点。

曲线平滑的关键在于控制点的合理布局。一个曲率变化平缓的曲线，需要控制点位置适当并且均匀分布。相反，如果需要曲线出现锐利的转折，则需要将控制点紧密地放置在一起，或者把它们移动到离曲线较远的位置。通过适当的控制点调整，可以实现从简单直线到复杂曲线的各种形状。

4.2 曲线平滑技术

4.2.1 平滑算法的原理

曲线平滑技术的核心在于调整控制点的位置，使得曲线上没有尖锐的转折点，整体看起来流畅自然。通常，算法会考虑以下几个方面：

控制点间距离：减少控制点之间的距离能够帮助平滑曲线。
控制点位置：改变控制点的位置来调整曲线弯曲的程度。
曲率连续性：确保曲线在各个控制点处曲率变化连续，无突变。

4.2.2 实现曲线平滑的具体方法

一个常用的平滑技术是使用迭代方法来微调控制点的位置。这种方法通常包括以下步骤：

对曲线上的点进行采样，确定需要平滑的区域。
分析采样点的曲率，识别曲率突变的点。
对于曲率突变的点，计算新的控制点位置，使得曲率变化更加平缓。
使用新的控制点重新绘制曲线，再次进行采样与分析，重复步骤2和3，直到曲线达到预定的平滑度。

4.3 动态调整控制点实现交互效果

4.3.1 用户输入和控制点的关联

在许多应用中，用户希望实时看到控制点调整对曲线形状的影响，这要求程序能够动态地响应用户的输入，并实时更新控制点的位置。例如，用户通过鼠标拖动控制点来调整曲线，程序需要捕捉鼠标的移动事件，并实时计算并更新控制点的新位置。这样可以给用户一种"所见即所得"的直观体验。

4.3.2 实时更新曲线的技术实现

实现曲线的实时更新，需要高效地执行以下步骤：

监听和捕捉用户的输入事件（如鼠标或触摸事件）。
根据用户操作计算控制点的新位置。
使用新的控制点位置重新绘制Bezier曲线。
更新绘图界面，显示新的曲线形状。
确保整个过程的响应速度足够快，以实现流畅的用户体验。

为了实现高效更新，可以采用以下策略：

预计算和缓存 ：预先计算可能会用到的值，并将它们存储在缓存中，从而减少实时计算负担。
分层渲染 ：将曲线的绘制分解为多个层次，先绘制底层，再绘制上层，可以优化渲染效率。
双缓冲技术 ：使用两个缓冲区，一个用于绘制，一个用于显示，可以避免在绘制过程中产生闪烁。

下面是使用HTML5 Canvas和JavaScript来动态调整Bezier曲线控制点并实时更新的简单示例代码：

// HTML部分
<canvas id="myCanvas" width="400" height="400"></canvas>// JavaScript部分
const canvas = document.getElementById('myCanvas');
const ctx = canvas.getContext('2d');// 初始化控制点
let controlPoints = [{x: 50, y: 200}, {x: 150, y: 100}, {x: 250, y: 300}, {x: 350, y: 200}];// 绘制Bezier曲线的函数
function drawBezier() {ctx.beginPath();ctx.moveTo(controlPoints[0].x, controlPoints[0].y);for (let i = 1; i < controlPoints.length; i++) {ctx.bezierCurveTo(controlPoints[i].x, controlPoints[i].y,controlPoints[i].x, controlPoints[i].y,controlPoints[i].x, controlPoints[i].y);}ctx.stroke();
}// 更新控制点位置的函数
function updateControlPoints(x, y, index) {controlPoints[index] = {x: x, y: y};drawBezier();
}// 为每个控制点添加事件监听器
for (let i = 0; i < controlPoints.length; i++) {let cp = controlPoints[i];canvas.addEventListener('mousemove', (event) => {let rect = canvas.getBoundingClientRect();let mouseX = event.clientX - rect.left;let mouseY = event.clientY - rect.top;updateControlPoints(mouseX, mouseY, i);});
}// 首次绘制曲线
drawBezier();

这段代码首先初始化了一个Canvas，并在其中绘制了初始的Bezier曲线。每个控制点在页面上用一个可拖动的点表示。当用户拖动这些点时，会触发事件监听器，进而调用 updateControlPoints 函数更新控制点位置并重新绘制曲线。这是一个简单的交互示例，展示了如何将用户输入与Bezier曲线的动态调整结合起来。

5. Bezier曲线在图形设计、游戏开发、CAD系统等领域的应用案例

5.1 Bezier曲线在图形设计中的应用

5.1.1 设计软件中的曲线工具

在图形设计中，Bezier曲线是一个不可或缺的工具。许多流行的设计软件，如Adobe Illustrator、CorelDRAW以及Affinity Designer等，都内置了强大的Bezier曲线编辑功能。设计师通过调整控制点来精确地创建平滑的曲线和复杂图形，Beizer曲线的应用使得图形设计更加灵活和高效。