目录
一.求链式二叉树节点个数
二.求链式二叉树叶子节点个数
三.求链式二叉树第k层节点个数
四.求链式二叉树的深度/高度
五.链式二叉树查找值为x的节点
六.链式二叉树的销毁
七. 测试函数
八. 总结:
前言:
在学习链式二叉树的常用操作之前 我们需要手动创建一个二叉树 在上文的学习中 我们已经学习过了 链式二叉树的创建 代码如下
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>// 二叉树节点结构定义
typedef char BTDataType;
typedef struct BinaryTreeNode {BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
} BTNode;// 创建新节点
BTNode* BuyBTNode(BTDataType x) {BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL) {printf("malloc failed\n");exit(-1);}node->data = x;node->left = NULL;node->right = NULL;return node;
}// 构建示例二叉树(便于测试)
BTNode* CreateBinaryTree() {BTNode* nodeA = BuyBTNode('A');BTNode* nodeB = BuyBTNode('B');BTNode* nodeC = BuyBTNode('C');BTNode* nodeD = BuyBTNode('D');BTNode* nodeE = BuyBTNode('E');BTNode* nodeF = BuyBTNode('F');nodeA->left = nodeB;nodeA->right = nodeC;nodeB->left = nodeD;nodeC->right = nodeE;nodeC->left = nodeF;return nodeA;
}一.求链式二叉树节点个数
代码实现:
// 一、求二叉树节点个数
int BinaryTreeSize(BTNode* root) {// 空树节点个数为0return root == NULL ? 0 : 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}
- 功能:计算二叉树中所有节点的总数。
- 实现思路:
- 空树(
root == NULL)返回 0; - 非空树则返回「1(当前节点)+ 左子树节点数 + 右子树节点数」;
- 递归遍历整个树,累加所有节点。
- 空树(
- 时间复杂度:O (n),需访问每个节点一次。
二.求链式二叉树叶子节点个数
代码实现:
// 二、求二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root) {// 空树叶子节点个数为0if (root == NULL) {return 0;}// 左右孩子都为空的节点是叶子节点if (root->left == NULL && root->right == NULL) {return 1;}// 递归计算左右子树的叶子节点总和return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}- 功能:统计二叉树中叶子节点(无左右子树的节点)的数量。
- 实现思路:
- 空树返回 0;
- 若当前节点的左右指针均为
NULL,则是叶子节点,返回 1; - 否则递归计算左子树和右子树的叶子节点之和。
三.求链式二叉树第k层节点个数
代码实现:
// 三、求二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k) {assert(k >= 1); // k必须是正整数// 空树或k小于1,返回0if (root == NULL) {return 0;}// 第1层只有根节点if (k == 1) {return 1;}// 第k层节点个数 = 左子树第k-1层节点数 + 右子树第k-1层节点数return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}- 功能:计算二叉树中第 k 层(根节点为第 1 层)的节点总数。
- 实现思路:
- 边界检查:
k < 1时断言报错,空树返回 0; - 递归降层:第 k 层节点数等价于左右子树第 k-1 层节点数之和;
- 终止条件:
k == 1时,当前节点即为第 1 层节点,返回 1。
- 边界检查:
- 注意:若 k 大于树的深度,返回 0。
四.求链式二叉树的深度/高度
代码实现:
// 四、求二叉树的深度/高度
int BinaryTreeDepth(BTNode* root) {// 空树深度为0if (root == NULL) {return 0;}// 计算左右子树深度int leftDepth = BinaryTreeDepth(root->left);int rightDepth = BinaryTreeDepth(root->right);// 树的深度 = 左右子树最大深度 + 1(当前节点)return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}- 功能:计算二叉树的最大深度(从根节点到最远叶子节点的层数)。
- 实现思路:
- 空树深度为 0;
- 递归计算左子树和右子树的深度;
- 当前树的深度 = 左右子树中最大深度 + 1(当前节点所在层)。
- 特点:体现了「分治思想」,将树的深度问题分解为子树的深度问题。
五.链式二叉树查找值为x的节点
代码实现:
// 五、二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x) {// 空树返回NULLif (root == NULL) {return NULL;}// 找到目标节点,返回该节点指针if (root->data == x) {return root;}// 先在左子树查找BTNode* leftRet = BinaryTreeFind(root->left, x);if (leftRet != NULL) {return leftRet;}// 左子树没找到,再在右子树查找BTNode* rightRet = BinaryTreeFind(root->right, x);return rightRet;
}- 功能:在二叉树中查找值为 x 的节点,返回该节点的指针(若不存在返回
NULL)。 - 实现思路:
- 空树返回
NULL; - 先检查当前节点是否为目标节点,是则返回;
- 否则先递归查找左子树,找到则返回;
- 左子树未找到时,递归查找右子树并返回结果。
- 空树返回
- 查找顺序:本质是「前序遍历查找」,先根节点,再左子树,最后右子树。
六.链式二叉树的销毁
代码实现:
// 六、二叉树的销毁
void BinaryTreeDestroy(BTNode** root) {// 空树直接返回if (*root == NULL) {return;}// 先销毁左子树BinaryTreeDestroy(&(*root)->left);// 再销毁右子树BinaryTreeDestroy(&(*root)->right);// 最后释放当前节点free(*root);*root = NULL; // 避免野指针
}
- 功能:释放二叉树所有节点的内存,彻底销毁树结构。
- 实现思路:
- 采用「后序遍历」思路:先销毁左子树,再销毁右子树,最后释放当前节点;
- 使用二级指针
**root,确保销毁后根节点被置为NULL,避免野指针; - 递归释放所有节点,无内存泄漏。
- 关键:必须先释放子树,再释放当前节点,否则会丢失子树指针导致内存泄漏。
七. 测试函数
//测试函数
int main() {BTNode* root = CreateBinaryTree();// 测试节点个数printf("二叉树节点总数: %d\n", BinaryTreeSize(root));// 测试叶子节点个数printf("二叉树叶子节点个数: %d\n", BinaryTreeLeafSize(root));// 测试第k层节点个数printf("第2层节点个数: %d\n", BinaryTreeLevelKSize(root, 2));printf("第3层节点个数: %d\n", BinaryTreeLevelKSize(root, 3));// 测试树的深度printf("二叉树深度: %d\n", BinaryTreeDepth(root));// 测试查找节点BTNode* findNode = BinaryTreeFind(root, 'E');if (findNode != NULL) {printf("找到节点: %c\n", findNode->data);}else {printf("未找到节点\n");}// 销毁二叉树BinaryTreeDestroy(&root);assert(root == NULL); // 验证树已被销毁return 0;
}代码运行结果如下:
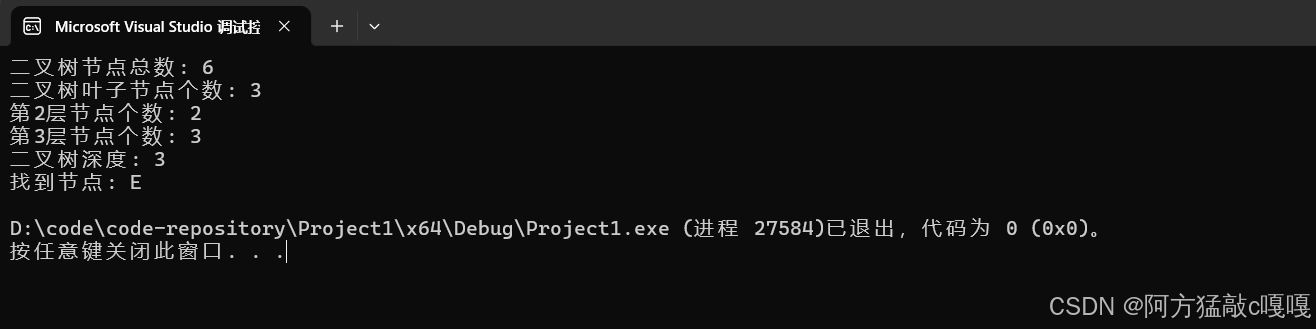
链式二叉树如下图 进行验证
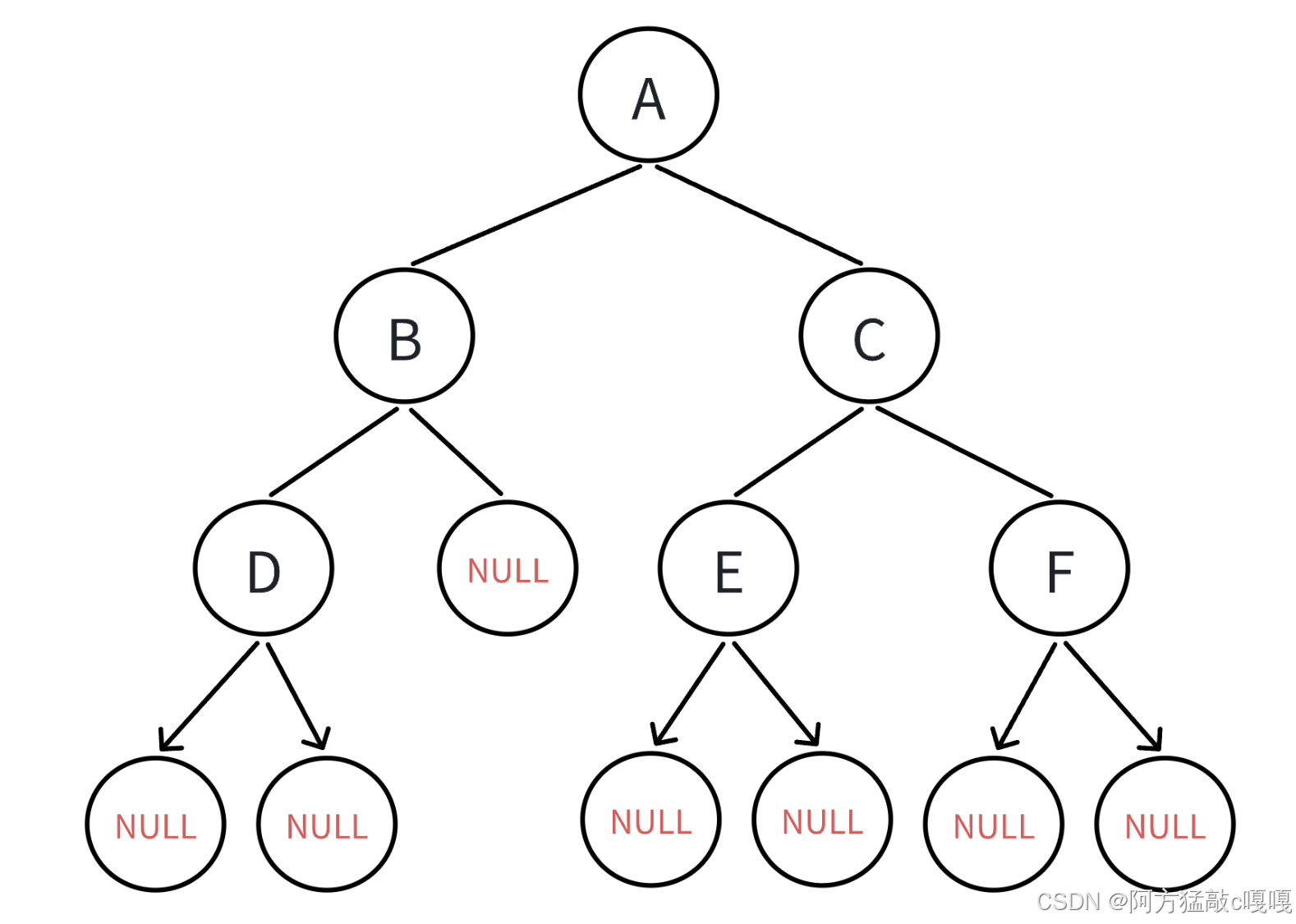
根据上图 不难得出 代码运行 正确
八. 总结:
所有函数均采用递归实现,符合二叉树的递归特性(每个节点的左、右子树仍是二叉树)。核心思想是「分治」:将对整棵树的操作分解为对根节点和左右子树的操作,简化问题复杂度。每个函数的时间复杂度均为 O (n)(n 为节点总数),空间复杂度为 O (h)(h 为树的高度,递归栈的深度)。


)





)

)
)



)



——以“数据”驱动电机实现真正的无模型)