在C++算法与数据结构领域，前缀和是一种时间复杂度优化利器，尤其适用于频繁查询数组区间和的场景。它通过预先计算“前缀累积和”，将原本O(n)时间的区间和查询压缩至O(1)，是面试、竞赛及工程开发中高频使用的基础技巧。

一、前缀和的核心原理

1.1 定义：什么是前缀和？

前缀和（Prefix Sum）本质是一个辅助数组，其中每个元素的值等于原数组从“起始位置”到“当前位置”的所有元素之和。对于一维数组，我们通常将前缀和数组定义为pre，其数学表达式如下：

设原数组为a[1...n]（注：实际开发中常将数组下标从1开始，避免处理边界0时的逻辑判断），前缀和数组pre[0...n]的定义为：

pre[0] = 0（哨兵位，用于简化计算）
pre[i] = a[1] + a[2] + ... + a[i]（即前i个元素的累积和）

例如，原数组a = [1, 2, 3, 4, 5]，其前缀和数组pre计算过程如下：

pre[0] = 0（哨兵）
pre[1] = a[1] = 1
pre[2] = a[1] + a[2] = 1 + 2 = 3
pre[3] = a[1] + a[2] + a[3] = 1 + 2 + 3 = 6
pre[4] = 1 + 2 + 3 + 4 = 10
pre[5] = 1 + 2 + 3 + 4 + 5 = 15

最终pre = [0, 1, 3, 6, 10, 15]。

1.2 核心价值：区间和的O(1)查询

前缀和的核心作用是快速计算原数组任意区间[l, r]的和。根据前缀和的定义，区间和sum(l, r)（即a[l] + a[l+1] + ... + a[r]）可通过前缀和数组推导得出：

sum(l, r) = pre[r] - pre[l-1]

推导过程：

pre[r] = a[1] + a[2] + ... + a[l-1] + a[l] + ... + a[r]
pre[l-1] = a[1] + a[2] + ... + a[l-1]
两者相减后，前l-1个元素的和被抵消，剩余部分恰好是a[l]到a[r]的和。

以上述a = [1,2,3,4,5]为例，若查询区间[2,4]（即2+3+4=9）：

pre[4] = 10，pre[1] = 1
sum(2,4) = pre[4] - pre[1] = 10 - 1 = 9，结果完全正确。

1.3 时间与空间复杂度分析

前缀和的优势体现在“预处理+多次查询”的场景中，其复杂度如下：

预处理阶段：遍历原数组一次，计算前缀和数组，时间复杂度为O(n)（n为原数组长度）；
查询阶段：每次查询仅需一次减法运算，时间复杂度为O(1)，无论查询多少次，总查询时间仅为O(q)（q为查询次数）；
空间复杂度：需额外存储长度为n+1的前缀和数组，空间复杂度为O(n)（可优化为原地存储，见下文“优化技巧”）。

对比“暴力查询”（每次查询遍历区间[l, r]，时间复杂度O(n*q)），当查询次数q较大时（如q>1000），前缀和的效率优势会呈指数级放大。

二、一维前缀和的C++实现

一维前缀和是基础，其实现流程分为“预处理前缀和数组”和“处理区间查询”两步，以下通过完整代码示例讲解。

2.1 基础实现（下标从1开始）

下标从1开始是最常用的方式，通过pre[0] = 0的哨兵位，避免处理l=1时l-1=0的边界判断错误。

#include <iostream>
#include <vector>
using namespace std;int main() {// 1. 输入原数组（长度n）int n, q; // n：原数组长度，q：查询次数cin >> n >> q;vector<int> a(n + 1); // 原数组：a[1]~a[n]for (int i = 1; i <= n; ++i) {cin >> a[i];}// 2. 预处理前缀和数组prevector<int> pre(n + 1, 0); // pre[0] = 0，pre[1]~pre[n]为前缀和for (int i = 1; i <= n; ++i) {pre[i] = pre[i - 1] + a[i]; // 递推公式：当前前缀和 = 前一个前缀和 + 原数组当前元素}// 3. 处理q次区间查询while (q--) {int l, r; // 查询区间[l, r]cin >> l >> r;// 计算区间和并输出int sum = pre[r] - pre[l - 1];cout << "区间[" << l << "," << r << "]的和为：" << sum << endl;}return 0;
}

输入输出示例：

输入：
5 3  // 原数组长度5，查询3次
1 2 3 4 5  // 原数组a[1]~a[5]
1 3  // 查询[1,3]
2 4  // 查询[2,4]
3 5  // 查询[3,5]输出：
区间[1,3]的和为：6
区间[2,4]的和为：9
区间[3,5]的和为：12

2.2 优化技巧：原地存储前缀和

若原数组后续无需使用，可直接在原数组上存储前缀和，省去额外的pre数组，将空间复杂度从O(n)优化为O(1)（不考虑输入数组本身的空间）。

实现代码如下：

#include <iostream>
#include <vector>
using namespace std;int main() {int n, q;cin >> n >> q;vector<int> a(n + 1); // 原数组与前缀和数组共用for (int i = 1; i <= n; ++i) {cin >> a[i];a[i] += a[i - 1]; // 原地更新：a[i]变为前i个元素的前缀和}while (q--) {int l, r;cin >> l >> r;cout << a[r] - a[l - 1] << endl;}return 0;
}

注意事项：

此优化仅适用于“原数组无需保留”的场景（如仅需查询区间和，后续不操作原数组）；
若原数组需后续使用（如修改元素后重新计算前缀和），则不可使用原地存储。

2.3 边界问题处理

前缀和的边界错误是新手常见问题，需重点关注以下两点：

下标从0开始的情况：若原数组下标从0开始（如a[0]~a[n-1]），前缀和数组pre[0] = 0，pre[i] = a[0] + ... + a[i-1]，此时区间[l, r]（0-based）的和为pre[r+1] - pre[l]。示例代码如下：

vector<int> a = {1,2,3,4,5};
int n = a.size();
vector<int> pre(n + 1, 0);
for (int i = 1; i <= n; ++i) {pre[i] = pre[i-1] + a[i-1]; // a[i-1]是原数组第i个元素
}
// 查询区间[1,3]（0-based，即2+3+4）
int l = 1, r = 3;
int sum = pre[r+1] - pre[l]; // pre[4]-pre[1] = 10-1=9

数据溢出问题：若原数组元素为int类型且数值较大（如a[i]为1e9，n为1e5），前缀和可能超过int的最大值（2^31-1 ≈ 2e9），此时需将前缀和数组类型改为long long。示例：
```
vector<long long> pre(n + 1, 0); // 用long long避免溢出
for (int i = 1; i <= n; ++i) {pre[i] = pre[i-1] + a[i]; // a[i]若为int，会自动提升为long long
}
```

三、二维前缀和：处理矩阵区间和

一维前缀和的思想可扩展到二维场景，用于快速计算矩阵中任意子矩阵的元素和（如查询(x1,y1)到(x2,y2)构成的子矩阵和），是图像处理、矩阵分析等领域的常用技巧。

3.1 二维前缀和的定义与推导

设原矩阵为a[1...n][1...m]（下标从1开始），二维前缀和数组pre[0...n][0...m]的定义为：

pre[i][j]表示以(1,1)为左上角、(i,j)为右下角的子矩阵的所有元素之和。

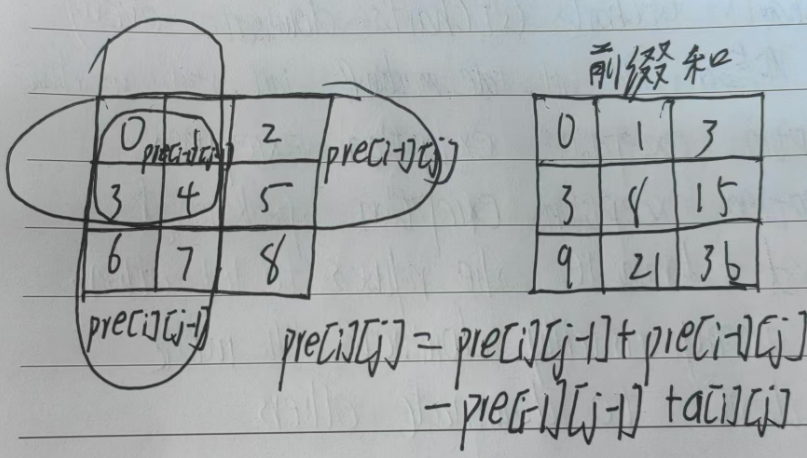
在这里插入图片描述

递推公式推导：

要计算pre[i][j]，需考虑以下四部分：

左上角子矩阵(1,1)-(i-1,j-1)的和：pre[i-1][j-1]；
左边子矩阵(1,j)-(i-1,j)的和：pre[i-1][j] - pre[i-1][j-1]；
上边子矩阵(i,1)-(i,j-1)的和：pre[i][j-1] - pre[i-1][j-1]；
当前元素a[i][j]。

合并后得到递推公式：

pre[i][j] = pre[i-1][j] + pre[i][j-1] - pre[i-1][j-1] + a[i][j]

子矩阵和计算：

对于任意子矩阵(x1,y1)-(x2,y2)（左上角为(x1,y1)，右下角为(x2,y2)），其和sum的公式为：

sum = pre[x2][y2] - pre[x1-1][y2] - pre[x2][y1-1] + pre[x1-1][y1-1]

推导逻辑：用pre[x2][y2]（大矩阵和）减去“上方无关区域”（pre[x1-1][y2]）和“左方无关区域”（pre[x2][y1-1]），但此时“左上角重叠区域”（pre[x1-1][y1-1]）被多减了一次，需加回。

3.2 二维前缀和的C++实现

以下代码实现“输入一个n行m列的矩阵，处理q次子矩阵和查询”：

#include <iostream>
#include <vector>
using namespace std;int main() {int n, m, q; // n：行数，m：列数，q：查询次数cin >> n >> m >> q;// 1. 输入原矩阵（下标1开始）vector<vector<int>> a(n + 1, vector<int>(m + 1));for (int i = 1; i <= n; ++i) {for (int j = 1; j <= m; ++j) {cin >> a[i][j];}}// 2. 预处理二维前缀和数组vector<vector<long long>> pre(n + 1, vector<long long>(m + 1, 0));for (int i = 1; i <= n; ++i) {for (int j = 1; j <= m; ++j) {pre[i][j] = pre[i-1][j] + pre[i][j-1] - pre[i-1][j-1] + a[i][j];}}// 3. 处理q次查询while (q--) {int x1, y1, x2, y2; // 子矩阵的左上角(x1,y1)和右下角(x2,y2)cin >> x1 >> y1 >> x2 >> y2;// 计算子矩阵和long long sum = pre[x2][y2] - pre[x1-1][y2] - pre[x2][y1-1] + pre[x1-1][y1-1];cout << "子矩阵(" << x1 << "," << y1 << ")-(" << x2 << "," << y2 << ")的和为：" << sum << endl;}return 0;
}

输入输出示例：

输入：
3 3 2  // 3行3列矩阵，2次查询
1 2 3  // 第1行
4 5 6  // 第2行
7 8 9  // 第3行
1 1 2 2  // 查询子矩阵(1,1)-(2,2)（1+2+4+5=12）
2 3 3 3  // 查询子矩阵(2,3)-(3,3)（6+9=15）输出：
子矩阵(1,1)-(2,2)的和为：12
子矩阵(2,3)-(3,3)的和为：15

四、前缀和的实战应用场景

前缀和并非孤立的技巧，而是许多复杂算法的基础组件，以下列举典型应用场景。

4.1 场景1：统计区间和等于k的子数组个数

问题描述：给定一个整数数组a和整数k，统计所有和为k的连续子数组的个数（LeetCode 560. Subarray Sum Equals K）。

前缀和思路：

设前缀和数组为pre，则子数组[i+1, j]的和为pre[j] - pre[i]；
若pre[j] - pre[i] = k，则pre[i] = pre[j] - k；
遍历数组时，用哈希表（unordered_map）存储每个pre[i]出现的次数，对于当前pre[j]，查询哈希表中pre[j]-k的出现次数，累加至结果。

C++实现代码：

#include <iostream>
#include <vector>
#include <unordered_map>
using namespace std;int subarraySum(vector<int>& nums, int k) {unordered_map<long long, int> preCount; // key：前缀和，value：出现次数preCount[0] = 1; // 初始化：pre[0] = 0出现1次long long pre = 0; // 当前前缀和int res = 0;for (int num : nums) {pre += num; // 更新当前前缀和// 若pre - k存在，说明有pre[i] = pre[j] - k，对应子数组和为kif (preCount.find(pre - k) != preCount.end()) {res += preCount[pre - k];}preCount[pre]++; // 记录当前前缀和的出现次数}return res;
}int main() {vector<int> nums = {1, 1, 1};int k = 2;cout << "和为" << k << "的子数组个数：" << subarraySum(nums, k) << endl; // 输出2return 0;
}