重点内容:
函数:
定义:
返回值类型 函数名(参数列表) { //函数体 }
函数的参数列表中可以有多个数据
返回值:如果函数没有返回值可以写成void 返回值的作用,函数的结果用来返回给主调函数的,如果主调函数处不需要函数的结果,函数可以没有返回值
参数:如果函数实现功能时,需要外部传递数据过来,那么函数就需要参数
写在函数定义位置的参数叫做形式参数,没有实际的意义,只起到占位作用
函数的定义不能嵌套
函数的分类:
是否需要自己定义:库函数、自定义函数
是否被调用的角度:主调函数、被调函数
是否有返回值和参数的角度:
1.有参有返回值
2.有参无返回值
3.无参无返回值
4.无参有返回值
函数的调用:
函数名(实际参数);
实际参数的个数需要和形式参数的个数保持一致
函数调用的过程就是实参初始化形参的过程
函数定义的代码不会执行,只有函数被调用时才会执行函数体
不同函数中的同名变量,互不相关
函数的返回值:
函数的返回值可以理解为函数调用的结果
函数声明:
函数定义在函数调用下方时,需要函数声明
格式: 返回值类型 函数名(参数类型);
作用: 告诉编译器,函数的参数类型和返回值类型,让编译器可以找到该函数
数组作为函数参数传递:
所有出现在函数形参位置长得像数组定义的代码,实际上都是指针
void fun(int *p,int len) //一维整形数组:形参需要使用同类型的指针变量接收一维整形数组的地址,还需要传一维整型数组的长度(因为在功能函数中不能求出数组的长度)
void fun(char *p)//一维字符数组:只需要接收一维字符数组的首地址即可,不需要接收长度
void fun(int (*p)[3],int r,int c)//二维数组作为函数参数传递时,形参需要使用数组指针接收
指针函数:
全局变量和局部变量:
全局变量:不定义在任何括号中的变量,生命周期和作用域是程序的开始到结束
局部变量:定义在括号中的变量,生命周期和作用域是括号的开始到结束
如何区分生命周期和作用域:
生命周期:内存存在的时候
作用域:可以访问的位置
static的使用:
static用于局部变量:延长局部变量的生命周期,编程程序的开始到结束
static修饰全局变量:不能在其他文件中访问该全局变量
static修饰函数:不能在其他文件中调用函数
指针函数:
本质是一个函数,返回值是指针(一定是一个有返回值的函数)
返回值是函数返回到主调函数处的结果
总结:指针函数可以返回生命周期更长的变量的地址
动态内存分配:
申请堆区内存
malloc:
void *malloc(size_t size);
功能:从堆区申请指定字节数的空间
返回值:申请的堆区空间的首地址
参数:申请多少个Byte
free:
void free(void *ptr);
功能:释放堆区内存
返回值:无
参数:万能指针,接收任意类型的地址(要释放空间的首地址)
内存泄漏:
堆区有空间没有在使用,但是空间所有权没有还给内存,导致无法从堆区申请空间,这种情况叫内存泄漏
如何避免内存泄漏,申请空间之后记得释放
函数指针:
本质是一个指针,指向一个函数
int add(int a,int b) { return a+b; } -->int (*p)(int,int) = add;//返回值类型 (*函数指针名)(形参类型); 让指针指向指定返回值类型和参数类型的函数
回调函数:
函数的其中一个参数是函数指针,由函数指针指向的函数来完成实际的功能
递归函数:
递归的三要素:
递归出口(没有就是死递归)
递归逻辑
递归返回值
作业:
1.赶鸭子问题:一个人赶着鸭子去村庄卖,每经过一个村子卖出一半又一只,经过七个村庄后还剩下两只鸭子,问出发时共赶了多少只鸭子
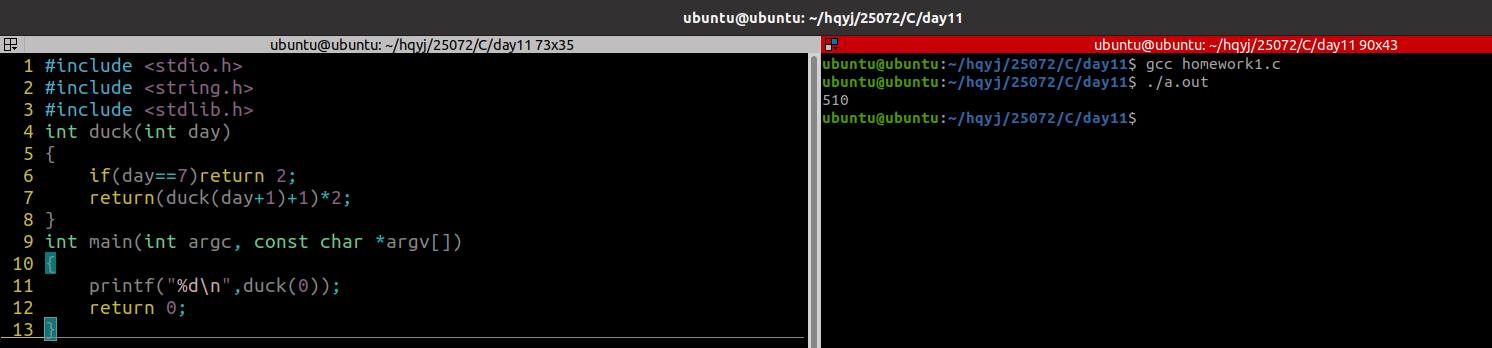
程序源码:
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
int duck(int day)
{
if(day==7)return 2;
return(duck(day+1)+1)*2;
}
int main(int argc, const char *argv[])
{
printf("%d\n",duck(0));
return 0;
}
2.用递归输出数的二进制
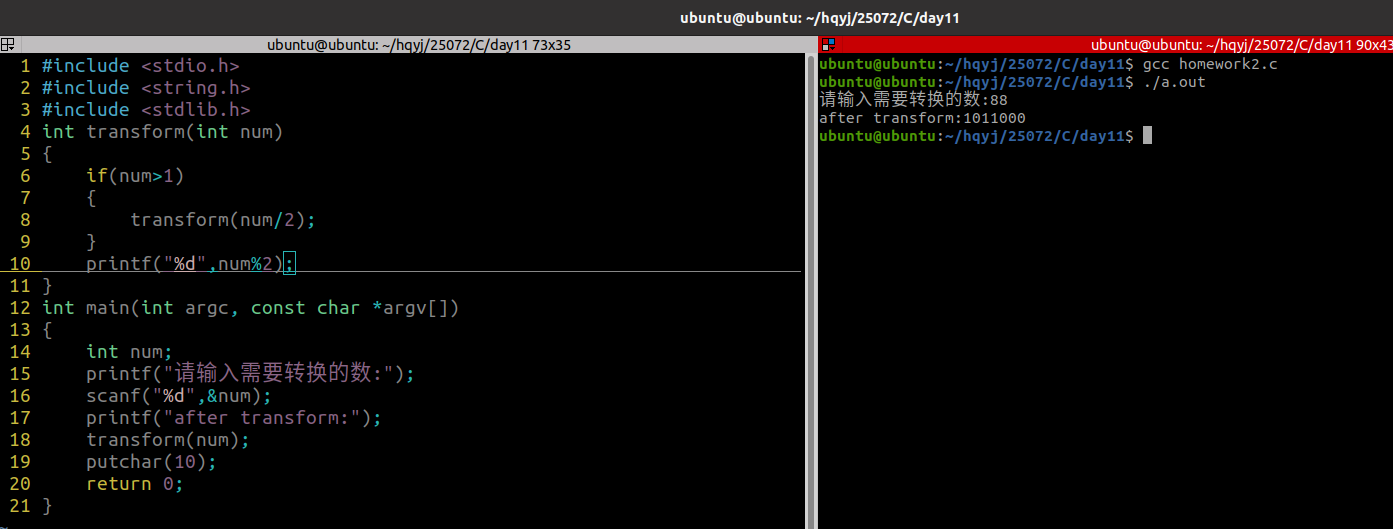
程序源码:
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
int transform(int num)
{
if(num>1)
{
transform(num/2);
}
printf("%d",num%2);
}
int main(int argc, const char *argv[])
{
int num;
printf("请输入需要转换的数:");
scanf("%d",&num);
printf("after transform:");
transform(num);
putchar(10);
return 0;
}
3.递归输出斐波那契数列
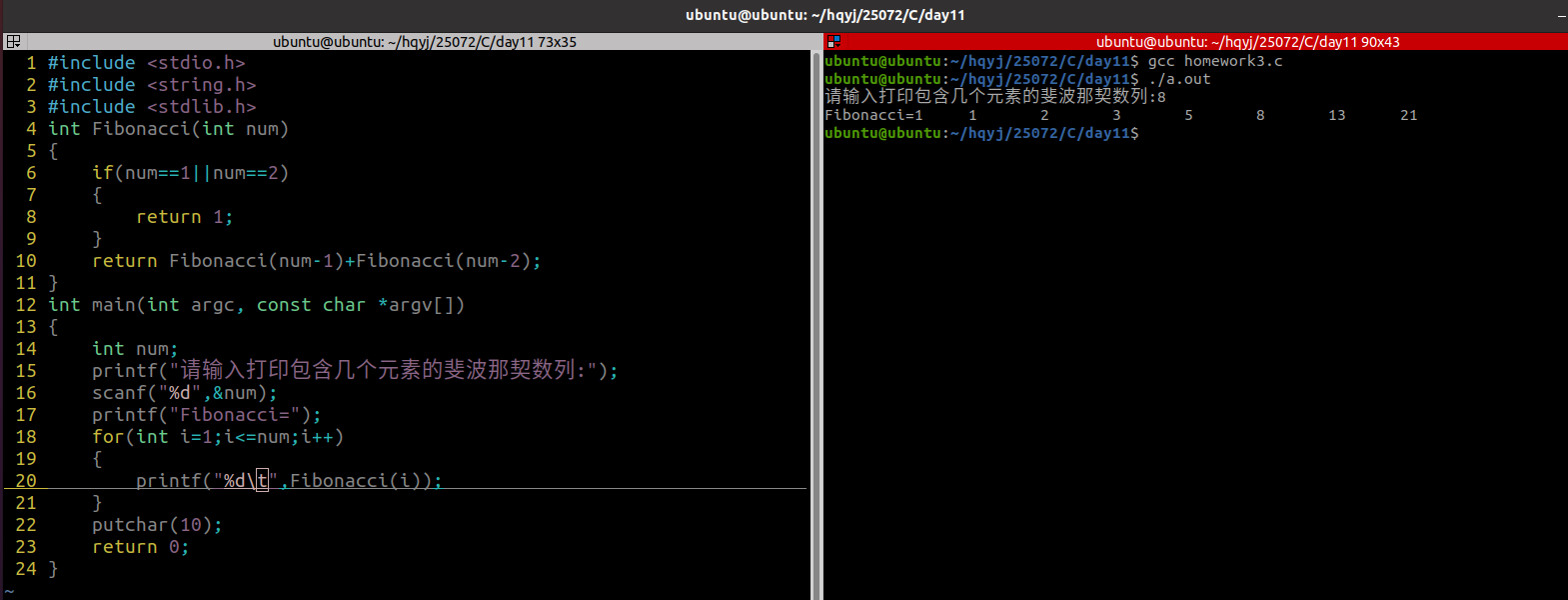
程序源码:
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
int Fibonacci(int num)
{
if(num==1||num==2)
{
return 1;
}
return Fibonacci(num-1)+Fibonacci(num-2);
}
int main(int argc, const char *argv[])
{
int num;
printf("请输入打印包含几个元素的斐波那契数列:");
scanf("%d",&num);
printf("Fibonacci=");
for(int i=1;i<=num;i++)
{
printf("%d\t",Fibonacci(i));
}
putchar(10);
return 0;
}
4.整理思维导图

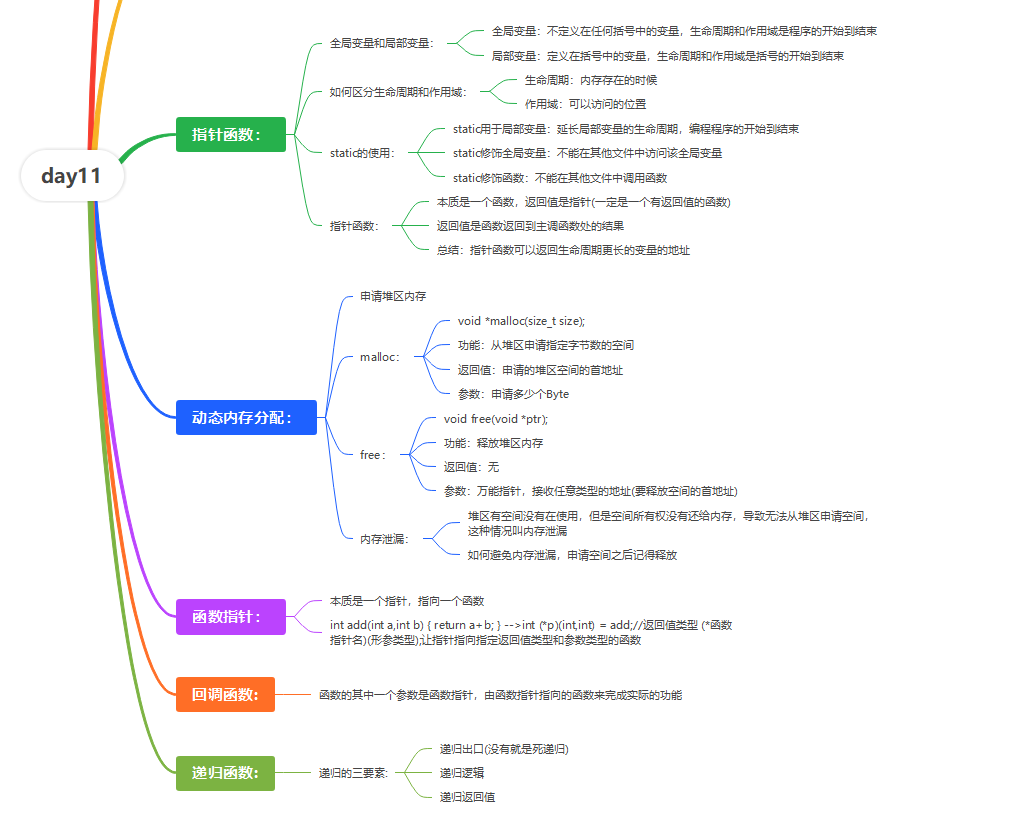
——VLN的数据集和评估方法 3.2)


--Java版)



排序算法——归并排序)





)



![[已解决]当启动 Spring Boot 应用时出现 Using generated security password xxx提示](http://pic.xiahunao.cn/[已解决]当启动 Spring Boot 应用时出现 Using generated security password xxx提示)

,用例图,类图,活动图,序列图,状态图,实体关系图(ERD),BPMN(业务流程建模)详解分析)