决策树构建：

决策树的结构与python中的二叉树结构(PY数据结构-树)相似，不过决策树中除了叶节点之外的其他节点，都被称之为“决策节点”，构建决策树的过程，也就是选取每一个节点采用哪一个特征作为划分依据的过程。

以解决二元分类问题为例，最终的叶节点输出只有两种情况：0或1，那么在前面的每一个决策节点时我们自然希望每一个节点分支得到的样本尽可能属于同一个类别，也就是说得到的示例样本纯度最高。因此，我们引入“熵”的概念，熵用于衡量样本的不纯度，其表达式如下：

其中： ——所有样本中正例的占比；

            ——所有样本中负例的占比。

其图像如上图所示，可以看出，当一个样本中正例和负例各占一半时，对于分类而言此时样本是最不纯的，相应的熵值取最大值1；而当一个样本中全部为正例或负例时，对于分类而言此时样本最纯，相应的熵值取最小值0。

因此，决策节点的特征选取问题就转变为哪一个特征作为划分依据时可以最大程度的降低熵值的问题。并且，需要注意的一点是，当某一个分支的样本的数量较大时，保证该分支的纯度是更为重要的。这是因为样本数量多的分支在训练数据中占比更高，其分类结果对模型的整体准确率、召回率等指标影响更大。因此我们进一步的将特征分裂后的左右子分支得到的熵值进行加权平均计算：

熵值的减少量也被称之为信息增益，而在实际运用中，我们一般会采取最大信息增益（也就是最大熵值降低）作为划分依据，这与树的停止划分有关。信息增益计算如下：

划分停止依据：

决策树的停止划分依据有如下四种：

• 该节点已经100%是某一个类别；
• 已经达到的树的最大深度；
• 信息增益已经低于阈值；
• 节点的示例样本已经低于阈值。

即使最终树的叶节点没有达到100%的纯度，我们也需要通过其他依据来停止继续划分，因为当树的规模过大时难以管理，并且很有可能会出现过拟合（决策树会为了纯度不断地生成过于复杂的划分规则）。同时，当继续划分得到的信息增益过小时，也没有必要再继续进行下去，理由同前者。

特征取值非二元：

前面提到过决策树的结构与二叉树相似，而如果某一个特征的取值是>2个的离散值/连续任意值时，我们需要采用一些转换的方法来保证二叉的结构。

独热编码：

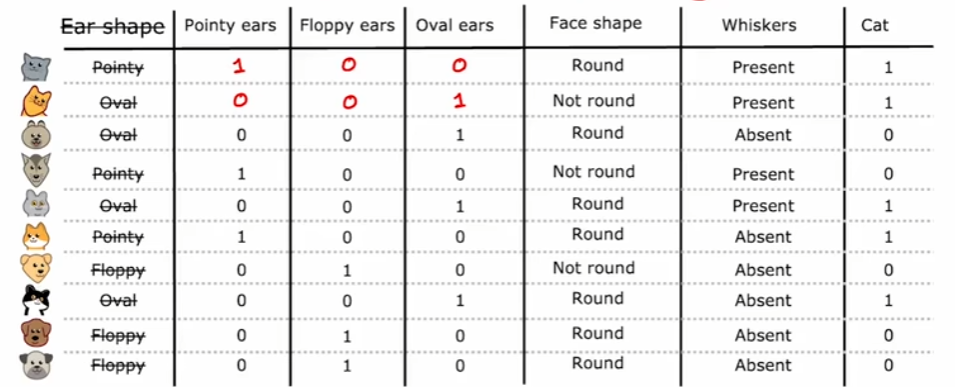
对于取值为非任意离散值时，比如在下图的耳朵形状特征的取值中，可取值有三类：尖耳、垂耳以及椭圆形，我们将耳朵形状的分类变量转换成二进制向量，如下图所示。此时我们不再将耳朵形状作为分类特征，而是直接将它的三个取值类别作为分类特征，相应的每个样本在这三个分类特征中只会有一个值取1，因此称为独热。

阈值分割：

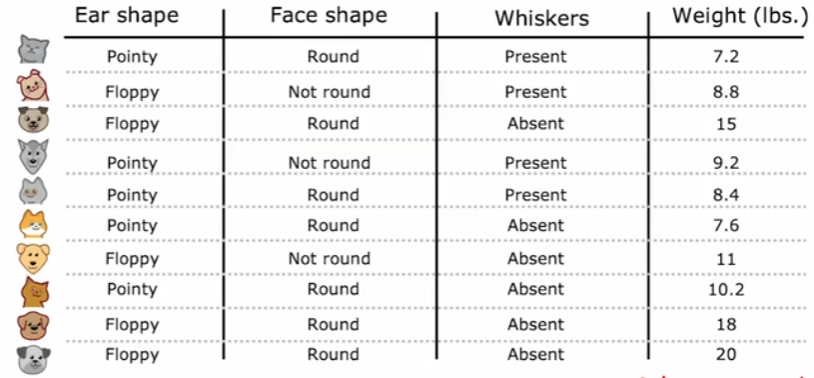
对于取值为连续任意值时，比如下图中的体重，此时无法同上采用独热编码来处理，因此一般是通过阈值分割将此特征的取值划分为两类作为分裂。而对于阈值的选择，通常是将训练样本中所有该特征取值进行排序，再取相邻值的中点作为候选阈值，然后计算每个候选阈值分裂后的信息增益，选择使增益最大的阈值。这可以保证在所有训练数据中确保找到当前特征下的全局最优分裂点，不过相应的计算成本较高。

回归树：

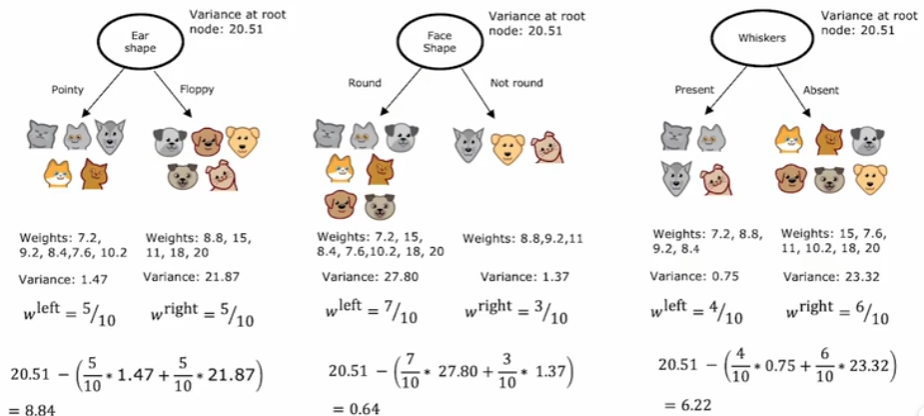
前面提到的决策树都是解决分类问题，不过决策树也可以推广到解决回归问题，也就是创建回归树。同样还是上图，此时我们不再把最右侧的体重作为输入特征，而是直接作为输出，问题就转变为了对于体重的预测。同样是选取不同的输入特征作为决策节点，现在我们要计算的不再是信息增益，之前目标是保证叶节点中的样本更多的为一个类别，此时目标则是保证叶结点中的样本体重尽可能接近，因为最终叶结点中所有样本的体重均值将作为此叶结点的预测结果。所以，每一次选择节点时，需要计算的是划分后的方差减少量，能够最大化降低方差的就作为当前决策节点。