自动驾驶中的坐标系概念及相互间的转换公式推导

在自动驾驶系统中，多个坐标系用于描述车辆、传感器和环境的相对位置。这些坐标系之间的转换是实现定位、感知和控制的关键。下面我将逐步解释常见坐标系的概念，并推导相互转换的公式。推导基于标准几何变换和齐次坐标表示，确保公式正确可靠。

一、坐标系概念

在自动驾驶中，主要涉及以下坐标系：

1. 世界坐标系（World Coordinate System）：全局坐标系，固定在地球上（如基于GPS或地图），原点通常为固定参考点（如起点）。用于描述车辆和环境在全局中的位置。
2. 车辆坐标系（Vehicle Coordinate System）：以车辆为中心，原点通常在车辆重心或后轴中心。$x$轴指向车辆前进方向，$y$轴指向左侧，$z$轴向上。用于描述车辆自身状态。
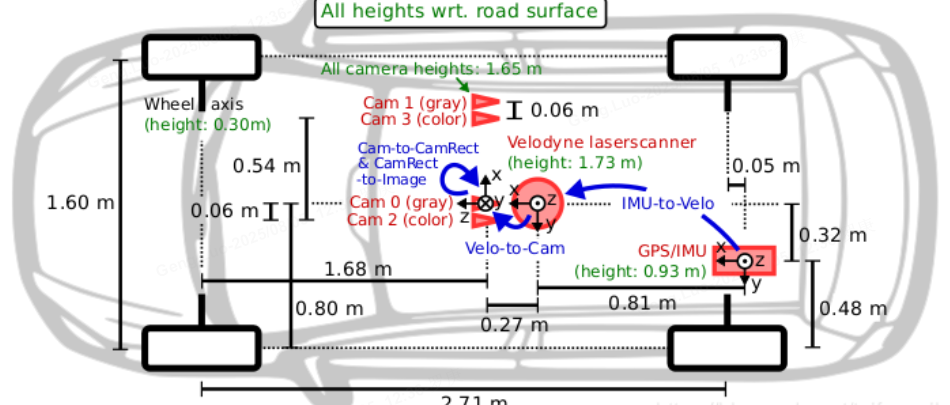
3. 传感器坐标系（Sensor Coordinate System）：以传感器（如激光雷达、摄像头）为中心，原点在传感器安装点。每个传感器有自己的坐标系，用于描述传感器测量数据。
4. 相机坐标系（Camera Coordinate System）：针对摄像头，原点在相机光心，$z$轴沿光轴方向，$x$轴和$y$轴平行于图像平面。用于描述点在相机空间的位置。
5. 像素坐标系（Pixel Coordinate System）：针对图像传感器，原点在图像左上角，$u$轴向右，$v$轴向下。用于描述像素位置。

这些坐标系相互关联，需要通过旋转和平移进行转换。转换通常使用齐次坐标（Homogeneous Coordinates）来表示，以简化矩阵运算。齐次坐标形式为 $\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$。

二、坐标系转换公式推导

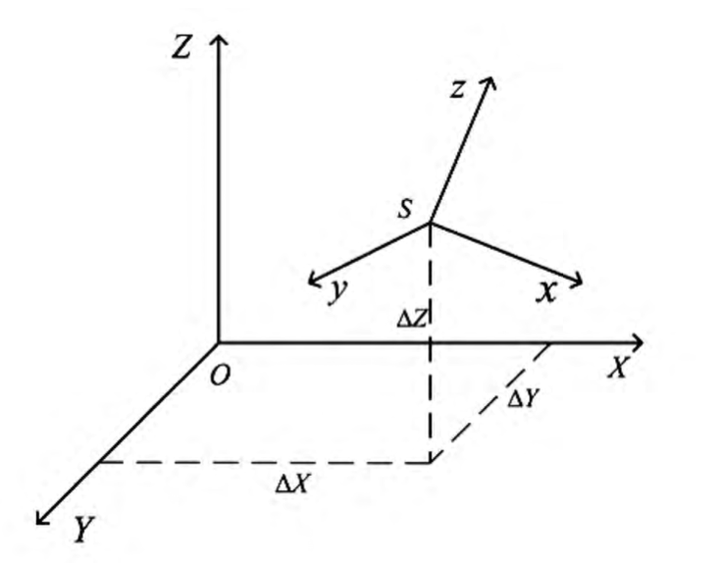
转换公式推导基于欧几里得变换，包括旋转矩阵（Rotation Matrix）和平移向量（Translation Vector）。旋转矩阵表示方向变化，平移向量表示位置偏移。推导从简单到复杂，逐步构建完整转换链。

步骤1: 世界坐标系到车辆坐标系的转换

• 概念：车辆坐标系相对于世界坐标系的位置和方向变化，由车辆的位姿（位置和姿态）定义。
• 推导：
  • 设点 $P_w=\left[\begin{array}{c}{x}_w\\ y_w\\ z_w\end{array}\right]$ 在世界坐标系。
  • 设旋转矩阵 $R_{wv}$（从世界到车辆）表示方向变化，平移向量 $t_{wv}=\left[\begin{array}{c}{t}_x\\ t_y\\ t_z\end{array}\right]$ 表示车辆原点在世界坐标系中的位置。
  • 在车辆坐标系中，点 $P_v$ 的坐标为：
    $$P_v=R_{wv}(P_w-t_{wv})$$
  • 使用齐次坐标简化：
    $$\left[\begin{array}{c}{P}_v\\ 1\end{array}\right]=\left[\begin{array}{cc}{R}_{wv}& -R_{wv}{t}_{wv}\\ 0& 1\end{array}\right]\left[\begin{array}{c}{P}_w\\ 1\end{array}\right]$$
  • 定义变换矩阵 $T_{wv}=\left[\begin{array}{cc}{R}_{wv}& -R_{wv}{t}_{wv}\\ 0& 1\end{array}\right]$，则：
    $$\left[\begin{array}{c}{P}_v\\ 1\end{array}\right]=T_{wv}\left[\begin{array}{c}{P}_w\\ 1\end{array}\right]$$
  • 其中，$R_{wv}$ 是正交矩阵，满足 $R_{wv}{R}_{wv}^T=I$（单位矩阵），表示纯旋转。

步骤2: 车辆坐标系到传感器坐标系的转换

• 概念：传感器（如激光雷达）安装在车辆上，其坐标系相对于车辆坐标系有固定偏移。
• 推导：
  • 设点 $P_v=\left[\begin{array}{c}{x}_v\\ y_v\\ z_v\end{array}\right]$ 在车辆坐标系。
  • 设旋转矩阵 $R_{vs}$（从车辆到传感器）和平移向量 $t_{vs}=\left[\begin{array}{c}{t}_{sx}\\ t_{sy}\\ t_{sz}\end{array}\right]$（传感器原点在车辆坐标系中的位置）。
  • 在传感器坐标系中，点 $P_s$ 的坐标为：
    $$P_s=R_{vs}(P_v-t_{vs})$$
  • 齐次坐标形式：
    $$\left[\begin{array}{c}{P}_s\\ 1\end{array}\right]=\left[\begin{array}{cc}{R}_{vs}& -R_{vs}{t}_{vs}\\ 0& 1\end{array}\right]\left[\begin{array}{c}{P}_v\\ 1\end{array}\right]$$
  • 定义变换矩阵 $T_{vs}=\left[\begin{array}{cc}{R}_{vs}& -R_{vs}{t}_{vs}\\ 0& 1\end{array}\right]$，则：
    $$\left[\begin{array}{c}{P}_s\\ 1\end{array}\right]=T_{vs}\left[\begin{array}{c}{P}_v\\ 1\end{array}\right]$$
  • 结合步骤1，世界到传感器的转换：
    $$\left[\begin{array}{c}{P}_s\\ 1\end{array}\right]=T_{vs}{T}_{wv}\left[\begin{array}{c}{P}_w\\ 1\end{array}\right]$$

步骤3: 相机坐标系到像素坐标系的转换

• 概念：摄像头将3D点投影到2D图像平面，转换涉及相机内参（焦距、光心）。
• 推导：
  • 设点 $P_c=\left[\begin{array}{c}{x}_c\\ y_c\\ z_c\end{array}\right]$ 在相机坐标系。
  • 使用针孔相机模型：点投影到图像平面，坐标 $(x_p,y_p)$ 满足：
    $$x_p=\frac{f_x{x}_c}{z_c},y_p=\frac{f_y{y}_c}{z_c}$$
    其中 $f_x$ 和 $f_y$ 是等效焦距（考虑像素缩放）。
  • 转换到像素坐标系，考虑光心偏移 $(c_x,c_y)$：
    $$u=f_x\frac{x_c}{z_c}+c_x,v=f_y\frac{y_c}{z_c}+c_y$$
  • 写成矩阵形式：
    $$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\frac{1}{z_c}\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{x}_c\\ y_c\\ z_c\end{array}\right]$$
  • 定义相机内参矩阵 $K=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]$，则：
    $$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]\equiv K\left[\begin{array}{c}{x}_c/z_c\\ y_c/z_c\\ 1\end{array}\right]$$
    （其中 $\equiv$ 表示齐次坐标等价，需归一化处理）。

完整转换链示例：世界坐标系到像素坐标系

• 场景：给定世界坐标系中的点，如何得到其在图像中的像素位置（如用于目标检测）。
• 推导：
  • 结合所有步骤：世界坐标系 → 车辆坐标系 → 传感器坐标系（相机） → 像素坐标系。
  • 设传感器是相机，则从步骤2：$P_s=P_c$（相机坐标系）。
  • 转换链：
    $$\left[\begin{array}{c}{P}_c\\ 1\end{array}\right]=T_{vs}{T}_{wv}\left[\begin{array}{c}{P}_w\\ 1\end{array}\right]$$
    $$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\frac{1}{z_c}K\left[\begin{array}{cc}I& 0\end{array}\right]\left[\begin{array}{c}{P}_c\\ 1\end{array}\right]$$
    （其中 $\left[\begin{array}{cc}I& 0\end{array}\right]$ 提取 $P_c$ 的前三维）。
  • 完整公式：
    $$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\frac{1}{z_c}K\left[\begin{array}{cc}I& 0\end{array}\right]T_{vs}{T}_{wv}\left[\begin{array}{c}{P}_w\\ 1\end{array}\right]$$
  • 简化：令 $z_c$ 是 $P_c$ 的 $z$ 分量，计算时需先求解 $P_c$。

三、关键注意事项

• 旋转矩阵计算：旋转矩阵通常由欧拉角或四元数推导。例如，绕 $z$ 轴旋转 $\theta$ 角：
  $$R_z(\theta )=\left[\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]$$
• 误差处理：实际系统中，转换参数（如 $R_{wv}$, $t_{wv}$）通过标定获得，可能涉及优化算法（如最小二乘法）减少误差。
• 应用：这些转换用于传感器融合（如融合摄像头和激光雷达数据）、路径规划等。确保转换链一致，避免累积误差。

这个推导基于标准几何原理，在自动驾驶系统中广泛应用。如果您有具体场景（如特定传感器类型），我可以进一步细化推导。