E1. Submedians (Easy Version)

题目：

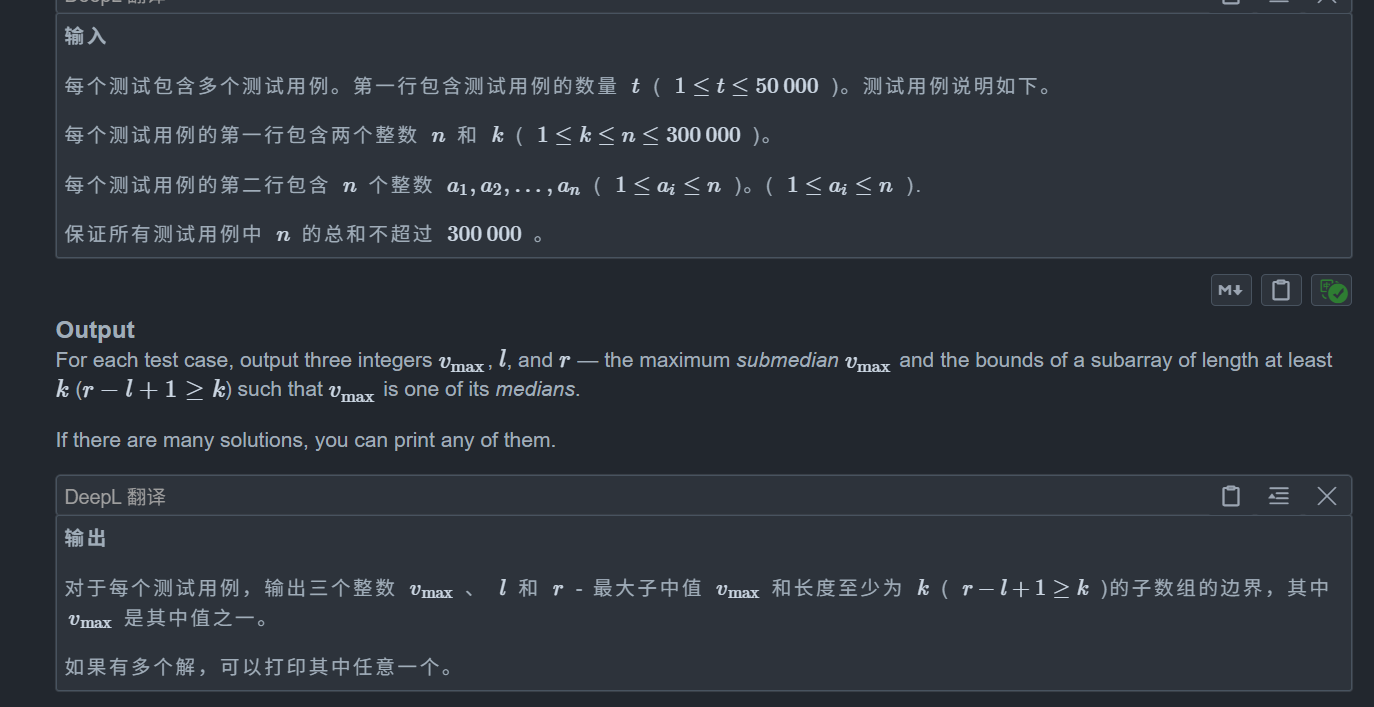思路：

经典不过加了点东西

对于求中位数，我们必然要想到二分答案，具体的，对于所有大于等于 x 的数我们令其奉献为 1，小于的为 -1，如果存在某段区间的奉献和大于等于 0，那么就说明这段区间的中位数大于等于 x

本题也一样，由于题目要求长度要大于等于 k，因此我们要存储最小的左端点，且距离 i 大于等于 k，具体看代码

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "Yes\n"
#define no cout << "No\n"
int n, k;
int a[300005];
int sum[300005];
void solve()
{cin >> n >> k;for (int i = 1; i <= n; i++){cin >> a[i];}int l = 0, r = 300000;auto check = [&](int x) -> tuple<int, int, int>{for (int i = 1; i <= n; i++){sum[i] = sum[i - 1] + (a[i] >= x ? 1 : -1);}int mi = 0,mipos = 0;for (int i = k; i <= n; i++){if (sum[i] - mi >= 0){return {1, mipos+1, i};}int j = i - k  +1;if(sum[j] < mi){mi = sum[j];mipos = j;}}return {0, 0, 0};};while (l + 1 < r){int mid = l + r >> 1;auto [flag, a, b] = check(mid);if (flag){l = mid;}else{r = mid;}}auto [f, L, R] = check(r);if (f){cout << r << " " << L << " " << R << endl;return;}auto [ f2, a, b ] = check(l);cout << l << " " << a << " " << b << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}