1、希尔排序介绍

1.1、定义

1.2、核心思想

2、希尔排序的流程

第 1 轮：gap = 4

第 2 轮：gap = 2

第 3 轮：gap = 1

3、希尔排序的实现

4、时间复杂度分析

5、希尔排序的优缺点

6、适用场景

前言

希尔排序（Shell Sort）是一种基于插入排序的高效排序算法，由 Donald Shell 在 1959 年提出。

gap（间隔）是希尔排序的核心，它决定了如何将数组分成若干子序列进行插入排序。

初始 gap 较大（如 n/2），逐步缩小，直到 gap = 1（此时就是普通插入排序）。
每次按 gap 分组后，对每组进行独立的插入排序。

gap的作用：

gap 的作用：
- 控制分组的间隔，让元素能“长距离跳跃”，减少后续操作次数。
子序列的划分：
- 每隔 gap 个元素取一个值，形成一组，组内进行插入排序。
为什么快？
- 大步长让数据快速接近有序，小步长最终精细化调整。

1、希尔排序介绍

1.1、定义

它通过引入分组间隔（gap）来优化插入排序的性能，使得元素能够更快地移动到正确的位置，从而减少比较和交换的次数。

1.2、核心思想

1、分组插入排序：

将整个数组按照一定的间隔（gap）分成若干子序列，对每个子序列进行插入排序。

2、逐步缩小间隔：

随着排序的进行，gap 不断缩小，直到 gap = 1（此时相当于普通的插入排序）。

3、最终排序：

当 gap = 1 时，数组已经基本有序，插入排序的效率会非常高（接近 O(n)）。

为什么比普通插入排序快？

插入排序在数据基本有序时效率很高（接近 O(n)），但在完全逆序时效率很低（O(n²)）。

希尔排序通过先让数据“大致有序”，再执行插入排序，从而显著提高性能。

2、希尔排序的流程

如下图所示：

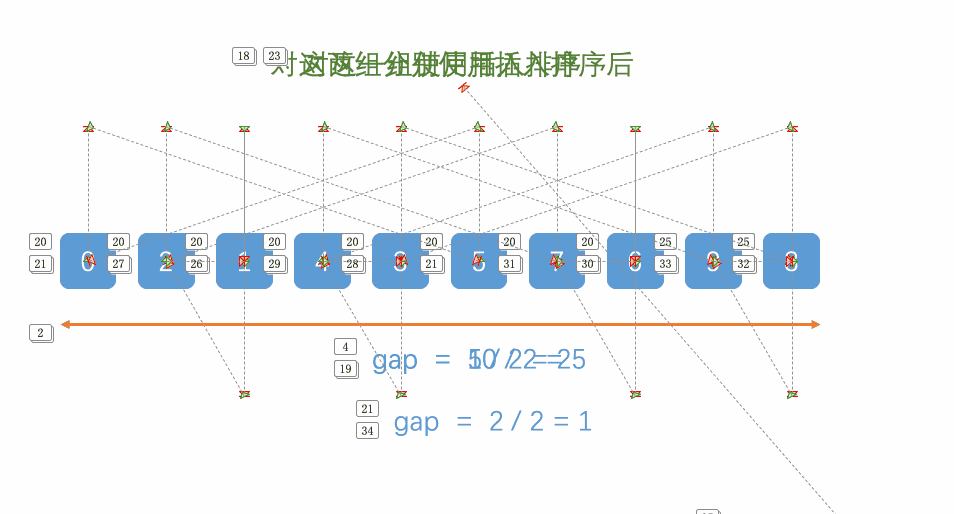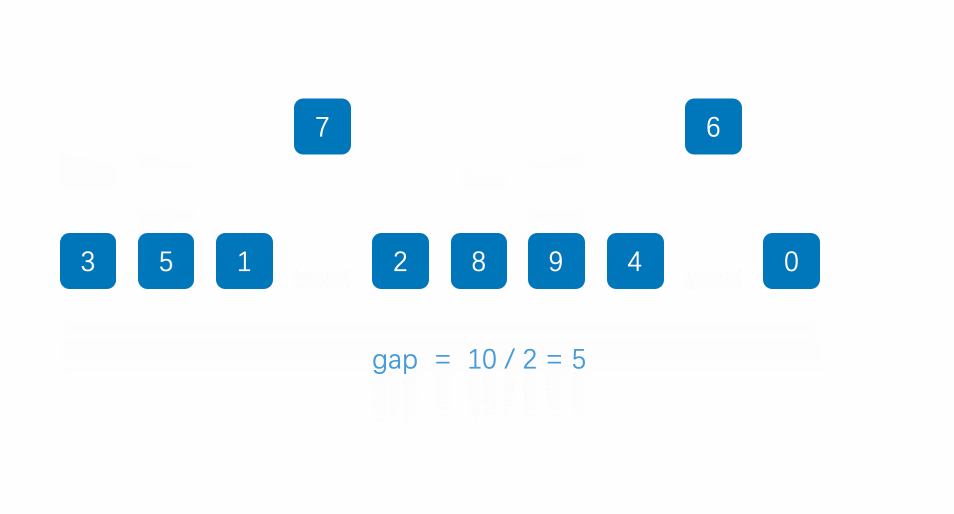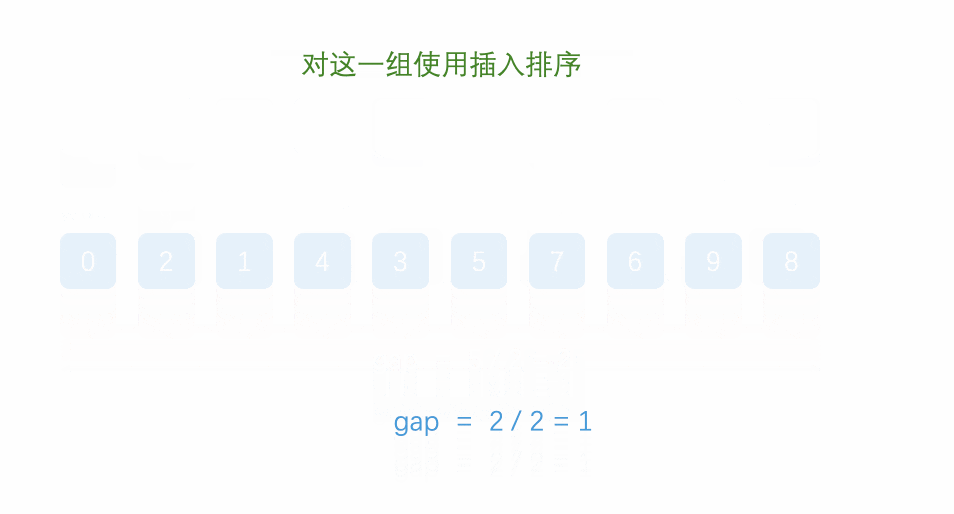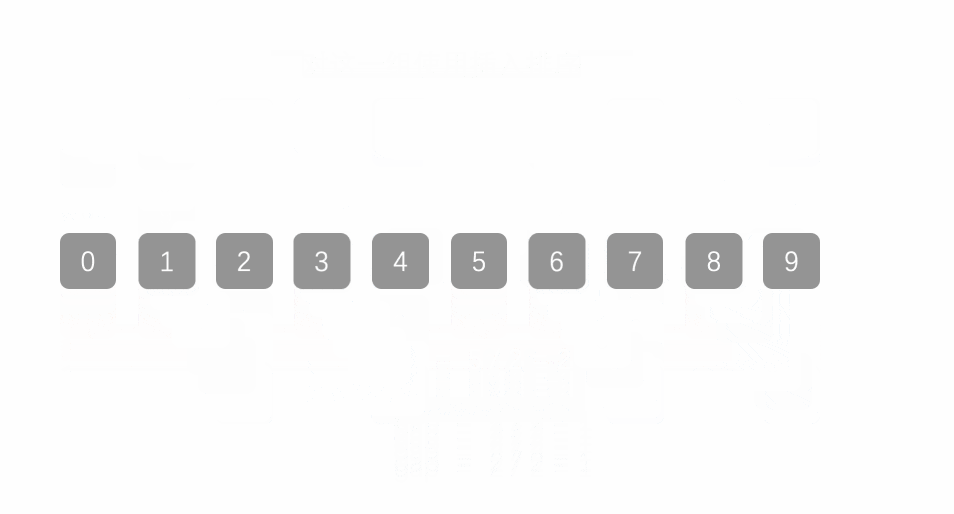
示例：

选择一个 gap 序列（如 n/2, n/4, ..., 1）。
对每个 gap 值，将数组分成若干子序列，并对每个子序列进行插入排序。
逐步缩小 gap，重复上述过程，直到 gap = 1 完成最终排序。

示例（gap = 4, 2, 1）：

原始数组：[8, 3, 6, 2, 1, 9, 5, 7, 4]

假设数组为 [8, 3, 6, 2, 1, 9, 5, 7, 4]，长度为 n = 9。
我们以 Shell 原始序列（gap = n/2, n/4, ..., 1）为例：

第 1 轮：gap = 4

将数组按间隔 4 分组，即每隔 4 个元素取一个元素，形成子序列：
- 子序列 1：arr[0], arr[4], arr[8] → [8, 1, 4]
- 子序列 2：arr[1], arr[5] → [3, 9]（因为 arr[9] 越界，停止）
- 子序列 3：arr[2], arr[6] → [6, 5]
- 子序列 4：arr[3], arr[7] → [2, 7]
对每个子序列进行插入排序：
- [8, 1, 4] → [1, 4, 8]
- [3, 9] → [3, 9]（已有序）
- [6, 5] → [5, 6]
- [2, 7] → [2, 7]（已有序）
排序后数组：
将子序列按原位置写回数组：
- arr[0]=1, arr[4]=4, arr[8]=8 → [1, 3, 5, 2, 4, 9, 6, 7, 8]

第 2 轮：gap = 2

按间隔 2 分组：
- 子序列 1：arr[0], arr[2], arr[4], arr[6], arr[8] → [1, 5, 4, 6, 8]
- 子序列 2：arr[1], arr[3], arr[5], arr[7] → [3, 2, 9, 7]
插入排序：
- [1, 5, 4, 6, 8] → [1, 4, 5, 6, 8]（交换 5 和 4）
- [3, 2, 9, 7] → [2, 3, 7, 9]（交换 3 和 2，然后 9 和 7）
排序后数组：[1, 2, 4, 3, 5, 7, 6, 9, 8]

第 3 轮：gap = 1

此时就是普通插入排序，但数组已基本有序：
- 从 i=1 开始，逐个将元素插入到左侧已排序部分。
- 最终结果：[1, 2, 3, 4, 5, 6, 7, 8, 9]

3、希尔排序的实现

代码示例如下：

import java.util.Arrays;public class ShellSort {/*** 希尔排序（Shell Sort）* @param arr 待排序数组*/public static void shellSort(int[] arr) {if (arr == null || arr.length <= 1) {return; // 如果数组为空或长度≤1，无需排序}int n = arr.length;// 1. 初始化间隔（gap），这里使用 Shell 原始序列：n/2, n/4, ..., 1for (int gap = n / 2; gap > 0; gap /= 2) {// 2. 对每个子序列进行插入排序（从 gap 开始，逐步向右扫描）for (int i = gap; i < n; i++) {int temp = arr[i]; // 当前待插入元素int j;// 3. 插入排序逻辑：比 temp 大的元素向后移动for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {arr[j] = arr[j - gap]; // 较大的元素后移}// 4. 将 temp 插入到正确位置arr[j] = temp;}// （可选）打印每轮排序后的数组，方便理解过程System.out.println("Gap = " + gap + ": " + Arrays.toString(arr));}}public static void main(String[] args) {int[] arr = {8, 3, 6, 2, 1, 9, 5, 7, 4};System.out.println("原始数组: " + Arrays.toString(arr));shellSort(arr);System.out.println("排序后数组: " + Arrays.toString(arr));}
}

关键步骤说明

初始化间隔（gap）：
- 初始 gap = n / 2（Shell 原始序列），之后每次缩小为 gap / 2，直到 gap = 1。
- 例如，数组长度 n = 9，则 gap 序列为 4 → 2 → 1。
子序列插入排序：
- 从 i = gap 开始，逐步向右扫描，对每个子序列进行插入排序。
- 示例（gap = 4）：
  - 子序列 1：arr[0], arr[4], arr[8]（即 8, 1, 4 → 排序后 1, 4, 8）
  - 子序列 2：arr[1], arr[5]（即 3, 9 → 排序后 3, 9）
  - 子序列 3：arr[2], arr[6]（即 6, 5 → 排序后 5, 6）
  - 子序列 4：arr[3], arr[7]（即 2, 7 → 排序后 2, 7）
插入排序逻辑：
- 类似普通插入排序，但步长是 gap 而不是 1。
- 如果 arr[j - gap] > temp，则向后移动元素。
插入最终位置：
- 将 temp 放到正确的位置 arr[j]。

输出：

原始数组: [8, 3, 6, 2, 1, 9, 5, 7, 4]
Gap = 4: [1, 3, 5, 2, 4, 9, 6, 7, 8]
Gap = 2: [1, 2, 4, 3, 5, 7, 6, 9, 8]
Gap = 1: [1, 2, 3, 4, 5, 6, 7, 8, 9]
排序后数组: [1, 2, 3, 4, 5, 6, 7, 8, 9]

4、时间复杂度分析

如下所示：

常见 gap 序列的影响：

Shell 原始序列（n/2, n/4, ..., 1）：最坏 O(n²)。
Hibbard 序列（1, 3, 7, 15, ..., 2^k -1）：最坏 O(n^(3/2))。
Knuth 序列（1, 4, 13, 40, ..., (3^k -1)/2）：平均 O(n^(3/2))。

Java 的 Arrays.sort() 在特定情况下会使用希尔排序的变种（如 TimSort 结合插入排序优化）。

5、希尔排序的优缺点

1、优点

比普通插入排序快，尤其是对中等规模数据（n ≤ 10⁴）。
原地排序，空间复杂度 O(1)。
适用于部分有序数据，性能接近 O(n)。

2、缺点

不稳定排序（可能改变相同元素的相对顺序）。
时间复杂度依赖 gap 序列，选择不当可能退化到 O(n²)。

6、适用场景

中小规模数据排序（比插入排序更快，比快速排序/归并排序更节省内存）。
嵌入式系统或内存受限环境（因为它是原地排序）。
部分有序数据（性能接近线性时间）。

总结

希尔排序是插入排序的优化版本，通过分组排序减少元素移动次数。
时间复杂度介于 O(n log n) ~ O(n²)，取决于 gap 序列的选择。
适用于中小规模数据，在特定情况下比快速排序/归并排序更高效。

如果你需要对中等规模数据进行排序，并且希望节省内存，希尔排序是一个不错的选择！

参考文章：

1、六大排序算法：插入排序、希尔排序、选择排序、冒泡排序、堆排序、快速排序-CSDN博客https://blog.csdn.net/weixin_50886514/article/details/119045154?ops_request_misc=%257B%2522request%255Fid%2522%253A%25220faf03d22b2d125d5f49a4649ad59c85%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=0faf03d22b2d125d5f49a4649ad59c85&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-119045154-null-null.142^v102^control&utm_term=%E5%86%92%E6%B3%A1%E6%8E%92%E5%BA%8F&spm=1018.2226.3001.4187