目录
一. 树的概念和结构
1.1 树的基本概念
1.2 树的结构特点
二. 树的表示方法和实际运用
2.1 孩子 - 兄弟表示法(Child-Sibling Representation)
2.2 树的实际应用场景
三. 二叉树的概念
3.1 二叉树的核心定义
3.2 二叉树的基本分类
四. 二叉树的性质
性质 1:节点数量与层数的关系
性质 2:深度与总节点数的关系
性质 3:叶子节点与度为 2 的节点的关系
性质 4:完全二叉树的深度
性质 5:完全二叉树的节点索引关系
五. 二叉树的存储结构
一、顺序存储结构
二、链式存储结构
一. 树的概念和结构
在数据结构中,树(Tree) 是一种非线性的数据结构,它由节点(Node)和边(Edge)组成,用于表示具有层次关系的数据。树的结构类似于自然界中的树,具有 “根”、“枝”、“叶” 等概念,但其形态是 “倒置” 的(根在上,叶在下)。
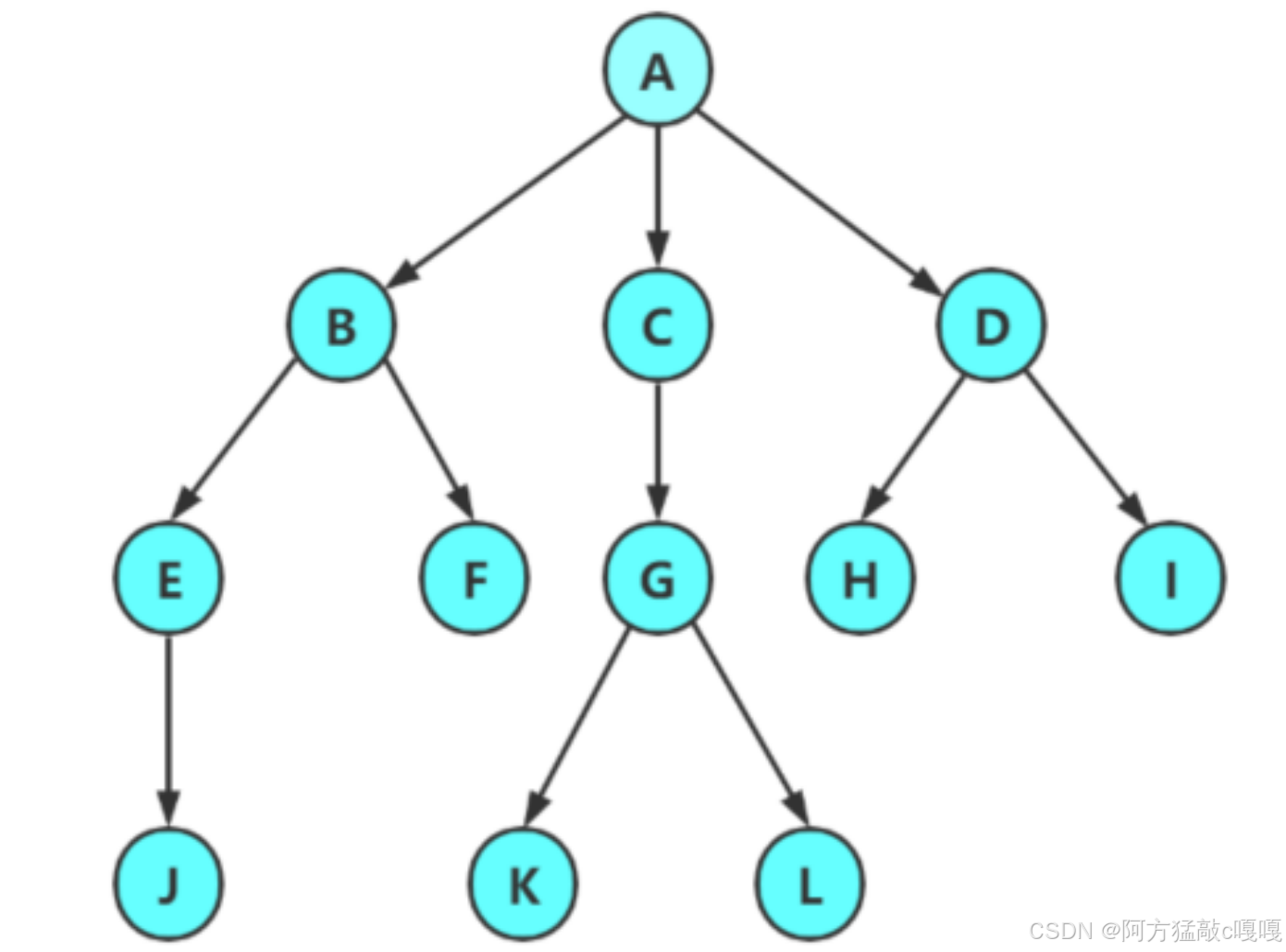
由上图可以推测出 每一个节点只有向上和向下链接 如果出现了左右链接 则不是树结构 如下:

1.1 树的基本概念
节点(Node)
树的基本组成单位,包含数据和指向子节点的引用(指针)。根节点(Root)
树的起点,没有父节点的节点(一棵树有且仅有一个根节点)。父节点与子节点
若节点 A 直接指向节点 B,则 A 是 B 的父节点,B 是 A 的子节点。
同一父节点的子节点互称为兄弟节点。
叶子节点(Leaf)
没有子节点的节点(即度为 0 的节点)。度(Degree)
一个节点拥有的子节点数量(叶子节点的度为 0,根节点的度至少为 1)。深度(Depth)
从根节点到当前节点的路径长度(根节点深度为 0 或 1,通常以 0 开始)。高度(Height)
从当前节点到最深叶子节点的路径长度(叶子节点高度为 0,根节点高度即树的高度)。路径(Path)
从一个节点到另一个节点经过的节点序列(树中路径唯一,无环)。子树(Subtree)
以某节点为根的所有后代节点组成的树(该节点及其子树是原树的一部分)。
1.2 树的结构特点
- 非线性结构:节点之间的关系不是线性的,而是层次化的。
- 无环性:任意两个节点之间有且仅有一条路径,不存在回路(环)。
- 根的唯一性:只有一个根节点,所有其他节点都直接或间接依附于根。
- 子树独立性:一棵树的子树之间互不相交(否则会形成环)。
二. 树的表示方法和实际运用
树的表示方法有很多 现在我向大家介绍孩子兄弟表示法
2.1 孩子 - 兄弟表示法(Child-Sibling Representation)
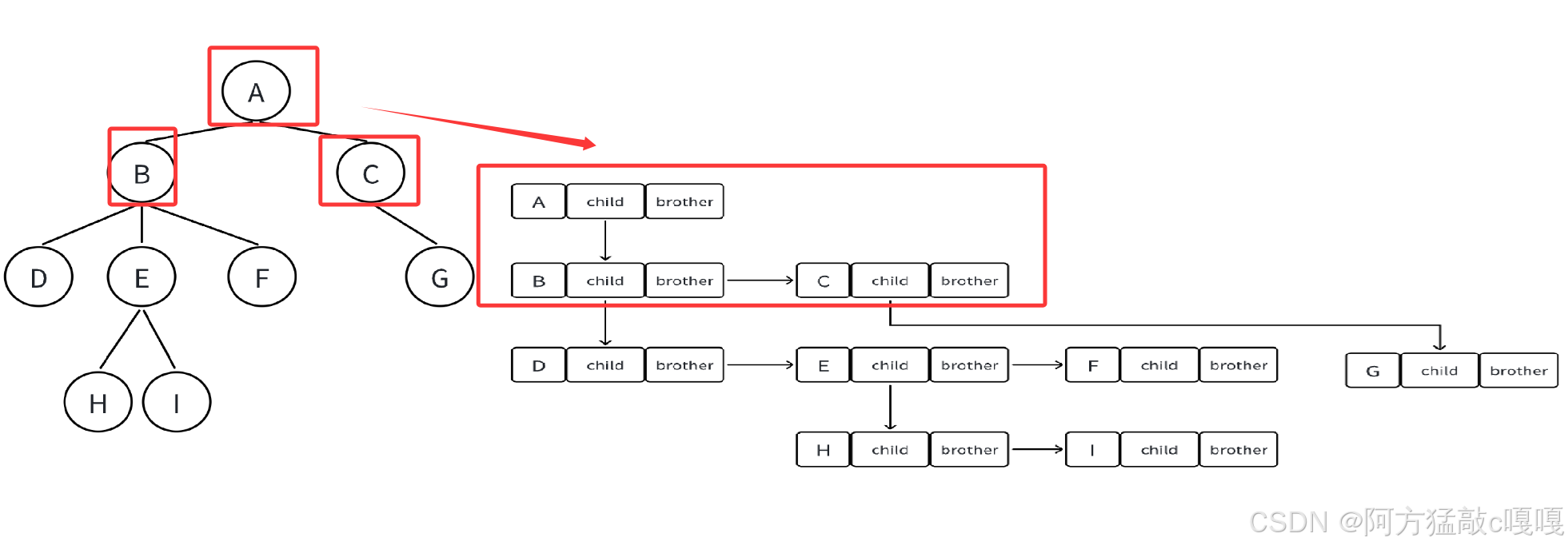
- 原理:将任意树转换为二叉树结构,每个节点包含三个部分:
- 数据域;
- 第一个子节点指针(指向最左子节点);
- 右兄弟节点指针(指向同一父节点的下一个兄弟节点)。
- 结构示例(将多叉树转为二叉树):
(原树中 A 的子节点是 B、C、D;B 的子节点是 E、F)A/B → C → D (B的右兄弟是C,C的右兄弟是D)/E → F (E的右兄弟是F) - 优点:将多叉树统一为二叉树结构,可复用二叉树的算法(如遍历、插入),节省空间。
- 缺点:结构较抽象,需理解 “兄弟节点” 的转换逻辑。
- 适用场景:多叉树与二叉树的转换(如森林的表示、语法树的存储)。
struct TreeNode
{struct Node* child; // 左边开始的第⼀个孩⼦结点struct Node* brother; // 指向其右边的下⼀个兄弟结点int data; // 结点中的数据域
};
2.2 树的实际应用场景
树的层次化、无环特性使其在解决具有 “父子关系”“层级分类” 的问题时极为高效,以下是典型场景:
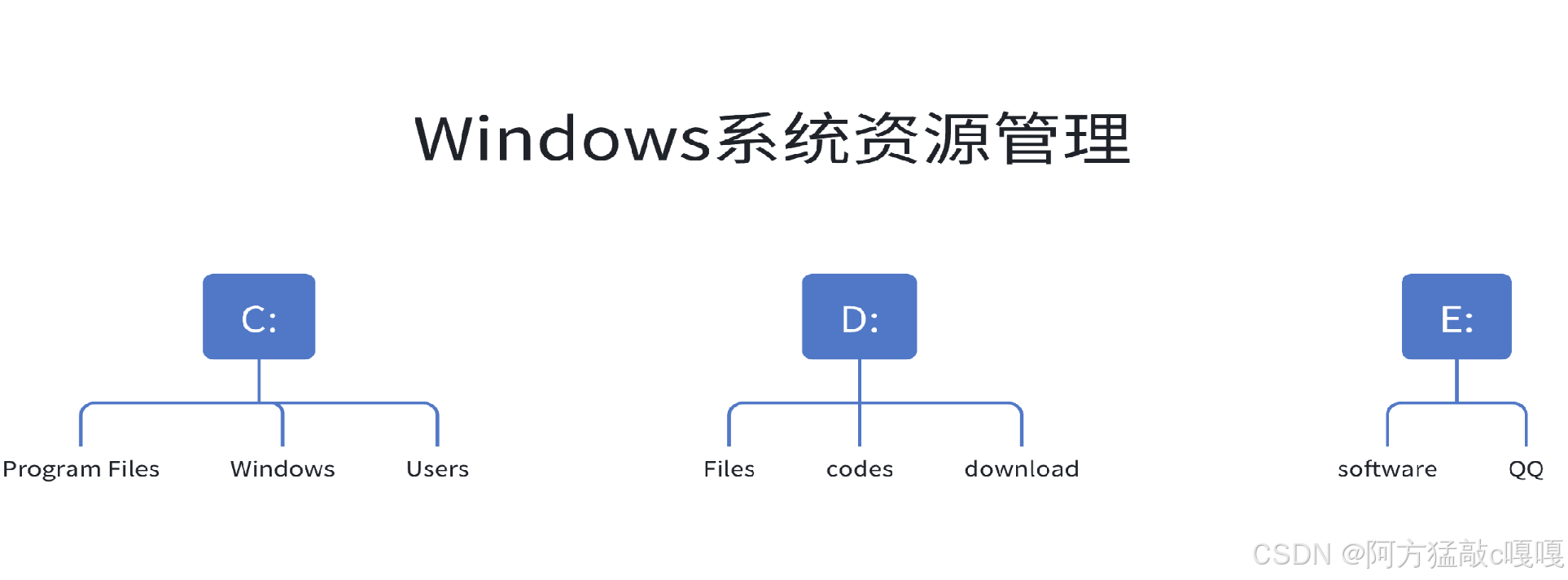
1. 文件系统与目录结构
- 原理:操作系统的文件和文件夹以树状组织,根目录为根节点,文件夹为中间节点,文件为叶子节点。
- 示例:Windows 的
C:\Users\Document\file.txt是一条从根到叶子的路径。- 优势:支持高效的路径查找(如
cd命令遍历目录)和层级管理。2. 数据库索引
- 原理:B 树、B + 树等多叉树结构被用于数据库索引,平衡的树高保证了查询、插入、删除的高效性(时间复杂度 O (log n))。
- 示例:MySQL 的 InnoDB 存储引擎使用 B + 树作为聚簇索引,叶子节点存储完整数据行,非叶子节点作为索引指引。
三. 二叉树的概念
下面向大家介绍树中最常见也是最常用的结构---二叉树
二叉树(Binary Tree)是一种特殊的树结构,每个节点最多有两个子节点,分别称为左子节点和右子节点。这种 “最多两个子节点” 的特性使其结构相对简单,同时具备树的层次化、非线性特点,是数据结构中最常用的树类型之一。
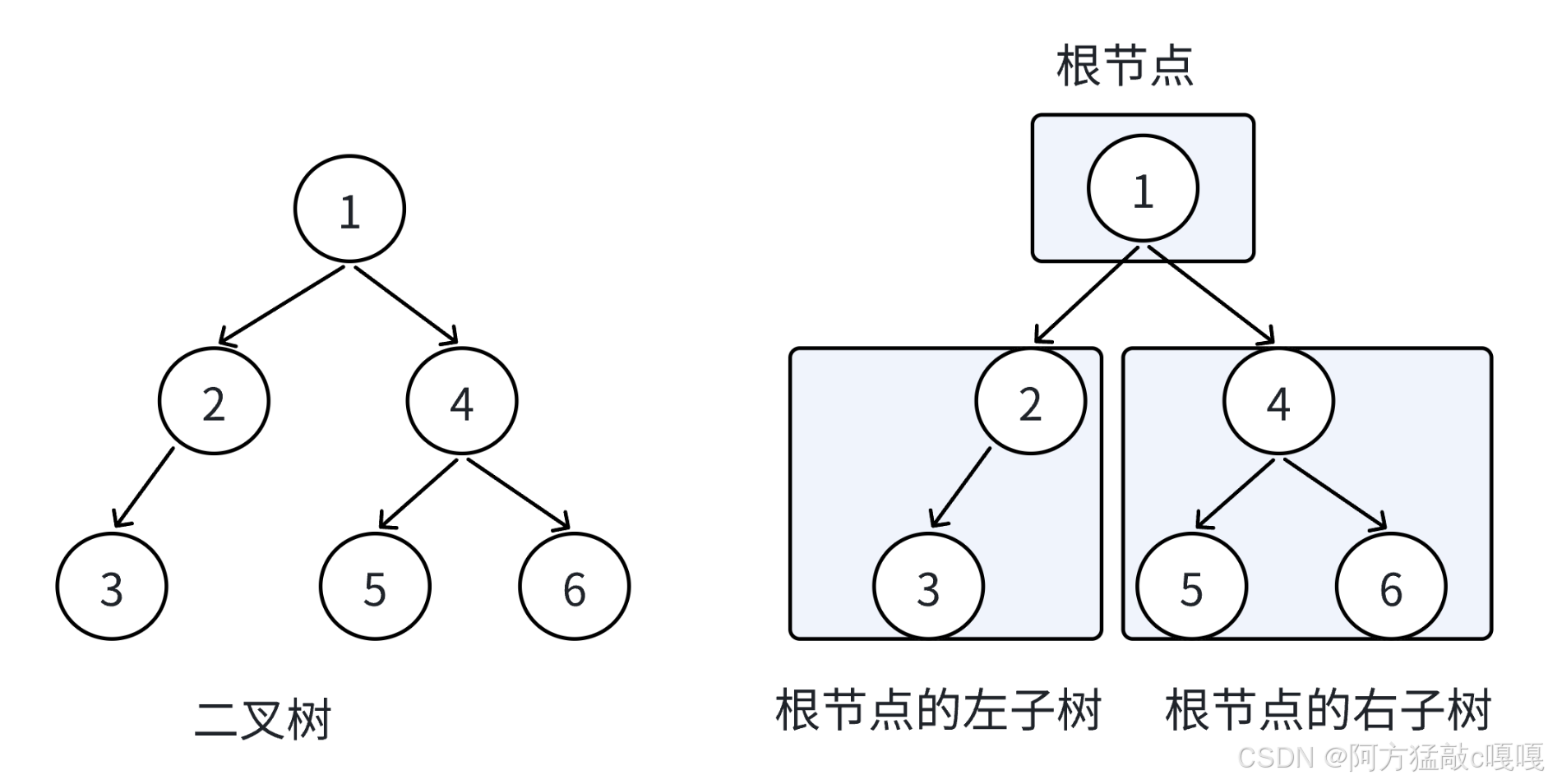
从上图可以看出 二叉树即最多二分叉 所以最多只有两个子节点 下面看一下二叉树的核心定义
3.1 二叉树的核心定义
-
节点结构:每个节点包含三部分:
- 数据域(存储节点值);
- 左子节点指针(指向左侧子节点,无则为
null); - 右子节点指针(指向右侧子节点,无则为
null)。
-
基本特性:
- 根节点:无父节点的节点(二叉树有且仅有一个根节点,除非是空树)。
- 叶子节点:左、右子节点均为
null的节点(无子女)。 - 子树:以某个节点的左 / 右子节点为根的树,称为该节点的左 / 右子树(子树本身也是二叉树)。
- 层次(深度):根节点为第 1 层,其子节点为第 2 层,以此类推。
- 高度:节点到最深叶子节点的路径长度(叶子节点高度为 1)。
3.2 二叉树的基本分类
-
空二叉树:没有任何节点的树。
-
满二叉树(Full Binary Tree):
- 所有非叶子节点都有两个子节点;
- 所有叶子节点在同一层次(即最后一层)。
例如 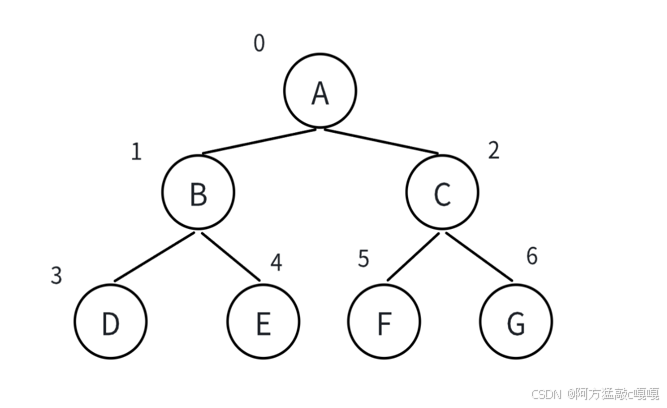
-
完全二叉树(Complete Binary Tree):
- 除最后一层外,所有层的节点数都达到最大值;
- 最后一层的节点从左到右连续排列(不允许右侧有空缺);
- 满二叉树是完全二叉树的特例。
例如(最后一层节点从左到右连续):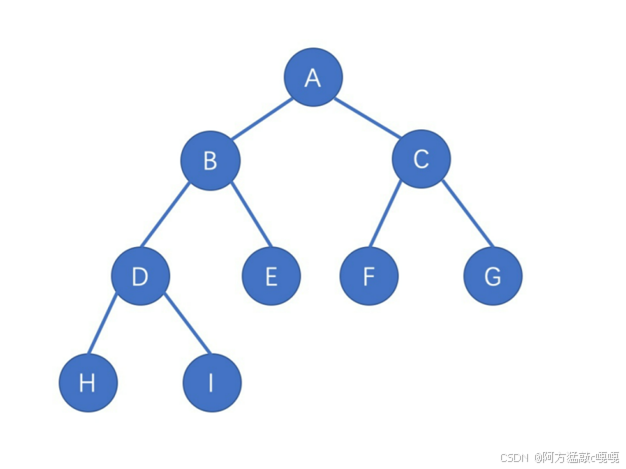
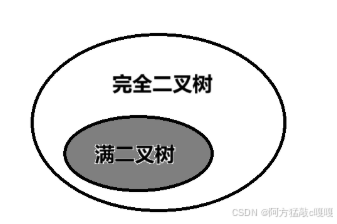
满二叉树属于一种特殊的完全二叉树 关系图如下
四. 二叉树的性质
性质 1:节点数量与层数的关系
第 i 层最多有 2^(i-1) 个节点(i ≥ 1,层数从 1 开始计数)。
推导:第 1 层(根节点)最多 1 个节点(
2^0);第 2 层最多 2 个节点(2^1);第 3 层最多 4 个节点(2^2)…… 第i层最多为2^(i-1)个节点(每一层节点数是上一层的 2 倍,因每个节点最多 2 个子节点)。
性质 2:深度与总节点数的关系
深度为 k 的二叉树,最多有 2^k - 1 个节点(k ≥ 1)。
推导:总节点数为各层最大节点数之和,即
2^0 + 2^1 + 2^2 + ... + 2^(k-1) = 2^k - 1(等比数列求和)。特例:满二叉树的总节点数恰好为
2^k - 1(每一层都达到最大节点数)。
性质 3:叶子节点与度为 2 的节点的关系
对任何一棵二叉树,若叶子节点数为 n₀,度为 2 的节点数为 n₂,则 n₀ = n₂ + 1。
-
推导:
-
设度为 1 的节点数为
n₁,总节点数N = n₀ + n₁ + n₂。 -
二叉树中,除根节点外,每个节点都有且仅有一个父节点,因此总边数为
N - 1(边数 = 节点数 - 1)。 -
边数也可由节点的度计算:度为 1 的节点贡献 1 条边,度为 2 的节点贡献 2 条边,叶子节点(度为 0)贡献 0 条边,因此总边数
= n₁×1 + n₂×2。 -
联立得:
n₀ + n₁ + n₂ - 1 = n₁ + 2n₂,化简后n₀ = n₂ + 1。
-
性质 4:完全二叉树的深度
具有 n 个节点的完全二叉树,其深度为 ⌊log₂n⌋ + 1(⌊x⌋ 表示向下取整)。
-
推导:
-
设深度为
k,则完全二叉树的节点数n满足:
深度为k-1的满二叉树节点数 <n≤ 深度为k的满二叉树节点数,
即2^(k-1) - 1 < n ≤ 2^k - 1。 -
不等式变形为
2^(k-1) ≤ n < 2^k,两边取对数得k-1 ≤ log₂n < k,因此k = ⌊log₂n⌋ + 1。
-
性质 5:完全二叉树的节点索引关系
对有
n个节点的完全二叉树,若按层次(从左到右)给节点编号(从 1 开始),则对任意节点i(1 ≤ i ≤ n):
若
i > 1,则其父节点编号为⌊i/2⌋(左子节点的父节点为i/2,右子节点的父节点为(i-1)/2,统一为⌊i/2⌋)。若
2i ≤ n,则其左子节点编号为2i;否则无左子节点(叶子节点)。若
2i + 1 ≤ n,则其右子节点编号为2i + 1;否则无右子节点。例:编号为 3 的节点,父节点为
⌊3/2⌋ = 1,左子节点为6(若存在),右子节点为7(若存在)。
这些性质是二叉树遍历、构建(如堆的实现)、操作(如查找父 / 子节点)的理论基础,尤其在完全二叉树和满二叉树中应用广泛。
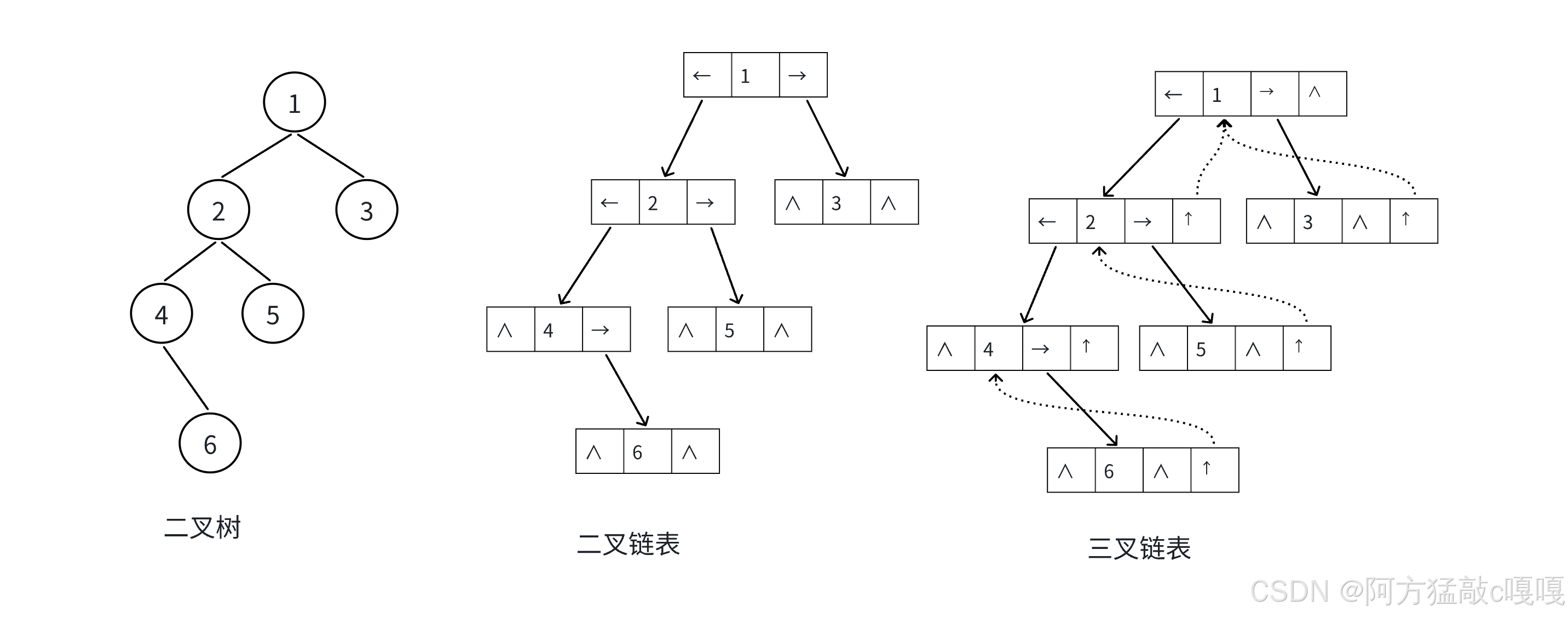
五. 二叉树的存储结构
二叉树的存储结构需要兼顾其逻辑特性(节点间的父子关系)和操作效率(如访问子节点、父节点),常见的存储方式有两种:顺序存储结构和链式存储结构。
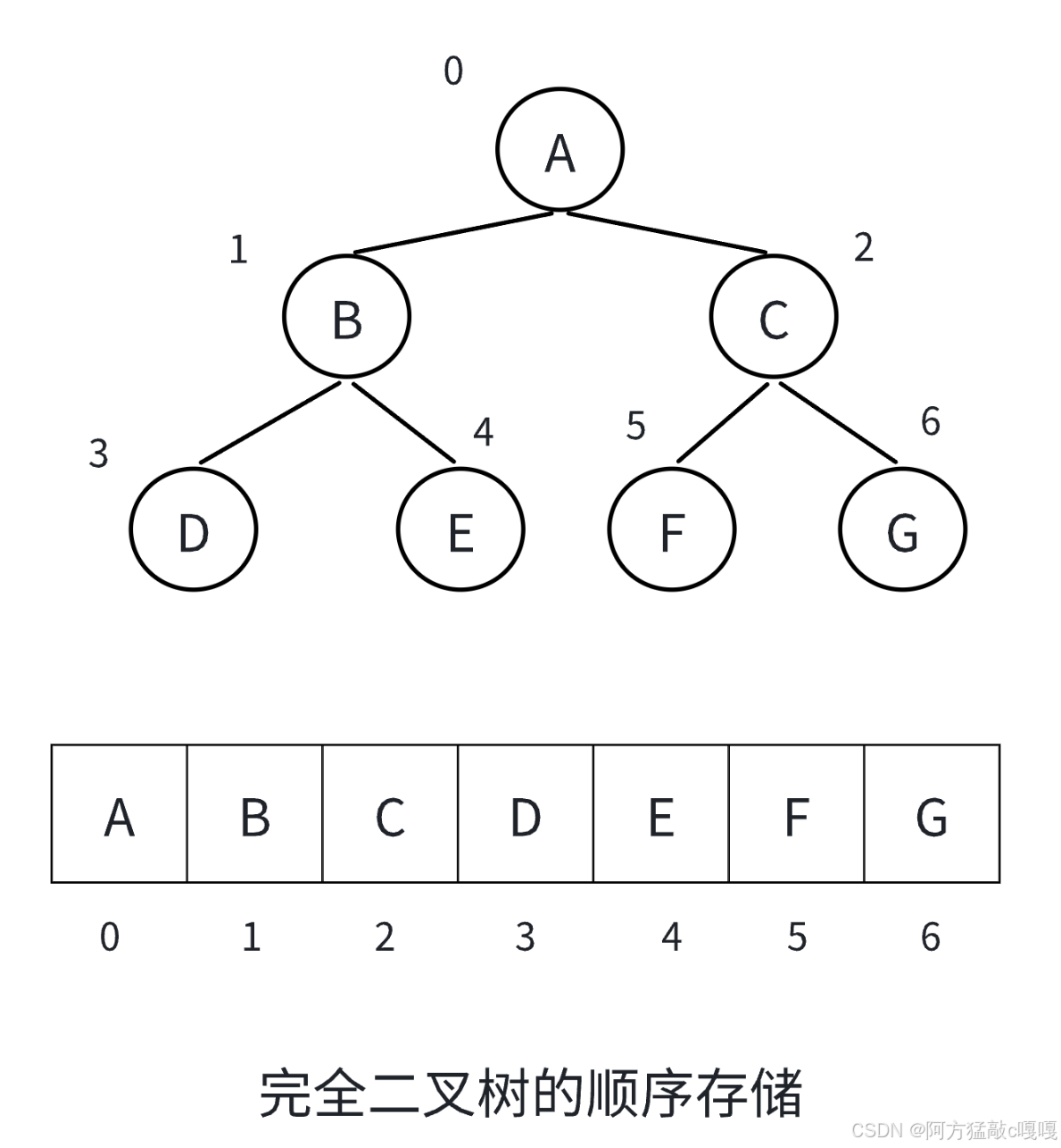
一、顺序存储结构
顺序存储通过数组存储二叉树的节点,利用节点在数组中的索引位置反映其逻辑关系(父子、左右兄弟)。
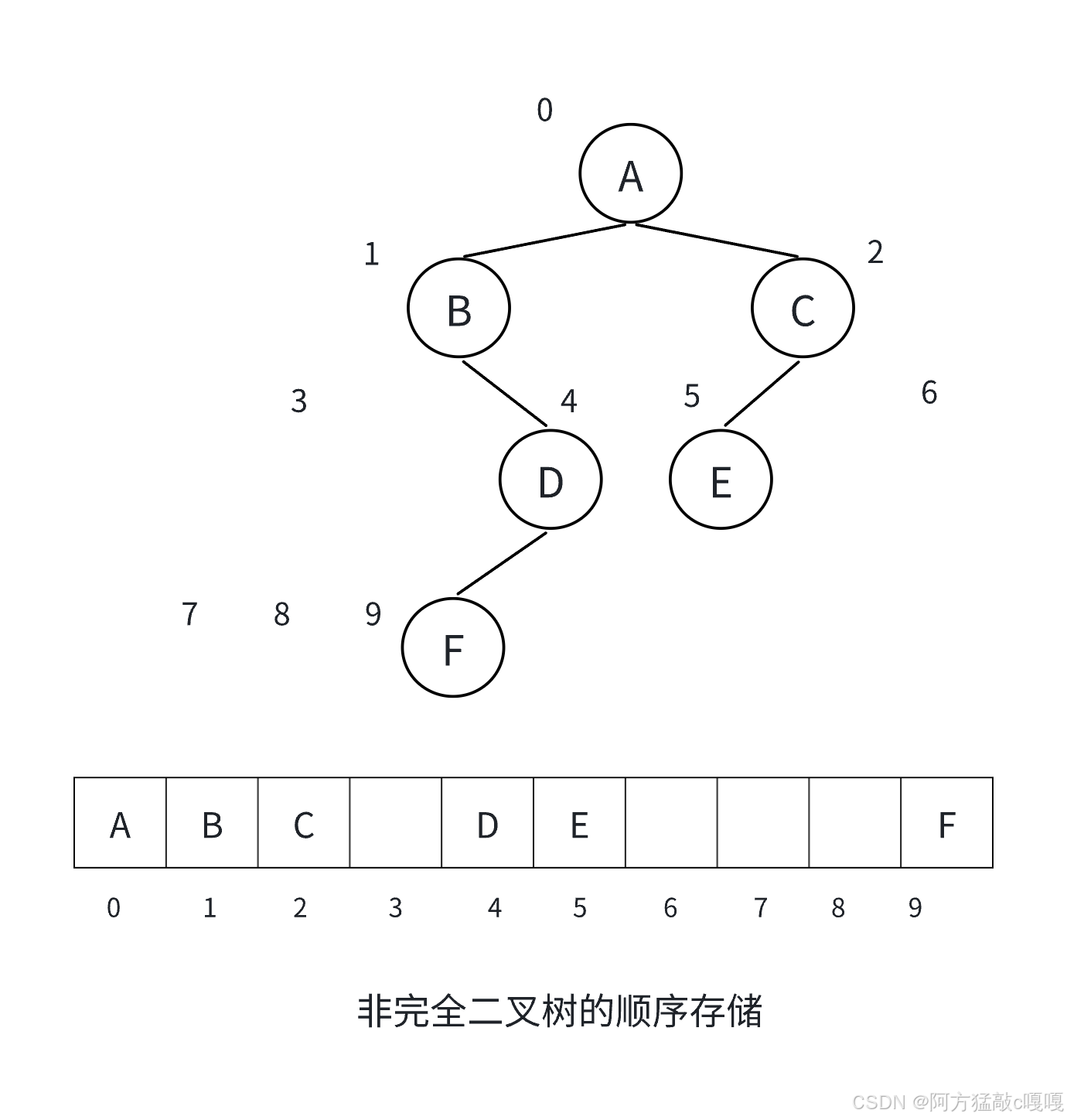
适用场景:完全二叉树(或满二叉树),此时数组空间利用率最高;非完全二叉树会浪费较多空间。
存储规则
按层次遍历顺序(从根到叶,每层从左到右)将节点存入数组,索引从 0 或 1 开始(通常从 1 开始,便于计算父子关系)。
假设数组索引从 1 开始,对于任意节点 i:
- 左子节点索引:
2i(若存在); - 右子节点索引:
2i + 1(若存在); - 父节点索引:
i // 2(i > 1时)。
示例
完全二叉树的顺序存储:
优缺点
- 优点:访问子节点 / 父节点效率高(通过公式直接计算索引,时间复杂度
O(1));适合完全二叉树(无空间浪费)。 - 缺点:非完全二叉树需用
null填充空缺位置,空间利用率低;插入 / 删除节点时可能需要大量移动元素,效率低。
二、链式存储结构
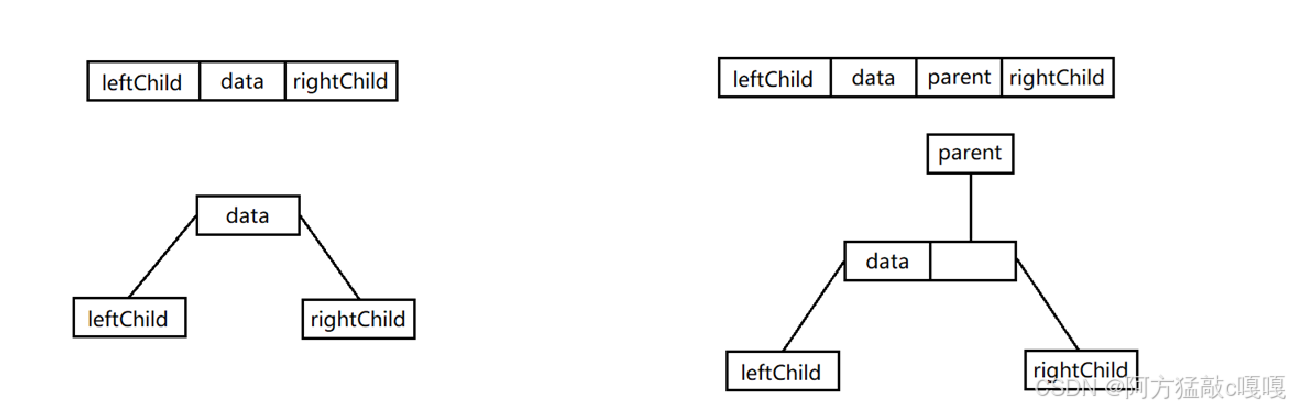
链式存储通过指针(或引用) 连接节点,每个节点存储自身数据及指向子节点的指针,更灵活地表示任意二叉树。
节点结构
每个节点包含 3 个域:
- 数据域:存储节点的值;
- 左指针域:指向左子节点(
left); - 右指针域:指向右子节点(
right)。
// C语言示例
typedef struct BiTNode {int data; // 数据域struct BiTNode *left; // 左子节点指针struct BiTNode *right; // 右子节点指针
} BiTNode, *BiTree;
任意二叉树的链式存储:



——微调Transformer语言模型进行回归分析)

——系统包管理)







)




)
