鱼眼相机模型
最近涉及鱼眼相机模型、标定使用等,作为记录,更新很久不曾更新的博客。
文章目录
- 鱼眼相机模型
- 1 相机成像
- 2 鱼眼模型
- 3 畸变
- 3.1 适用针孔和MEI
- 3.2 Kannala-Brandt鱼眼模型
- 4 代码实现
1 相机成像
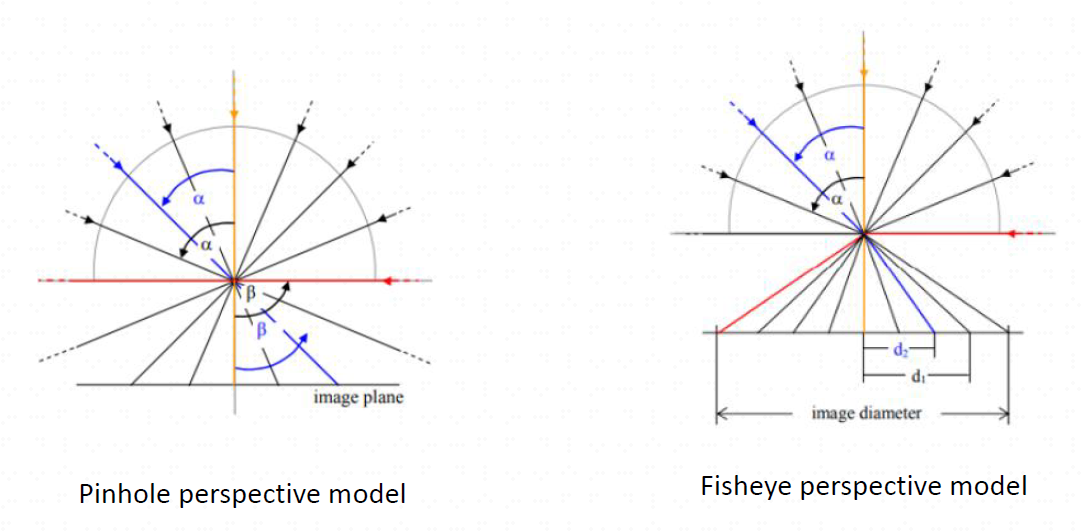
针孔相机:所有光线从一个孔(光心)透过,入射角θ\thetaθ = 出射角θd\theta_{d}θd。0-180°的光线汇聚的图像是无穷大的,所以针孔相机的视场角一般都很小。
鱼眼相机:类似于凸透镜成像,光线被聚集,入射角θ\thetaθ > 出射角θd\theta_{d}θd。光线汇聚的图像变小,所以鱼眼相机的视场角一般可以达到18-270°。
2 鱼眼模型
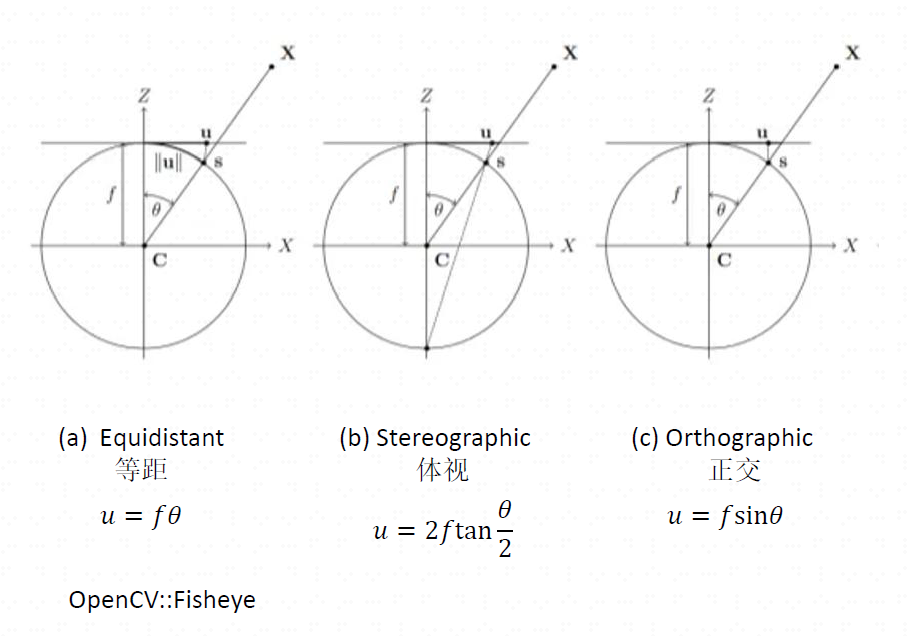
常见模型,注意,这里的θ\thetaθ是入射角!!θd\theta_{d}θd才是出射角。
VINS、AVP-SLAM中采用的MEI模型--------
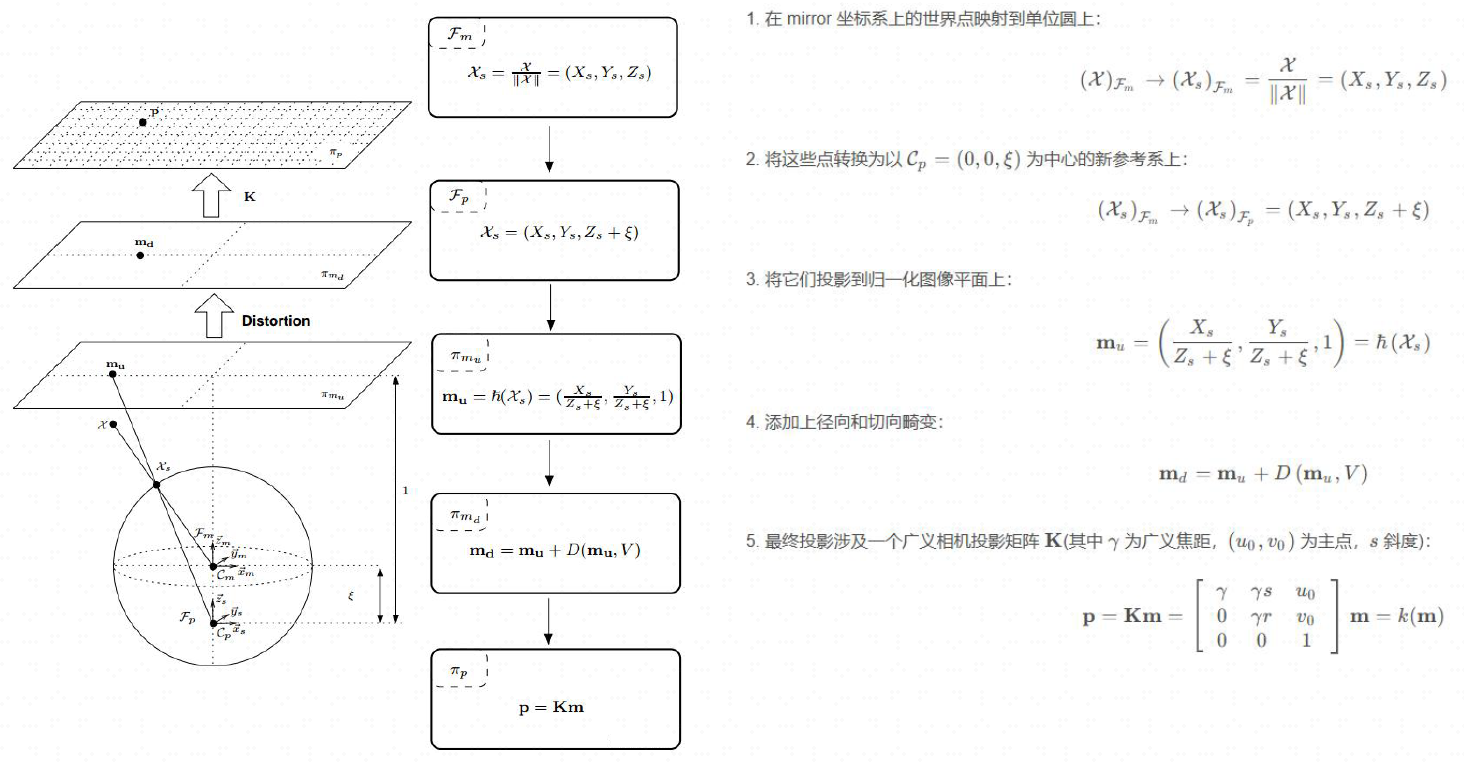
注意,常规鱼眼模型的去畸变和针孔相机不同,可以见
opencv中解释;但是MEI模型经过变换后,可以直接套用针孔相机模型
3 畸变
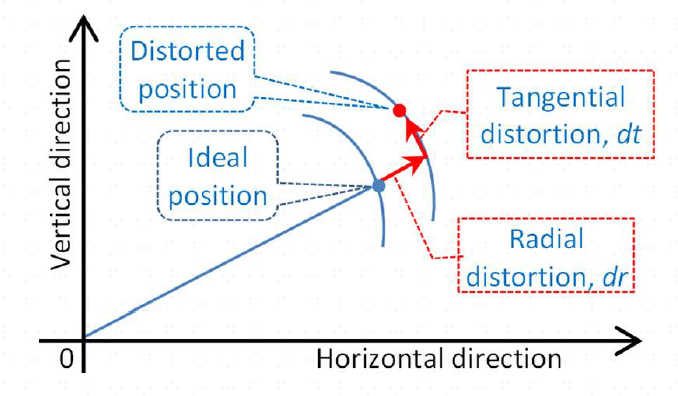
畸变包括径向畸变(Radial Distortion)和切向畸变(Tangential Distortion)
鱼眼相机本质是利用了相机的畸变获取无穷远处的投影,主要是径向畸变
3.1 适用针孔和MEI
首先来看下去畸变的本质,如图所示,一共是四步
① 相机坐标系下某一点,是投影到光心矢量射线(相机成像原理),与图像产生交点。归一化这个坐标(如果再乘以焦距就是图像坐标系上的坐标了),获取畸变的
xy。(这里为什么不乘以f呢,本质是矫正这一条投影到光心的矢量射线,没有本质区别,归一化计算更简单)
② 计算成像半径
r(相机成像半径r理论为r=f*tan(θd),3.2中有提到,也有图)
③ 基于畸变参数,计算去畸变后的
xy,此时,该点再图像坐标系中的位置被矫正
④ 然后基于去畸变后的
xy再变换到像素坐标系下,就可以获取一个矫正的像素坐标
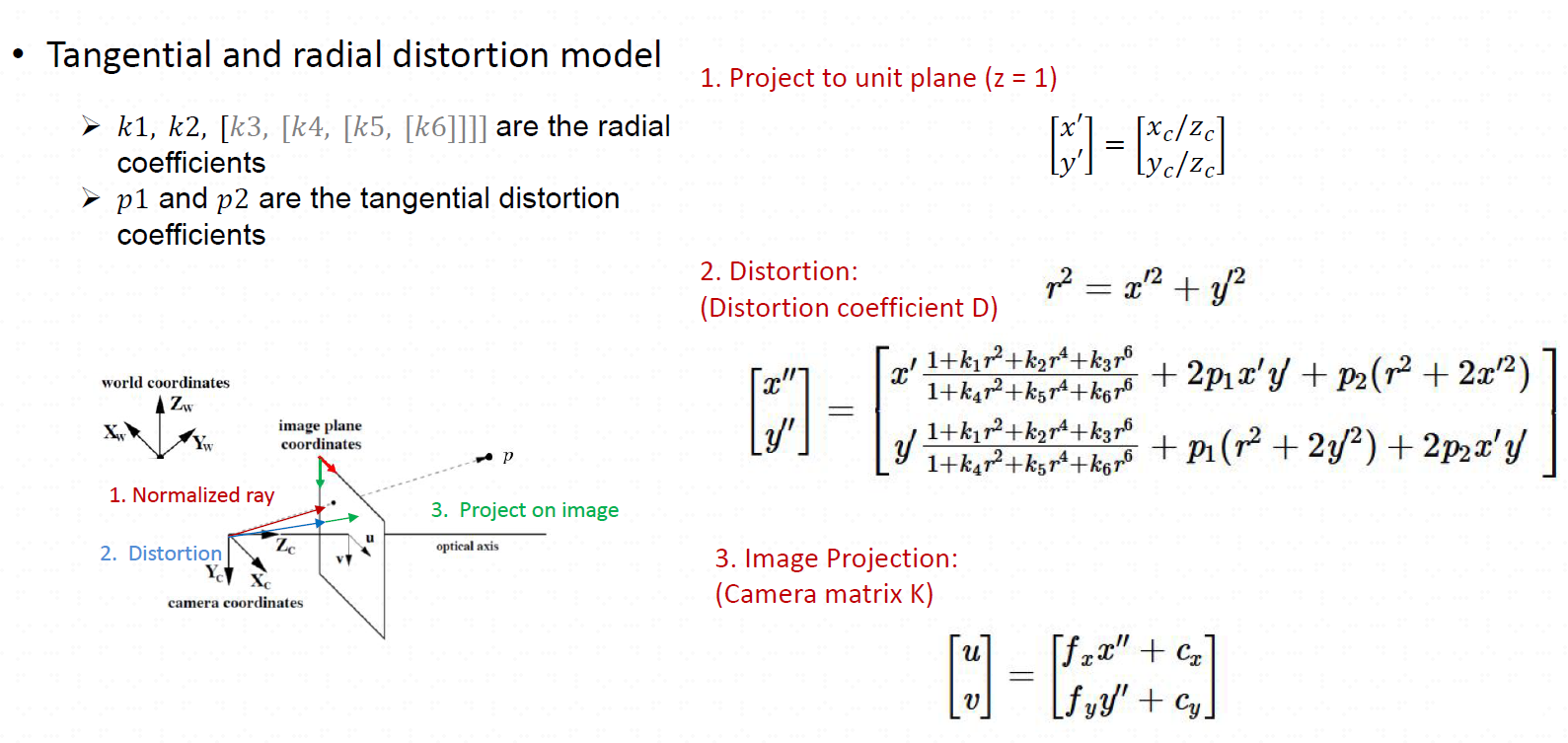
但是实际上,我们只知道像素坐标,而非相机系坐标!所以实际中将像素坐标反变换到相机坐标系(归一化),然后就可以按照这里的去畸变流程处理了。
opencv中的MEI描述
3.2 Kannala-Brandt鱼眼模型
参考opencv,注意,通用模型不是上面哪些等距模型,和哪些完全没关系
相机系
Xc=RX+tXc = RX + t Xc=RX+t
把相机系坐标单独取出来
x=Xc1y=Xc2z=Xc3x = Xc_1\\ y = Xc_2\\ z = Xc_3 x=Xc1y=Xc2z=Xc3
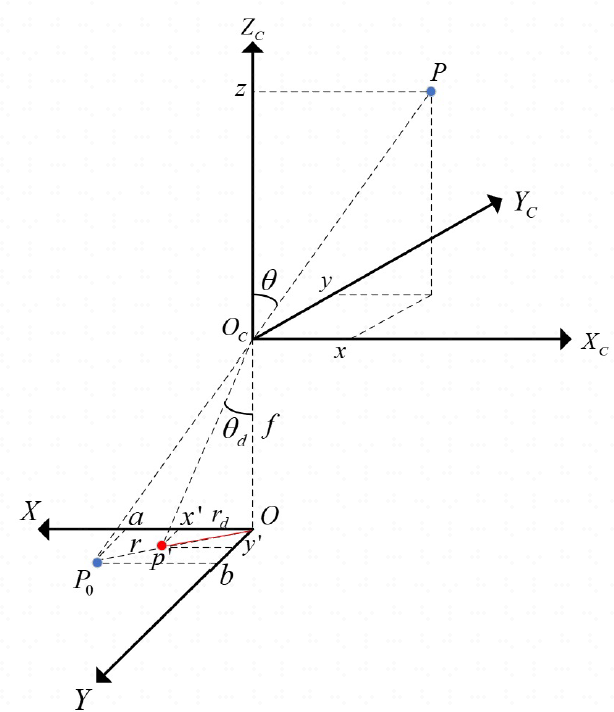
归一化,计算成像半径、夹角
a=xzandb=yzr2=a2+b2θ=arctan(r/1)a = \frac{x}{z} \quad \text{and} \quad b = \frac{y}{z} \quad r^2 = a^2 + b^2 \quad \theta = \arctan(r/1) a=zxandb=zyr2=a2+b2θ=arctan(r/1)
去畸变,注意这里的θdr\frac{\theta_d}{r}rθd实际代码是rdr\frac{r_d}{r}rrd获取的一个比例关系,
opencv给出的公式有点误导,可以参考原始论文(成像半径rd=f∗tan(θd)≈f∗θdr_{d} = f*tan(\theta_{d}) ≈ f* \theta_{d}rd=f∗tan(θd)≈f∗θd,归一化,取f=1,tanx在x接近0时候约等于x)
θd=θ(1+k1θ2+k2θ4+k3θ6+k4θ8)x′=(θdr)ay′=(θdr)b\theta_d = \theta (1 + k_1 \theta^2 + k_2 \theta^4 + k_3 \theta^6 + k_4 \theta^8) \\ x' = \left(\frac{\theta_d}{r}\right) a \\ y' = \left(\frac{\theta_d}{r}\right) b θd=θ(1+k1θ2+k2θ4+k3θ6+k4θ8)x′=(rθd)ay′=(rθd)b
获取去畸变后的像素坐标(
α是偏斜系数,默认为0)
u=fx(x′+αy′)+cxv=fyy′+cyu = f_x (x' + \alpha y') + c_x \\ v = f_y y' + c_y u=fx(x′+αy′)+cxv=fyy′+cy
注:通过上述模型,也就是棋盘格标定得到的去畸变图像,相对于原图,会小很多!距离中心越远的区域,拉伸会很严重,校正后会被切除
4 代码实现
可以参考opencv中映射矩阵来实现
bool UnDistortMap()
{if(is_init){return true;}// 畸变映射,每一张图像的畸变映射是一致的cv::fisheye::initUndistortRectifyMap(mK, mD, cv::Matx33d::eye(), mK,cv::Size(Width, Height), CV_16SC2, m_undistortMapX, m_undistortMapY);// 通过调整cx,cy来增大去畸变后的视野// cv::fisheye::initUndistortRectifyMap(mK, mD, cv::Matx33d::eye(), mK,// cv::Size(mK.at<double>(0,2), mK.at<double>(1,2)), CV_16SC2, // m_undistortMapX, m_undistortMapY); // 或者直接把fxfy调小,缩小相机焦距,视野变大了(分辨率dx不变) if (m_undistortMapX.empty() || m_undistortMapY.empty()) {std::cerr << "Failed to compute undistort maps!" << std::endl;return false;}else{}is_init = true;return true;
}bool undistortImage(const cv::Mat& src, cv::Mat& dst)
{if(!is_init)return false;cv::remap(src, dst, m_undistortMapX, m_undistortMapY, cv::INTER_LINEAR); // 去畸变return true;
}
Computes undistortion and rectification maps for image transform by cv::remap(). If D is empty zero distortion is used, if R or P is empty identity matrixes are used.Parameters:
K – Camera matrix \f$K = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{_1}.
D – Input vector of distortion coefficients k_1, k_2, k_3, k_4).
R – Rectification transformation in the object space: 3x3 1-channel, or vector: 3x1/1x3 1-channel or 1x1 3-channel
P – New camera matrix (3x3) or new projection matrix (3x4)
size – Undistorted image size.
m1type – Type of the first output map that can be CV_32FC1 or CV_16SC2 . See convertMaps() for details.
map1 – The first output map.
map2 – The second output map.




)








——深度学习的数学原理)



】哈希表——242.有效的字母异位词、349.两个数组的交集、202.快乐数、1.两数之和)

