接着上回的话题，在标准齿轮中，我们追求的是“节圆与分度圆重合”的理想状态。但当实际工程提出更苛刻的要求时，比如：

• 需要避免齿轮根切（齿数过少时）。

• 要配凑一个非标准的中心距。

• 需要大幅提高小齿轮的强度和耐磨性。

• 想让两齿轮的寿命接近

在标准齿轮基础上，工程师会通过 “变位”（切削时让刀具偏离齿轮中心）调整齿厚，解决小齿数齿轮 “根切”（齿根被过多切削导致强度降低）或优化传动性能 —— 这就是变位齿轮。这个看似微小的操作，却深刻地改变了齿轮的啮合特性。

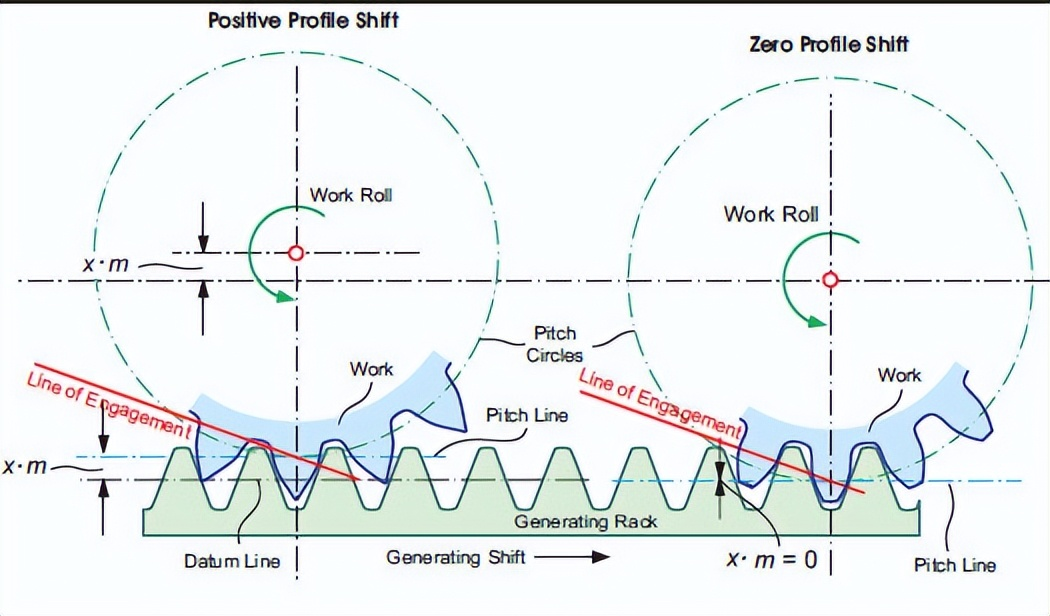
一、先明确：变位齿轮的 3 个核心前提

在分析三者关系前，必须先记住变位齿轮的 “不变量” 和 “可变量”，避免和标准齿轮混淆：

分度圆永远固定，与变位无关

变位只是改变齿的厚度（正变位齿变厚，负变位齿变薄），但齿轮的 “身份基准”—— 分度圆直径，依然由模数（m）和齿数（z）决定，公式还是 d = m×z。哪怕把齿轮切得再 “胖” 或再 “瘦”，只要模数和齿数不变，分度圆就不会变。

中心距由 “变位系数之和” 决定

标准齿轮的中心距是 a = (d₁ + d₂)/2（d₁、d₂为两齿轮分度圆直径）；而变位齿轮的中心距要考虑 “变位系数”（x₁、x₂，正变位为正，负变位为负），公式变为：

a’ = a + y×m

其中 y = x₁ + x₂（变位系数之和），y 是关键：

若 y=0（等变位，x₁=-x₂）：中心距 a’=a，和标准齿轮一样；

若 y>0（正变位之和，x₁+x₂>0）：中心距 a’>a，比标准大；

若 y<0（负变位之和，x₁+x₂<0）：中心距 a’<a，比标准小。

节圆仍由 “实际中心距” 决定，与分度圆的关系随 a’ 变

和标准齿轮一样，变位齿轮的节圆是啮合时的 “实际工作圆”，直径由中心距 a’ 和齿数比决定（因为传动比 i=z₂/z₁=d₂’/d₁’，d₁’、d₂’ 为节圆直径）。因此：

当 a’=a（y=0）：节圆直径 d₁’=d₁、d₂’=d₂，节圆与分度圆重合；

当 a’≠a（y≠0）：节圆直径偏离分度圆，a’ 越大，d₁’、d₂’ 越大；a’ 越小，d₁’、d₂’ 越小。

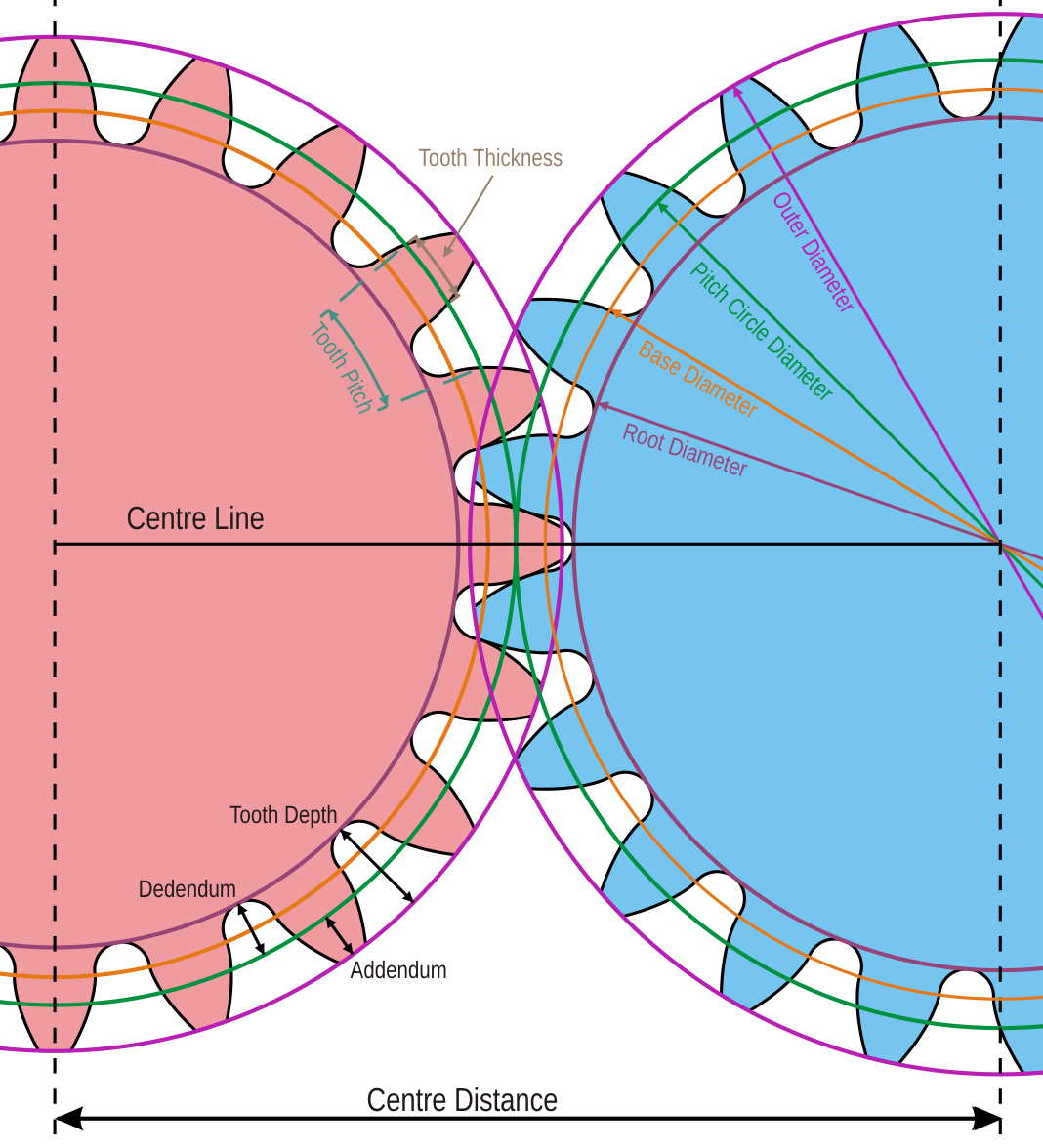
二、实际例子：用具体参数算清三者关系

我们选一组典型参数，分 “等变位” 和 “不等变位” 两种情况，直观看三者变化：

已知基础参数

模数 m=2mm（齿的大小）；

小齿轮 1：齿数 z₁=15（易根切，需正变位），分度圆 d₁=m×z₁=2×15=30mm；

大齿轮 2：齿数 z₂=40，分度圆 d₂=m×z₂=2×40=80mm；

标准中心距 a=(d₁+d₂)/2=(30+80)/2=55mm。

情况 1：等变位（y=0，解决小齿轮根切）

为避免小齿轮 z₁=15 根切，取小齿轮正变位 x₁=+0.2，大齿轮负变位 x₂=-0.2（变位系数之和 y=0.2-0.2=0）。

中心距 a’：按公式 a’=a+y×m=55+0×2=55mm（和标准中心距相同）；

节圆直径：因传动比 i=z₂/z₁=40/15=8/3，且 d₁’+d₂’=2a’=110mm（节圆之和是中心距的 2 倍）。

设 d₁’=x，则 d₂’=(8/3) x，代入得：x + (8/3) x = 110 → x=30mm，d₂’=80mm；

三者关系：

分度圆 d₁=30mm、d₂=80mm（固定）；

中心距 a’=55mm（和标准相同）；

节圆 d₁’=30mm、d₂’=80mm（与分度圆完全重合）。

→ 结论：等变位齿轮（y=0）时，中心距不变，节圆与分度圆重合，既解决了小齿轮根切，又保持了标准安装状态。

情况 2：不等变位（y>0，需增大中心距）

若实际安装空间需要中心距 56mm（比标准大 1mm），可调整变位系数：取 x₁=+0.3，x₂=+0.2（变位系数之和 y=0.3+0.2=0.5）。

中心距 a’：按公式 a’=a+y×m=55+0.5×2=56mm（刚好满足安装需求）；

节圆直径：传动比仍为 i=8/3，d₁’+d₂’=2a’=112mm。

设 d₁’=x，则 d₂’=(8/3) x，代入得：x + (8/3) x = 112 → x=31.636mm，d₂’=80.364mm；

三者关系：

分度圆 d₁=30mm、d₂=80mm（依然固定，没变位影响）；

中心距 a’=56mm（因 y>0，比标准大 1mm）；

节圆 d₁’≈31.64mm（>30mm）、d₂’≈80.36mm（>80mm）（随中心距增大而偏离分度圆）。

结论：不等变位（y≠0）时，中心距改变，节圆同步偏离分度圆，但传动比（8/3≈2.67）始终不变，仍由齿数比决定。

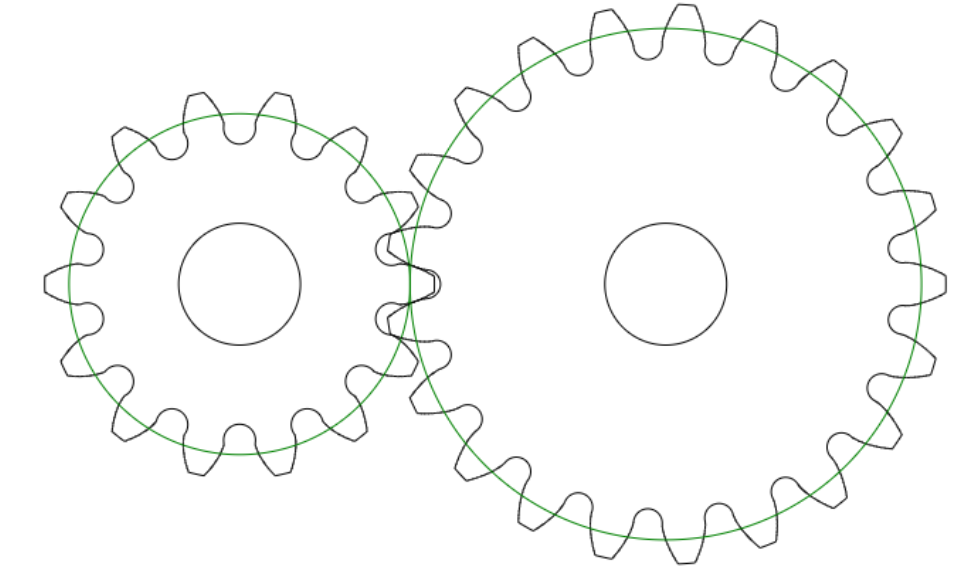
三、总结：变位齿轮三者关系的核心

用一句话概括：分度圆是 “定海神针”（m、z 定，它就定），中心距是 “调节器”（y 定，它就定），节圆是 “跟屁虫”（中心距定，它就定）。

今天就分享到这，感谢您抽出宝贵的时间阅读！