目录
1.深度学习的介绍
2.神经网络的构造
①神经元结构
②神经网络组成
③权重核心性
3.神经网络的本质
4.感知器
单层感知器的局限性:
5.多层感知器
多层感知器的优势:
6.偏置
7.神经网络的设计
8.损失函数
常用的损失函数:
9.softmax交叉熵损失函数
10.正则化惩罚
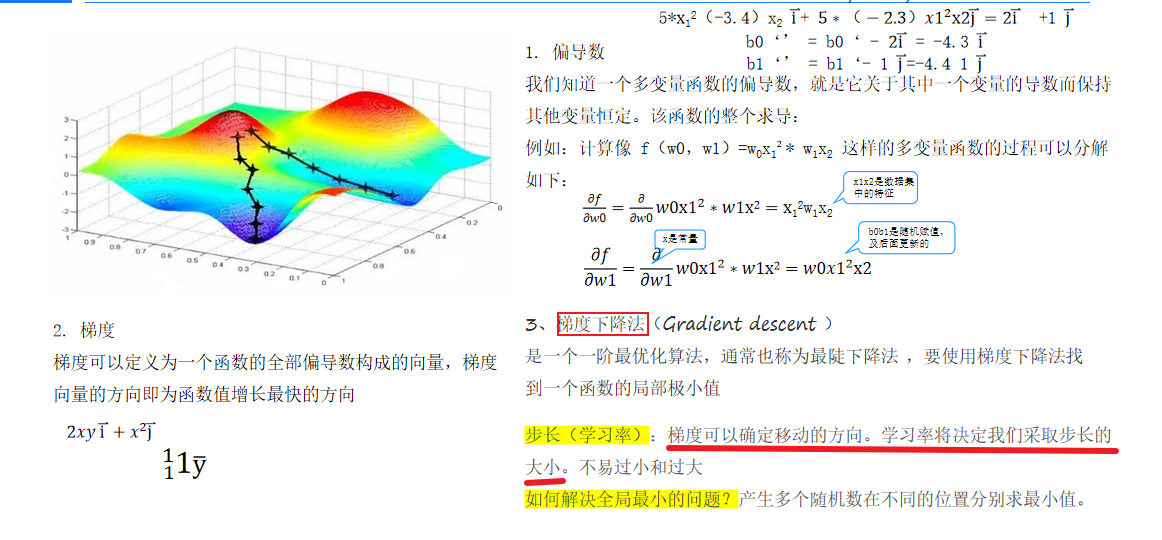
11.梯度下降
12.反向传播
1.深度学习的介绍
深度学习(DL, Deep Learning)是机器学习(ML, Machine Learning)领域中一个新的研究方向。

2.神经网络的构造
①神经元结构
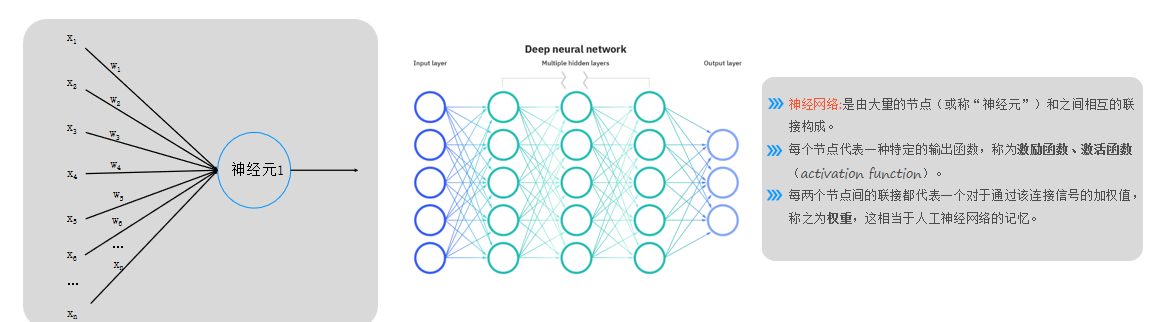
- 单个神经元模拟逻辑回归,输入信号(如图片数据)通过权重(ω)加权求和后,经激活函数(如Sigmoid)输出结果(0或1)。
- 输入层(蓝色)仅表示输入数据,非神经元;输出层(蓝色末端)为最终结果。
②神经网络组成
- 由大量神经元(节点)及连接线构成,每个节点代表一种特定的输出函数,每层神经元按列排列,信号仅传递至下一层(无跨层或同层连接)。
- 激活函数(如Sigmoid)用于非线性映射,当前阶段默认使用Sigmoid,后续会引入其他函数。
③权重核心性
- 权重(ω)是神经网络的关键记忆单元,模型训练的核心是求解权重值而非神经元本身。
3.神经网络的本质
通过参数与激活函数来拟合特征与目标之间的真实函数关系。但在一个神经网络的程序中,不需要神经元和线,本质上是矩阵的运算,实现一个神经网络最需要的是线性代数库。
4.感知器
有一层神经元组成的神经网络叫做感知器,只能划分线性数据

单层感知器的局限性:
- 单层感知器仅能处理线性分类问题(如用直线划分数据),无法解决非线性分类(如圆形或复杂曲线分布的数据)。
5.多层感知器
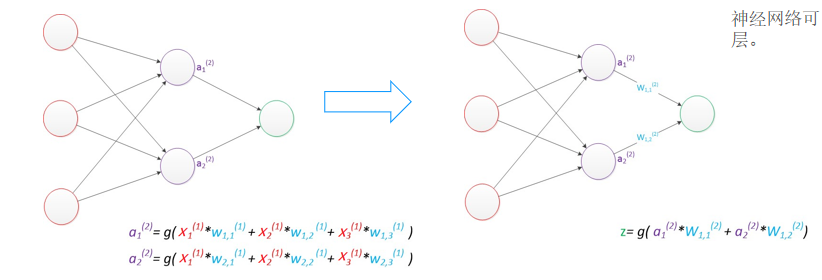
增加了一个中间层,即隐含层(神经网络可以做到非线性划分的关键)
多层感知器的优势:
- 引入隐含层后,通过多次非线性激活函数(如
sigmoid)实现数据“弯曲”,从而处理非线性分类问题。 - 示例:
- 隐含层神经元数为1时,输出为一条直线;
- 神经元数增至2或3时,可生成弯曲的决策边界(如近似三角形或弧形),提升分类能力。
- 核心原理:前向传播中,每层输出经激活函数映射,叠加非线性特性。
6.偏置
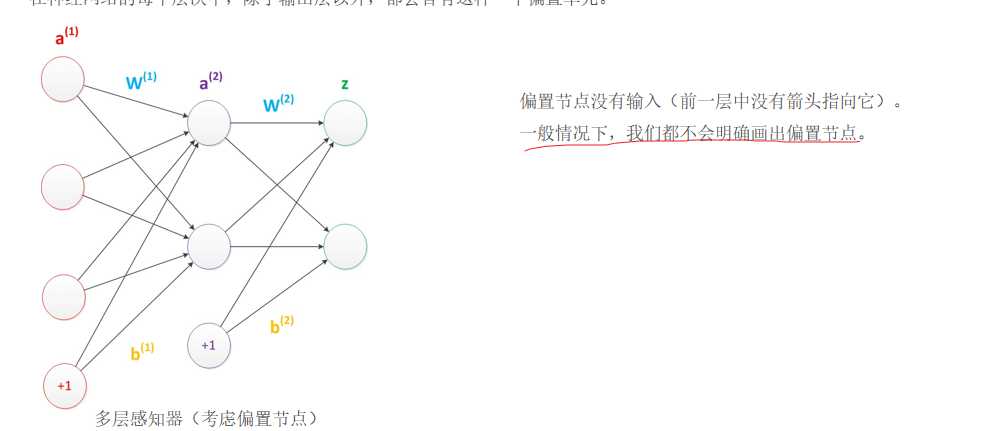
在神经网络中需要默认添加偏置神经元(节点),它本质上是一个只含有存储功能,且存储值永远为1的单元。 在神经网络的每个层次中,除了输出层以外,都会含有这样一个偏置单元。
7.神经网络的设计
输入层的节点数:与特征的维度匹配
输出层的节点数:与目标的维度匹配。
中间层的节点数:目前业界没有完善的理论来指导这个决策。一般是根据经验来设置。较好的方法就是预先设定几个可选值,通过切换这几个值来看整个模型的预测效果,选择效果最好的值作为最终选择。

8.损失函数
首先我们需要知道我们训练模型的目的是使得参数尽可能的与真实的模型逼近。
具体做法:
1、首先给所有参数赋上随机值。我们使用这些随机生成的参数值,来预测训练数据中的样本。 2、计算预测值为yi,真实值为y。那么,定义一个损失值loss,损失值用于判断预测的结果和真实值的误差,误差越小越好。
常用的损失函数:
0-1损失函数(二分类)
均方差损失
平均绝对差损失
交叉熵损失(分类)
合页损失
9.softmax交叉熵损失函数
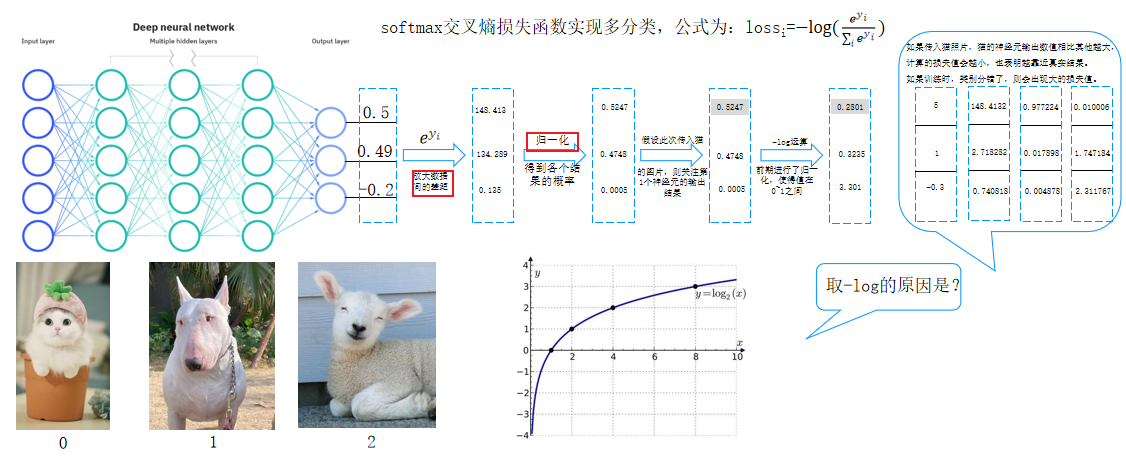
softmax交叉熵损失函数实现多分类,公式为:lossi=−log(e^y_i/∑_ie^y_i)
- 输出层通过Softmax处理:
- 对神经元输出值进行指数级放大(如e^{0.5}),拉大概率差异。
- 归一化后得到各类别概率占比(总和为1)。
- 损失计算:
- 根据真实标签选择对应神经元的输出概率。
- 通过负对数运算(-log(p))计算损失值:概率越接近1,损失越小;概率越低,损失越大。
- 多分类任务需对多张图片的损失求平均值。
10.正则化惩罚
正则化惩罚的功能:主要用于惩罚权重参数w,一般有L1和L2正则化。
- 为防止过拟合和选择更均衡的ω,损失函数需加入正则化项(如L1、L2正则化)。
- 正则化惩罚项的值随ω的不均衡性增大而增大,促使模型选择更均衡的参数
例如:
均方差损失函数:loss = 1/N∑_i=1^N(yp − y)2+λR(W)
输入为:x = [1,1,1,1]现有2种不同的权重值,
w1 = [1,0,0,0],w2 = [0.25,0.25,0.25,0.25]
w1和w2与输入的乘积都为1,但w2 与每一个输入数据进行计算后都有数据,使得w2会学习到每一个特征信息。而w1只和第1个输入信息有关系,容易出现过拟合现象,因此w2的效果会比w1 好

11.梯度下降
梯度下降算法用于求解损失函数的极小值,通过计算损失函数对每个ω的偏导数确定下降方向
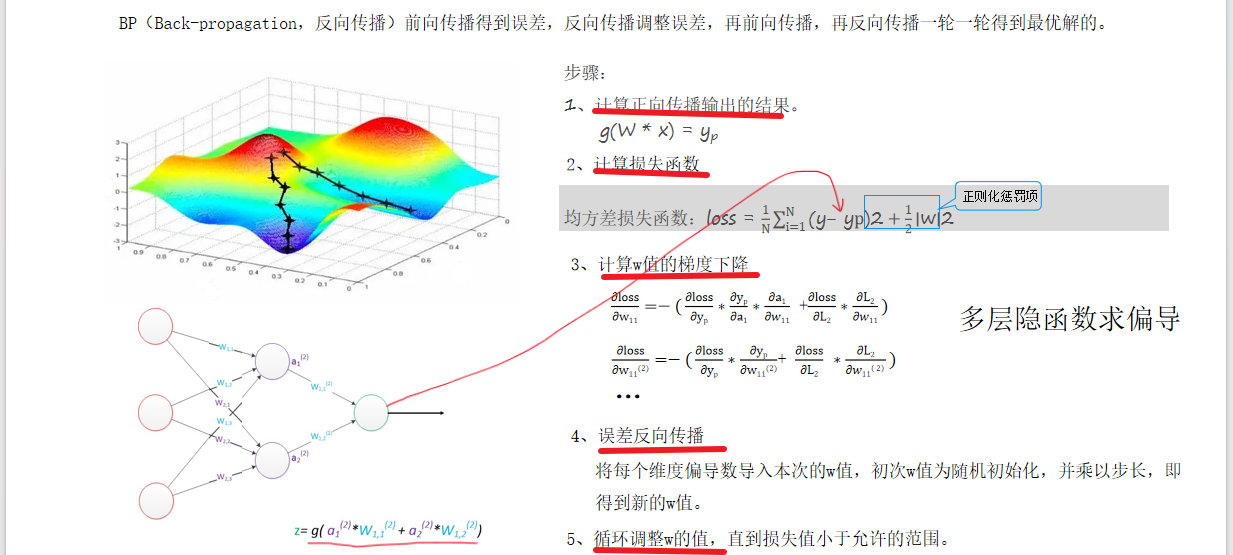
12.反向传播
BP(Back-propagation,反向传播)前向传播得到误差,反向传播调整误差,再前向传播,再反向传播一轮一轮得到最优解的。
- 反向传播通过损失函数计算梯度,反向更新ω值,分为以下步骤:
- 随机初始化ω。
- 前向传播计算预测值(YP)和损失。
- 对每个ω求偏导(链式法则),代入当前ω值得到梯度方向。
- 根据学习率更新ω,迭代至收敛。
- 深层网络中,偏导计算因隐函数嵌套变得复杂(如30层网络需29次链式求导)。
)












)
)




与同义词治理)