二叉树 - LeetCode 94. 二叉树的中序遍历（简单）
二叉树 - LeetCode 104. 二叉树的最大深度（简单）
二叉树 - LeetCode 226. 翻转二叉树（简单）
二叉树 - LeetCode 101. 对称二叉树（简单）
二叉树 - LeetCode 543. 二叉树的直径（简单）

二叉树 - LeetCode 94. 二叉树的中序遍历（简单）

【题目描述】

给定一个二叉树的根节点 root，返回它的中序遍历。

【示例 1】

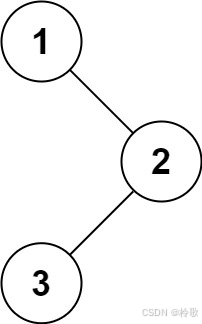
在这里插入图片描述

输入：root = [1,null,2,3]
输出：[1,3,2]

【示例 2】

输入：root = []
输出：[]

【示例 3】

输入：root = [1]
输出：[1]

【提示】

树中节点数目在范围 $[0, 100]$ 内
$- 100 <= N o d e . v a l <= 100$

进阶：递归算法很简单，你可以通过迭代算法完成吗？

【分析】

递归遍历二叉树非常简单，不理解的可以看树和图的遍历方式详解：【UCB CS 61B SP24】Lecture 22 & 23: Tree and Graph Traversals, DFS, BFS。

本题的 Tips 中提到尝试用迭代算法完成，那么分析一下如何不用递归实现中序遍历。

对于每个节点，如果其左子树存在，就需要先遍历左子树，但是当前点也不能扔掉，因为遍历完左子树还要回来遍历当前节点，因此如果当前节点有左子树就先将当前点压入栈中。

如果当前节点的左子树已经遍历完了，就可以遍历自身了，遍历完就可以出栈，如果有右子树，那么就对右子树继续执行相同的操作遍历，如果没有右子树就可以出栈下一个节点，也就是当前节点的父节点。

【代码】

【递归方法】

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> res;vector<int> inorderTraversal(TreeNode* root) {if (!root) return res;if(root->left) inorderTraversal(root->left);res.push_back(root->val);if (root->right) inorderTraversal(root->right);return res;}
};

【迭代方法】

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> res;stack<TreeNode*> stk;while (root || stk.size()) {  // 当前节点不为空或栈不为空时循环操作while (root) {  // 一直走到没有左子树为止stk.push(root);root = root->left;}root = stk.top();  // root 为空时说明栈顶元素可以被遍历了stk.pop();res.push_back(root->val);root = root->right;  // 如果没有右子树 root 就为空，下一次出栈的就是 root 的父节点}return res;}
};

二叉树 - LeetCode 104. 二叉树的最大深度（简单）

【题目描述】

给定一个二叉树 root，返回其最大深度。

二叉树的最大深度是指从根节点到最远叶子节点的最长路径上的节点数。

【示例 1】

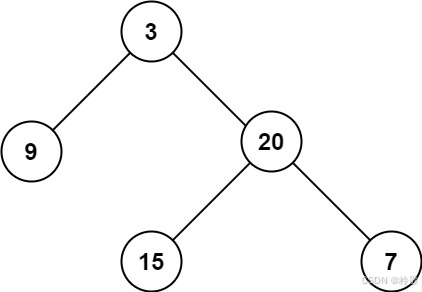
在这里插入图片描述

输入：root = [3,9,20,null,null,15,7]
输出：3

【示例 2】

输入：root = [1,null,2]
输出：2

【提示】

树中节点的数量在 $0, 10^4]$ 区间内。
$- 100 <= N o d e . v a l <= 100$

【分析】

用 BFS 也就是类似前两题的做法能够求出层数，也可以直接用递归求解，从根节点往下递归求解每个节点的高度，到空节点了高度就为 0，否则当前节点的高度就是左子树与右子树中的最大高度加一（当前节点的高度比子树多 1）。

【代码】

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int maxDepth(TreeNode* root) {  // 返回 root 的最大高度if (!root) return 0;return max(maxDepth(root->left), maxDepth(root->right)) + 1;}
};

二叉树 - LeetCode 226. 翻转二叉树（简单）

【题目描述】

给你一棵二叉树的根节点 root，翻转这棵二叉树，并返回其根节点。

【示例 1】

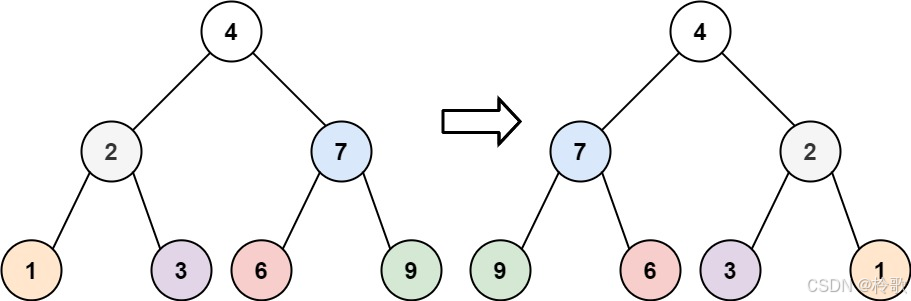
在这里插入图片描述

输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

【示例 2】

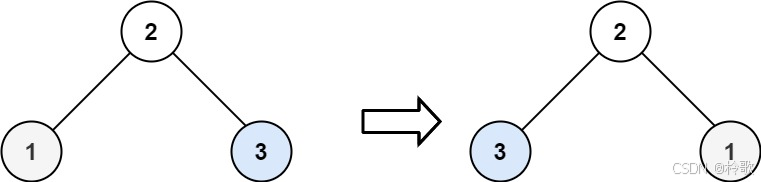
在这里插入图片描述

输入：root = [2,1,3]
输出：[2,3,1]

【示例 3】

输入：root = []
输出：[]

【提示】

树中节点数目范围在 $[0, 100]$ 内
$- 100 <= N o d e . v a l <= 100$

【分析】

从根节点开始递归地处理每个结点，将每个结点的左右子树交换一下即可。

【代码】

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* invertTree(TreeNode* root) {if (!root) return nullptr;swap(root->left, root->right);invertTree(root->left);invertTree(root->right);return root;}
};

二叉树 - LeetCode 101. 对称二叉树（简单）

【题目描述】

给你一个二叉树的根节点 root，检查它是否轴对称。

【示例 1】

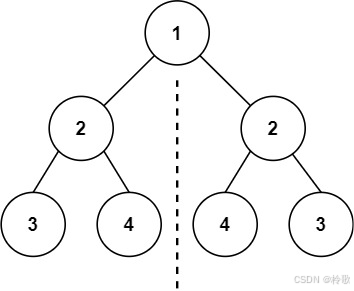
在这里插入图片描述

输入：root = [1,2,2,3,4,4,3]
输出：true

【示例 2】

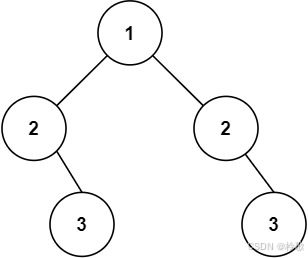
在这里插入图片描述

输入：root = [1,2,2,null,3,null,3]
输出：false

【提示】

树中节点数目在范围 $[1, 1000]$ 内
$- 100 <= N o d e . v a l <= 100$

进阶：你可以运用递归和迭代两种方法解决这个问题吗？

【分析】

对称的树具有以下属性之一：

左右子节点均为空；
左右子节点的值相同，且左子节点的左子树与右子节点的右子树相同，左子节点的右子树与右子节点的左子树相同。

因此我们可以递归判断左右子树是否对称。

题目提到用递归和迭代实现，那么如何用迭代实现？

可以用队列维护对称的相对关系，首先将根节点的左右子节点入队，然后不断循环每次从队列中取两个节点，判断这两个节点是否对称，然后将其中一个节点的左/右子节点与另一个节点的右/左子节点对应成两组分别加入到队列中，如果队列为空遍历完整棵树还没发现非对称的节点说明整棵树就是对称的。

【代码】

【递归方法】

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool isSymmetric(TreeNode* root) {return dfs(root->left, root->right);}bool dfs(TreeNode* l, TreeNode* r) {if (!l && !r) return true;  // 两个节点均为空if (!l || !r || l->val != r->val) return false;  // 只有一个节点为空或两个节点值不同return dfs(l->left, r->right) && dfs(l->right, r->left);  // 左节点的左/右子树要和右节点的右/左子树对称}
};

【迭代方法】

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool isSymmetric(TreeNode* root) {queue<TreeNode*> Q;Q.push(root->left), Q.push(root->right);while (!Q.empty()) {auto p = Q.front(); Q.pop();auto q = Q.front(); Q.pop();if (!p && !q) continue;if (!p || !q || p->val != q->val) return false;  // 不对称Q.push(p->left), Q.push(q->right);  // p 的左子节点需要和 q 的右子节点对称Q.push(p->right), Q.push(q->left);  // p 的右子节点需要和 q 的左子节点对称}return true;  // 全遍历完了说明树是对称的}
};

二叉树 - LeetCode 543. 二叉树的直径（简单）

【题目描述】

给你一棵二叉树的根节点，返回该树的直径。

二叉树的直径是指树中任意两个节点之间最长路径的长度。这条路径可能经过也可能不经过根节点 root。

两节点之间路径的长度由它们之间边数表示。

【示例 1】

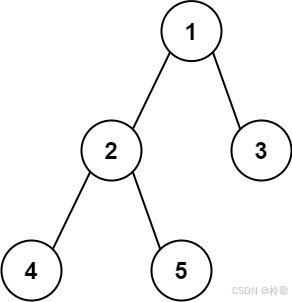
在这里插入图片描述

输入：root = [1,2,3,4,5]
输出：3
解释：3 ，取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。

【示例 2】

输入：root = [1,2]
输出：1

【提示】

树中节点数目在范围 $1, 10^4]$ 内
$- 100 <= N o d e . v a l <= 100$

【分析】

我们递归枚举每个点作为路径的最高点，那么这条路径的长度为该结点往左子树走的最大长度加上往右子树走的最大长度，因此可以在递归的时候维护每个结点往下走到叶子结点的最大长度，这样就能快速获得当前结点左右子树往下走的最大长度。

如果是多叉树求树的直径有通用解法（求图的最长路径），首先任选一个点作为根结点，通过 DFS 找到最远的结点，然后再将其作为根节点，通过 DFS 找到最远的点，这段距离就是最长路径。

【代码】

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int res;int dfs(TreeNode* root) {  // 返回从 root 往下走的最长长度if (!root) return 0;int l = dfs(root->left), r = dfs(root->right);res = max(res, l + r);return max(l, r) + 1;}int diameterOfBinaryTree(TreeNode* root) {dfs(root);return res;}
};