为什么需要批量规范化层呢？

让我们来回顾一下训练神经网络时出现的一些实际挑战：

首先，数据预处理的方式通常会对最终结果产生巨大影响。回想一下我们应用多层感知机来预测房价的例子。使用真实数据时，我们的第一步是标准化输入特征，使其平均值为0，方差为1。直观地说，这种标准化可以很好地与我们的优化器配合使用，因为它可以将参数的量级进行统一。
第二，对于典型的多层感知机或卷积神经网络，当我们训练时，中间层中的变量（例如，多层感知机中的仿射变换输出）可能具有更广的变化范围：不论是沿着从输入到输出的层，跨同一层中的单元，或是随着时间的推移，模型参数的随着训练更新变幻莫测。批量规范化的发明者非正式地假设，这些变量分布中的这种偏移可能会阻碍网络的收敛。直观地说，我们可能会猜想，如果一个层的可变值是另一层的100倍，这可能需要对学习率进行补偿调整。
第三，更深层的网络很复杂，容易过拟合。这意味着正则化变得更加重要。

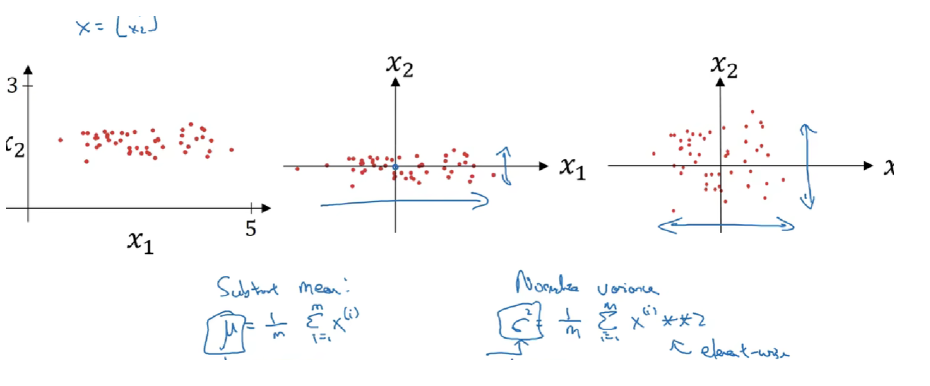
批量规范化应用于单个可选层（也可以应用到所有层），其原理如下：

在每次训练迭代中，我们首先规范化输入，即通过减去其均值并除以其标准差，其中两者均基于当前小批量处理。接下来，我们应用比例系数和比例偏移。正是由于这个基于批量统计的标准化，才有了批量规范化的名称。

BatchNorm 在一个 batch 的同一通道内做归一化
LayerNorm 在每条样本的所有通道/特征内做归一化

作用：把输入分布强行压成零均值、单位方差，减轻 Internal Covariate Shift 内部协变量偏移，使优化曲面更平滑，从而让梯度更稳定、训练更快、更易收敛到较优的泛化解。

计算例子

下面用 3×4 的 RGB 小批次张量举例，并给出计算过程与差异对照：

数据形状约定：设输入 x 形状为 (B, C, H, W) = (2, 3, 2, 2)：

2 张图片
3 个通道 (R, G, B)
每通道 2×2 像素

把每张图片展平后，张量变成：

batch0-0R: [[1, 3], [5, 7]]    → 4 个标量 1 3 5 7G: [[2, 4], [6, 8]]    → 2 4 6 8B: [[0, 2], [4, 6]]    → 0 2 4 6batch0-1R: [[2, 4], [6, 8]]G: [[3, 5], [7, 9]]B: [[1, 3], [5, 7]]

BatchNorm 的计算：BN是在同一个batch中不同样本之间的同一位置的神经元之间进行归一化。

归一化维度：在 (B, H, W) 三个维度上求均值/方差，每个通道一组统计量。
以 R 通道为例：共有 2×2×2 = 8 个像素值：{1, 3, 5, 7, 2, 4, 6, 8}
- μ_R = (1+3+5+7+2+4+6+8)/8 = 4.5
- σ²_R = 平均((x−4.5)²) = 5.25
归一化后每个像素先做 (x−μ)/√(σ²+ε)，再进行 γ·x + β 的仿射。 G、B 通道同理，各自独立拥有一组 μ、σ、γ、β。
参数：每个通道一对 (γ, β)，共 3×2 = 6 个可学习标量。
推理阶段：用滑动平均保存的全局 μ、σ，不再依赖 batch。

LayerNorm 的计算：LN是在同一个样本中不同神经元之间进行归一化。

归一化维度：在 (C, H, W) 三个维度上求均值/方差，每条样本一组统计量。
以 batch-0 为例：把 3×2×2 = 12 个数拉成一条向量： {1, 3, 5, 7, 2, 4, 6, 8, 0, 2, 4, 6}
- μ = 4.0
- σ² = 平均((x−4)²) = 5.0
归一化后再用该样本独有的 γ、β 做仿射。 batch-1 同理，用 batch-1 自己的 12 个数重新算 μ、σ。
参数：每条样本一对 (γ, β)，可共享或不共享，与 BatchNorm 不同。

为什么有效？

输入：手写数字灰度图，只保留 2 个像素 → 输入 x 形状 (batch, 2)。
网络：2 层线性 y = W₂ ReLU(W₁x)。
任务：二分类 0/1，用 Sigmoid + BCE 损失。
假设 batch = 4，像素值如下（故意把范围拉大）：
```
x = [[200, 190],[10,  5],[180, 170],[8,   4]]
```
真实标签 y = [0, 1, 0, 1]

没有归一化时（裸网络）

第一层输出 z₁ = W₁x，假设 W₁ 随机初始化后， z₁ 的均值≈180，方差≈6000。
经过 ReLU 后，大多数值落在 0 或 >100 的区间 → 梯度在反向传播时： – 很大值那一端 → 梯度爆炸； – 很多 0 → 梯度消失。 结果：Loss 震荡剧烈，训练 10 个 epoch 仍降不下来。

加上 BatchNorm（放在第一层之后）：

计算 batch 内每个通道的均值 μ、方差 σ²：
- μ₁ = (200+10+180+8)/4 = 99.5
- μ₂ = (190+5+170+4)/4 = 92.25
归一化：
- ẑ₁ = (z₁ − μ₁)/√(σ₁²+ε)
- ẑ₂ = (z₂ − μ₂)/√(σ₂²+ε)
现在所有值缩放到 ≈[-1,1] 区间。
再乘可学习 γ、β 做仿射，保持表达能力。
效果：
- 第一层输出方差≈1，ReLU 后的分布不再极端。
- 反向传播时梯度大小稳定，loss 单调下降，3 个 epoch 就收敛。

加上 LayerNorm（放在第一层之后）

对每条样本的所有特征一起算 μ、σ²：
- 样本 0：μ = (200+190)/2 = 195
- 样本 1：μ = (10+5)/2 = 7.5
- …………
每条样本内部做 (x−μ)/σ，再 γ、β。
- 效果：
  - 即使 batch 大小变成 1 也能用（LN 不依赖 batch）。
  - 输入尺度被拉齐，梯度同样稳定，收敛速度与 BN 相近。

比较点	BatchNorm	LayerNorm
归一化范围	跨 batch 的同一通道	单条样本内的全部特征
均值/方差维度	(B, H, W)	(C, H, W)
依赖 batch 大小	是（推理时用滑动平均）	否
典型场景	CNN、大 batch	RNN、Transformer、小 batch
参数量	每通道一对 γβ	每层/每样本一对 γβ