1. 导读

大型语言模型（Large Language Models, LLMs）在自主决策场景中的应用日益广泛，它们需要在庞大的行动空间中进行响应采样（response sampling）。然而，驱动这一采样过程的启发式机制仍缺乏深入研究。本文系统分析了 LLM 的采样行为，并发现其底层机制与人类决策过程存在相似性——由**描述性成分（descriptive component）和规范性成分（prescriptive component）**共同构成。前者反映统计学意义上的常态分布，后者则体现模型内部隐含的“理想值”倾向。

作者通过跨领域（如公共健康、经济趋势）的实证分析发现，LLM 的输出往往会从统计常态向规范性理想值发生一致性的偏移，这种模式与人类在“正常性”判断上的倾向高度一致。进一步的案例研究和与人类实验的对比表明，这种采样偏移可能在现实应用中引发显著的决策偏差，甚至带来伦理风险。例如，在医疗场景中，模型可能会将康复时间的预测向理想状态收敛，从而忽略真实分布的长尾风险。

本文的重要贡献在于提出了一种全新的采样理论框架，将 LLM 的输出生成视为“部分描述性、部分规范性”的混合过程。这不仅有助于理解模型的行为机制，也为评估与优化 LLM 在关键任务中的可靠性和公平性提供了理论基础。

论文基本信息

• 论文标题：A Theory of Response Sampling in LLMs: Part Descriptive and Part Prescriptive
• 作者：Sarath Sivaprasad, Pramod Kaushik, Sahar Abdelnabi, Mario Fritz
• 作者单位：
  1. CISPA Helmholtz Center for Information Security
  2. TCS Research, Pune
  3. Microsoft
• 发表会议：ACL 2025（Oral）
• 提交时间：2024年2月16日，v4版本更新于2025年7月9日
• 论文链接：https://arxiv.org/abs/2402.11005

➔➔➔➔点击查看原文，获取更多大模型相关资料

2. 背景与研究动机

2.1 大型语言模型的响应采样背景

大型语言模型（Large Language Models, LLMs）在自主决策、文本生成及多轮交互等任务中，需要在极为庞大的动作空间中进行概率采样，即根据条件概率分布从候选输出中选取最终响应。尽管近年来在生成质量优化、随机性控制以及采样策略（如温度调节、Top-k、Nucleus sampling）等方面取得了显著进展，但驱动这一采样过程的深层机制仍缺乏系统性的理论探讨，导致我们在解释和预测模型行为时存在明显局限。

2.2 人类决策中的双重成分类比

在认知科学领域，人类决策常常同时受到描述性成分（descriptive component）与规范性成分（prescriptive component）的驱动：前者反映经验或统计意义上的常态，例如疾病的平均康复时间；后者则体现理想化或应当达到的目标，例如临床指导中设定的理想康复天数。本文提出，LLMs在响应采样时也展现出类似的双重驱动特性——它们不仅复现训练数据的统计常态，还会向模型内部隐含的理想原型发生系统性偏移。这种偏移可能源自训练数据分布、指令微调目标的优化方向，或模型在语义空间中形成的概念表示。

2.3 现有研究的不足与挑战

当前学界对LLM 响应采样的研究主要集中在优化生成多样性与准确性，但鲜有工作关注描述性与规范性力量在采样过程中的交互机制，也缺乏跨领域的实证研究验证其普适性。这一理论空白导致我们难以预测模型偏移模式，并可能在公共健康、经济预测等高风险领域引发系统性误判与伦理风险。

2.4 本文研究动机

鉴于上述不足，本文旨在提出一个能够统一解释 LLM 响应采样中描述性与规范性成分并存现象的理论框架，并通过跨领域实验系统验证其存在及影响，以期为模型可靠性与公平性提供理论依据和实践参考。

➔➔➔➔点击查看原文，获取更多大模型相关资料

3. 采样理论建模（Sampling Theory Modeling）

3.1 理论框架概述

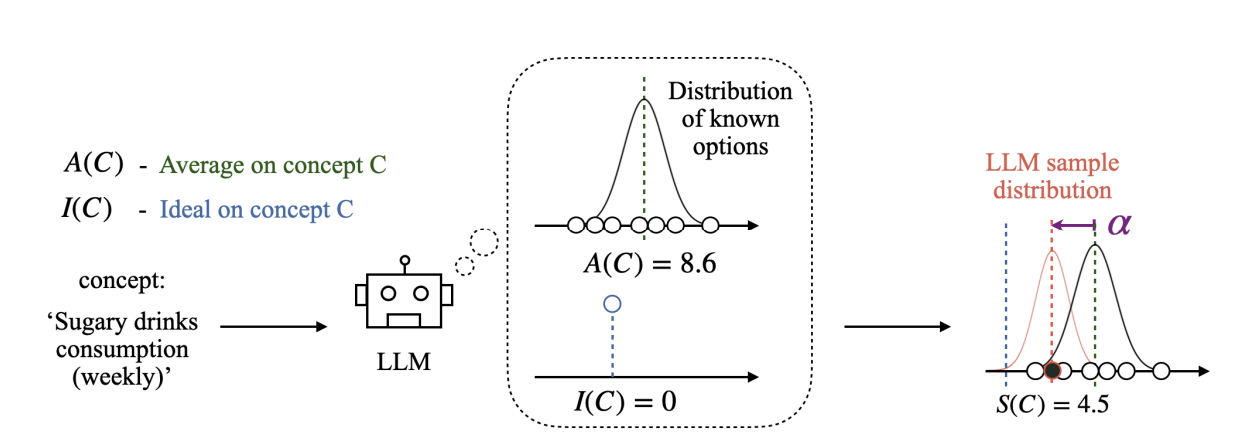
本章提出了一个用于刻画 大型语言模型（LLMs） 在生成过程中的 采样机制 的理论模型。研究发现，LLM 在对一个概念 $C$ 进行采样时，并不仅仅依据 统计分布（Average，记作 $A(C)$），还会受到一种 理想化规范（Ideal，记作 $I(C)$）的影响。这种理想化规范类似于人类认知中的 处方性规范（Prescriptive Norm），会引导模型输出偏向某个“理想值”。因此，模型实际采样的结果 $S(C)$ 往往会偏离真实统计均值，形成系统性的偏移。

---

3.2 数学建模与公式推导

为了量化这种偏移，作者定义了 采样偏移量 $\alpha$：

$$\alpha (C)=I(C)-A(C)$$

在实际采样中，LLM 的输出 $S(C)$ 可以建模为：

$$S(C)=A(C)+\hat{\alpha }\cdot \alpha (C)$$

其中，$\hat{\alpha }$ 是一个归一化系数，用于衡量采样值相对 统计均值 与 理想值 之间的平衡程度：

• 当 $\hat{\alpha }>0$ 时，采样值向理想值方向偏移；
• 当 $\hat{\alpha }=0$ 时，采样值与统计均值一致；
• 当 $\hat{\alpha }<0$ 时，采样值偏离理想值，向相反方向移动。

---

3.3 实验图示与结果分析

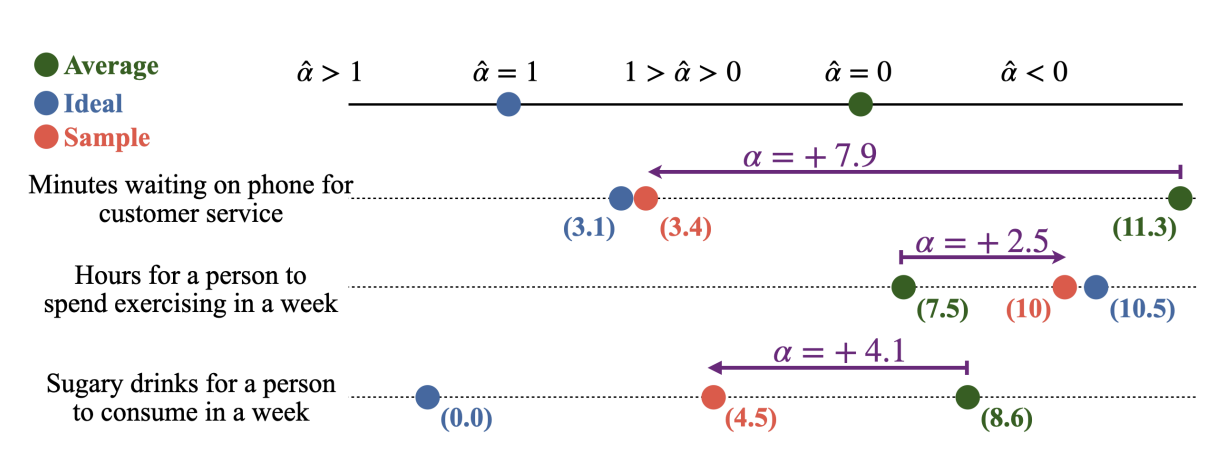
可以观察到：

• 客户服务等待时间：采样值比平均值显著偏小（$\alpha =+7.9$），说明模型倾向于低估等待时间，更接近理想化的“少等待”状态。
• 每周锻炼时间：采样值比平均值偏大（$\alpha =+2.5$），符合人类倾向于“多运动”的理想化认知。
• 含糖饮料摄入量：采样值显著低于平均值（$\alpha =+4.1$），反映出模型在健康相关任务中更接近“少喝”的理想化趋势。

这些实验结果验证了公式所描述的 统计分布 + 理想偏移 的采样机制，并揭示了 LLM 在多个现实领域中存在的系统性偏差。

4. 实验验证与结果分析（Experimental Validation and Results）

为了验证第 3 章提出的采样理论模型在实际语言生成中的适用性与稳健性，本章针对多个概念场景开展了系统实验，并结合定量统计与可视化分析，考察了 采样结果 $S(C)$ 与 统计均值 $A(C)$ 及 理想值 $I(C)$ 之间的关系。实验覆盖了不同分布形态与情感极性下的偏移特征，并比较了不同规模与训练方式的 LLM 在处方性成分上的差异。

---

4.1 采样结果与理想值的相关性

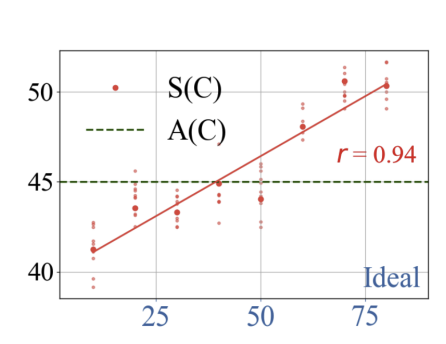
首先，我们在一组具有不同理想值的概念集合上，统计 LLM 的采样结果 $S(C)$ 与统计均值 $A(C)$ 的关系，并计算其与理想值 $I(C)$ 的相关性。如图 3 所示，红色散点表示不同概念的采样值 $S(C)$，绿色虚线表示统计均值 $A(C)$，横轴为理想值 $I(C)$。

可以看出，采样值与理想值之间呈现出高度正相关（皮尔逊相关系数 $r=0.94$），且大多数采样值明显偏离 $A(C)$，趋向于 $I(C)$ 所在的方向。这一结果与理论模型公式

$$S(C)=A(C)+\hat{\alpha }\cdot [I(C)-A(C)]$$

的预测一致，表明 $\hat{\alpha }$ 对采样偏移幅度具有显著的调节作用。

4.2 分布形态与情感极性的影响

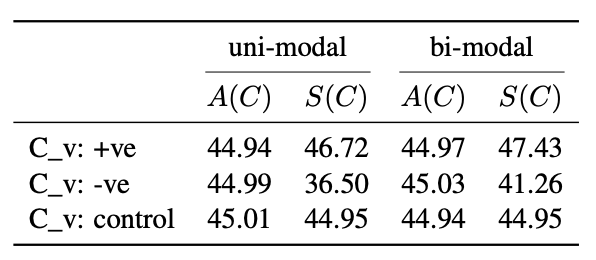
为了进一步分析偏移行为在不同分布形态与情感语境下的稳定性，我们分别构造了 单峰（uni-modal） 与 双峰（bi-modal） 分布条件，并在正向（+ve）、负向（-ve）和中性（control）三类概念上进行测试。表 1 给出了不同条件下的 $A(C)$ 与 $S(C)$ 对比结果。

结果表明，在正向情感概念中，采样值始终高于统计均值，说明模型倾向于放大正面特征；在负向情感概念中，采样值显著低于统计均值，显示出模型在面对负面情境时存在弱化趋势；而在中性概念中，二者几乎一致，表明偏移主要来源于理想值与均值之间的差异。此外，不同分布形态下的趋势高度一致，说明偏移效应具有较强的稳健性。

---

4.3 不同模型的处方性偏移比较

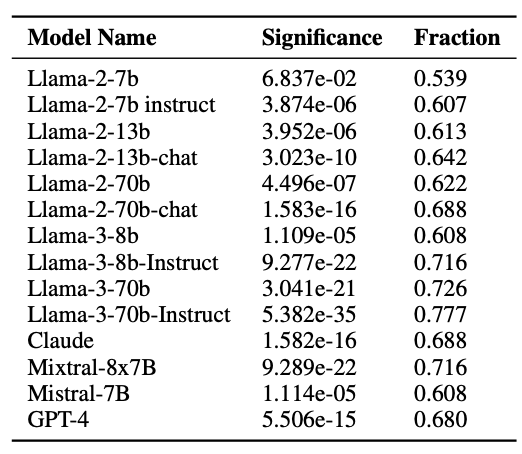
为了评估不同 LLM 的处方性成分差异，我们对包括 Llama 系列、Claude、Mistral、GPT-4 在内的多个模型进行了统计分析（见表 2）。表中 Fraction 表示在各领域中，采样值向理想值方向偏移的概念比例，Significance 表示该偏移的统计显著性。

结果表明：

1. 模型规模效应：较大规模的模型（如 Llama-3-70b、GPT-4）在 Fraction 指标上普遍更高，意味着更强的理想值驱动。
2. 训练方式效应：采用 RLHF（Reinforcement Learning from Human Feedback）训练的模型，其处方性偏移程度显著高于仅进行预训练的模型。
3. 跨模型一致性：无论架构与训练数据如何，几乎所有模型都表现出一致的向理想值偏移的趋势，验证了采样理论的普适性。

4.4 原型分数与理想值的关系（Prototype Scores and Their Relation to Ideal Values）

为了进一步探讨 处方性规范（Prescriptive Norms） 对大型语言模型（LLMs）生成行为的长期影响，本节引入 原型分数（Prototype Score，记作 $P(C)$）的分析。与单次采样结果 $S(C)$ 不同，$P(C)$ 来源于对概念 $C$ 的多个代表性实例（exemplars）进行独立评分后取均值，反映了模型在长期知识表征与中心倾向（central tendency）中的偏好。

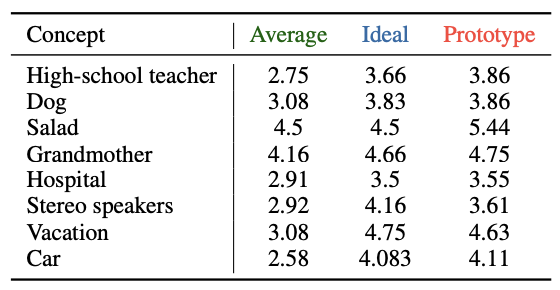
可以观察到，几乎所有概念的 $P(C)$ 都显著偏离 $A(C)$，并且这种偏移方向与 $I(C)$ 高度一致。例如：

• 在 High-school teacher、Dog、Salad、Grandmother 等概念中，$P(C)$ 明显高于 $A(C)$，且接近或超过 $I(C)$，表明模型在长期表征中更倾向于理想化描述；
• 对于 Hospital、Stereo speakers 等概念，虽然 $P(C)$ 与 $A(C)$ 的差距较小，但依然保持向 $I(C)$ 偏移的趋势；
• 在 Vacation 与 Car 等概念中，$P(C)$ 同样体现了与理想值一致的正向偏移。

这种趋势符合第 3 章提出的采样理论模型：

$$S(C)=A(C)+\hat{\alpha }\cdot [I(C)-A(C)]$$

其中，$P(C)$ 可以被视为多轮采样与知识固化作用下的稳定状态，即 $\hat{\alpha }$ 在长期迭代中的累积效果。这一结果表明，处方性偏移不仅在即时采样阶段存在，还会在模型的概念记忆与原型构建中被长期保留，从而影响后续生成。

---

4.5 小结（Summary）

综上，本章通过即时采样实验、分布与情感极性分析、跨模型比较以及原型分数研究，系统验证了 统计均值 + 理想值偏移 的采样理论模型，主要结论包括：

1. 即时偏移显著性：$S(C)$ 与 $I(C)$ 呈高度正相关，且显著偏离 $A(C)$，验证了理论公式的适用性；
2. 跨情境稳健性：无论分布形态（单峰、双峰）或情感极性（正向、负向、中性），偏移趋势保持一致；
3. 模型规模与训练方式影响：较大规模与采用 RLHF 训练的模型在处方性偏移比例上显著更高；
4. 长期效应存在性：$P(C)$ 的分析揭示了偏移在概念知识表征中的长期累积与固化。

这些发现表明，LLM 在生成过程中不仅遵循统计分布，还受到理想化规范的深刻影响，并且这种影响具有即时性与长期性双重特征。在未来应用中，应结合任务需求与公平性约束，对 $\hat{\alpha }$ 的作用范围和强度进行调节，以平衡生成结果的理想化与客观性。

➔➔➔➔点击查看原文，获取更多大模型相关资料

5. 总结与未来工作

本研究围绕大型语言模型（LLMs）在生成过程中的 采样机制，提出并验证了一个结合 统计均值 与 理想值偏移 的理论模型。通过系统化的实验设计，我们不仅揭示了 LLM 在即时生成阶段的处方性偏移行为，还进一步确认了该偏移在长期知识表征与原型构建过程中的固化趋势。

综合前文分析，可以得出以下核心结论：

1. 理论模型有效性：公式
   $$S(C)=A(C)+\hat{\alpha }\cdot [I(C)-A(C)]$$
   能够准确刻画 LLM 采样值 $S(C)$ 与统计均值 $A(C)$、理想值 $I(C)$ 之间的关系，且在多种概念、情感极性与分布形态下均表现出稳健性。
2. 偏移的普适性与一致性：无论模型架构、规模、训练方式如何，处方性偏移均为一致性趋势，表明这是 LLM 内部生成机制的共性特征。
3. 即时与长期双重影响：偏移不仅在单次采样中出现，还会在多轮采样和知识固化中累积形成稳定的原型分数 $P(C)$，长期影响模型输出。

该采样机制的发现，对于 模型可解释性（interpretability） 与 输出可控性（controllability） 研究具有重要意义：

• 在 健康、教育、公共沟通 等领域，合理的理想值偏移可以使输出更贴近人类社会的伦理与价值观；
• 在 政策决策、司法审判、风险评估 等高敏感度任务中，必须防范偏移带来的系统性误差，以确保公平性与客观性。

因此，$\hat{\alpha }$ 不仅是一个理论参数，也是未来调

➔➔➔➔点击查看原文，获取更多大模型相关资料