一、最大子数组和（LeetCode 53）

二、环形子数组的最大和（LeetCode 918）

三、乘积最大子数组（LeetCode 152）

四、乘积为正数的最长子数组长度（LeetCode 1567）

五、等差数列划分（LeetCode 413）

六、最长湍流子数组（LeetCode 978）

七、单词拆分（LeetCode 139）

八、环绕字符串中唯一的子字符串（LeetCode 467）

总结

动态规划（Dynamic Programming，简称 DP）是解决多阶段决策问题的有效方法，尤其在处理子数组、子串相关问题时，能通过状态定义和转移，高效找到最优解。下面结合几道经典题目，分享动态规划在这类问题中的分析方法与思路。

一、最大子数组和（LeetCode 53）

问题描述

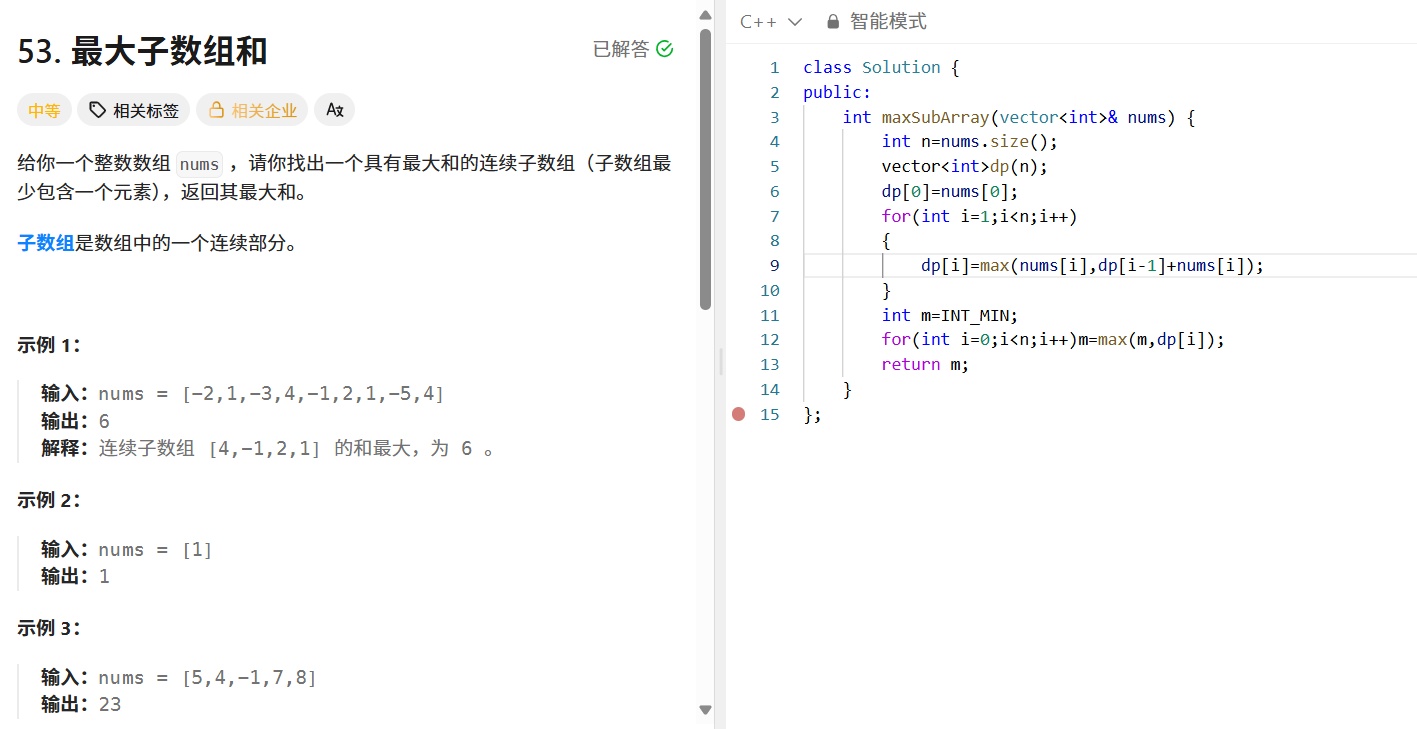
给定整数数组 nums ，找出和最大的连续子数组，返回其最大和。

分析思路

- 状态定义： dp[i] 表示以 nums[i] 结尾的连续子数组的最大和。
- 状态转移：对于 nums[i] ，有两种选择，要么加入前面的子数组（ dp[i - 1] + nums[i] ），要么自己作为新子数组的起点（ nums[i] ），取两者最大值，即 dp[i] = max(nums[i], dp[i - 1] + nums[i]) 。
- 初始条件： dp[0] = nums[0] ，因为第一个元素自己就是一个子数组。
- 结果提取：遍历 dp 数组，找到最大值。

代码实现

class Solution {
public:int maxSubArray(vector<int>& nums) {int n = nums.size();vector<int> dp(n);dp[0] = nums[0];for (int i = 1; i < n; i++) {dp[i] = max(nums[i], dp[i - 1] + nums[i]);}int maxSum = INT_MIN;for (int num : dp) {maxSum = max(maxSum, num);}return maxSum;}
};

二、环形子数组的最大和（LeetCode 918）

问题描述

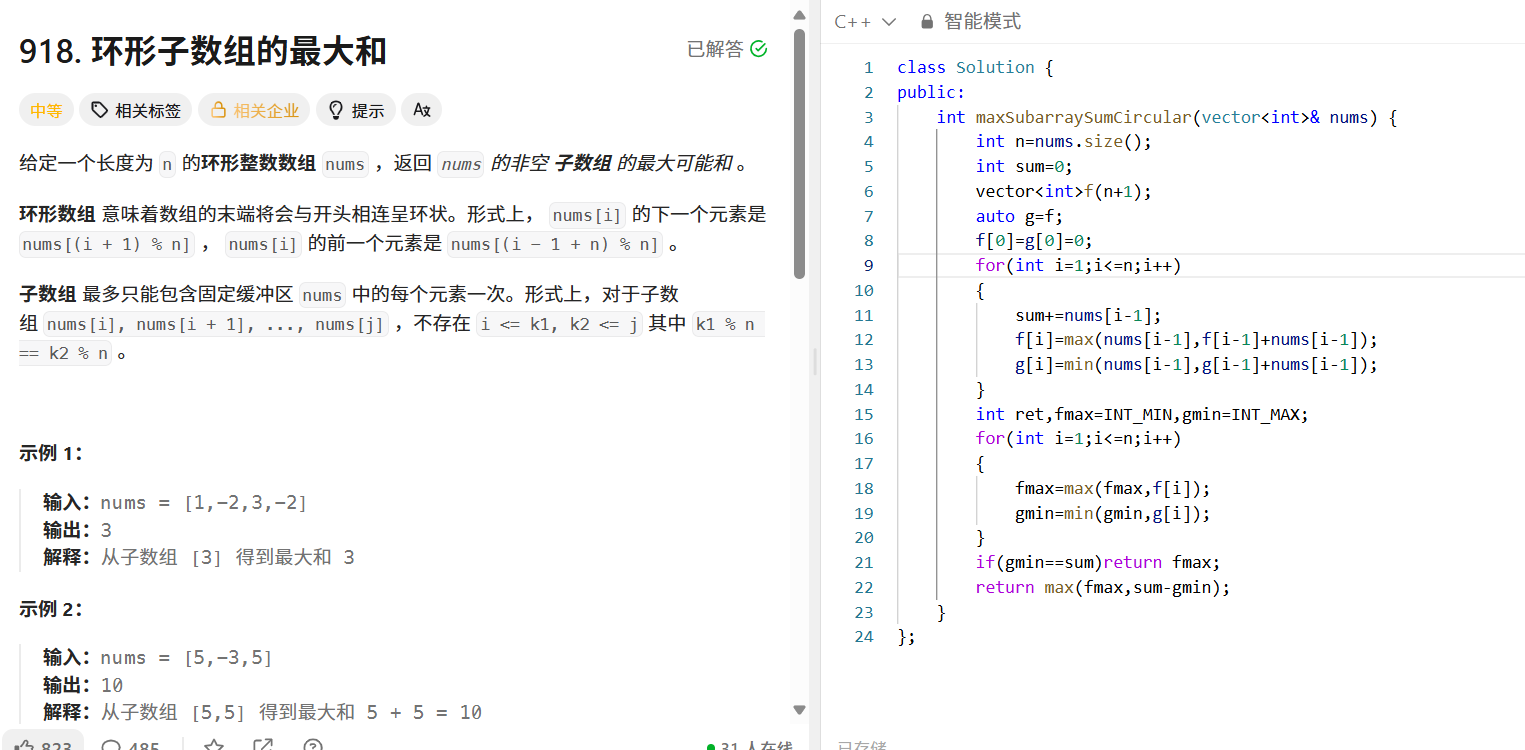
给定环形整数数组 nums ，返回非空子数组的最大可能和（环形意味着数组末端与开头相连）。

分析思路

环形子数组的最大和有两种情况：

- 情况一：最大和子数组在数组内部（非环形），可通过常规最大子数组和方法计算。
- 情况二：最大和子数组跨越数组首尾（环形），此时最大和等于数组总和减去内部最小子数组和。
需要注意，若数组所有元素都是负数，此时总和减去最小子数组和（也是负数）会得到错误结果，需单独判断。

代码实现

class Solution {
public:int maxSubarraySumCircular(vector<int>& nums) {int n = nums.size();int sum = 0;vector<int> f(n + 1);auto g = f;f[0] = g[0] = 0;for (int i = 1; i <= n; i++) {sum += nums[i - 1];f[i] = max(nums[i - 1], f[i - 1] + nums[i - 1]);g[i] = min(nums[i - 1], g[i - 1] + nums[i - 1]);}int fmax = INT_MIN, gmin = INT_MAX;for (int i = 1; i <= n; i++) {fmax = max(fmax, f[i]);gmin = min(gmin, g[i]);}if (gmin == sum) return fmax;return max(fmax, sum - gmin);}
};

三、乘积最大子数组（LeetCode 152）

问题描述

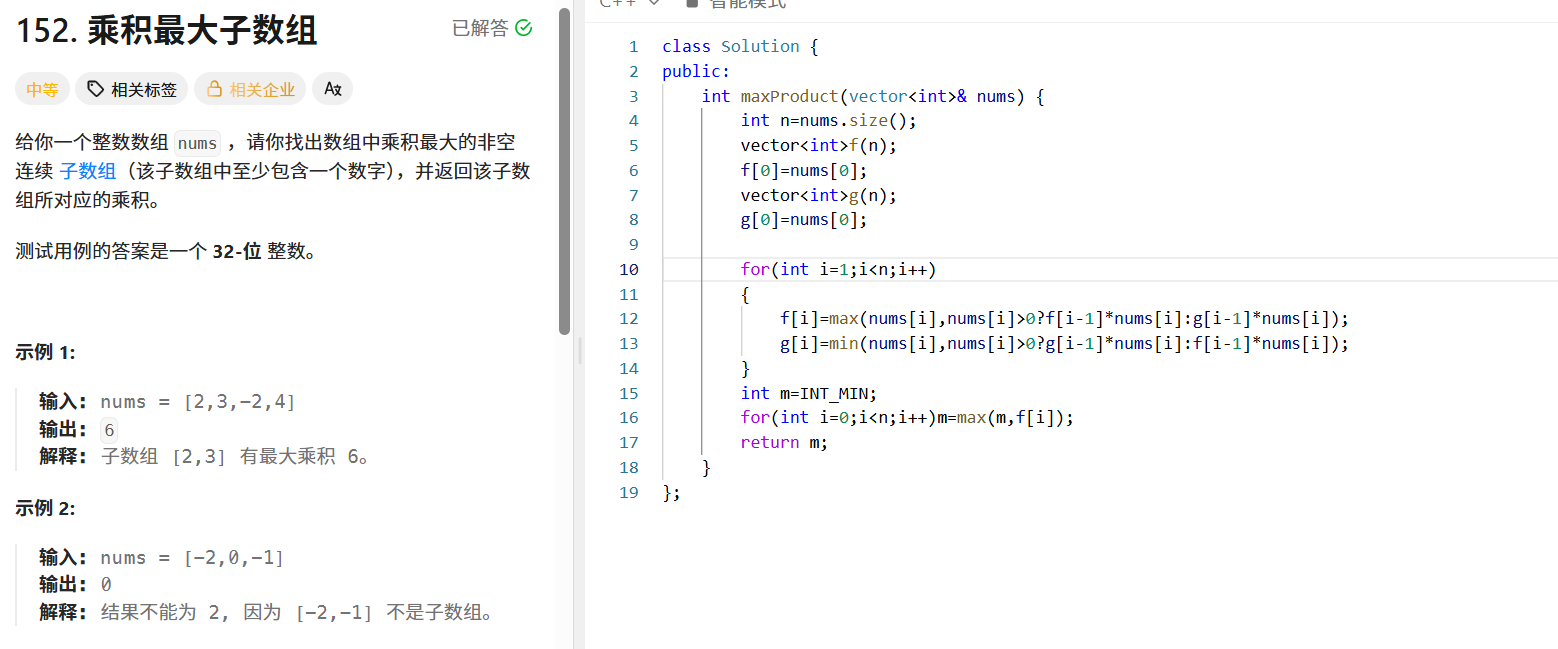
给定整数数组 nums ，找出乘积最大的非空连续子数组，返回该乘积。

分析思路

由于乘法的特殊性，负数相乘可能得到正数，所以需要同时记录以 nums[i]  结尾的子数组的最大乘积和最小乘积。

- 状态定义： f[i]  表示以 nums[i]  结尾的子数组的最大乘积， g[i]  表示以 nums[i]  结尾的子数组的最小乘积。
- 状态转移：根据 nums[i]  的正负，选择与 f[i - 1]  或 g[i - 1]  相乘，即：
- 若 nums[i] > 0 ， f[i] = max(nums[i], f[i - 1] * nums[i]) ， g[i] = min(nums[i], g[i - 1] * nums[i]) ；
- 若 nums[i] < 0 ， f[i] = max(nums[i], g[i - 1] * nums[i]) ， g[i] = min(nums[i], f[i - 1] * nums[i]) ；
- 若 nums[i] == 0 ， f[i] = g[i] = 0 。
- 初始条件： f[0] = g[0] = nums[0] 。
- 结果提取：遍历 f  数组，找到最大值。

代码实现

class Solution {
public:int maxProduct(vector<int>& nums) {int n = nums.size();vector<int> f(n);f[0] = nums[0];vector<int> g(n);g[0] = nums[0];for (int i = 1; i < n; i++) {if (nums[i] > 0) {f[i] = max(nums[i], f[i - 1] * nums[i]);g[i] = min(nums[i], g[i - 1] * nums[i]);} else if (nums[i] < 0) {f[i] = max(nums[i], g[i - 1] * nums[i]);g[i] = min(nums[i], f[i - 1] * nums[i]);} else {f[i] = g[i] = 0;}}int maxProd = INT_MIN;for (int num : f) {maxProd = max(maxProd, num);}return maxProd;}
};

四、乘积为正数的最长子数组长度（LeetCode 1567）

问题描述

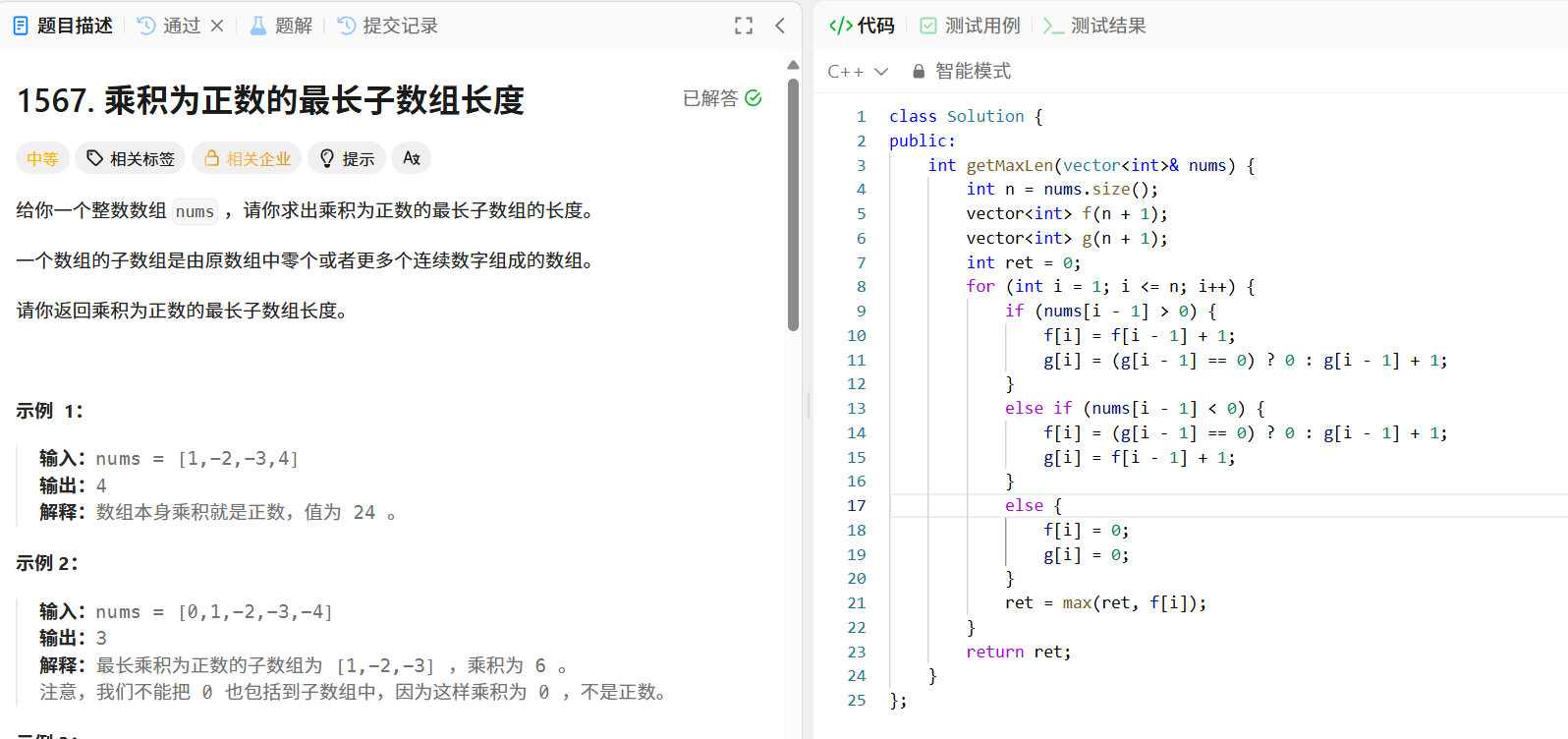
给定整数数组 nums ，求出乘积为正数的最长子数组的长度。

分析思路

- 状态定义： f[i]  表示以 nums[i - 1]  结尾的乘积为正数的最长子数组长度， g[i]  表示以 nums[i - 1]  结尾的乘积为负数的最长子数组长度。
- 状态转移：根据 nums[i - 1]  的正负进行转移：
- 若 nums[i - 1] > 0 ， f[i] = f[i - 1] + 1 ， g[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1 ；
- 若 nums[i - 1] < 0 ， f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1 ， g[i] = f[i - 1] + 1 ；
- 若 nums[i - 1] == 0 ， f[i] = g[i] = 0 。
- 初始条件： f[0] = g[0] = 0 。
- 结果提取：遍历过程中记录 f[i]  的最大值。

代码实现

class Solution {
public:int getMaxLen(vector<int>& nums) {int n = nums.size();vector<int> f(n + 1);vector<int> g(n + 1);int ret = 0;for (int i = 1; i <= n; i++) {if (nums[i - 1] > 0) {f[i] = f[i - 1] + 1;g[i] = (g[i - 1] == 0) ? 0 : g[i - 1] + 1;} else if (nums[i - 1] < 0) {f[i] = (g[i - 1] == 0) ? 0 : g[i - 1] + 1;g[i] = f[i - 1] + 1;} else {f[i] = 0;g[i] = 0;}ret = max(ret, f[i]);}return ret;}
};

五、等差数列划分（LeetCode 413）

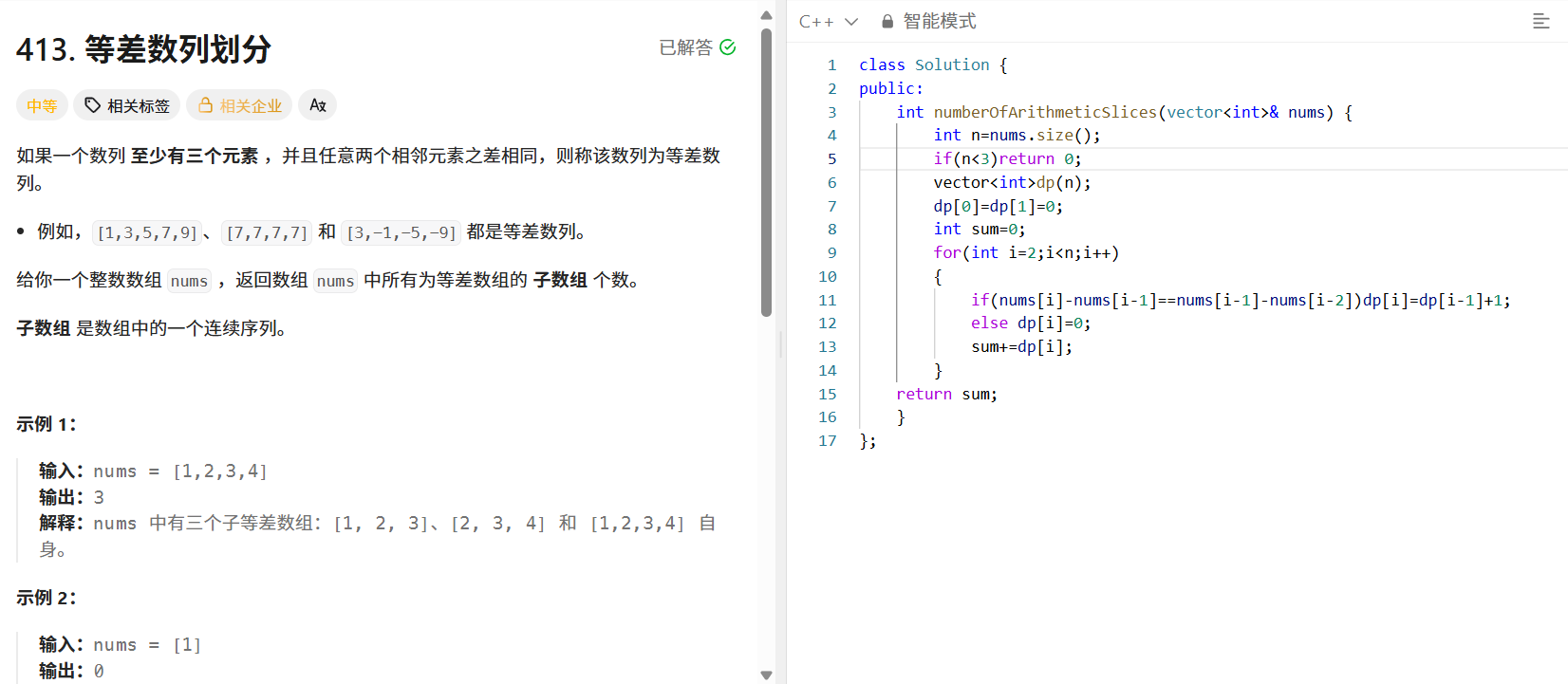
问题描述

如果一个数列至少有三个元素，且任意两个相邻元素之差相同，则称该数列为等差数列。给定整数数组 nums ，返回数组中所有为等差数组的子数组个数。

分析思路

- 状态定义： dp[i]  表示以 nums[i]  结尾的等差数列的个数。
- 状态转移：若 nums[i] - nums[i - 1] == nums[i - 1] - nums[i - 2] ，说明以 nums[i]  结尾能形成新的等差数列， dp[i] = dp[i - 1] + 1 ；否则 dp[i] = 0 。
- 初始条件： dp[0] = dp[1] = 0 ，因为前两个元素无法形成至少三个元素的等差数列。
- 结果提取：将所有 dp[i]  相加，得到总的等差数列子数组个数。

代码实现

  
class Solution {
public:int numberOfArithmeticSlices(vector<int>& nums) {int n = nums.size();if (n < 3) return 0;vector<int> dp(n);dp[0] = dp[1] = 0;int sum = 0;for (int i = 2; i < n; i++) {if (nums[i] - nums[i - 1] == nums[i - 1] - nums[i - 2]) {dp[i] = dp[i - 1] + 1;} else {dp[i] = 0;}sum += dp[i];}return sum;}
};

六、最长湍流子数组（LeetCode 978）

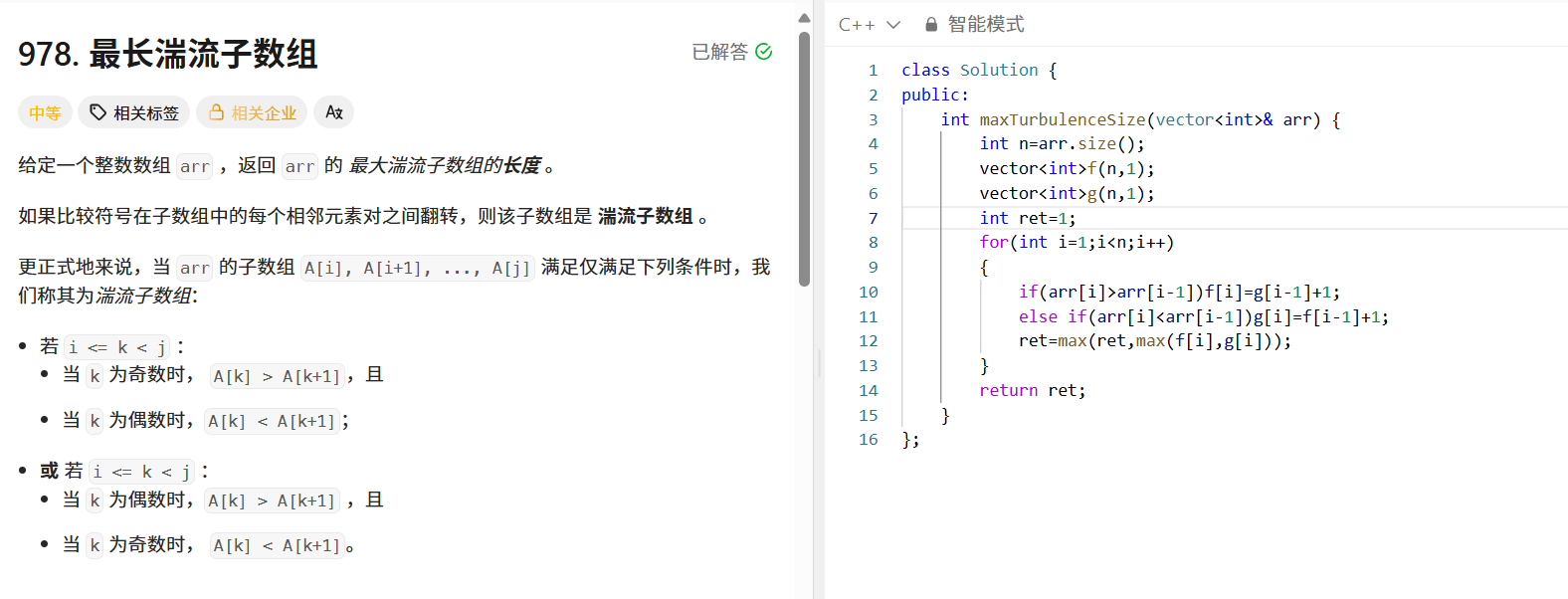
问题描述

给定整数数组 arr ，返回其最大湍流子数组的长度。湍流子数组是指相邻元素对之间比较符号翻转的子数组。

分析思路

- 状态定义： f[i] 表示以 arr[i] 结尾，且最后是上升（ arr[i] > arr[i - 1] ）的湍流子数组长度； g[i] 表示以 arr[i] 结尾，且最后是下降（ arr[i] < arr[i - 1] ）的湍流子数组长度。
- 状态转移：
- 若 arr[i] > arr[i - 1] ， f[i] = g[i - 1] + 1 ， g[i] = 1 ；
- 若 arr[i] < arr[i - 1] ， g[i] = f[i - 1] + 1 ， f[i] = 1 ；
- 若 arr[i] == arr[i - 1] ， f[i] = g[i] = 1 。
- 初始条件： f[0] = g[0] = 1 ，单个元素自身是长度为 1 的湍流子数组。
- 结果提取：遍历过程中记录 f[i] 和 g[i] 中的最大值。

代码实现

  
class Solution {
public:int maxTurbulenceSize(vector<int>& arr) {int n = arr.size();vector<int> f(n, 1);vector<int> g(n, 1);int ret = 1;for (int i = 1; i < n; i++) {if (arr[i] > arr[i - 1]) {f[i] = g[i - 1] + 1;g[i] = 1;} else if (arr[i] < arr[i - 1]) {g[i] = f[i - 1] + 1;f[i] = 1;} else {f[i] = g[i] = 1;}ret = max(ret, max(f[i], g[i]));}return ret;}
};

七、单词拆分（LeetCode 139）

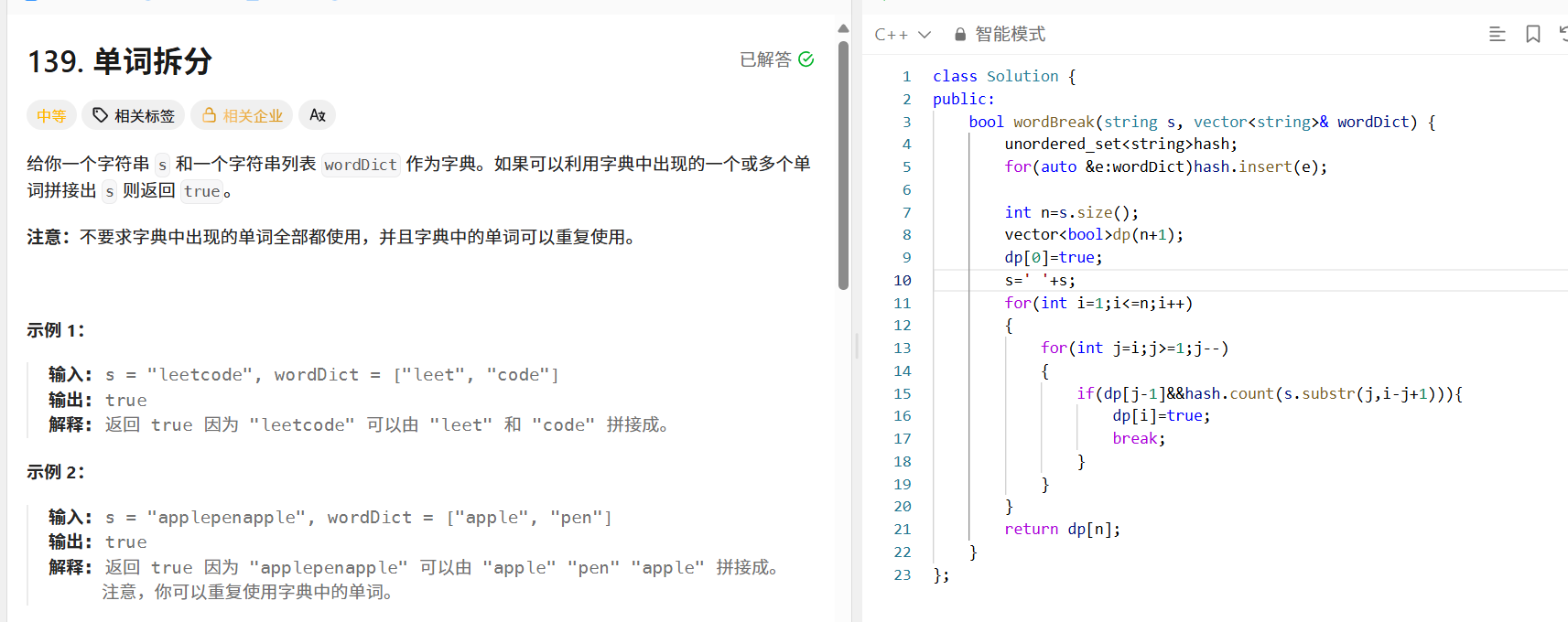
问题描述

给定字符串 s  和字符串列表 wordDict  作为字典，判断是否可以利用字典中出现的一个或多个单词拼接出 s 。

分析思路

- 状态定义： dp[i]  表示字符串 s  的前 i  个字符是否能被字典拼接而成。
- 状态转移：对于每个 i ，枚举分割点 j （从 i  到 1 ），若 dp[j - 1]  为 true （前 j - 1  个字符能被拼接）且 s  的 j  到 i  子串在字典中，则 dp[i] = true 。
- 初始条件： dp[0] = true ，空字符串能被拼接。
- 结果提取： dp[s.size()]  即为最终结果，表示整个字符串是否能被拼接。

代码实现

class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {unordered_set<string> hash;for (auto &e : wordDict) hash.insert(e);int n = s.size();vector<bool> dp(n + 1);dp[0] = true;s = " " + s;for (int i = 1; i <= n; i++) {for (int j = i; j >= 1; j--) {if (dp[j - 1] && hash.count(s.substr(j, i - j + 1))) {dp[i] = true;break;}}}return dp[n];}
};

八、环绕字符串中唯一的子字符串（LeetCode 467）

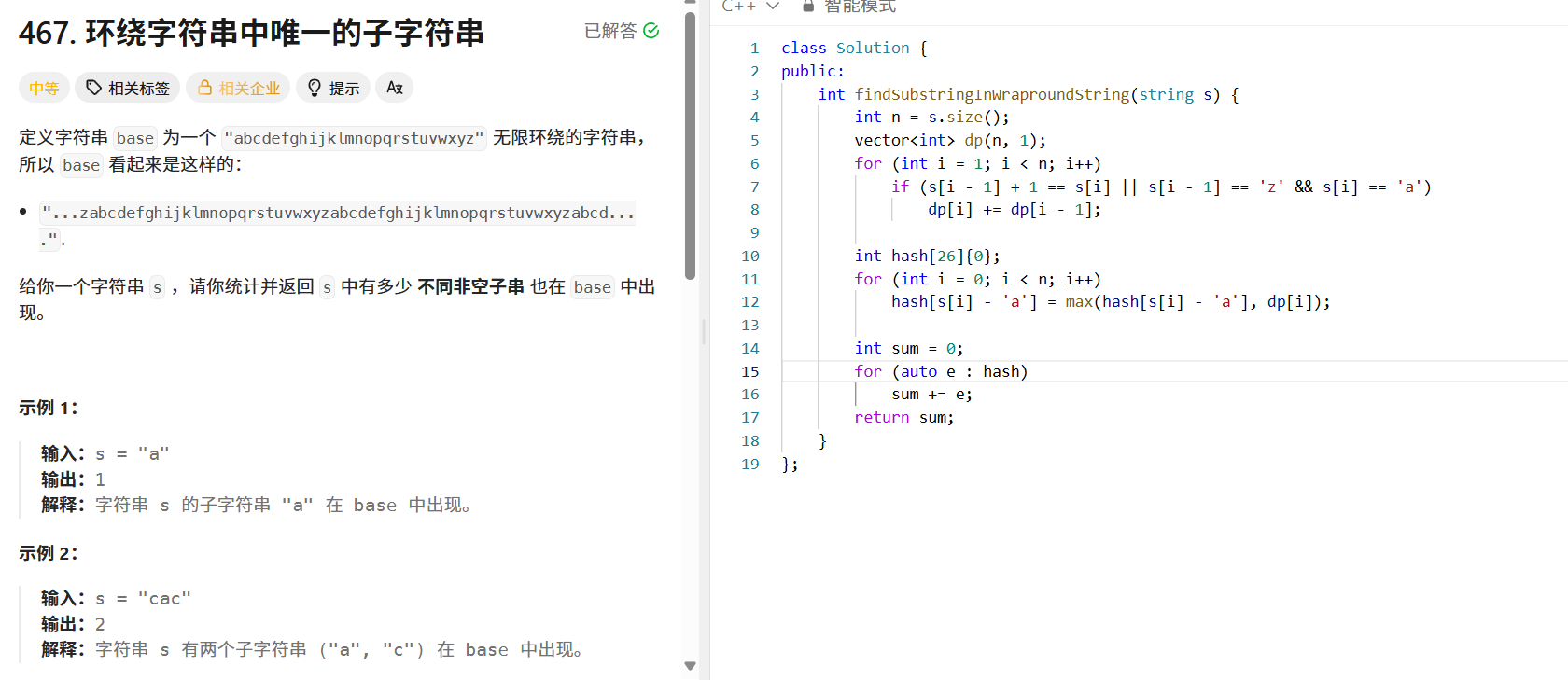
问题描述

定义字符串 base  为 "abcdefghijklmnopqrstuvwxyz"  无限环绕的字符串，给定字符串 s ，统计并返回 s  中有多少不同非空子串也在 base  中出现。

分析思路

- 状态定义： dp[i]  表示以 s[i]  结尾的符合 base  规律的子串长度。
- 状态转移：若 s[i - 1]  到 s[i]  符合 base  的连续规律（如 s[i - 1]  是 'z'  且 s[i]  是 'a' ，或 s[i] = s[i - 1] + 1 ），则 dp[i] = dp[i - 1] + 1 ；否则 dp[i] = 1 。
- 去重处理：用长度为 26 的数组 hash  记录每个字符结尾的最长符合规律子串长度，最后将所有 hash  元素相加，得到不同子串的个数（因为最长长度包含了所有更短的以该字符结尾的符合规律子串）。

代码实现

class Solution {
public:int findSubstringInWraproundString(string s) {int n = s.size();vector<int> dp(n, 1);for (int i = 1; i < n; i++) {if (s[i - 1] + 1 == s[i] || (s[i - 1] == 'z' && s[i] == 'a')) {dp[i] += dp[i - 1];}}int hash[26] = {0};for (int i = 0; i < n; i++) {hash[s[i] - 'a'] = max(hash[s[i] - 'a'], dp[i]);}int sum = 0;for (auto e : hash) {sum += e;}return sum;}
};