当磁化自旋系统被射频脉冲扰动而偏离其热平衡态后,一旦移除外部激励并给予足够时间,系统将根据热力学定律返回平衡态。这一过程包含三个特征现象:
(a) 自由进动——宏观磁化矢量 (M⃗\vec{M}M) 绕( B0⃗\vec {B_0}B0 )场的进动;
(b) 纵向弛豫——纵向磁化分量(Mz{M_z}Mz) 的恢复;
© 横向弛豫——横向磁化分量 (Mxy{M_{xy}}Mxy) 的衰减。
弛豫过程源于原子核周围由随机热运动产生的时变微观磁场,但具体机制因自旋系统而异,过于复杂。实际上不管是激发还是弛豫,只有量子力学才能完全精确的给出数学解释,此处仅通过布洛赫方程进行唯象描述,它提供足够的精度,对MR成像而言也足够了
忽略射频激励项后,在拉莫尔旋转坐标系中,弛豫过程由以下方程描述:
{dMz′dt=−Mz′−Mz0T1dMx′y′dt=−Mx′y′T2(3.121)
\left\{
\begin{array}{l}
\frac{d M_{z'}}{d t} = -\frac{M_{z'} - M_z^0}{T_1} \\
\frac{d M_{x'y'}}{d t} = -\frac{M_{x'y'}}{T_2}
\end{array}
\right. \tag {3.121}
{dtdMz′=−T1Mz′−Mz0dtdMx′y′=−T2Mx′y′(3.121)
其中 Mz0M_z^0Mz0 为热平衡态纵向磁化强度,T1T_1T1 和 T2T_2T2 分别为描述纵向和横向弛豫过程的时间常数。解方程 (3.121) 得:
{Mx′y′(t)=Mx′y′(0+)e−t/T2Mz′(t)=Mz0(1−e−t/T1)+Mz′(0+)e−t/T1(3.122)
\left\{
\begin{array}{l}
M_{x'y'}(t) = M_{x'y'}(0_+) e^{-t/T_2} \\
M_{z'}(t) = M_z^0 (1 - e^{-t/T_1}) + M_{z'}(0_+) e^{-t/T_1}
\end{array}
\right. \tag {3.122}
{Mx′y′(t)=Mx′y′(0+)e−t/T2Mz′(t)=Mz0(1−e−t/T1)+Mz′(0+)e−t/T1(3.122)
此处 Mx′y′(0+)M_{x'y'}(0_+)Mx′y′(0+) 和 Mz′(0+)M_{z'}(0_+)Mz′(0+) 分别表示射频脉冲结束后,旋转坐标系下观测到的初始横向和纵向磁化分量。
值得注意的是,T1T_1T1 和 T2T_2T2 并不是纵向和横向弛豫的完成时间。为了说得更加清楚,假设热平衡态下产生一个 x′x'x′ 轴90度射频脉冲,在射频脉冲激发前(t=0−)(t=0_{-})(t=0−)和射频脉冲激发后(t=0+)(t=0_{+})(t=0+)的横向和纵向磁化分量如下所示:
{Mxy′(0−)=0Mz′(0−)=Mz0→90x′{Mxy′(0+)=Mz0Mz′(0+)=0
\begin{cases}
M_{xy^{\prime}}(0_{-}) = 0 \\
M_{z^{\prime}}(0_{-}) = M_{z}^{0}
\end{cases}
\xrightarrow{90_{x^{\prime}}}
\begin{cases}
M_{xy^{\prime}}(0_{+}) = M_{z}^{0} \\
M_{z^{\prime}}(0_{+}) = 0
\end{cases}
{Mxy′(0−)=0Mz′(0−)=Mz090x′{Mxy′(0+)=Mz0Mz′(0+)=0
而在 t>0t>0t>0 的时的横向和纵向磁化分量如下所示:
{Mx′y′(t)=Mz0e−t/T2Mz′(t)=Mz0(1−e−t/T1)
\left\{
\begin{array}{l}
M_{x'y'}(t) = M_{z}^{0} e^{-t/T_2} \\
M_{z'}(t) = M_z^0 (1 - e^{-t/T_1})
\end{array}
\right.
{Mx′y′(t)=Mz0e−t/T2Mz′(t)=Mz0(1−e−t/T1)
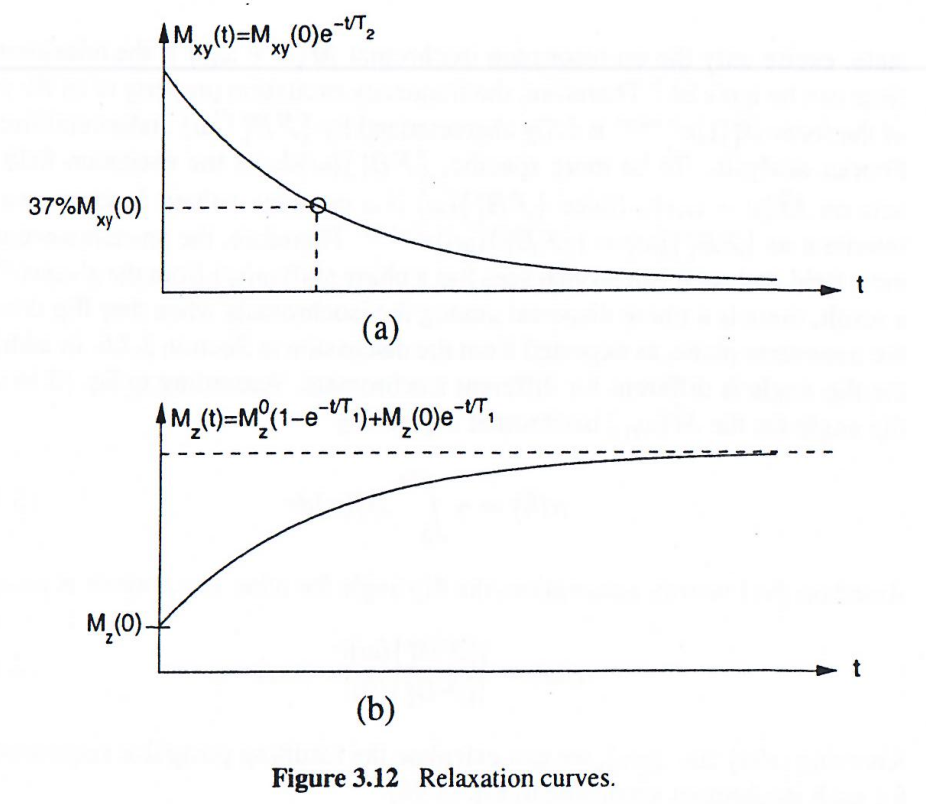
然后定义,当横向磁化分量衰减为初始值Mx′y′(0+)M_{x'y'}(0_+)Mx′y′(0+)的37%的时刻就是 T2T_2T2 ,而当纵向磁化分量恢复为热平衡态时的63%的时刻就是 T1T_1T1: {Mx′y′(T2)≈37%Mx′y′(0+)Mz′(T1)≈63%Mz0\left\{\begin{array}{l}M_{x'y'}(T_2) \approx 37\% M_{x'y'}(0_+)\\M_{z'}(T_1) \approx 63\% M_z^0 \end{array}\right.{Mx′y′(T2)≈37%Mx′y′(0+)Mz′(T1)≈63%Mz0
生物组织典型值:
- T1T_1T1范围:300–2000 ms
- T2T_2T2范围:30–150 ms
- 对一个给定的自旋系统, T1T_1T1 > T2T_2T2
应用 (3.64)到(3.122) ,将旋转坐标系下磁化矢量转换到实验室坐标系:
Mxy(t)=Mxy(0+)e−t/T2e−iω0tMz(t)=Mz0(1−e−t/T1)+Mz(0+)e−t/T1
\begin{align*}
M_{xy}(t) &= M_{xy}(0_+) e^{-t/T_2} e^{-i\omega_0 t} \tag {3.124a} \\
M_z(t) &= M_z^0 (1 - e^{-t/T_1}) + M_z(0_+) e^{-t/T_1} \tag {3.124b}
\end{align*}
Mxy(t)Mz(t)=Mxy(0+)e−t/T2e−iω0t=Mz0(1−e−t/T1)+Mz(0+)e−t/T1(3.124a)(3.124b)
其中
Mxy(0+)=Mx′y′(0+)e−iω0τp(3.125)M_{xy}(0_+) = M_{x'y'}(0_+) e^{-i\omega_0 \tau_p} \tag {3.125}Mxy(0+)=Mx′y′(0+)e−iω0τp(3.125)
式(3.125)这是在实验室坐标系中由信号检测系统观测到的“初始”横向磁化分量的强度。包含时间延迟项是因为我们在脉冲结束时(t=τpt=\tau_pt=τp,其中τp\tau_pτp为脉冲持续时间)将时间重置为零,以便描述弛豫效应。
式(3.124)给出了射频脉冲后横向与纵向磁化强度随时间演化的"精确"唯象描述。具体而言,从方程(3.124a)可明确看出:在实验室坐标系中,横向磁化强度的演化特征表现为指数衰减e−t/T2e^{-t/T_{2}}e−t/T2和绕B0B_{0}B0场的进动e−iw0te^{-iw_{0}t}e−iw0t。自由进动周期的时长取决于T2T_{2}T2值。对于生物组织而言,T2T_{2}T2值通常在数十毫秒量级,这使得在此期间能够检测到磁共振信号。
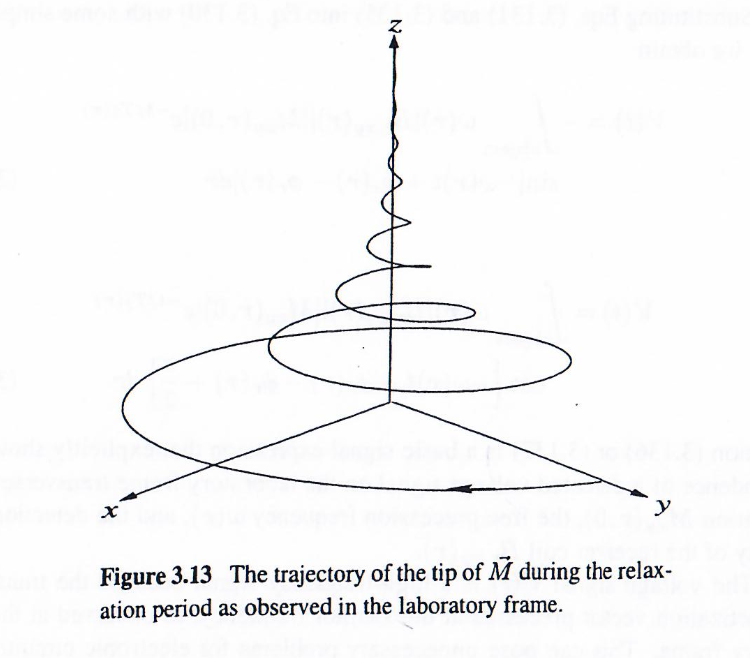
需要特别说明的是,当M⃗\vec{M}M因弛豫过程以螺旋运动方式”回归“z轴时(如上图所示),其模长并不守恒。该行为与激发期间M⃗\vec{M}M保持固定模长从z轴螺旋下行的运动特性存在本质区别。简单的说,是因为:
- 射频激发存在聚相的作用,这使得 z′z'z′ 轴宏观磁化强分量 Mz′M_{z'}Mz′ “全都”转换为 x′y′x'y'x′y′ 平面宏观磁化强分量 Mx′y′M_{x'y'}Mx′y′
- 弛豫过程中,聚相效果消失,因为失相,导致 x′y′x'y'x′y′ 平面宏观磁化强分量 Mx′y′M_{x'y'}Mx′y′ 快速衰减(相互抵消),但是这部分抵消并不能转化为 z′z'z′ 轴的宏观磁化强分量 Mz′M_{z'}Mz′,
- Mz′M_{z'}Mz′ 方向的恢复,实际上是高能级的原子跃迁回落到低能级
失相的唯象解释(不是精确的量子力学角度的解释):
- 不同原子所处微观磁场环境不同,使得不同的原子的进动频率略有不同
- 这使得原本相位同步的进动,开始慢慢分离,最后相互抵消,失相的过程请看下图
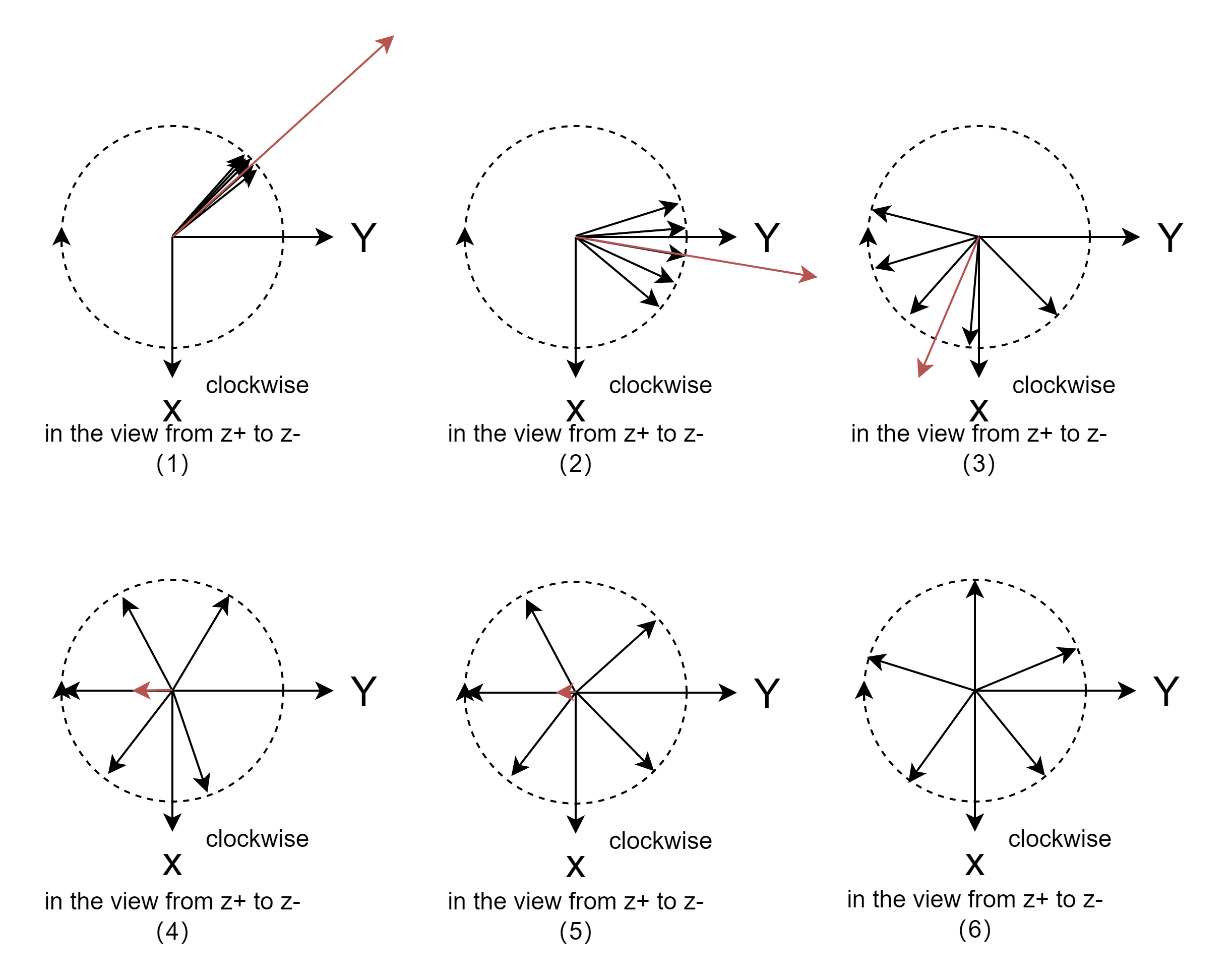
- 下图是实验室坐标下的 xyxyxy 平面,不同原子的磁矩 u⃗n\vec u_nun的 xyxyxy 分量uxy,nu_{xy,n}uxy,n (下图黑线)和净宏观磁化矢量分量 MxyM_{xy}Mxy (下图红线)
- 下图1,射频激发刚结束,不同原子的磁矩 u⃗n\vec u_nun 的 xyxyxy 分量uxy,nu_{xy,n}uxy,n 仍保持同相,其合成后的净宏观磁化矢量分量 MxyM_{xy}Mxy 处于最大值,为Mxy(0+)M_{xy}(0_+)Mxy(0+)
- 下图2,不同原子的磁矩 u⃗n\vec u_nun 的 xyxyxy 分量uxy,nu_{xy,n}uxy,n 因为进动频率不同,在相同时间的旋转角度不同,致使逐渐失去同相,他们的叠加后的MxyM_{xy}Mxy 开始衰减
- 下图3,4,5,是一个失相逐渐扩大的横向弛豫过程
- 下图6,弛豫完成,叠加后的净宏观磁化矢量分量MxyM_{xy}Mxy 为0





,并在同一窗口显示)











并测试脚本执行情况)

