我们清楚的知道法拉第圆盘发电机的原理。当导线切割磁感线的时候，会产生电流，当然电流产生需要的是电动势，也就是，

这里写不写，避免和电场强度混淆。根据上面的分析，我们知道磁场强度特斯拉的单位，用时间单位制表示的话就是秒的平方或者赫兹的平方，假定它是赫兹的平方，也就是秒的平方的倒数，而加速度的单位是米每二次方秒，也就是说，

将单位变换换回对应的物理量，

对比，

可见，

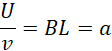
也就是说，如果切割磁感线，就会产生电势差，那么不切割磁感线，就会产生加速度。具体来说，就是对电荷产生加速度。而这个加速度表现为电势差和运动速度的比值。可是既然不切割磁感线，哪有运动速度？其实这并不矛盾，因为并没有真正意义上的静止，甚至是相对静止。我们在考虑运动速度的时候，说的是相对运动，也包括相对静止，

实际上应当写成，

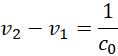
也就是光速的倒数，因为光速和宏观虚数单位，成正比，

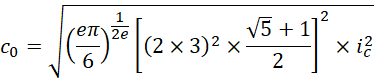
根据虚数单位的可伸缩性，它可以被认为就是宏观虚数单位本身。那么这样的话，

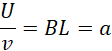
当，

可得，

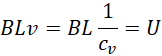
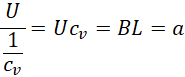
其中相对速度可以直接用绝对速度代替，是因为旋转的参照系为旋转中心，旋转中心在旋转过程中应当被认为是绝对静止的。事实上当然不是，但是它既然和成比例关系，也就可以被认为是相对数值上的相对数值即可。这样的话，就得到了，

需要强调的是，虽然写成，并不是把磁体放在金属圆盘上就可以了，旋转仍然是必要的，只是此时圆盘径向上的等效金属导线并不“切割”磁感线。因为无论如何，必然存在，所以也一定存在。也就是说，这个磁体和圆盘一同旋转的系统，仍然可以产生中心和边缘上的电势差，如果连接中心和边缘构成回路，它仍然可以发电。只是这个数值非常大，对应的就非常小。

那么这种发电方式和常规的法拉第圆盘发电机的发电方式到底有何区别？区别就在于是否“切割”磁感线，也就是说，电流或者电子的有序运动是否和磁感线出现相对运动。或者说，相对运动的磁场和相对静止的磁场并不相同。

再观察，

若确定和在给定转速的前提下会产生确定的，虽然它的数值非常小。但如果给出用电器，或者给出另外的电动势，并确定和转速，那么我们就可以调制出需要的，也就是调制出特定的。如果给出用电器R，则会导致下降提升。但需要意识到的是，这个提升是相对于转动中心静止的效果，也就是说，完全可能是转动中心的频率下降导致的相对提升，因为从能量守恒定律的角度来说，用电器R导致电能转化为热能，系统整体的能量是降低的。那么其中频率提升的部分效果，实际上是整体能量降低的结果。

磁体和圆盘相对静止，一起绕着中心转动，满足这个条件，我们只需要购买一块中心有孔表面有金属镀层的钕铁硼磁体（一般铁氧体磁体表面没有金属镀层），将中心的孔穿在电机轴上，由电机驱动其转动。由于L就是半径，在磁体的标号确定的前提下，半径越大，的可调范围越大，可实验的范围越大，对转速的要求就越低。

下一个问题就是电势差，我们知道这个电势差可以由转动产生，但是也可以由外加的电动势产生。事实上如果可以积累电荷，则这个电势差也可以不断增大或者反向增大。但是若要保持电势差的积累，就需要某种单向导电性的材料，比如半导体材料。允许电荷从一端走向另一端却不允许其返回。另外就是必须实现电容的效果。当然一块有金属镀层的钕铁硼磁体并不满足这个要求。满足这些要求的可能就是SEG了，反过来说，按照这些要求去实作，我们就可以获得一个SEG设备。

从设备的结构不难看出，向着不同方向旋转，结果是不同的。按照右手定则，一个方向旋转产生的是内正外负的电势差，另一个方向旋转产生的是内负外正的电势差。由于电子自身存在内在的电势差，两个旋向产生的效果也是不对称的。对于，

来说，当等效电容造成的“外部”电势差占据主导，就可以被调制为某种特定的数值。而根据，

若电势差数值足够大或者足够小，则系统就可以对外体现出特定的加速度，也就是引力或者斥力的效应。这种现象也在约翰瑟尔的SEG以及俄罗斯复制的SEG实验中获得了验证（体现为漂浮或者减重效应）。

回到光速，我们知道光速和宏观虚数单位成正比，也就是说，实际上要当作虚数单位用的光速，不是299792458米每秒，而是某个速度的一千万倍。

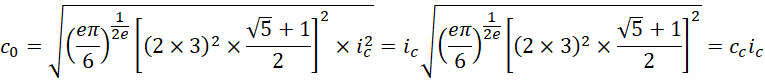
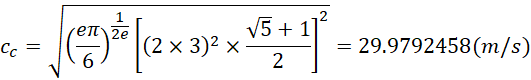
这个就是这个虚数系统和单位1之间的偏移量。也就是说，这个将近30米每秒的速度，就是这个系统的单位1，而以它为单位1的虚数单位的数值就是299792458米每秒，以它为单位1的无限，也就是-1的大小就是，以它为单位1的虚数单位的倒数就是

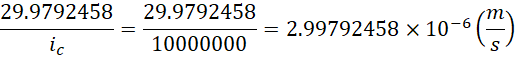
也就是3微米每秒。所以真实的最小速度的最大值就是3微米每秒，也就是。

中的，

已知N52磁体的剩磁强度为1.42T-1.48T，假定为1.45T，圆盘半径为5cm，也就是，

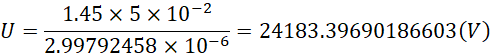
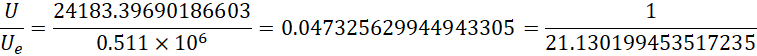
这个电压约为电子内在电压的二十一分之一。所以如果选择半径为1米的圆盘，

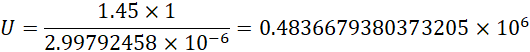
几乎就可以达到一个电子的内在压差，或者说使得一个电子跳出来。这里显然都没有涉及圆盘的旋转速度，但是我们知道，磁场方向，运动方向以及电势差的方向三种必须互相垂直，所以必须有一个旋转的速度以保证方向的垂直，但是具体转速的大小在这里并未体现。但如果边缘线速度小于30米每秒（也就是29.9792458米每秒），的数值就会更小，由此可以假定线性关系，速度总是单位速度的整数倍，

对于边缘线速度为，半径为的圆盘，

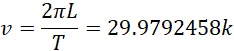
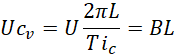
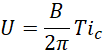
对于上面提到的标号为N52的钕铁硼磁体，若要在边缘产生一个电子的内在频差，进而得到一个电子，需要，

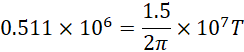
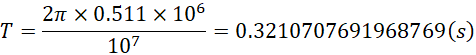
转动周期似乎是和半径无关的。但到底是不是这样，让我们看具体例子。

假定具有金属镀层的钕铁硼磁体半径是5cm，带动其转动的电机使其达到转速10000转每分钟，也就是167转每秒，则转动周期为，此时边缘线速度为，

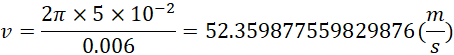
对比，

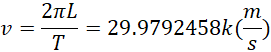
可见两者具有接近2倍的关系。于是可以选择，

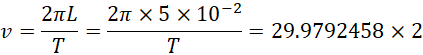
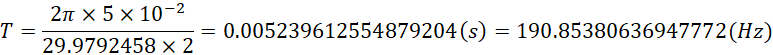
也就是转每秒，也就是转每分钟。在这个速度上就可能从圆盘边缘产生电子。如果选择，

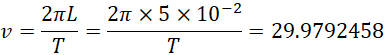
也就是大约5726转每分钟的时候也可以在边缘产生电子。随着转速的增加，整数k逐渐增大，单位时间里面，边缘可以产生的电子逐渐增多。由于存在量子效应，产生电子的速度是不连续的。

回顾俄罗斯SEG实验的设备，滚轮定子直径为1米（半径0.5米），滚轮支架直径为1.2米（半径0.6米），滚轮直径10厘米（半径0.05米），定子剩磁为1T，滚轮剩磁为1.2T，在550转每分钟（9.16转每秒）到600转每分钟（10转每秒，0.1秒每转）之间出现明显的实验效果，滚轮的转速，

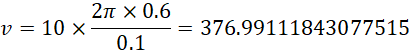
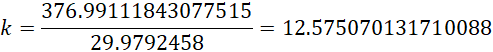
也就是大约12倍，而这正是滚轮的个数。由于滚轮和定子之间存在空气间隙，也就构成电容，进而就可以产生外加电场，从而改变设备的，进而导致其它实验现象的产生。

回到我们自己的实验，我们的设备只有10厘米的直径，转速需要达到5726转才能获得电子，这个数值当然也可以实现。下一步我们需要的是在圆盘周围加上一层半导体层，半导体层之外再加上一层金属层，这就构成了电容结构。电荷单向移动使得电容充电，这就建立了外电场，外电场和内电场之间的交互作用，就可以有效的改变设备的的数值，进而实现本地时空的绝对速度改变的要求。