
1、 机器学习中特征的理解
def: 特征选择和降维
特征选择:原有特征选择出子集 ,不改变原来的特征空间
降维:将原有的特征重组成为包含信息更多的特征, 改变了原有的特征空间降维的主要方法
Principal Component Analysis (主成分分析)
Singular Value Decomposition (奇异值分解)
特征选择的方法
Filter 方法 :卡方检验、信息增益、相关系数
Wrapper 方法 :其主要思想是:将子集的选择看作是一个搜索寻优问题 ,生成不同的组合 ,对组合进行评价 ,再与其他的组合进行比较。这样就将子集的选择看作是一个是一个优化问题 ,这里有很多的优化算法可以解决 ,尤其是一些启发式的优化算法 ,如 GA, PSO, DE ,ABC 等 ,详见“优化算法 —— 人工蜂群算法 (ABC)”,“优化算法 —— 粒子群算法 (PSO)”。
Embedded 方法 :其主要思想是 :在模型既定的情况下学习出对提高模型准确性最好的属性。这句话并不是很好理解 ,其实是讲在确定模型的过程中 ,挑选出那些对模型的训练有重要意义的属性。
主要方法 :正则化。 岭回归就是在基本线性回归的过程中加入了正则项。
2、机器学习中 ,有哪些特征工程方法?
数据和特征决定了机器学习的上限, 而 模型和算法只是逼近这个上限而 已
(1)计算每— 个特征与相应变量的相关性: 工 程上常用 的手 段有计算皮 尔逊系数和互信息系数, 皮 尔逊系数只能衡量线性相关性而 互信息系数能够很好地度量各种相关性,但是计算相对复杂— 些,好在很多toolkit里 边都包含了这个工 具(如 sklearn的MINE) ,得到相关性之后就可以排序选择特征了;
(2)构建单个特征的模型 ,通过模型的准确性为特征排序 ,借此来选择特征;
(3)通过L1正则项来选择特征: L1正则方 法具有稀疏解的特性, 因此天然具备特征选择的特性 ,但是要注意,L1没有选到的特征不代表不重要,原因是两个具有高 相关性的特征可能只保留了— 个,如果要确定哪个特征重要应再通过L2正则方 法交叉检验*;
(4)训练能够对特征打分的预选模型:RandomForest和Logistic Regression等都能对模型的特征打分,通过打分获得相关性后再训练最终模型;
(5)通过特征组合后再来选择特征 :如对用 户id和用 户特征最组合来获得较大 的特征集再来选择特征 ,这种做法在推荐系统和广 告系统中比 较常见 ,这也是所谓亿级甚至 十 亿级特征的主要来源 ,原因是用 户数据比 较稀疏 ,组合特征能够同时兼顾全局模型和个性化模型 ,这个问题有机会可以展开讲。
(6)通过深度学习来进行 特征选择: 目 前这种手 段正在随着深度学习的流行而 成为— 种手 段 ,尤其是在计算机视觉领域 ,原因是深度学习具有自 动学习特征的能力 ,这也是深度学习又 叫unsupervised feature
learning的原因。从深度学习模型中选择某— 神经层的特征后就可以用 来进行 最终目 标模型的训练了。
3、机器学习中的正负样本
在分类问题中 ,这个问题相对好理解— 点, 比 如人 脸识别中的例子 ,正样本很好理解 ,就是人 脸的图片 ,
负样本的选取就与问题场景相关 ,具体而 言 ,如果你要进行 教室中学生 的人 脸识别 ,那么负样本就是教室的窗子 、墙等等 ,也就是 说 ,不能是与你要研究的问题毫不相关的乱七八 糟的场景图片 ,这样的负样本并没有意义。负样本可以根据背景生 成,
有时候不需要寻找额外的负样本。— 般3000-10000的正样本需要5,000,000-100,000,000的负样本来学习,在互金 领域— 般在入 模前将正负比 例通过采样的方 法调整到3)1-5:1。
区别:所谓线性分类器即用 — 个超平面 将正负样本分离开 ,表达式为 y =wx 。这里 强调的是平面 。
而非 线性的分类界面 没有这个限制,可以是曲面 ,多个超平面 的组合等。典型的线性分类器有感知机,LDA,逻辑斯特回归, SVM(线性核);
典型的非 线性分类器有朴素贝 叶斯(有文 章说这个本质是线性的,http://dataunion.org/12344.html),kNN,决策树, SVM( 非 线性核)
优缺点: 1.线性分类器判别简单、易实现、且需要的计算量和存储量小 。
为解决比 较复杂的线性不可分样本分类问题 ,提出非 线性判别函数。超曲面 , 非线性判别函数计算复杂,
实际应用 上受到较大 的限制。在线性分类器的基础上, 用 分段线性分类器可以实现复杂的分类面 。解决问题比 较简便的方 法是采用 多个线性分界面 将它们分段连接, 用 分段线性判别划分去逼近分界的超曲面 。
如果— 个问题是非 线性问题并且它的类边界不能够用 线性超平面 估计得很好 ,那么非 线性分类器通常会比线性分类器表现得更精准。如果— 个问题是线性的 ,那么最好使用 简单的线性分类器来处理。
5、如何解决过拟合问题
解释过拟合:
模型在训练集表现好 ,在真实数据表现不好, 即模型的泛化能力 不够。从另外— 个方 面 来讲,模型在达到经验损失最小 的时候 ,模型复杂度较高 ,结构风 险没有达到最优。
解决:
学习方 法上: 限制机器的学习 ,使机器学习特征时学得不那么彻底, 因此这样就可以降低机器学到局部特征和错误特征的几 率 ,使得识别正确率得到优化.
数据上 :要防止 过拟合 ,做好特征的选取。训练数据的选取也是很关键的, 良好的训练数据本身的局部特征应尽可能少, 噪声也尽可能小 .
6、L1和L2正则的区别,如何选择L1和L2正则
L0正则化的值是模型参数中非 零参数的个数。
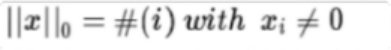
也就是如果我们使用 L0范数 ,即希望w的大 部分元素都是0. ( w是稀疏的)所以可以用 于ML中做稀疏编码,特征选择。通过最小 化L0范数 ,来寻找最少最优的稀疏特征项。但不幸的是, L0范数的最优化问题是— 个NP hard问题, 而 且理论上有证明, L1范数是L0范数的最优凸近似, 因此通常使用 L1范数来代替。
L1正则化表示各个参数绝对值之和。
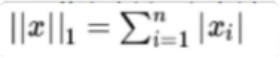
L1范数的解通常是稀疏性的 ,倾向于选择数目 较少的— 些非 常大 的值或者数目 较多的insignificant的小值。
L2正则化标识各个参数的平方 的和的开方 值。

L2范数越小 ,可以使得w的每个元素都很小 ,接近于0 ,但L1范数不同的是他不会让它等于0而 是接近于0.




)





)



)

)


