探秘信道的极限容量：从奈氏准则到香农定理

在数字通信的世界里，我们常常会思考一个问题：信道究竟能以多快的速度传输数据？这个问题的答案，就藏在信道的极限容量之中。今天，就让我们一起来了解影响它的关键因素和重要定理。

一、信道极限容量的基本概念🤔

 数字通信中，信道容量 指在指定噪声和带宽条件下，信道能可靠传输信息的最大速率。实际信道因物理特性限制，无法以任意高速率传输数据，其性能存在一个不可逾越的上限——这就是 信道极限容量。

数字通信的核心优势在于抗干扰能力：即使信号在传输过程中发生失真，只要接收端能够正确识别出原始码元（0或1），通信仍然可以成功。

而信号在传输过程中因信道带宽、噪声等因素产生波形扭曲，称为 失真。失真分为可恢复的失真 和 不可恢复的失真，其可恢复性取决于信号的信噪比和码元间隔。

一般来说，码元的传输速率越高、信号的传输距离越远、噪声干扰越大或者传输介质的质量越差，接收端波形的失真就越严重。

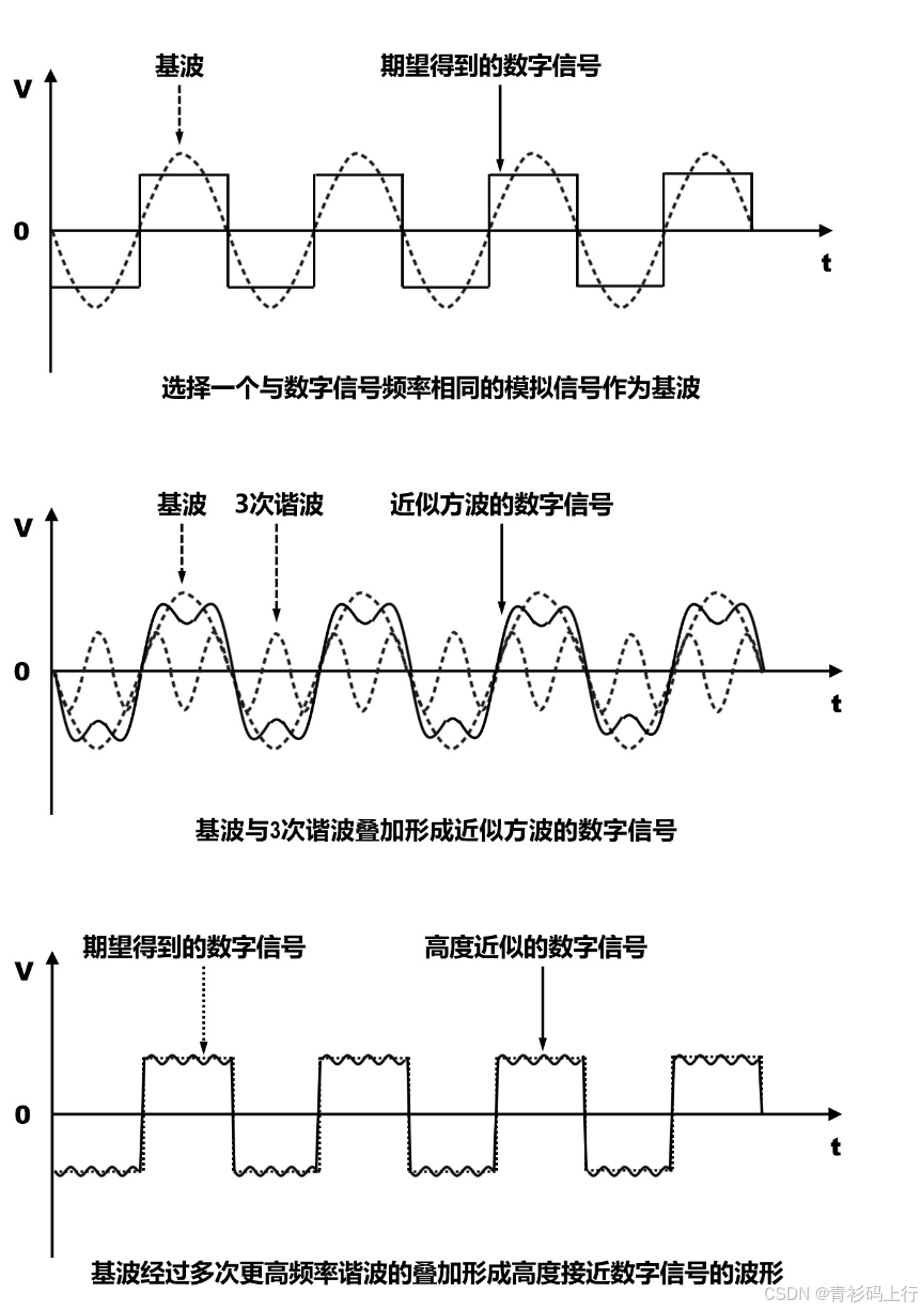
 图形解释：数字信号（方波）的本质是基波 + 高次谐波的叠加，信道带宽决定了能传输的谐波次数 —— 谐波次数越少，信号越圆滑（失真越严重）；谐波次数越多，信号越接近理想方波（失真越小）。 这就是数字信号传输中 “失真” 的底层原理，也是为什么通信要讲究 “带宽匹配” 的原因

二、奈氏准则：无噪声情况下的码元速率限制🐦‍🔥

（一）带宽与信号传输的关系

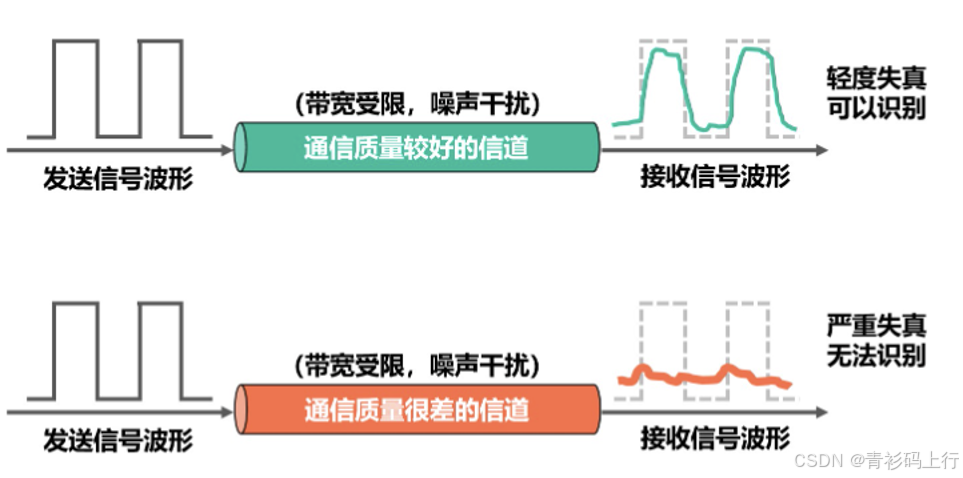
信道的物理特性决定了其能通过的信号频率范围。信道的带宽（W） 指其能通过的有效频率范围（如0~4000Hz）。信号中的高频分量在传输时会被信道衰减或滤除，导致波形失真。

若信道带宽不足，高频分量会被衰减，信号波形的陡峭边沿（上升沿和下降沿）会变得平缓，甚至出现“拖尾”现象。

（二）码间串扰问题

当相邻码元的波形因高频分量衰减或者丢失而发生重叠时，接收端难以区分每个码元的界限，就会导致误码，这种现象称为 码间串扰

（三）奈氏准则的内容

1924年，奈奎斯特提出了著名的奈氏准则，其关键条件是：

• 适用于低通型信道（如电话线、光纤，带宽范围0～max）
• 不考虑噪声，仅关注信号失真（但实际信道中存在噪声，因此很难达到最高上限）

奈氏准则得出了以下结论：

1. 在任何信道中，码元传输速率是有上限的。若传输速率超过上限，则会出现严重的码间串扰问题，使得接收端无法完全正确地识别码元
2. 信道的带宽越大，则传输码元的能力越强
3. 奈氏准则给出了码元传输速率的限制，但并未限制信息传输速率，即未对一个码元最多可以携带多少比特给出限制

三、香农定理：有噪声情况下的信息传输速率限制🐦‍🔥

（一）信噪比的概念

要了解香农定理，首先需要知道信噪比。信噪比 是信号的平均功率与噪声的平均功率之比，其中S为信道内所传输信号的平均功率，N为信道内的高斯噪声功率。

信噪比有两种表示形式：

• 无单位记法：信噪比=S/N
• 分贝（dB）记法：当采用这种记法时，需要进行单位转换，例如当S/N=1000时，信噪比为30dB。

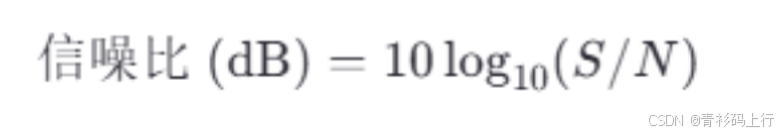
（二）香农定理的内容

1948年，香农（Shannon）提出了著名的香农公式：

注意：在使用香农定理计算信道的极限数据传输速率时，信噪比应采用无单位记法。
 香农公式表达了一个绝对极限，即任何通信系统都无法突破此速率上限。实际信道中能够达到的信息传输速率，要比香农公式给出的极限传输速率低不少，因为实际信道中信号还要受到其他一些损伤，如各种脉冲干扰和信号衰减等，这些因素在香农公式中并未考虑。

四、奈氏准则与香农定理的对比与应用🌰

 奈氏准则指出，无噪声信道的最大码元速率为2W码元/秒。在实际系统中，我们可以通过多电平编码让每个码元携带更多比特信息，从而提升数据传输速率。但香农公式设定了最终的数据传输速率上限，无法通过单纯增加编码复杂度突破，也就是说：一个码元能携带的比特数是有限的。

简单来说，无噪声/理想信道适用奈氏准则；有噪声/非理想信道适用香农定理。

在实际应用中，有几点需要注意：

1. 对于奈氏准则，公式2W算出的是波特率，题目一般还会给出每个码元的离散电平数量，需要先算出一个码元可携带的信息量，再根据波特率算出比特率。
2. 对于香农公式，题目一般会给出分贝记法的信噪比，做题时记得先化为无单位记法的数值。

---

如果我的内容对你有帮助，请 点赞 ， 评论 ， 收藏 。创作不易，大家的支持就是我坚持下去的动力！