一、问题描述

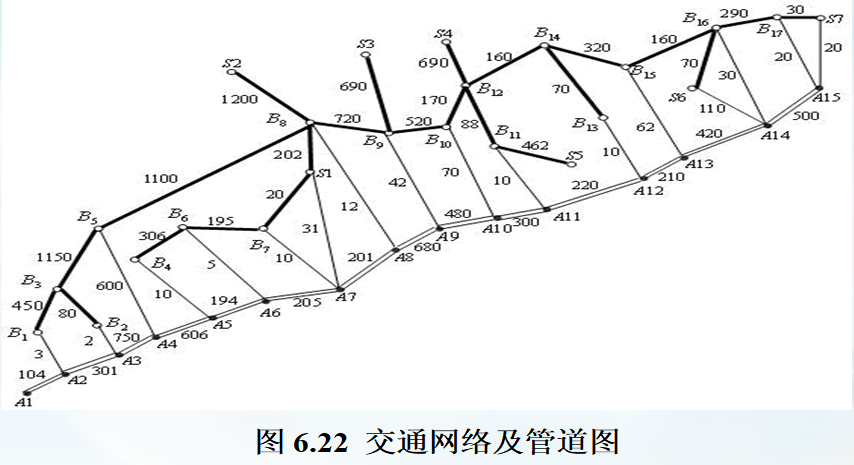
要铺设一条 $A1→A2→⋯→A15A_1 \rightarrow A_2 \rightarrow \cdots \rightarrow A_{15}$ 的输送天然气的主管道，如图 6.22 所示。经筛选后可以生产这种主管道钢管的钢厂有 $S1,S2,⋯,S7S_1, S_2, \cdots, S_7$ 。图中粗线表示铁路，单细线表示公路，双细线表示要铺设的管道（假设沿管道或者原来有公路，或者建有施工公路），圆圈表示火车站，每段铁路、公路和管道旁的阿拉伯数字表示里程（单位 km）。
在这里插入图片描述
为方便计，1km 主管道钢管称为 1 单位钢管。

一个钢厂如果承担制造这种钢管，至少需要生产 500 个单位。钢厂 $S_i$ 在指定期限内能生产该钢管的最大数量为 $s_i$ 个单位，钢管出厂销价 1 单位钢管为 $p_i$ 万元，见表 6.9；1 单位钢管的铁路运价见表 6.10。

							表 6.9 各钢管厂的供货上限及销价

i	1	2	3	4	5	6	7
$s_i$	800	800	1000	2000	2000	2000	3000
$p_i$	160	155	155	160	155	150	160

							表 6.10 单位钢管的铁路运价

里程(km)	≤300	301~350	351~400	401~450	451~500
运价(万元)	20	23	26	29	32
里程(km)	501~600	601~700	701~800	801~900	901~1000
运价(万元)	37	44	50	55	60

1000km 以上每增加 1 至 100km 运价增加 5 万元。公路运输费用为 1 单位钢管每公里 0.1 万元（不足整公里部分按整公里计算）。钢管可由铁路、公路运往铺设地点（不只是运到点 $A1,A2,⋯,A15A_1, A_2, \cdots, A_{15}$ ，而是管道全线）请制定一个主管道钢管的订购和运输计划，使总费用最小（给出总费用）。

二、问题分析

问题的建模目的是求一个主管道钢管的订购和运输策略，使总费用最小。首先，问题给出了 7 个供选择的钢厂，选择哪些？订购多少？是一个要解决的问题。其次，每一个钢厂到铺设地点大多都有多条可供选择的运输路线，应选择哪一条路线运输，取决于建模的目标。而目标总费用包含两个组成部分：订购费用和运输费用。订购费用取决于单价和订购数量，运输费用取决于往哪里运和运输路线。结合总目标的要求，可以很容易地想到应选择运费最小的路线。
从同一个钢管厂订购钢管运往同一个目的地，一旦最小运输费用路线确定，则单位钢管的运费就确定了，单位钢管的订购及运输费用=钢管单价+运输费用。因此，同一个钢管厂订购钢管运往同一个目的地的总费用等于订购数量乘以单位钢管的购运费用（单价+单位钢管运费）。因而，在制定订购与运输计划时，要分成两个子问题考虑：

(1)运输路线及运输费用的确定：钢管可以通过铁路或公路运输，公路运费是运输里程的线性函数，但是铁路运价却是一种分段的阶跃的常数函数。因此在计算时，不管对运输里程还是费用而言，都不具有可加性，只能将铁路运价（即由运输总里程找出对应费率）和公路运价分别计算后再叠加。

(2)铺设方案的设定：从钢管厂订购若干个单位的钢管运送至枢纽点 $A1,A2,⋯,A15A_{1}, A_{2}, \cdots, A_{15}$ ，再由枢纽点按一个单位计分别往枢纽点两侧运送至最终铺设地点，计算从枢纽点开始的铺设费用。

虽然准备把问题分解为两个子问题进行处理，但最终优化时，必须作为一个综合的优化问题进行处理，否则无法得到全局最优解。

三、模型的建立与求解

记第 $\cdots, 7)$ 个钢厂的最大供应量为 $s_{i}$ ，从第 i 个钢厂到铺设节点 $\cdots, 15)$ 的订购和运输费用为 $c_{ij}$ ；用 $lk=∣AkAk+1∣(k=1,2,⋯,14)l_{k}=|A_{k}A_{k+1}|(k=1, 2, \cdots, 14)$ 表示管道第 k 段需要铺设的钢管量。 $x_{ij}$ 是从钢厂 $S_{i}$ 运到节点 j 的钢管量， $y_{j}$ 是从节点 j 向左铺设的钢管量， $z_{j}$ 是从节点 j 向右铺设的钢管量。

根据题中所给数据，可以先计算出从供应点 $S_{i}$ 到需求点 $A_{j}$ 的最小购运费 $c_{ij}$ （即出厂售价与运输费用之和），再根据 $c_{ij}$ 求解总费用，总费用应包括：订购费用（已包含在 $c_{ij}$ 中），运输费用（由各厂 $S_{i}$ 经铁路、公路至各点 $Aj,i=1,2,⋯,7A_{j}, i=1, 2, \cdots, 7$ ），铺设管道 $A_{j}A_{j+1}(j=1, 2, L, 14)$ 的运费。

1.运费矩阵的计算模型

购买单位钢管及从 $S_{i}(i=1, 2, L, 7)$ 运送到 $A_{j}(j=1, 2, L, 15)$ 的最小购运 $j = 1, 2, L, 15$ 费用 $c_{ij}$ 的计算如下。

(1)计算铁路任意两点间的最小运输费用

由于铁路运费不是连续的，故不能直接构造铁路费用赋权图，用 Floyd 算法来计算任意两点间的最小运输费用。但可以首先构造铁路距离赋权图，用 Floyd 算法来计算任意两点间的最短铁路距离值，再依据题中的铁路运价表，求出任意两点间的最小铁路运输费用。这就巧妙地避开铁路运费不是连续的问题。
首先构造铁路距离赋权图 $G_{1}=(V, E_{1}, W_{1})$ ，其中 $V={S1,⋯,S7,A1,⋯,A15,B1,⋯,B17}={v1,v2,⋯,v39}V=\{S_{1}, \cdots, S_{7}, A_{1}, \cdots, A_{15}, B_{1}, \cdots, B_{17}\}=\{v_{1}, v_{2}, \cdots, v_{39}\}$ ，总共 39 个顶点的编号见图 6.22； $W1=(wij(1))39×39W_{1}=(w_{ij}^{(1)})_{39\times 39}$ ，

$wij(1)={dij(1),vi,vj之间有铁路直接相连+∞,vi,vj之间没有铁路直接相连\boldsymbol {w}_{ij}^{(1)}=\left \{ \begin{aligned} &\boldsymbol {d}_{ij}^{(1)}, \boldsymbol {v}_{i},\boldsymbol {v}_{j}之间有铁路直接相连\\ &+\infty , \boldsymbol {v}_{i},\boldsymbol {v}_{j}之间没有铁路直接相连\end{aligned} \right .$
式中： $d_{ij}^{(1)}$ 表示 $v_{i}, v_{j}$ 两点之间的铁路里程。然后应用Floyd算法求得任意两点间的最短铁路距离。
根据铁路运价表，可以得到铁路费用赋权完全图 $G~1=(V,E1,W~1)\widetilde{G}_{1}=(V, E_{1}, \widetilde{W}_{1})$ , 其中 $W~1=(cij(1))39×39\widetilde{W}_{1}=(c_{ij}^{(1)})_{39\times 39}$ ,这里 $c_{ij}^{(1)}$ 为第 i , j 顶点间的最小铁路运输费用，若两点间的铁路距离值为无穷大，则对应的铁路运输费用也为无穷大。

(2) 构造公路费用的赋权图

构造公路费用赋权图 $G_{2}=(V, E_{2}, W_{2})$ ，其中 V 同上， $W2=(cij(2))39×39W_{2}=(c_{ij}^{(2)})_{39\times 39}$

$cij(2)={0.1dij(2),vi,vj之间有公路相连，+∞,vi,vj之间没有公路相连，c_{ij}^{(2)}=\left \{ \begin{aligned} &0.1d_{ij}^{(2)},v_{i},v_{j}之间有公路相连，\\ &+\infty ,v_{i},v_{j}之间没有公路相连，\end{aligned} \right .$
式中： $d_{ij}^{(2)}$ 表示 $v_{i}, v_{j}$ 两点之间的公路里程。

(3)计算任意两点间的最小运输费用

由于可以用铁路、公路交叉运送，所以任意相邻两点间的最小运输费用为铁路、公路两者最小运输费用的最小值。

构造铁路公路的混合赋权图 $W=(c_{ij}^{(3)})_{39\times 39}$ ，其中 $c_{ij}^{(3)}=min(c_{ij}^{(1)}, c_{ij}^{(2)})$ 。

对图G应用Floyd算法，就可以计算出所有顶点对之间的最小运输费用，最后提取需要的 $Si(i=1,2,⋯,7)S_{i}(i=1, 2, \cdots, 7)$ 到 $Aj(j=1,2,⋯,15)A_{j}(j=1, 2, \cdots, 15)$ 的最小运输费用 $c~ij\widetilde{c}_{ij}$ （单位：万元）见表6.11。

									表6.11 最小运费计算结果

170.7	160.3	140.2	98.6	38	20.5	3.1	21.2	64.2	92	96	106	121.2	128	142
215.7	205.3	190.2	171.6	111	95.5	86	71.2	114.2	142	146	156	171.2	178	192
230.7	220.3	200.2	181.6	121	105.5	96	86.2	48.2	82	86	96	111.2	118	132
260.7	250.3	235.2	216.6	156	140.5	131	116.2	84.2	62	51	61	76.2	83	97
255.7	245.3	225.2	206.6	146	130.5	121	111.2	79.2	57	33	51	71.2	73	87
265.7	255.3	235.2	216.6	156	140.5	131	121.2	84.2	62	51	45	26.2	11	28
275.7	265.3	245.2	226.6	166	150.5	141	131.2	99.2	76	66	56	38.2	26	2

任意两点间的最小运输费用加上出厂售价，得到单位钢管从任一个 $Si(i=1,2,⋯,7)S_{i}(i=1, 2, \cdots, 7)$ 到 $Aj(j=1,2,⋯,15)A_{j}(j=1, 2, \cdots, 15)$ 的购买和运送最小费用 $c_{ij}$ 。

2.总费用的数学规划模型

目标函数

(1) 从钢管厂到各枢纽点 $A_{1}$ , $A2,⋯,A15A_{2}, \cdots, A_{15}$ 的总购运费用为 $∑i=17∑j=115cijxij\sum \limits _{i=1}^{7}\sum \limits _{j=1}^{15}c_{ij}x_{ij}$
(2)铺设管道不仅只运输到枢纽点，而是要运送并铺设到全部管线，注意到将总量为y $_{j}$ 的钢管从枢纽点往左运到每单位铺设点，其运费应为第一公里、第二公里、 $⋯⋯\cdots \cdots$ 直到第y $_{j}$ 公里的运费之和，即为
$0.1×(1+2+⋯+yj)=0.12yj(yj+1).\mathbf 0.1\times (1+2+\cdots +y_{j})=\frac {0.1}{2}y_{j}(y_{j}+1).$
从枢纽点 $A_{j}$ 往右也一样，对应的铺设费用为
$0.1×(1+2+⋯+zj)=0.12zj(zj+1).0.1\times (1+2+\cdots +z_{j})=\frac{0.1}{2}z_{j}(z_{j}+1).$
总的铺设费用为
$0.12∑j=115[yj(yj+1)+zj(zj+1)].\frac{0.1}{2}\sum _{j=1}^{15}[y_{j}(y_{j}+1)+z_{j}(z_{j}+1)].$
因而，总购运费用为
$∑i=17∑j=115cijxij+0.12∑j=115[yj(yj+1)+zj(zj+1)]\sum _{i=1}^{7}\sum _{j=1}^{15}c_{ij}x_{ij}+\frac{0.1}{2}\sum _{j=1}^{15}[y_{j}(y_{j}+1)+z_{j}(z_{j}+1)]$

约束条件
(1) 根据钢管厂生产能力约束或购买限制，有
$∑j=115xij∈{0}∪[500,si],i=1,2,⋯,7.\sum_{j=1}^{15} x_{ij} \in \{0\} \cup [500, s_i], \quad i = 1, 2, \cdots, 7.$

(2) 购运量应等于铺设量
$∑i=17xij=zj+yj,j=1,2,⋯,15.\sum_{i=1}^{7} x_{ij} = z_j + y_j, \quad j = 1, 2, \cdots, 15.$

(3) 枢纽点间距约束：从两个相邻枢纽点分别往右、往左铺设的总单位钢管数应等于其间距，即
$zj+yj+1=∣AjAj+1∣=lj,j=1,2,⋯,14.z_j + y_{j+1} = |A_j A_{j+1}| = l_j, \quad j = 1, 2, \cdots, 14.$

(4) 端点约束：

从枢纽点 $A_{1}$ 只能往右铺，不能往左铺，故
$y_{1} = 0,$
从枢纽点 $A_{15}$ 只能往左铺，不能往右铺，故
$z_{15} = 0.$

(5) 非负约束：
$xij≥0,yj≥0,zj≥0,i=1,2,⋯,7,j=1,2,⋯,15.x_{ij} \ge 0, \quad y_{j} \ge 0, \quad z_{j} \ge 0, \quad i=1, 2, \cdots, 7, \quad j=1, 2, \cdots, 15.$

综上所述，建立如下数学规划模型

$min⁡∑i=17∑j=115cijxij+0.12∑j=115(zj(zj+1)+yj(yj+1)),(6.25)\min\sum _{i=1}^{7}\sum _{j=1}^{15}c_{ij}x_{ij}+\frac {0.1}{2}\sum _{j=1}^{15}(z_{j}(z_{j}+1)+y_{j}(y_{j}+1)),(6.25)$

s.t.
${∑j=115xij∈{0}∪[500,si],i=1,2,⋯,7,∑i=17xij=zj+yj,j=1,2,⋯,15,zj+yj+1=lj,j=1,2,⋯,14,y1=0,z15=0,xij≥0,yj≥0,zj≥0,i=1,2,⋯,7;j=1,2,⋯,15.(6.26)\left \{ \begin{aligned} &\sum _{j=1}^{15}x_{ij}\in \{ 0\} \cup [500,s_{i}], & i=1,2,\cdots ,7,\\ &\sum _{i=1}^{7}x_{ij}=z_{j}+y_{j}, & j=1,2,\cdots ,15,\\ &z_{j}+y_{j+1}=l_{j}, & j=1,2,\cdots ,14,\\ &y_{1}=0, z_{15}=0,\\ &x_{ij}\ge 0, y_{j}\ge 0, z_{j}\ge 0, & i=1,2,\cdots ,7; j=1,2,\cdots ,15. \end{aligned} \right .(6.26)$

3.模型求解

使用计算机求解上述数学规划时，需要对约束条件（6.26）中的第一个非线性约束

$∑j=115xij∈{0}∪[500,si],i=1,2,⋯,7(6.27)\sum _{j=1}^{15}x_{ij}\in \{ 0\} \cup [500,s_{i}], \quad i=1,2,\cdots ,7 \quad (6.27)$
进行处理。引进0-1变量

$i不生产,t_{i}=\left \{ \begin{matrix} 1, & \text{钢管厂 } i \text{ 生产}, \\ 0, & \text{钢管厂 } i \text{ 不生产}, \end{matrix} \right .$
把约束条件(6.27)转化为线性约束

$500ti≤∑j=115xij≤siti,i=1,2,⋯,7.(6.28)500t_{i}\le \sum _{j=1}^{15}x_{ij}\le s_{i}t_{i}, \quad i=1,2,\cdots ,7. \quad (6.28)$

利用 Python 软件求得总费用的最小值为 127.8632 亿。具体的订购和运输方案见表 6.12 所示。

	订购量	$A_{2}$	$A_{3}$	$A_{4}$	$A_{5}$	$A_{6}$	$A_{7}$	$A_{8}$	$A_{9}$	$A_{10}$	$A_{11}$	$A_{12}$	$A_{13}$	$A_{14}$	$A_{15}$
$S_{1}$	800	0	0	319	15	200	266	0	0	0	0	0	0	0	0
$S_{2}$	800	179	321	0	0	0	0	300	0	0	0	0	0	0	0
$S_{3}$	1000	0	187	149	0	0	0	0	664	0	0	0	0	0	0
$S_{4}$	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
$S_{5}$	1015	0	0	0	600	0	0	0	0	0	415	0	0	0	0
$S_{6}$	1556	0	0	0	0	0	0	0	0	351	0	86	333	621	165
$S_{7}$	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

钢管运输excel文件：https://wwo.lanzouu.com/igf7E33r9uha 密码:1gni
相应的python代码如下：

#程序文件anli6_1.py
import cvxpy as cp
import numpy as np
import networkx as nx
import pandas as pds1 = ['S'+str(i) for i in range(1,8)]
s2 = ['A'+str(i) for i in range(1,16)]
s3 = ['B'+str(i) for i in range(1,18)]
L = s1 + s2 + s3   #构造顶点字符列表
G1 = nx.Graph(); G1.add_nodes_from(L)
L1 = [('B1','B3',450),('B2','B3',80),('B3','B5',1150),('B5','B8',1100),('B4','B6',306),('B6','B7',195),('S1','B7',20),('S1','B8',202),('S2','B8',1200),('B8','B9',720),('S3','B9',690),('B9','B10',520),('B10','B12',170),('S4','B12',690),('S5','B11',462),('B11','B12',88),('B12','B14',160),('B13','B14',70),('B14','B15',320),('B15','B16',160),('S6','B16',70),('B16','B17',290),('S7','B17',30)]
G1.add_weighted_edges_from(L1)  #构造铁路赋权图
d1 = nx.floyd_warshall_numpy(G1) #求最短距离矩阵
d1 = np.array(d1)  #转换为array数组
c1 = np.ones(d1.shape)*np.inf
c1[d1==0]=0; c1[(d1>0) & (d1<=300)]=20
c1[(d1>300) & (d1<=350)]=23; c1[(d1>350) & (d1<=400)]=26
c1[(d1>400) & (d1<=450)]=29; c1[(d1>450) & (d1<=500)]=32
c1[(d1>500) & (d1<=600)]=37; c1[(d1>600) & (d1<=700)]=44
c1[(d1>700) & (d1<=800)]=50; c1[(d1>800) & (d1<=900)]=55
c1[(d1>900) & (d1<=1000)]=60; ind=(d1>1000) & (d1<np.inf)
c1[ind]=60+5*np.ceil(d1[ind]/100-10)G2 = nx.Graph()
G2.add_nodes_from(L)
L2 = [('A1','A2',104),('A2','B1',3),('A2','A3',301),('A3','B2',2),('A3','A4',750),('A4','B5',600),('A4','A5',606),('A5','B4',10),('A5','A6',194),('A6','B6',5),('A6','A7',205),('A7','B7',10),('S1','A7',31),('A7','A8',201),('A8','B8',12),('A8','A9',680),('A9','B9',42),('A9','A10',480),('A10','B10',70),('A10','A11',300),('A11','B11',10),('A11','A12',220),('A12','B13',10),('A12','A13',210),('A13','B15',62),('A13','A14',420),('S6','A14',110),('A14','B16',30),('A14','A15',500),('A15','B17',20),('S7','A15',20)]
G2.add_weighted_edges_from(L2)  #构造公路赋权图
c2 = nx.to_numpy_matrix(G2)  #导出图G2的邻接矩阵
c2 = np.array(c2)   #转换为array数组
c2[c2==0] = np.inf
c3 = np.minimum(c1, 0.1*c2)G3 = nx.Graph(c3)
c4 = nx.floyd_warshall_numpy(G3) #求最短距离矩阵
c5 = c4[:7,7:22]   #提出7行15列的运费数据
f = pd.ExcelWriter('anli6_1.xlsx')
pd.DataFrame(c5).to_excel(f, index=False)s = np.array([800, 800, 1000, 2000, 2000, 2000, 3000])
p = np.array([160, 155, 155, 160, 155, 150, 160])
b = np.array([104, 301, 750, 606, 194, 205, 201,680, 480, 300, 220, 210, 420, 500])
c = np.tile(p,(15,1)).T + c5  #购运费用
x = cp.Variable((7,15), integer=True)  #调整为整型
y = cp.Variable(15, pos=True); z = cp.Variable(15, pos=True)
t = cp.Variable(7, integer=True)
obj = cp.Minimize(cp.sum(cp.multiply(c, x))+0.05*cp.sum(y**2+y+z**2+z))
con = [500*t<=cp.sum(x,axis=1), cp.sum(x,axis=1)<=cp.multiply(s,t),cp.sum(x,axis=0)==y+z, y[1:]+z[:-1]==b,y[0]==0, z[14]==0,t>=0, t<=1, x>=0]
prob = cp.Problem(obj, con); prob.solve(solver='CPLEX')
print('最优值为：', prob.value); print('最优解为：\n', x.value)
sx = np.sum(x.value, axis=1)  
pd.DataFrame(c).to_excel(f, 'Sheet2', index=False)
pd.DataFrame(x.value).to_excel(f, 'Sheet3', index=False)
f.close()