1. 问题描述

我们现在写一个3D的Unity程序，我们现在设置了一个物体后，我们想旋转使其改为我们想要的情况。但是我们如果rotation输入了3个值后，我们发现现在旋转的时候，rotation的值会突然跳转变换到另一个值。这个时候我们修改例如x的值，y和z值也会随着x值发生变化。我们在这种情况下难以通过不断调整三个坐标轴的旋转将我们的物体旋转到我们想要的情况。

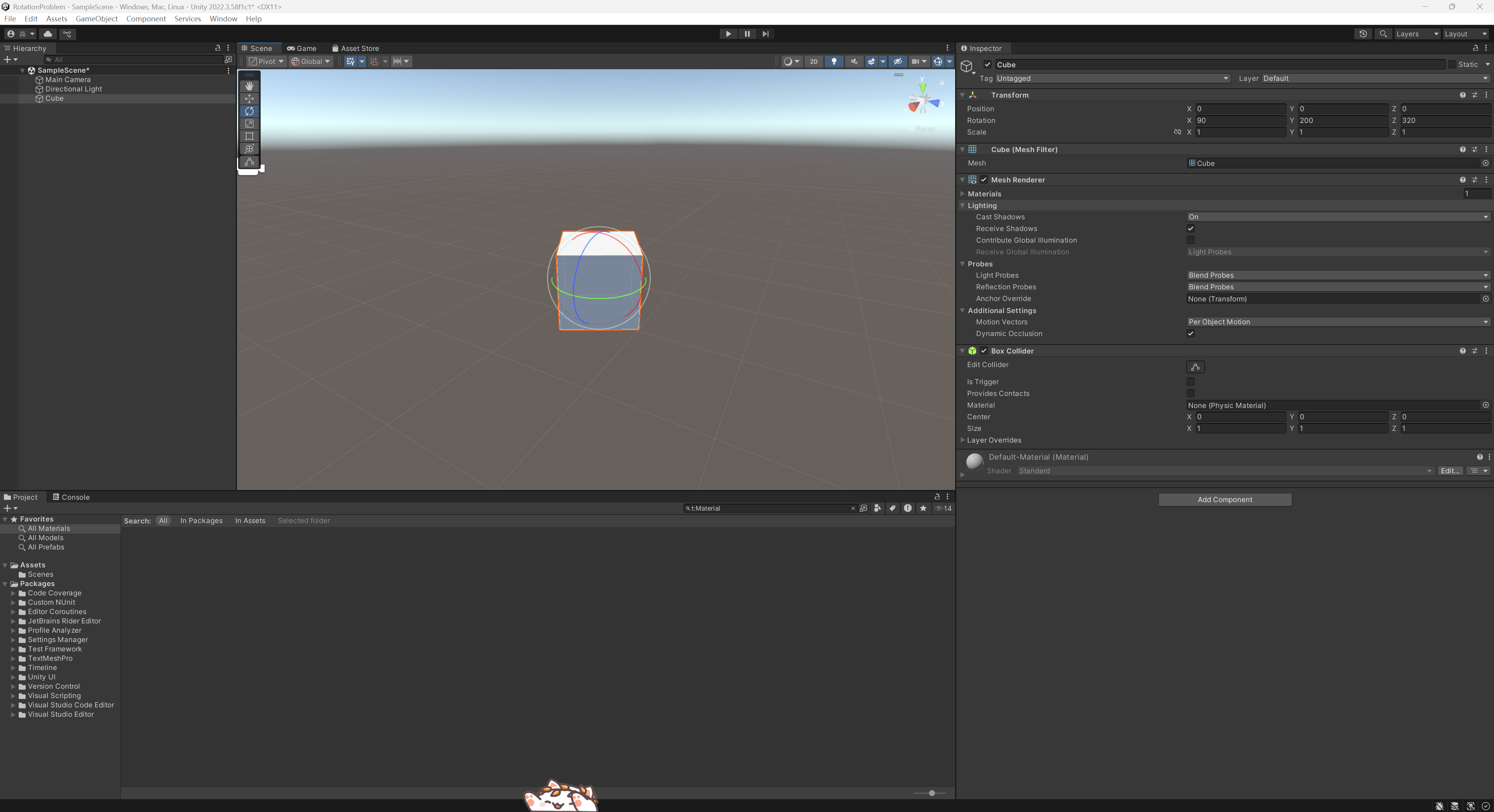
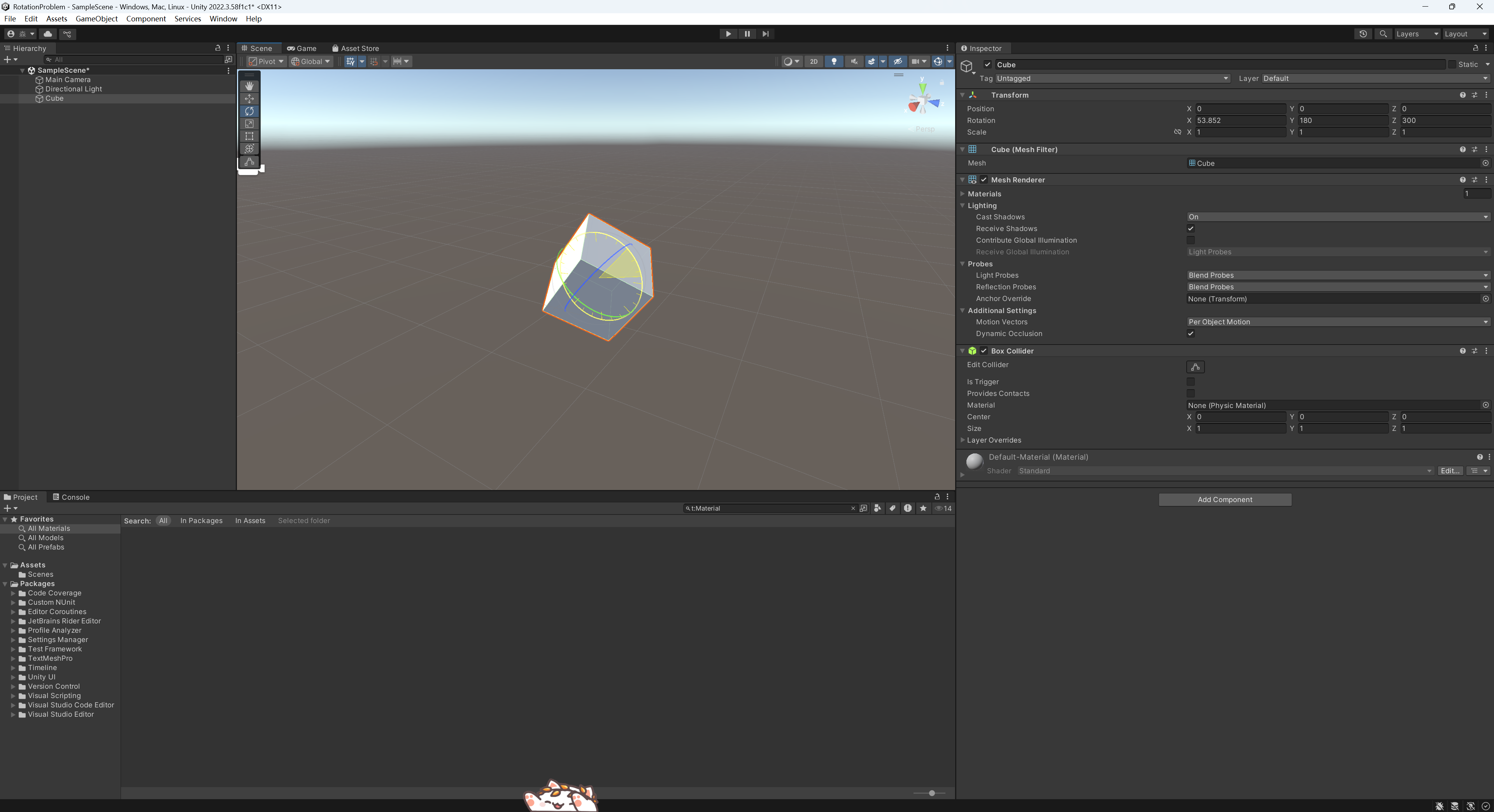
2. 问题原因

了解图形学的话，我们知道旋转（Rotation）是变换（Transformation）的一种，其底层计算使用矩阵来表示。
我们一般使用homogeneous co0ordinates（齐次坐标）来进行计算。
在三维空间中，绕z轴的旋转可以看作是在所有z坐标相同的平面上进行的二维旋转。
因此关于z轴旋转的情况如下：

关于y轴和x轴旋转的情况如下：

由于是矩阵计算，矩阵乘法有结合律但是没法使用交换律。
因此当我们完成了旋转之后，我们再次更改值，旋转顺序就被我们打乱了，因此矩阵的值会突然发生变化，此时我们再修改值，也不会是我们想象中的只变化一个轴的值，另外的值也会发生变化。

3. 解决方案

3.1通过多个父子关系从而控制旋转（推荐）

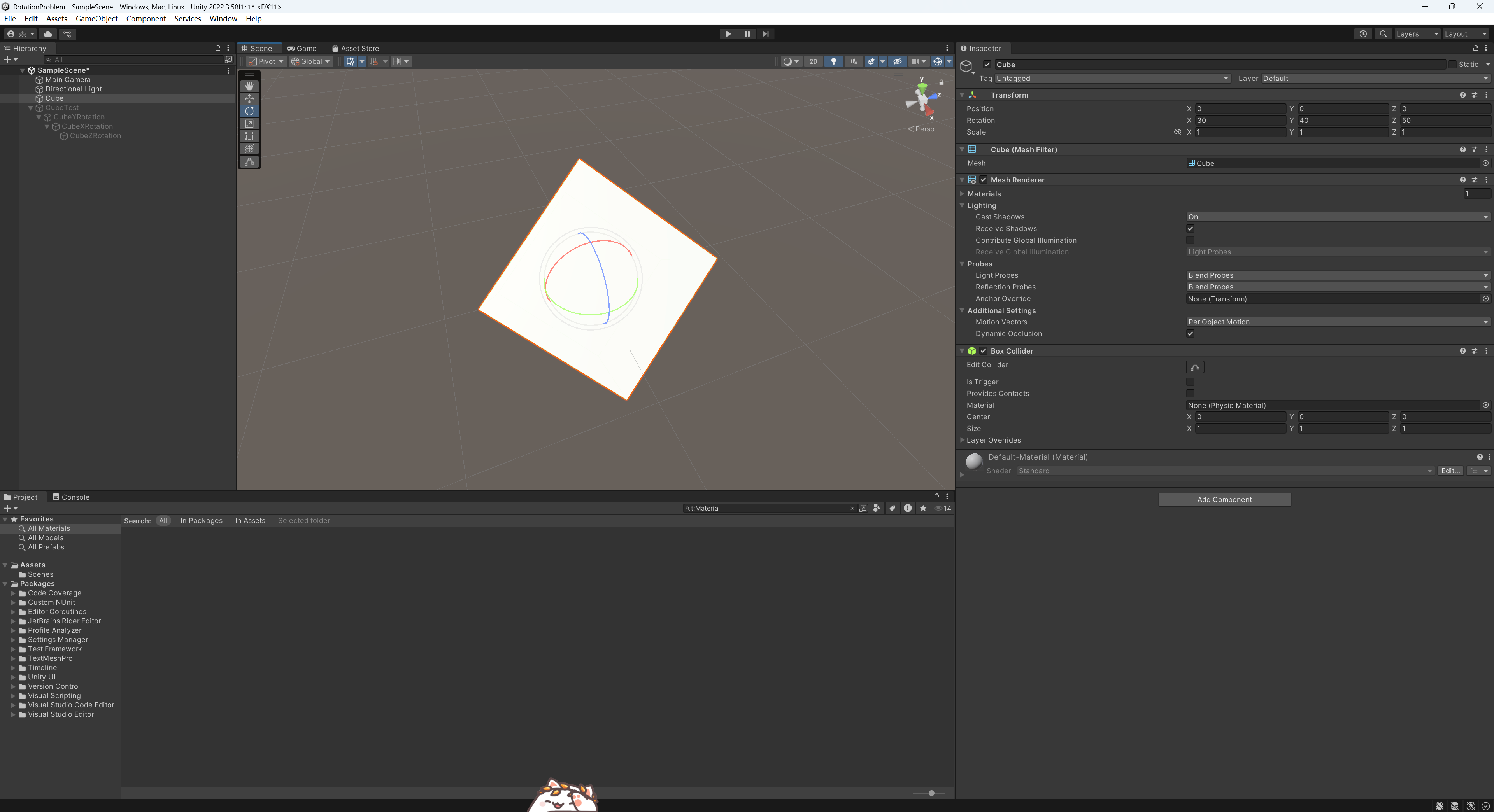
在 Unity中，旋转的顺序是先绕 Z 轴旋转，然后绕 X 轴旋转，最后绕 Y 轴旋转。也就是说，对于欧拉角 (30, 40, 50)，旋转顺序如下：

1. 先绕 Z 轴旋转 50°。
2. 再绕 X 轴旋转 30°。
3. 最后绕 Y 轴旋转 40°。

因此我们可以分别使用三个父子关系从而分别控制不同的轴进行旋转。
但是这里我们并不是Z轴在最外面作为父物体，而是Y轴在最外面作为父物体。
因为在 Unity 中使用父子关系来控制旋转时，每个子物体的旋转是相对于其父物体的局部坐标系进行的。在 Unity 中直接设置一个物体的欧拉角旋转时，这个旋转是相对于世界坐标轴的。
换句话说在Unity中根据自身坐标系旋转的顺序是Y-X-Z，根据世界坐标系旋转的顺序是Z-X-Y。所以这里正确的父子关系如图所示，顺序为Y-X-Z。

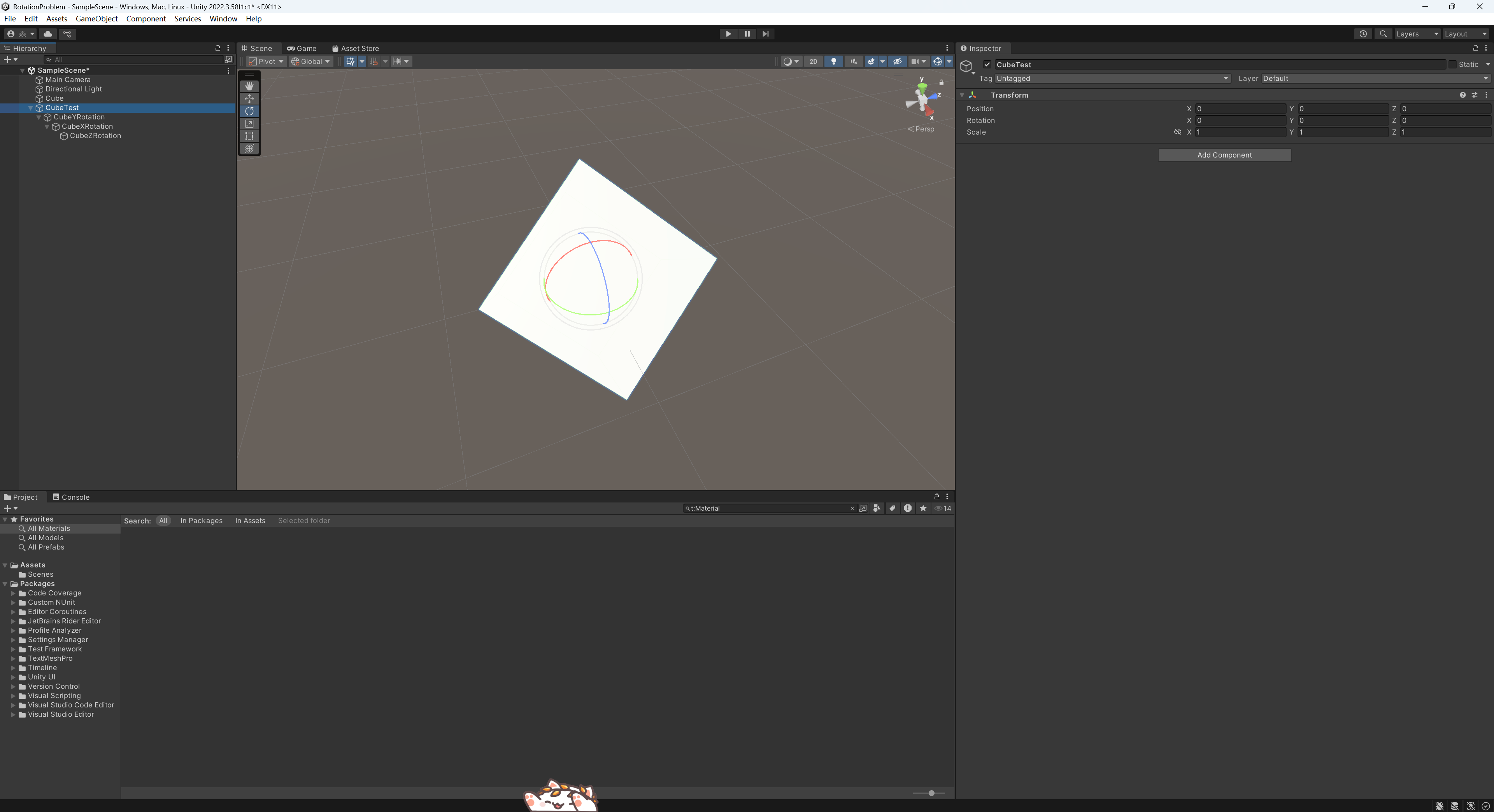
这里使用CubeYRotation控制Y轴的旋转。

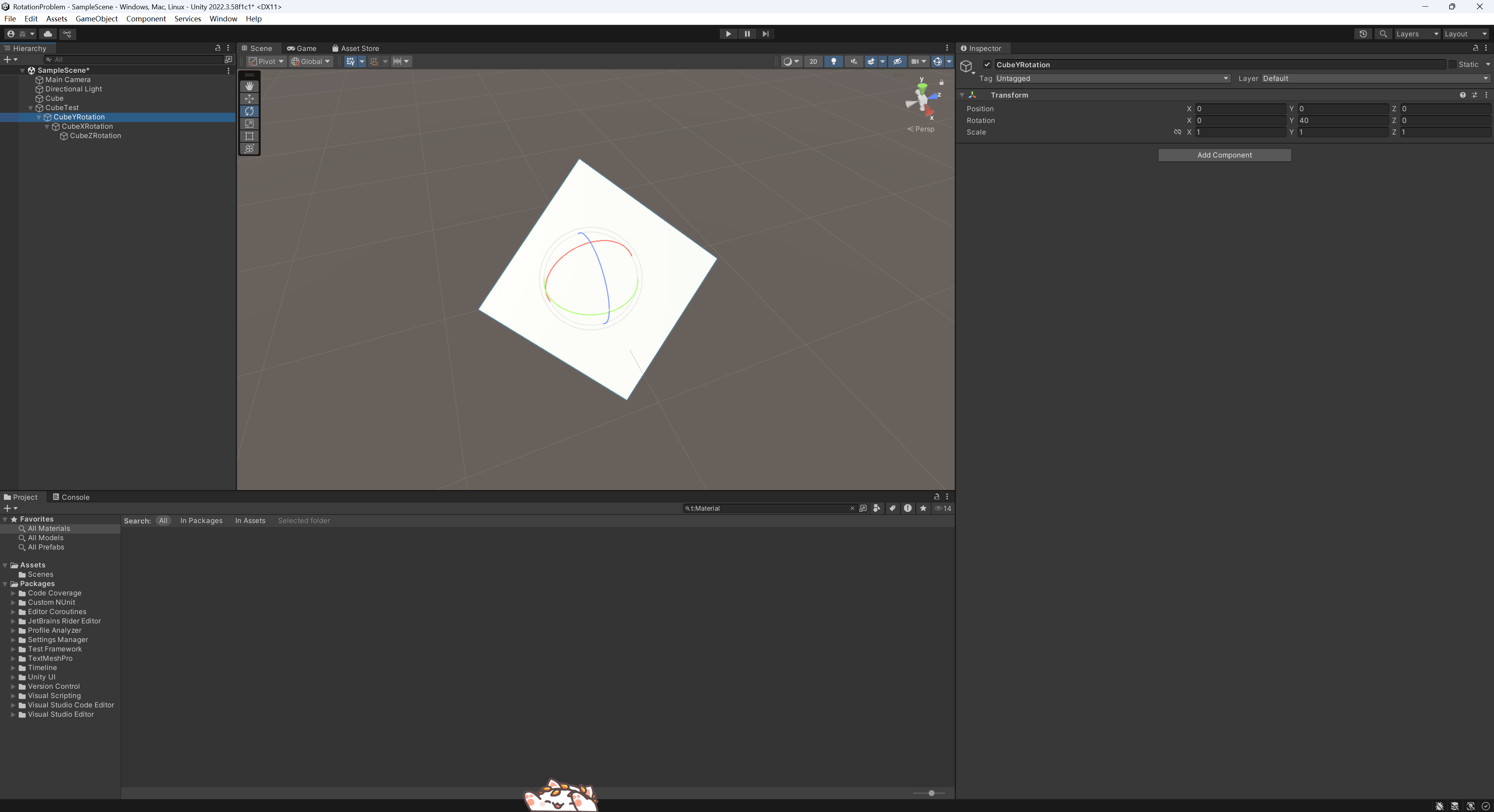
接着用其子物体CubeXRotation控制X轴的旋转。

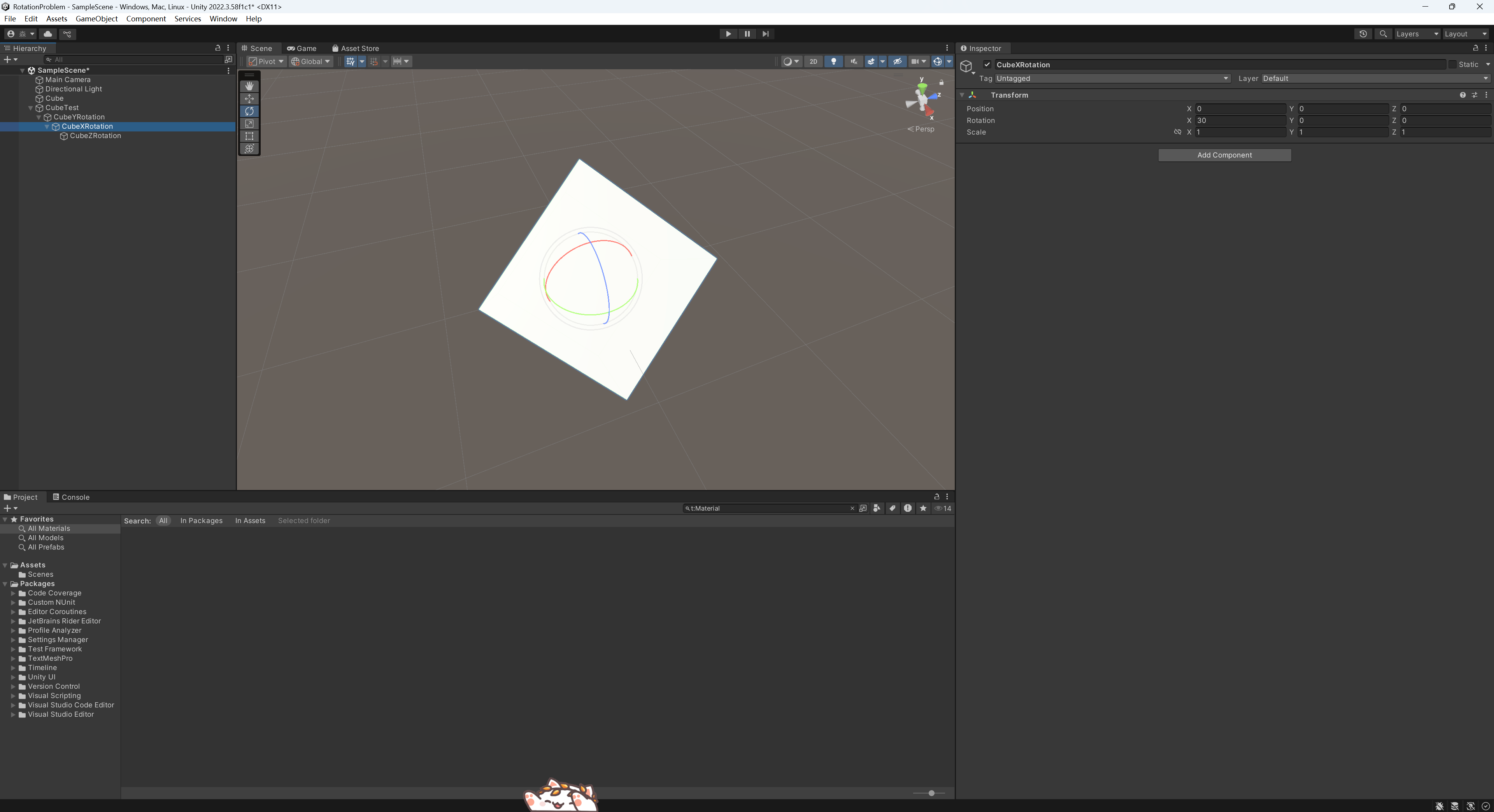
最后使用其子物体CubeZRotation控制Z轴的旋转。

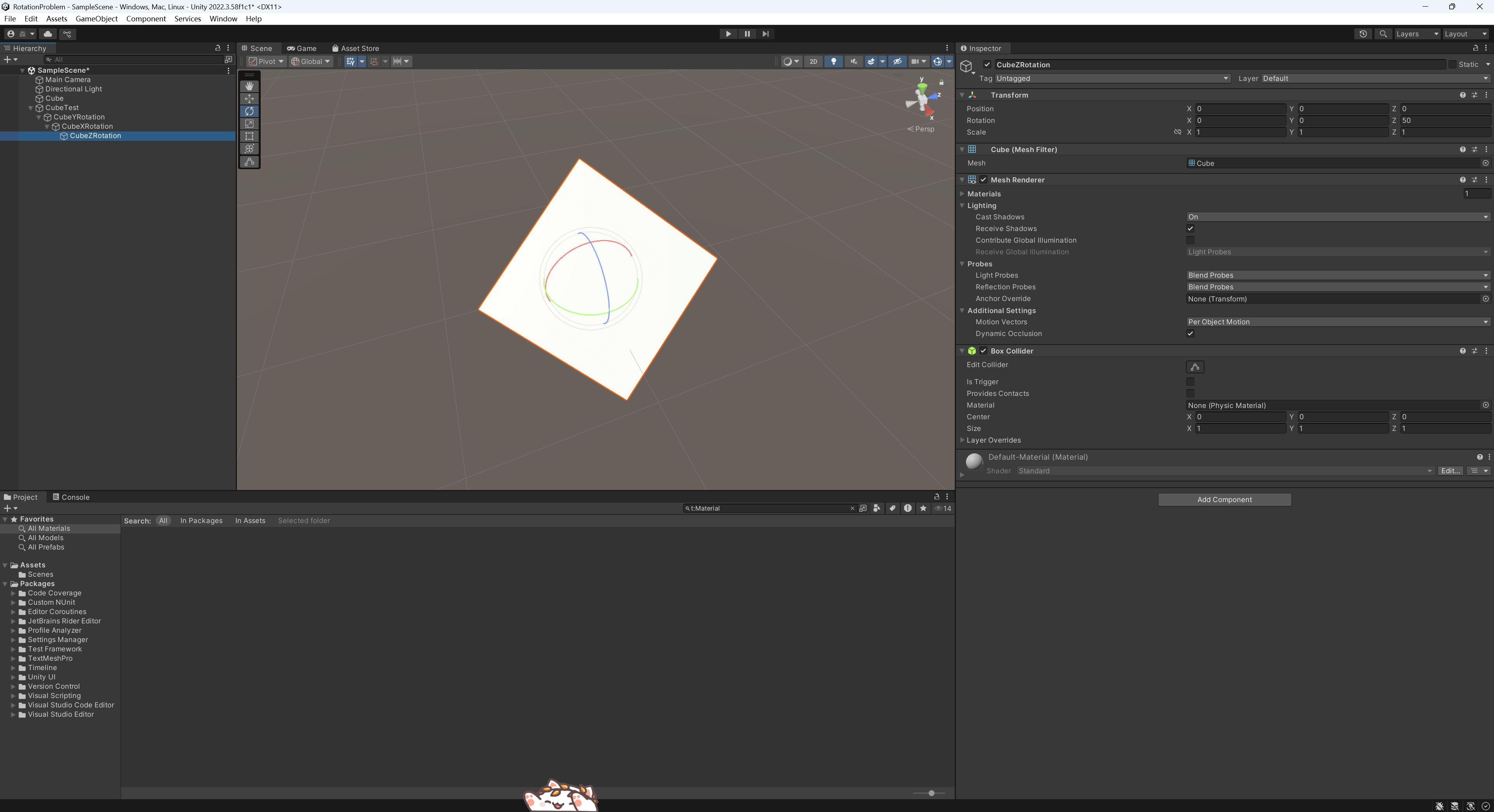
将其分别设置为和原来的Cube一样的旋转值，通过这样的方式我们可以得到和原来的Cube一样的效果，而且，这时候我们再分别旋转这些对象的Rotation可以只修改一个轴的Rotation，不会产生一次旋转多个值变化的情况。

这种方法易于控制，并且使用我们日常使用的欧拉角，所以方便理解，现实实践的时候可以不按照这个顺序进行控制，用这种父子关系控制旋转即可。
我们在实际使用Unity中也可以多使用父子关系控制对象的变换（包含位置、旋转、缩放），通过父子关系我们可以更好控制对象的位置关系和实际效果，还可以帮助我们更好管理对象的层级结构。
如图所示，我将这个场景里的所有对象放在了一个大的父物体下，方便控制。

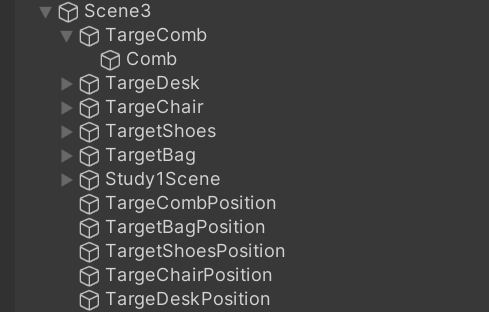
为了验证前面我们的结论我们可以试验下面的几个代码。
第一个代码：

transform.Rotate(45, 45, 45);

第二个代码：

transform.Rotate(0, 0, 45, Space.World);
transform.Rotate(45, 0, 0, Space.World);
transform.Rotate(0, 45, 0, Space.World);

第三个代码：

transform.Rotate(0, 45, 0);
transform.Rotate(45, 0, 0);
transform.Rotate(0, 0, 45);

这三个代码的效果一样，也能说明在Unity中根据自身坐标系旋转的顺序是Y-X-Z，根据世界坐标系旋转的顺序是Z-X-Y。

3.2 使用四元数进行旋转

如果我们学习Unity的教程，一般会告诉你旋转Unity采取四元数来表示和计算旋转，因为四元数不会像欧拉角一样存在万向锁（万向锁是使用欧拉角表示旋转时可能遇到的一个问题，即当旋转到某些特定角度时，会失去一个维度的自由度，导致旋转变得不稳定。）和表达方式多样的问题（欧拉角有无数种表达方式，这可能导致在计算或存储时出现混淆或错误）。
但是它并没有欧拉角那样易于理解，这里只稍微说下简单的概念。
它是一种扩展了复数的概念，可以表示为一个实部和三个虚部的组合，通常表示为 $q=w+xi+yj+zk$，其中$w,x,y,z$是实数，而$i,j,k$是虚数单位。这里实部与旋转的余弦值有关，虚部与旋转轴的方向向量有关。
四元数可以表示为：$q=cos(\theta /2)+(u\cdot i)sin(\theta /2)$其中，$\theta$是旋转角度， $u$是旋转轴的单位向量。

我们这里使用四元数进行旋转，这是Unity比较推荐的方式。
我们先创建三个旋转四元数，分别对应 X、Y、Z 轴的旋转角度。然后将这三个四元数相乘，得到最终的旋转四元数。将这里的最终四元数赋给物体的rotation从而完成旋转。

Quaternion rotationX = Quaternion.Euler(30f, 0f, 0f);
Quaternion rotationY = Quaternion.Euler(0f, 40f, 0f);
Quaternion rotationZ = Quaternion.Euler(0f, 0f, 50f);
Quaternion finalRotation = rotationZ * rotationY * rotationX;transform.rotation = finalRotation;

这个方式相较于前者在Inspector里修改不够直观方便，因此更推荐前者。